多面体polyturnon攻略
粉丝1721获赞1.8万
相关视频
 01:04查看AI文稿AI文稿
01:04查看AI文稿AI文稿家里有小月龄宝宝的,或者说是过年的时候想要送给亲戚家的小宝宝的,可以看一下 babycare 这个蜗牛爬行多面体,它现在有一个优惠券啊,就真的很划算, 主要是它这个功能真的太多了,我这两个也是他们家的,但是这两个当时好像是花了两三百,现在的话呢,这个蜗牛就它的功能,就相当于这两个玩具的功能差不多,按一下它屋顶的这按钮,它是能爬行啊,就很适合正在学爬的宝宝。上面这里呢有个小电话啊,然后这些按钮呢都是可以按出声音的,也可以切换不同的语言, 就是让宝宝去模拟这个打电话,然后他这每一面都是用小激光的,这一面的是音乐啊,他每个按钮可以切换不同的音乐,不是单一的,就只有那么几首音乐啊,他的音乐真的很多。然后这一面的就是有不同形状的小玩具,让让宝宝自己去把它套回去,这个可以锻炼宝宝的手部精细化,还有他对这些图形的认知。 然后这一面呢就是开关按钮,还有一个可以转动的东西,就也是锻炼宝宝的手部精细的。然后这面打开呢,它就是一个小镜子,我感觉这个玩具真的可以玩很久,而且它不是那种很小的,就它还蛮大的,就你这样子拎着一个礼盒去送人,我觉得也挺有面子的,也算是一个比较诚心的礼物了,而且还不是什么杂牌,是 baby 品牌。
 09:34查看AI文稿AI文稿
09:34查看AI文稿AI文稿今天呢我们来讲一下这个多面体,它叫做本边三角形多面体,它也叫做正二十面体,它是由二十个三角形的这样的面,然后组成的。然后我们看一下,分析一下这个物体,你看这个地方形成的像一个什么五边形,然后呢有五个三角形往一个尖尖的方向堆积成了一个芯体的形状, 它的轮廓呢有几条对称的一个边呢?是这条线跟这条线是平行的,这边呢跟顶边这条线是平行的。那么分析里面的形状,大家没发现,你看它每一个鼓起的地方,它都是由五个三角形组成的,比如这个地方, 这个地方你看它是一个三角形的面,这个地方这个地方它是三角形的面,你看它这样一下出现一个心形的形状,往中间顶起来,那么这个面也是一样,这边这个形状也是一样的,这个也是这样的一种感觉。 这个物体呢确实讲的人会比较少,你看它这边也是这样的感觉,所以呢它基本里面是五边形,然后顶这个尖尖这个五边形,它里面会有五个等边三角形。接下来我们来画一下,首先呢我们先定好它的一个最高点,它最高点会稍微有点斜度啊,我们在定的时候注意到这个斜度, 好通过他最高点找到这一点,我们刚才已经知道这一点跟最高点形成一个什么平行的,从前往后呢,他会带一点透视,前面宽一些,后面窄一些的感觉。这个时候我们看一下,根据他两个点,这个点,这个点,这个线的宽度和高度,我们来比较一下,看他是不是成正比,然后通过这个点连到下面这个点, 这个是辅助啊,辅助我们来完成。这个型的还是打型的, 很多人直接去切可能就没那么容易切准,因为切的比较准,但是我们借助一些方法可能会好一些。我们现在得到这一个上下的一个平行线,这个时候你知道左边的个点,右边的个点,那你这起来刚好也是什么一条平行,平行的,平行的, 而且它差不多也在中间的位置,就它的一个角度,斜度啊,看有多斜,这个就大概的先连出来,等一会可能会需要去修改和调整。 轻轻的这个时候呢,我们看一下这个点到这个点的斜度,这个斜度是处理出来的,那么这边找到,我们找到对面的对面的这个我们所谓的平衡线, 那这个你看这边的点也能找出来,那么右边的点也能找出来,这个时候我们需要去检查一下它这个边的一些长度跟斜度对不对? 这个画完呢不太准确啊。这个时候呢,我们根据你看它的外面就是六边形,外面六边形我们觉得大概接近之后,因为手绘呢没有办法做那么精准,所以说非常接近即可。 这条边我们看它的一个长度,斜度可能出了点问题,再调一下。 好,那我们紧接着来找到他这些斜边,如果有哪位可以找到这个大的,这个里面的这个五边形啊,亮面的五边形,但是我觉得找这些小斜边是会好找一点,面积小好判断。通过这个斜边我们来找到他的一条边, 然后呢再沿着这条边来到他另外的这条边,看斜度长度,好,他不在这条线上,他点在这条线的过来的位置,我先看一下这条斜度,要跟这条线要形成一个两个点点,要形成一个平行线, 那么现在我感觉它不太平行,还需要往上调整一下。 好调整之后呢,我们看到这里就得到了一条这边的边,它是斜下一点的,然后再把这个焦点连起来, 这个时候的话呢,我们再把这个边角这个小面积,把这个结构线给它连上, 好现在找到上面这个点,通过上面这条边来找了,通过这个边我们来找到这个点, 看这个斜度跟长度, 现在的话线条有点多,会有点乱,那么我们只需要把这些物体的轮廓,外轮廓、内轮廓的线条给它加重突出一下。 现在我们只需要把这个轮廓的加重体现一下它的这个形体的感觉,因为我们上面有些辅助线会干扰我们的这个观察。 这个物体的话呢,确实很少人会讲这个问题,但不太好讲这个问题确实会有点复杂。看到上面这个边,这里这个面就像一个五边形,反正就是五边形,然后有五个一二三四五五个等边三角形组成的这么一个区域。然后呢这个等边角呢会需要透视近大远小,让它视角上的一个 一个区分一个差异。你看这一块,你看一下啊,这一块区域,它其实也是刚才像我们讲这个区域的这一块区域,它也是这样的形状,朝上面这个点朝上,这个点朝右,这个点朝下,你看见没有它的这个朝向,它都是围绕一个什么五边形的一个形状来组成,这边是就像一个星星顶起来的感觉,一个星星顶起来的感觉, 你看它现在比较浅的线,都是它的一些前面打,行啊,用一些辅助线把它擦掉, 就协助我们来完成这个造型的。如果说直接去画,直接画行不行呢?很多人我看他们都直接画,也不是不行,那你要有把握, 本身就是初学者,那你直接去那样画,你判断是不准的,熟练度不够,判断不准确,是那样直接化妆呢?画不了就需要借助一些方法和技巧,因为画的本身它是很理性的,它本身是很理性的东西,在里面它并不完全理性,也不完全是感性。 好,现在呢,它整个轮廓就已经搞定了,找到影子形状,从左边转过来,它影子在右边 找影子,找影子的时候呢,你只看到这边这个顶往这边照过来啊,左上角照过来,那把它照过来,从这个角这个角照下来,光照下来到这个位置这边过来, 这个鼓点鼓起来,然后呢投下来一个影子就投影了。影子我们在这个绘画里面叫投影,还有右边啊,右边呢,这个点从这个按部的这个点投下来,投哪个位置啊? 从这个点投下来,这个位置这个影子的一个范围, 这个时候我们只需要把这个投影按部过一遍啊,轻轻的拍点线条给它过一遍,表示一下它的这个按部跟投影 稍微做点前前后前中后倾的变化就可以。 这个反光面稍微浅一点,最深的暗面就是这个右边这个面背光, 这个是个比较浅的灰色面, 因为我们画的是一个形,外面的这个轮廓线和里面的轮廓线,所以观影上没有做过多的一个处理,这是一个简单概括,这只是我知道的一些方法,如果大家有一些不一样的方法,更加容易把它画出来,也可以一起分享,一起相互学习, 这个灰面给它轻轻的过一下。 人呐,学无止境并非啥都懂,所以有东西可能它有多种方法,我只是知道分享我知道的这个部分。
42爱画画的爆炸头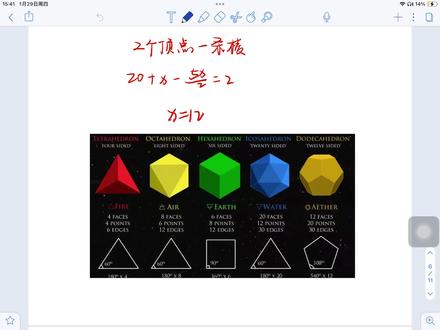 13:20查看AI文稿AI文稿
13:20查看AI文稿AI文稿所以之前也有出过一道题目,问的问题是什么呢?说请问正多面体有多少?有多少种正多面体,那这个答案就是五,是不是?所以这个图啊,考前可以多去看一看,记一记啊。可以考前多去看一看,记一记。 那么现在我们就来说一下,如果说我解决这道问题,我有两个方法,哪两个方法呢?第一个方法就是记啊,把它给记住,你是能记得住的哈,对吧?你能记得住你就记住他。那如果说我确实我没办法记那么多,那我应该重点记什么呢? 啊?重点记什么?那第一个就是你重点要记的是他什么形状就可以了,比如说我要记,呃,三, 呃,这个四面体,还有这一个八面体,还有这个二十面体,他形成的图形是 三角形,你要记这一个,要说他每个面是什么图形?是三角形,你要记住。那你其实就三个三角形吗?跟一个四边形,跟一个五边形,那我记这一个可能会相对来说简单一点点,对不对? 好,那你记重点记这三个就好了,因为这一个大家非常的熟悉,那这一个就是剩下的那一个,所以重点记这三个 啊,三角形,这三个要重点记。好,那我记住三角形有什么用呢?那现在我们就来讲一讲,我怎样用欧拉公式来去推出来,我到底有多少个面,多少个点跟多少条边,这多少个人长多少条人长这个逻辑啊? 啊?我们来看一下。首先第一个我是不是已经知道了它是一个三角形,对不对?它是一个三角形啊?相当于你知道它是个三角形之后就解决掉了一个未知数了啊?好,那么对于多面体的题型,我们重点要解决什么呢?它的重要因素是什么?第一个就是 我们先把它分开。分开?什么逻辑呢?比如说我把这个单独截出来啊? 这是一个题目,不让我们求这一个嘛?求这个二十面体嘛?正,二十面体,他有多少个?多少个?多少个顶点,对不对?有多少个顶点?好,那我们分开。分开的意思是什么?把所有的一个一个面先分开,我先剥离开来, 那么剥离开来的话,我是不是有二十个面,对吧?二十个面,我的面是有二十个面的, 这个不会改变,相当于我有二十个三角形摆在外面。好,那二十个三角形摆在外面的话,是不是意味着我的棱就有几条呢?二十个三角形是不是有六十条棱, 对不对?好,那我的顶点呢?有几个呢?那是不是也是二十乘三有六十个顶点?好,这一些是我分开之后的结果。那么分开完之后,我是不是把它给合并?第二步就是合并, 合并回去,那么我合并回去的时候,我面的数量是不会变的吧?是不是依然是二十个?这二十个面是不会变的, 但是我的人是不是会发生变化?好,那我们来感感受一下啊,我的人长这六十条,在合并回去的时候,他是怎么进行合并的? 我每一条棱在被分开的时候,我一条棱是不是左右两边各一个面?所以我的棱在分开的过程当中是被复制乘二的,那么我返回的时候,我是不是要除以二, 所以我的棱的数量是六十除以二等于三十条,也就是说我回去的时候,我棱是两条棱合并成一条棱, 对吧?少了一半啊,六十除以二有三十条,那我的点呢?点又是怎么回事呢?点就跟这一个有关了, 跟他的每一个顶点所连接的边有关。那我们观察这个图,我们是不是会发现他其实是连接了一二三四五五条边,连接了五条棱,对不对?但是我们没有记这一个啊?我们记忆的只有这一个三,是不是, 对吧?我是个三角形,只有这个三是被我记住了的,所以你发现了没?只有当你知道它是由什么图形组成的时候,你才能把它分的开。否则的话,这道题如果你没有记住,那这里是不是一个未知数? 是不是?是一个未知数啊?那现在你记住了,他就不是未知数了。好吧,好,那这一个我们没有记啊,怎么办呢?那就设未知数嘛,一个未知数我还是能解决的了。所以这里面我需要干嘛设假设每个顶点 连接几条边呢?我们连接 n 条 n 条边。好吧,每个顶点连接了 n 条边。好了,那现在我们开始顶点合并了。喔,那既然每个顶点是连接了 n 条边的,那是不是意味着我六十个顶点在往回合并的时候,是 n 个顶点汇集成了一个顶点,对吧?你自己感受一下嘛。这一个三角形的一个顶点, 这个三角形的一个顶点,这个三角形的一个顶点,这个,这个,这个对不对?我五条五条边是不是有五个顶点?那五个顶点汇集在一个顶点上,是不是五个变成了一个?那我现在就是 n 个变成了一个,那我的汇集回来的时候,我点的数量就应该是六十除以 n, 对不对?汇集合并之后,我顶点的数量就是六十除以 n。 那 你现在看一下,你合并之后的面棱和点的是都表达了, 都已经表达了,那我是不是就可以利用欧拉公式里面的点线面的数量关系去列一个方程,那就是怎么样?那就是点 加面等于零乘二,那这里面我是不是可以算出来 n 等于多少, 对吧?那我算出来 n 等于多少的时候,我再带回来去计算,那我点的数量不就求出来了吗?这也求出来? n 是 等于五的,那我点的数量是不是就是十二个? 有十二个顶点,那这道题我是不是做完了?这里面是只有一个未知数?记住,但是你需要去记住,就是它是个三角形,三角形这个是你得要去记的,那你们可以也去试试看。如果说 我不知道他是个三角形呢?我也记不住是个三角形呢?那怎么办?那就再来一个未知数吗?那就变成了两个未知数,是不是?那两个未知数?如果我能有两个方程,我也可以解,但是很明显你其实只有一个方程,就是欧拉公式,那就变成了两个未知数。一条方程我们叫做什么? 不?呃,那个叫做不定方程,对不对?那不定方程我要去解。这道题也很好解,为什么?因为这里面的未知数,我们设了个 n, 再设一个 m 的 话, n 跟 m 它都是整数,那整数的不定方程, 那太好解了,是不是?太好解了?你可以去解解看,那就说你可以再设一个量,叫做什么?设, 设,设这个二十面体,正二十面体的每个面,每个面 为,为什么呢?为 a 边形,对吧?为 a 边形,那你是不是多了一个未知数 a, 那 你这也就是二十 a, 这里也是二十 a, 是 不是?那这也就是二十 a 除以二, 那这也就是二十 a 除以 n, 对 吧?那就变成了两个未知数,两个未知数不定方程, 而且是整数的不定方程,你可以用凑成大法去做,对吧?好了,那这就是啊,第一类,第一类题型啊,就这一种,分开合并这样子来去做,这是正多面体的。 那第二类题型呢?就是这一种,那这一种啊,首先题目你先读清楚了,对吧?题目读完之后,你看这道题,他就已经告诉我们这个关系了,题目已经给了我们这个关系了,我是不是不需要自己去记了?但是你还是要记啊,谁知道题目到时候给不给呢?是不是? 好,那这里面他啊,说了一些关系,他说这里面呢,是均由正五边形和正六边形组成的,所以他不是正多面体了吧?他就是一个多面体,只不过这个多面体呢,他是由五边形和六边形去组成的。 好,那现在他就给我们举了个例子吗?是不是?那现在让我们去求什么呢?他说这样子的一个多面体有这么多种,他让我们求这一个八十四,这一个的 结构的正六边形的个数为多少?那八十四有什么特点?这个八十四是不是?你看我的六十,那就是有六十个顶点,那也就意味着我这个八十四,比如说这个正多面体,我是不是已经知道它是有八十四个顶点的? 这个是已经合并了的状态啊?合并的状态它是不是有八十四个 顶点?顶点是有八十四个的好,剩下东西一起都不知道,对不对?什么都不知道,没了好了,但是现在我们有一件事情是知道的,记住,解决多面题很重要的一个东西是什么?两个啊。第一个是由什么组成? 由什么组成?题目是不是已经告诉我们啦?就跟那个三边形、三角形一样,这也是五边形跟六边形,对不对?那你就说它这一面应该由 x 个五边形,我不知道几个,那就 x 个吗?和 y 个六边形组成, 至少我知道他长什么形状,那这也是两个未知数。 x 个五边形和 y 个六边形,我是不是可以分的开?分开,分开了之后对不对?这一个事情就决定了,你可以分开。那我分开之后我的什么呀?我的面有几个呢?面的数量是不会变的,是不是 x 加 y 个, 那么我的顶点的数量就应该是五 x 加六 y 啊?这个是分开的状态。那分开完了之后我们是不是要合并?那合并其实很简单,合并之后我的面还是不会变的。我的顶点呢? 顶点我有两个表达题目已经告诉了我有八十四个了,对不对?那我同时我也可以怎么表达我的顶点?合并由什么决定?是不是由他的每一个顶点连接了几条人决定?那这个图给了我们呢? 这个图给了我们,我们是不是可以观察得到每一个顶点是由三条连接的三条棱,所以是三个顶点合并成了一个顶点,所以我这一个八十四个顶点是可以通过五 x 加六 y 除以三得来的。 三个顶点汇集成一个顶点,你看第一个方程是不是有了,对吧?好,接下来就是我们的棱棱就最简单啦,他是不是两条棱合并成一条棱?因为你在分开的时候一条棱当两条棱用嘛,所以我的棱就是五 x 加六 y 除以二, 那是不是分开合并搞定?那现在我们来看一下我们有几个方程,我有两个未知数,第一个方程是不是这一个八十四等于什么什么什么的?第二个方程是什么?第二个方程在这,对吧?点线面的关系,那也就说我的面 加上我的顶点八十四是不是等于人长的数量加二, 那这是我们的第一个方程,这是我们的第二个方程,两个未知数。两个方程,那我是不是直接解二元一次方程就可以了?我就可以抽出我的 x, 也可以抽出我的 y, 那 题目问的是正六边形的个数,那不就是 y 吗?那就做完了对不对好了。所以这个,嗯,多面体的这种题型, 两个很关键。第一个有什么组成,你就说他,他有什么图形组成?你是全都是三角形啊?还是说有五的,有六的呀?那你要把它给搞清楚是由什么组成的,那么那需要设未知数,你就去设。 第二个就是你在合并的过程当中,合并的过程当中是由顶点连接了几条棱 来去合并的,对不对?因为线楞长的合并很简单,但是顶点的合合并是需要知道条件的,知道吧,也就说每个顶点连接了几条楞,这个动作很重,这个这个这个条件非常的重要。 好,那这一个就是欧拉多面体的一些题型,那大家可以把这两类题型去,第一个是这一类题型,对吧?你们可以去把它给 啊手练一下。然后这个图呢,也建议去多记一记啊,多去记一记。好吧,那祝大家二月一号考试顺利啊。
7🍑小Y 07:19查看AI文稿AI文稿
07:19查看AI文稿AI文稿hello, 大家好,今天呢给大家讲一个呃几何叫做欧拉多面体,多面体的这种题型啊,像这一种题型的话呢,近几年的竞赛里面其实都有考到 那有学过的同学或者说有进行过记忆的同学的话,那这类题目对他们来说其实很快就可以做出来,并不难啊,因为他通常来说是个填空题是不是?好,那如果说没有学过的同学不了解的话,那这道题你要去做其实还是挺难的,因为你, 嗯他不是我们常规的那一种说呃平面几何或者说我们常认识的什么圆锥、圆柱和长方体这一种类型,他不一样,他是一个多面体,就是说我们的八面体啊,十二面体啊,十八面体啊,那这种在我们的呃, 他不是我们接触,不是我们常接触的那一种立体图形了,所以呢,如果说我出出现了一种我不认识的立体图形啊,二十面体,让我去想象他长一个什么样,其实我是没有办法去想象的, 对不对?很难想象,想象不出来啊。所以像这类题目的话,就是你要去知道他有什么呃公式以及他的公式证明是怎么样子的,以及我要怎样运用公式去解决这一类题目啊,他都是有有方法的。 好吧,那首先第一个就是我们先认识一下多面体公式,欧拉公式到底是一个什么东西?那几何我们知道无非研究的就是点线面嘛,对不对?点线面,所以 欧拉公式它其实研究的就是点线还有面之间的关系,它的关系是什么呢?就是点的数量加上面的数量等于人长的数量加二,比如说拿一个我们最熟悉的长方体来说, 我长方体是不是有八个顶点?我的面是不是有六个面?我的人长是不是有十二条?那你看八加六是不是等于十二加二,对吧?这一个就是欧拉公式,欧拉多面体的一个公式啊。那不管, 是啊,四面体啦,正八面体啦,正十二面体啦,他都是这一个,那这就是我刚才说的正十二,正,我刚才说是正二十,对不对?那正十二面啊,正十二面体,他是这样子的。 好,那么我们的证明呢?第一个证明是有一个叫做投影法的,我觉得是相对来说,呃,可以去 理解,能够去呃,理解得到,但是你需要花时间慢慢去看,慢慢去理解。这里我不会过多的去陈述这一个证明是怎么来的,因为这一个其实还是有一点难度的啊,他是往后面高中的时候也会去 啊,高中到竞赛这一个板块会用到的一个方法,你可以去做这一个证明,你可以慢慢去了解啊。好,那我今天的目的主要是什么呢?是为让大,让大家快速去 掌握这一个知识,因为不是马上就要跨北考试了吗?对不对?马上就要跨北考试,二月一号,所以呢,大家可以去掌握一个方法, 那这一个方法其实是为了让大家更能够快速的去记忆啊,你可以这样找规律,那找规律的话呢?是我们小学常用的,那如果说我再往后面要严谨一点,其实我应该是叫做数学规划法,对不对?数学规划法。好, 那我们就以长方体这个来说,你去记忆,其实这一个公式你是可以很快去记住的,对吧?就点线面之间的关系嘛, 那这一个就是数学规划法,我从假设 k 多面体符合,到 k 加 e 多面体仍然符合,那这个事情我就是成立的。好吧,那这一些证明呢,大家可以去花时间啊,自己去慢慢的去理解,去了解,因为你先还是需要借助到很多一些啊。视频, 你要从了解立体几何这一个方向去入手的。那我们今天呢,主要就是告诉大家,我基于这一个公式,我怎么 解决问题。因为知道公式是公式,但是实际上在题目的运用当中,他并不是说只有公式就可以了的。好吧,那我们来看两种题型啊, 这是第一种题型,他直接问我们正二十面体有几个零点,那你想想看,这是一道填空题,那如果说 我在考之前,我就已经知道这几个多面体本来就不多,正多面体总共就才五个, 那如果我记住了那道题,是不是我直接十二就可以往上填了,对吧?好,所以说考前啊,大家可以多看看这幅图,对不对?多看看这幅图,记一记是不是临时记忆,先记住,一旦考到了的话,那么这一个你是可以快速去解决问题的。 ok, 好, 那我们来先来这里面可以给大家讲一下,为什么这么多面体就只有这几个图形。 这个是正四面体、正八面体、正六面体、正二十面体和正十二面体,我就只有这几个,那我们会发现他的正多面体,这是正三角形, 正三角形,正三角形是不是只有三个,对吧?正四边形,正五边形啊,没有正六,没有正七,也没有正八,为什么呢?是不是?那我们来想象一下看啊。如果我是一个多面体的话,立体多面体, 首先我是不是一个?我得要有三个面组成才可以吧?如果我只有两个面,我是没有办法,我是说一个维度上就是这一圈或者这一个,比如说一个顶点,以某一个顶点为例,我这一个顶点是不是至少是要连接有三个面才可以的? 如果我只连接了两个面的话,我左边一个,右边一个,其实我是没有办法形成一个立体图形的, 所以一定要有啊,三个面至少要有三个面,然后往上走嘛,对不对?那就是四、四、五、六七八这样子往上走,那我是不是从三个面 围成一圈开始去去入手去判断呢?那你看我是六十度的角,三角形是六十度的角,我是不是至少要有三个 围成一圈,那就是这一圈吗?那这也是一百八十度,四个的时候就是二百四十度,五个的时候就是三百度,六个的时候就是三百六十度了,那三百六十度就出问题了,为什么呢?三百六十度它就变成了一个什么面了,它就变成了一个平面的概念了, 是不是相当于是你围完之后,你最后一个一进来一拍,他就变成了一个平面,他并不是一个立体的一个图形,所以正三正多面体以三角形组成的话,只有折 三个,只有这三个,那就是一、二、三。那你想想,看到这个九十度的就很好理解了。九十度那我是只能乘,我至少要三个,那是不是九十乘三?那就是二百七乘四,我就三百六了,又变成了平面了,是不是?不可以? 如果你比三百六还大,那就变成一个凹进去,那也不合理吧?是不是?好,所以他就只有一个,那接下来就是到五边形了,那五边形的内角和你是不是也可以重,对吧?那六边形为什么不符合呢?那肯定是因为六边形的 内角,六边形的一个内角我乘三就已经大于三百六十度了,所以就不可能。那再往上走就肯定就是都没了,都没了,好吧?
5🍑小Y 16:49查看AI文稿AI文稿
16:49查看AI文稿AI文稿今天我们就主要来研究多面体,大家来给多面体能否下一个定义?好,有没有同学来说一下?杨丽涵 有许多个平面拼凑在一起组成的一个几何,许多个平面拼凑在一起组成的几何体。好,请坐。他的这个说法我们把它再完善一下,应该是由 若干个平面多边形围成的几何体,就把它叫做多面体,那么多面体的各个部分也有对应的名称,围成多面体的各个多边形叫做多面体的面, 相邻两个面的公共边叫做多面体的棱,棱与棱的公共点就把它叫做多面体的顶点。那接下来我们就来研究几类特殊的多面体。首先来看一下棱柱,那请大家来观察一下下面一些几何体,哪些是棱柱呢?一 一二三二。好,那观察一下你选出的这些棱柱,你能归纳一下棱柱的结构特征吗? 主要从哪些角度去描述棱柱的结构特征呢?请大家思考一下,小组讨论一下。好,有没有同学来跟我们分享一下你发现的棱柱的结构特征。周身头顶面和底面是平行,各个面都是平行,四边形 侧棱都相等。好,请坐。那还有同学补充吗?补充,一侧公平面,间侧面公共边,他都是平行, 很好,侧面公共边都是平行的。好,那么我们来思考一下,如果要描述棱柱的结构特征的话,其实我们应该从哪些角度去进行描述会比较准确一些?棱柱是多面体,组成多面体的是 这个面是吧?那从面的形状和面与面之间的关系进行描述, 我们首先可以发现棱柱的里面是平行的,有两个面互相平行,并且其他的各个面都是什么形状,都是四边形。嗯,好,在者 这些相邻的四边形,他们的公共边互相平行。大家注意,这里两个边指的是棱柱的底面,这里四边形做的强调,它其实指的是同一对象都是棱柱的侧面。好,那这样我们就给出了棱柱的定义, 一般的有两个面互相平行,其余个面都是 四边形,并且相邻两四边形,它的公共边互相平行。好,我们把满足这三个条件的东边体把它叫做楞柱,楞柱的各个部分也有对应的名称, 这两个面叫做棱柱的底面,对底面,这个叫棱侧。清楚,侧面,侧面,侧面,这个是棱对,统一称为棱,那这个就是侧棱, 这个点叫做棱柱的底点。好,棱柱的各个部分的名称我们知道了,接下来我们来分析一下,我们在对棱柱下定义的时候, 这几个方面主要是从棱柱的哪些部分去下的。定好,第一个两个面互相平行,指的是他的底面对住的底面, 其余各面都是四边形,指的是侧面相邻两四边形,公共边是这个棱柱的侧棱是侧棱,那么我们在表示棱柱的时候,使用的是它的两个底面进行表示,中间用一个杠号做连接。 那接下来请大家来动手做一下以下的说法是否正确,如果不正确,请同学们在导学案上画出觉得的反例。 好,小组之间可以互相讨论一下,分享一下你们的结果啊。好,请两个代表来分享一下你们的结果。第一题用同学来说一下 李金星,第一个可以是轮胎,你先说是对的还是错的?错的,反立式轮胎非常好,请坐。轮胎确实是满足两个面孔相平行,其余都是四边形,但显然不是棱柱,是吧?那第二个大家觉得对还是错啊?错, 有没有同学来分享一下?我把一个棱柱折一下,大家能想象到这个惊心吗?能想到请坐 这么一个几何体是吧?好好,大家来看一下,他,这显然不是棱柱。那我们从另一个角度去分析一下,这里有两个四边形的面,他们的公共边是 这条边,这里又有两个四边形,它公共边是这条边,这两条边不平行,对或不平行,所以它不是棱柱。那如果我要使它成为一个棱柱,那就要对它做一个什么处理呢?就是一个折了一下的棱柱,是不是只要把它掰直就可以了?好, 那大家来思考一下,现在要对棱柱进行分类,可以从哪些角度去分类?看一下这三个棱柱,它的底面 多边形的形状是不同的,所以我们首先可以按照底面的边数进行分类,分为 四棱柱和五棱柱等等。对于四棱柱来说,如果底面是一个平行四边形的四棱柱,我们又把它叫做平行六面体,其中长方体和正方体都是平行六面体。 那么除此之外,大家想一想,还可以从什么角度对棱柱进行分类呢?这里这三个图还有什么区别没有 斜的,还有直的,所以我们可以按照侧棱与底面的位置关系去分类。如果侧棱他不垂直于底面,我们就把这个棱柱叫做 什么?楞柱?斜楞柱?对,如果垂直底面,那就叫做直楞柱,直楞柱当中如果底面是正多边形的话,我们又叫做正楞柱,如果不是,那就叫其他直楞柱。 很好,好,下面我们来研究第二类特殊的多面体轮锥。现在老师手上有一个轮锥的模型,我想请一个同学上来用这个模型向大家去介绍一下,你发现的轮锥的结构特征是什么?有没有同学来 描述一下?刘文哲,他是底面为多边形,其余个面对三角形且共顶点的那个体。什么体?多面体是吧?好, 大家觉得他的描述怎么样?还有没有什么要补充的?有没有同学把他的描述可以再改进一下?好,他 描述的很好,请坐。他。其实刚才讲到了一个,我们可以类比前面棱柱的描述,我们是从棱柱描述的时候,是从面的形状和面与面之间的关系去做描述的。他当时他在描述棱柱的时候,他也讲到了 里面是一个多边形,侧面都是三角形,这是从面的形状上来分析的。那面与面的关系,这些三角形有个什么特点呀?这些三角形有一个公共点,是不是?所以我们对棱锥的描述,第一 要求棱锥有一个面是多边形,第二要求其余个面是有一个公共顶点的三角形。我们把满足这样的条件的多面体叫做棱锥。好,这样我们就给出棱锥的定义,有一个面是 多边形,其余个面是有一个公共顶点的三角形,那能追的各个部分也有对应的名称,这个面把它叫做能追的什么面面, 这个是轮锥的侧面,这个是他的侧呢?这个点是轮锥的对顶点好,在表达轮锥的时候,我们用顶点和底面进行表达,中间用一个杠号连接 好。接下来请同学们来做一下这道题,以下说法是否正确?如果不正确,大家还是在导学案上将对应的反例发出来,导致这里有两种模型,有没有同学 也用这两种模型来试着拼接一下,看能不能找到反例?还有其他同学自己动手画 好,可以和同桌身边的同学去分享一下。好,我们请两组同学来跟大家展示一下。好,第一个,哪一组同学愿意好一个一。先跟大家说一说对不对?法令是什么?这个不对,不对,你找到法令吗? 反义是这样子的,这个个面都是有一个面都是,那反正这个满不满足第一位的条件,这样子,这样子,这是一个一个面是一个面是多边形,一个面都是三角形。 这个几何体大家发现没有,他是有一个面是,这个面是多边形,其余各面都是三角形,但显然不是轮锥,他不满足什么?他不满足第二个侧面的三角形有一个公共的顶点,其实你刚才做的那个也是第一问的一个反例, 大家看一下这个,显然他也不是一个轮锥,是不?他也满足有一个面是多边形,这里我们三角形面是不是也是属于多边形?他也是第一问的法力啊,很好,第二问,有没有同学来说一下来就 张天赐, ok, 首先啊,让我们看这个形状,这个是一个面,他是一个三角形, 这里也是,这里一个面是三角形,这里一个面也是三角形,这里也是,这个也是,这两个也是三角形,数一下,他总共有六个三角形。好, 这个其实就是我们刚才那个例子。哎,对,他也是满足各个面都是三角形好,请他也是满足各个面,但是不是轮锥是吧?对,好,下面请大家来看一下这两个几何体是否是轮锥。第一个是的, 他是一个几轮转转好,第二个是不是不是他们满足他们满足三角形交于侧面都是三角形,且交于同一点转。好,接下来我们对轮锥进行分类,可以类比前面轮珠的分类方式。首先我们可以从哪些 方面对轮锥做分类?轮锥的里面的多边形边数是不同的,是吧?所以首先我们可以根据里面多边形边的个数分为, 这是三轮锥、四轮锥和五轮锥。其中三轮锥是面数最少的轮锥,它一共有几个面?四个面,我们又把它叫做四面体。好, 那么除此之外还有没有其他的角度对准对准等嘞?我们首先看到是底面多边形边,那底面有没有特殊的形状呢? 正多边是正多边形,对,如果底面是正多边形,并且它满足顶点到底面中心的连线 垂直于底面,这样的轮锥就把它叫做正的锥。好,接下来我们来看第三类特殊的多面体轮胎, 请大家来观看一下这个轮胎的形成过程,然后用文字语言把它描述出来。好,我们有没有同学来说一下你刚才看到的这个过程?陈奇涛,用一个 平行于底面的一个平面聚集平行于轮锥的底面的平面聚集轮锥,得到 下面那个东西就是轮胎,它这个说的是比较准确,非常好清楚,那我们可以把它变得更加的规范,我们来看这个过程应该是一个怎样的平面, 平行于平面的平面去截轮锥,截得的 一共有两个部分,我们取的是下面的部分,那描述就是用前面与里面之间的那部分叫做轮胎,那这其实说明轮胎它是由轮锥进行一个什么做 切割,更准确的描述应该是截取得到的。好,那下面我们就来看看轮胎各部分的名称, 这两个面,这个面是轮胎的什么?上底面,这个是他的下底面,哎,这个是侧侧面, 这条边侧轮,这个点是点点好表示轮胎,我们就用上底面和下底面进行表示,中间用杠号做连接。 好,下面请大家来思考一下下列的几何体是否为棱台,在你们的导学案上去做一下,可以跟同学们去讨论一下。好,我还是请两个同学来分享一下你的结果没有?同学来说一下。刘向北,你可以上来 大家来讲解一下。轮胎他是由轮锥结起来成的,所以他的侧轮延长之后应该会交于一个顶点,但是这一个他是没有交于一个同一个点的, 所以他不是轮胎。那其实说明我们轮胎的侧轮他需要交一点,延长之后要交一点,这样才能是由一个轮锥进去得到的。好 啊,第二个领军,因为轮胎是由一个平行于平面的平面截取而成的,但是可以很清楚看出上平面,上平面和下平面他是不平行的,所以他不是轮胎,你们点一下看,但是 他的侧轮先交还是一个平面,但是还是不是一个轮胎?说的好不好?好,他这里为什么不是轮胎?是因为他虽然是由轮锥结得的,但是不是一个平行于底面的平面结出来的。好 啊,根据这个题目和我们前面对轮胎的定义,大家来分析一下轮胎应该是具有哪些特殊的性质,同学来说一下吧, 你觉得轮胎有哪些性质?我们一条一条来补充。欧阳志奇,上底面和下底面是平行的,下底面是平行的,还有什么特点没有?上下底面除了平行之外两个相似,对,上下底面是平行且相似的多边形。很好,请坐,还有没有吭声? 侧轮延长后交汇点。对,刚才那道题,我们看到侧轮延长后交汇点,那么侧面都是梯形。好,非常好,请坐。 那,其实我们可以发现我们轮盘的性质也是从里面侧面和侧轮去进行分析的,跟我们轮住的定义是不是不谋合?好, 那么我们还是来对轮胎做一个分类。那大家来想一想,可以从哪些角度对轮胎做分类?可以跟同学们去 讨论一下。好来看一下轮胎的分类。首先我们从什么角度去分底面?对,跟前面是一样的是吧?根据底面多边形边的数目分为 三轮台、四轮台和五轮台。那除此之外还有什么角度没有?对,我听到有人说底面的什么特殊 形状,如果底面是正多边形,也就意味着这个轮胎是由正能锥截取得到,那像这样的轮胎就把它叫做正轮胎。
13数学在线 04:34查看AI文稿AI文稿
04:34查看AI文稿AI文稿一个性价比极高的玩具,非常锻炼宝宝的专注力,还有手眼协调能力,并且它打底能玩到两岁,因为它每一个面的难度都是根据宝宝的月龄来逐渐增加的,比如刚开始小的时候就玩点简单的,来回挪一挪,或者这种简单的操作就能让它动起来,小朋友就很感兴趣。 再大一点,再逐渐增加难度,像这种有联动的以及需要小手指去摁的,再长大一些可以玩这种旋转的。像我家现在这个年龄就特别爱玩这种,把它对进去,然后再拿出来,它每一个还可以单独拆下来,如果前期宝宝比较小的话, 就给他拿下来玩,也可以带到包里边拿出去。一共二十二个面,每一个都可以拆卸,六个多月会做了能自己抱着玩的,就这样整个去玩,玩法就非常多样,我当时买回来自己还玩了半天,并且价格还很便宜,正常买一个六面体都得一百多了,这个二十二面体只要这个价格,孩子一玩玩半天你也不用管他啊,还锻炼专注力,所以没准备的姐妹可以准备这一个,特别划算。
1时光超市 01:37查看AI文稿AI文稿
01:37查看AI文稿AI文稿宝宝,然后这个里面的话可以拆分成,然后可以拆分成这种手摇铃,手摇铃哦,可以让宝宝 可以这个里面三十多种玩法于一身的,然后手摇铃都不用再单独买了,因为你们家五个月宝宝正在属于口育期对不对? 爱啃爱咬呀,拿什么吃什么,这个可以当一个小牙胶来用,可以拿到手里可以练习抓握,喜欢扣眼睛的,扣鼻子的,让宝宝的小手去扣,去锻炼手指精细动作。还可以当小牙胶来用,小手去拨去转,然后有摇铃的声音,可以发出声音的玩法真的超级多 哎,这是什么呀? bb 器对不对?然后妈妈拉这头,宝宝拉这头,我们两个去拉一拉,去扯一扯,会发出声音,他的小嘴巴,小小耳朵全部都是软牙胶的啊。宝宝,然后这个这个大白鹅,大白鹅,人家设计是不是非常合理,你就拿到手里,这样去摇一摇,也是可以发出声音的, 还可以玩塞塞乐,可以锻炼宝宝的抓握能力,教宝宝来拿出来,塞进去,教宝宝来做空间的感知能力,是不可以五个月以上,我们去体检, 耳保医生就会检查宝宝的抓握能力,会给他一个东西,让他去抓这个玩具就可以让宝宝反复的拿出来,塞进去,拿出来,塞进去,推荐买这个宝宝,这个玩法更多, 玩法会更多,而且采用全部都是加厚的 abs 环保材质,让宝宝随便啃咬,没有一点点问题。里面是三十多种玩法于一身的宝宝,我们还可以当一个引导型玩具,然后这样滚着去跑,引导宝宝去爬行,是不是也可以让宝宝去爬行?是不是也可以?
 02:51查看AI文稿AI文稿
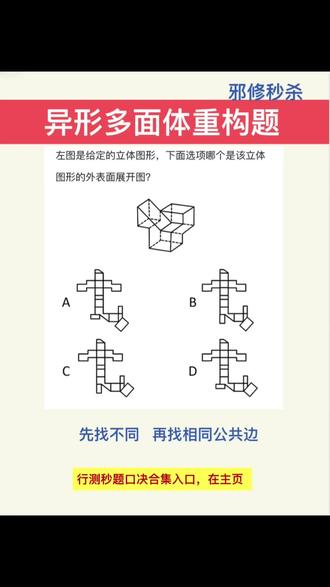
02:51查看AI文稿AI文稿异形多面体重构这个题,今天带给大家一个斜角秒杀的一个小方法,让我们以后再遇见这种题,再也不用担心,不用害怕, 没有任何的空间想象能力,我们也是可以做出来的。这里给大家放了一个小技巧,这个技巧叫做先找不同,再找公共边。用这个方法,我们在考场上能够快速的秒这种题,而且能够保证一定的正确率。那么具体应该怎么做呢?给大家放了一道题,然后我们先练习一下啊。首先第一步,你看他说先找不同, 然后再找公共边,那不同怎么找呢?我们来看一下 a、 b、 c、 d 这四个选项,它哪里有不同?我们看一下 a 选项的这个地方和 d 选项这是不是一样的?然后这个 b 的 这和 c 的 这是一样的,对吗?那我们就可以俩俩分组,你看 b 和 c 是 一组, a 和 d 它属于是一组, 那么我们就应该进行第二步了,我们要找公共边,那公共边怎么来找?我们拿 a 选项这个为例啊,我们来看一下,比如说这个地方和这个地方,它俩是不是应该属于一条公共边, 但是他俩是一长一短,所以就不可以,这个选项肯定是不可以,那 a 不 可以,那我们刚才说了, a 和 d 他 俩是捆绑的, d 肯定这个地方也是错的,对吗? 那我们来看一下 b 和 c, b 和 c 的 公共边怎么找?你看一下我们这个地方是不是他们俩是公共边,是等长的,他们俩也是等长的?那继续我们再来找,我们来看一下这个边,这条边和这条边,他们俩等长的,我们来看一下 c 这条边,还有这条边是不是等长的, 所以我们这道题就选择到了 c 选项,然后我们再来练习一道题,我们来看一下这道题啊,我们也是按照刚才的那种方法来做,先找不同,我们观察一下 a、 b、 c、 d 选项哪里不同,是不是这个长方形的方向不太一样,对吗? a 和 c 选项全都是在一边的,然后 b 和 d 选项是一左一右的,一上一下的这种是不是?那我们思考一下,非常简单,他俩如果要是在一起,能拼成这个图形吗?是不可以,他肯定是一上一下的才能拼到一起,对不对? 所以这个时候我们就可以 a、 c 捆绑全干掉了。然后我们来看一下 b 和 d, 我 们来找一下公共边最简单的一个地方,我们来看一下这条边是 是不是特别长,然后这条边特别短,所以这个选项肯定就是不行的 d 选项,然后我们验证一下 b 选项啊,你看这条边还有这条边是不是等长的,对不对?然后我们这条边和这条边也是等长的,所以我们这道题是选择的二 b 选项啊,像这种题,真的我们把这个口诀记住了,主要是找这个公共边啊, 把它记住了之后,我们这道题是很快很快能秒杀掉的,而且能给我们节省很多的时间。像这种行测秒推的口诀,这个合集我已经放在主页这个入口了,大家有需要的话可以自行去领取一下的秒题口诀。我们总结了一百多个,一到两个视频肯定是讲不完的,所以给大家总结了一套四天八小时的考官级顶级技巧课, 针对今年的最新国考改革后的考点,最新题型后的秒杀逻辑,这些技巧对应的题型我也会汇总到 ai 公考库学习,大家评论区见。
42韩优米 04:43查看AI文稿AI文稿
04:43查看AI文稿AI文稿一个性价比极高的玩具,非常锻炼宝宝的专注力,还有手眼协调能力,并且他打底能玩到两岁,因为他每一个面的难度都是根据宝宝的月龄来逐渐增加的,比如刚开始小的时候就玩点简单的来回挪一挪,或者这种简单的操作就能让他动起来,小朋友就很感兴趣。 再大一点,再逐渐增加难度,像这种有联动的,以及需要小手指去摁的,再长大一些可以玩这种旋转的。像我家现在这个年龄就特别爱玩这种,把它对进去,然后再拿出来,对进去,再拿出来,他每一个还可以单独拆下来,如果前期宝宝比较小的话, 拿下来玩也可以带到包里边拿出去,一共二十二个面,每一个都可以拆卸,六个多月会做了呢,自己抱着玩的,就这样整个去玩,玩法就非常多样,我当时买回来自己还玩了半天,并且价格还很便宜,正常买一个六面体都得一百多了,这个二十二面体只要这个价格,孩子一玩玩半天你也不用管它啊,还锻炼专注力,所以没准备的姐妹可以准备这一个,特别划算。
 17:07查看AI文稿AI文稿
17:07查看AI文稿AI文稿好,那我们来看一下这道题吧。呃,这道题呢就是欧拉多面体公式啊,呃,这个简介,这个题干大家也看完了啊,也看完了,也就是这个猜想大家也看到了,就是有这样的思考,这样的正多面体到底有多少个呢?所以讲这道题之前,我们也可以先看一个视频吧,那也可以看个视频啊,带大家科普了解一下这个欧拉多面体公式啊,这个视频,大家看一下欧拉公式。 好,那么到这我们先来暂停一下,来看一下啊,这个欧拉多媒体公式先研究的是一维的,是一个平面的,一个平面呢,你看这上面不是有很多点吗?对不对?他就研究了从最简单的开始,哎,这个点数,还有这个棱数,还有这个面数呢,他研究了无数个东西之后,发现横成立这个式子, 也就是什么呢?这个顶点数减去棱数加上面数呢,是很等于一的啊,然后我们从面,我们整个这个空间是不是还有立体的图形呢?对不对?所以他继续开始研究啊,哎,到底是多少钱啊? 二号, 好,到这我们来看一下啊,呃,也就是说,呃,几个几个立体图形啊,但是我们常规考的主要是考第二个啊, 如果对于这个多面体来说,就是立体图形,凸多边形,凸多面体,那么他都满足这个数呢?等于几?等于二,这个公式大家看懂了,是不是就是有满足一个什么加什么减什么的形式,对不对?等会详细给大家介绍啊。如果平面的话,这个数呢就是一,如果是多面体的话就是二,如果是挖空了,就像一个甜甜圈一样的话,它就变成零了。 朋友们啊,那么了解这个之后呢,我们再回到我们这道题目上来看一下啊,这道题目上来看,哎,也就是他在参观的时候,他也发现了啊,第一步,哎,这个黄铁矿的晶体,化学上当然学了,这个黄铁矿是不是, 哎,那么当然,为什么不用他来练习呢?因为这个东西有污染,有油啊,是不是,哎,不太好,是不是?我们正常用什么磁铁矿啊,这些的,是不是,哎,用这些来也练啊?好,那么来看他呢,这个书上也给了,但是化学书上也给了这个黄铁矿,他的晶体都是,哎,标准的这个正方体, 有看过书上那个姐姐吧,是不是,哎,而且黄色的啊,还挺好看的,是不是啊?有点像黄金的感觉,但它不是黄金,是不是?好,那我们来看它全是正方体,好,那么就会想,哎, 假如说每个顶点,我们来看这个正方体,每个顶点发出的都是连了三条纹啊,都是三条纹啊,查找资料后发现,这种各个面都是全等的正 n 边形,注意了啊,每个面都一样,而且都是正的 n 边形,你比如像正方体每个面是不是正四边形,是不是啊? 然后呢,每个顶点连接的,注意这个 r 有 要求, r 呢,是大于哪三条的时候,这个立体图形呢?叫正多面体,好不好理解哎,他其实说换一个更白话文的一句话就说,每个面是不是都是正多边形? 朋友们,哎,这样的一个形式叫正多面体啊,好,那么下面给了几个例子。第一个,哎,但是他思考了,他说,请问这样的正多面体到底有几个呢? 在引入这个之前呢,给了很多个字母啊,给了很多字母,因为这个公式里要涉及到这个东西的。那么第一个量啊,每一个面假如说是 n 边形,这个好理解吧,我们正常也是 n 边形,这样来衡量是不是好?那么第二有 v 的 顶点,大家刚看视频也知道了,这个 v 呢,当然有个英文字母了,是不是它的名词是 vertex, 但是他一呃这个名词的话,就是他的个数的话,就是 v, e r t, s, e, s, 是 不是?你也可以顺便记个英文单词来,万一考到了,对吧,这些英对吧?说这个网红获得这个奖了啊,他研究什么什么各种东西,万一就突然引入这个英文单词了,是不是?然后第一问,阅读理解啊,请问这个单词的含义,你觉得它的意思是什么? a, b, c, d, 是不是哎,万一呢?是不是哎这个东西呢?因为这个欧拉这个公式非常有名啊,是你能背会的更好了,就像你背面积公式一样的派儿方是不是?那这个公式你将来还是要背对不对好。所以这个 v 指的是顶点个数的,它的首字母缩写啊,首字母缩写 好,这个 e 呢,大家也看到了, e, d, g, e 是 不是? i 指是不是啊?那么这个单词呢,就是楞的意思,楞的意思啊,然后呢,每个顶点发出呢,都接了 r 条楞,然后呢面应该知道 face 吗?脸面,是不是啊?哎,一共有 f 个面好,那么他做了观察之后,列出了这个表,我们来看一下这个表格 啊,看给了一个表格,刚应该有看出来那个表格的形式,什么加什么减什么,记得吧,是不是?哎,所以这块如果你能知道这个公式,你能背会的话,那这题更方便了。这个公式永远都是 v 加 f 减 e 等于二, 这公式必须给我背会,如果真考的话,要知道知道吧,这个就是欧拉多面体功,这个公式非常有名啊,这是非常有名,就将来研究破腹学也好或者什么的。哎,万一在座的各位将来成为一个数学家了呢,或者研究数学领域了呢?是不是觉得是数学专业呢?你要学破腹学呀,是不是这个东西得知道呀?哎, v 加 f 减一等于二,注意是减的是冷场。 v 是 顶点数啊, f 是 面数, e 呢是棱长数啊,棱数啊,永远等于二。立体图形啊,立体图形。好,那么来看一下啊,那么这个公式大部分同学记这个呢,只记这个公式,那你做题就可能就是有局限性了,我们正常做题,你有没有发现题盖上还有两个星星没有使用的,一个是 n, 还有一个是 r, 回一下刚,这个 n 指的什么?是每个面是几边形,是不是这个 r 是 每个顶点,是发出了几条棱,怎么着?是不是还都跟这个棱有点关系? 你看每个面是几边形,是不是涉及到是几条棱,每个顶点发出几条线,是不是也是棱,对不对?看来这两个量是不是都是为了来求这个一,这个棱啊,对不对啊?所以我们报这个猜想来看一下,会发现存在一定的关系。第一个, 呃,从这个面的角度出发啊,你看,小明进一步开始研究了,以正方体为例,那么他有六个面搭上了,他有六个面,我们把这个正方可以挂在旁边啊,来看一下,分析一下啊。 好,那么六个面每个面都有四条边,那这个六个面的边数之合是不是应该是六乘四?是不是应该等于二十四?但是你想想看,正方他本身只有几条棱, 上面四个数是四个,下面是不是也四个?是不是一共只有十二个?那为什么我算起来是二十四,他那个却是十二呢?那么来观察一下,这里头每一个来这个面跟这个面是不是共用了一次,是不是被重复计算一次,听懂了吧?对不对啊?每一条棱大家发现是不是都被重复了一次, 听懂意思了啊?你看这个面跟旁边这个面,哎,这个用了一下,就这个面跟他每一条棱是不是都被重复了一次,所以需要除以二,哎,我们就计算出来了啊,所以从二四到十二是需要除以二,由此我们就得到了一个公式啊,得到一公式,正 f 面体的棱数应该怎么算呢? 他来想了啊,如果有 f 的 面,每一个面是不是都是 n 边形,所以是不是乘以 n, 这是我所有的边数了,但是每一条边大家想想看,是不是都被重复应用了一次, 能不能想明白这个问题?是不是啊?所以呢,需要除以二啊,所以需要除以二。好,那么第二个从顶点角度出发呢,如果每个点发出的棱有 r 个, 那你想我一共有 v 个顶点的哇,我一个点都能带着 r 条棱,那所以 v 乘以 r 是 不是也是我的棱数?咱们来看啊,比如说这个点发出的一个点发出的是不是三条棱,看到了是不是?但你会发现下面这个点,再看他发出的棱是不是也被重复计算了一次,所以这里的棱是不是也全部都加倍了,对不对?所以当然也是需要除以二 这两个公式,反而是做这种题目的关键核心的。这个第一个公式倒不是核心啊,后面两个主要是做题目的一个切入点了,那么它应用也很广泛,大家也了解这个足球,这个足球是不是黑白相间,是用什么边形和几边形啊? 是不是?五边形和六边形,这个了解过吧?是不是?哎,五边形和六边形组合就完全可以来解决这种题目了,知道吧?所以这种题的关键其实是在于这两个公式上的, 在这两个公式我们再了解一下啊。好,这两个公式都是为了算这个棱数的,这个棱数的第一个奇数点呢?是通过这个面数来,对不对?如果 f 个面,每个面是不是都是 n n b a 型,是不是?所以 f 乘以 n 是 不是多的棱数,但重复了一次,所以需要除以二,对不对?好,那第二个我们从哪出发呢?哎,我们从顶点出发, 如果有,哎, v 个顶点,对吧?每个顶点是不是都会发出很多的棱?是不是?所以 v 乘以 r 除以二,也可以来算这个棱数,所以它俩都是为了来算棱数的, 这个能不能理解,对不对?好,所以一定要了解清楚啊。好,那么第三个来看一下,已知有一个多面体,有三十条棱,每个顶点连接了三条棱,请问他的面数是多少?那么这个该怎么切入? 那首先来一个多面体,有三十条棱,这个第三问,这个棱还记得英文单词吗?棱是不是 e 啊,对不对?说明 e 等于三十来,这个题每个顶点发出了三条棱,说明 r 是 不是等于三,看来想用的公式是这个了, 对不对?好,因为 e 呢,等于二分之 v, 而所以来代入一下啊。这个 e 呢,等于三十,等于二分之 v 乘以三,所以我们可以先把 v 解出来,是不得二十 v 都有了,同学们,你想求的什么?想求的是 f 呀,想求的是 f, 对 不对?好,所以因为 v 加 f 减 e 等于二,所以来代入了啊。这个 v 等于二十,加上,哎,这个 f 未知, e 呢,等于三十,所以直接就出来了, 他说点十二,这 f 面数就是十二面,那就是正十二面体吗?是不是正十二面体啊?所以这一问就求出来了,所以你看就是两组公式的一个重复性,你看你要选择哪个公式,懂了,要看选择哪个公式的啊。然后呢?第四问就比较伟大了, 让你自己来论证一下,全世界所有的正几何体,正多面体到底有几个?一共多少个?有可能说,难道不会有无数个吗?那我不是的,其实它是有限格的,我们可以坐下去问, 哎,这个如果你活在欧拉之前,哦,你比如说你穿越了,你要验证出这个你真的是爆炸性的,这个你绝对欧拉,大家都知道的吧,欧拉很伟大的,是不是你要在他之前发现的这个公式,那还得了,是不是?我们现在就来论证一下啊,到底这样的正多边题有多少个? 来看一下。那么前面的公式的推论,我们就发现了一个问题,发现什么?这两个式子是不是都是跟 e 相关的?是不是?哎,也就是说 f 跟 e 有 关, v 跟 e 也是有关的,所以这个公式里面我就可以替换了啊,咱们来看一下啊。好,根据第一个式子,咱们把 f 转化出来,是不是等于二倍的 e 除以 n, 是 不是第二个式子这个公式呢?哎,咱们把 v 转化出来,因为我都要找跟 e 的 关系嘛,一个式子我不希望未知数太多,是不是?所以我需要转化了啊,所以这个 e 呢?哎, v 呢,我们换成两倍的 e, 比上 r 是 不可以到这步?是不是好,到这之后再来看了啊?那么我原式因为 v 加 f 减 e 呢,是等于二的,所以来往里边带啊,这个 v 呢,就是二分之二, e 呢,就是 n 分 之二减去 e 就 等于二。 好,这个式子有没有观察到这个 e 是 不是都有 e? 是 不是?我们把二 e 除掉吧,好吧,哎,把每一项的两倍的 e 除掉,所以是二分之一,加上 n 分 之一,减去二分之一,就等于 e 分 之一了 啊,是不是这样的,是不是?好,那坐在这很多同学就又卡住了,当然肯定当时的欧拉也可也卡住了呀,我怎么知道其他的一共多少个呢?哎,所以他开始想了。我对于一个正多面体来说,这道题有限制的条件,一个点发出的最少是有三条, 这个 r 是 不是有范围的,是不是最少从三开始?是不是?那到底几面题呢?每个面是几边形是不也很好?从肯定是三角形开始,是不是没有两边形这说法,是不是?哎,三角形,四边形,五边形,六边形,这两个是不是都是好推论的 啊?唯独这个 e 的 话,其实他也考,你怎么知道一个正多面体到底有多少条?是不是所以我们把好推论的东西呢放在左侧,把不好推论的东西呢放在右边去 啊。首先到这之后呢,来开始继续分析了啊。哎,我们这道题的 r 是 不是有个限制条件? 这个 n 的 几面体是不是几边形?是不是有限制条件?是不是?来开始分类好了?最小最小嘛,起码这个 n 要等于三呀,我不能正两边形吧,是不是最起码三边形?这个 r 也有要求, r 最小来看大,前提这个 r 有 个条件, r 大 于等于三, r 最小值是不是等于三?是不是好?所以来当 n 等于三, r 是 不是也等于三的时候, 是不是要来?是不是?好,这个时候来我们带进去啊。这个时候你验证一下,三分之一加三分之一是不是等于一分之一?加上二分之一,这个 e 确实是可以被求出来的, 这边三分之二,然后减去二分之一,是不是六分之一,那就是六了,可以求出来,可以求出来,当然是成立的呀,是不是好?那么第二种情况,我的 n 还是等于三,但是我的 r 开始变大,变成四, 哦,变成四是不是好,那这个时候呢?就变成了四分之一加三分之一等于一分之一加二分之一来我们,所以这个 e 肯定也可以求,你看这个左边是不是等于十二分之七?这边十二分之六,所以检查出十二分之一,所以 e 呢?就等于十二 一,是不是得十二,对不对?好,那么第三种,当 n 等于三的时候, r 开始变成五了,是不是?当 r 等于五的话,那么这个式子就变成了什么呢?五分之一加上三分之一,等于一分之一加上二分之一, 好,那么左边是不是等于十五分之八,十五分之八呢?就是等于三十分之十六,是不是三十分之十五,三十分之一随意等于三十,哎,也可以也可以看到了,是不是?好再来推论啊。当 n 等于三, r 等于六的时候,所以就变成六分之一加三分之一等于一分之一加二分之一,不好意思,这个情况就要被舍弃了, 为什么?六分之一加三分之一,是不是已经等于二分之一了?是不是?所以你写的时候从这改成大于等于之后,都是要被舍掉的, 都要被舍掉了,接下来又来,是不是肯定更不符合题了?你想想看,是这样的,是不是接下来更不符合题了啊?所以 r 一 旦超过六,全部都舍去了,所以在这种情况是不就已经存在三个了,是不是?那我们继续来看啊,当 该换了啊, n 变成四了, n 变成四了啊,然后呢? r 等于三,哎,对不对?所以三分之一加四分之一等于一分之一加上二分之一,哎,还是刚刚那个,是不是?哎,这个符合题是不是好?当来, n 等于四, r 等于四,肯定舍去了, 我这个就不戴着眼镜了吧。 n 等于四, r 等于四,四分之一加四分之一,是不是已经等于二分之一了?是不是所以他不符合题,所以大于等于四都舍去了, 在这种情况下,只有一个啊,只有一个,好,再来推论,当 n 等于五的时候,反而还是从三开始,对不对啊?所以五分之一加三分之一等于一分之一,加上二分之一,所以一等于三十,哎,有一个成立了,是不是 好?一,当 n 来再等于五, r 等于一等于一等于一等于一等于三十。一啊,不好意思,不符合题了, 舍掉了吧。因为这边是二十分之九的,没有超过二分之一吗?是不是所以被舍去了啊?被舍去了,被舍去的话,说明大一点。四,接下来是都复合题了,是不是?好,接下来当 n 等于六, r 等于三的时候 啊, n 等于六,那肯定舍去了,因为六分之一加三分之一,是不是?所以接下来都不需要再讨论了,接下来全都舍去了,已经再也不存在了,接下来肯定都不行了,是不是?所以综上所述,它就论证出来了,自然界中所有的正多面体不是无穷多个的, 它是有限格的,只有几个呢?只有五个,当然能算着,是不是只有五个,是不是?哎,你也颠覆你的认知,你也觉得,哎,就这种多媒体不应该是无穷无穷多个吗?那不是的,知道吧。哎,它只有有限格数,所以只有五个,只有五个,听懂了啊,它是只有五个的啊, 哎,这道题你说啊,比如说我今年中考的时候结合到这个题干里面去,是不是?哎,因为这个东西最近很火的呀。哎,这个欧拉多媒体公式我可以完全结合一下,对不对?让你自己去推论啊, 对不对啊?他情况比较多啊,情况比较多,所以他是通过 r 和 n 去做推论的啊? r 和 n 去做推论的,呃,那么这道题,呃就整理完吗? 写好了吧,能理解吧啊,其实这道题呢,其实大家主要是理解这两个公式啊,就是这边这两个公式你只要背会 v 加 f 减一等于二,知道吧?哎,然后呢,这两个公式要去深入理解一下,知道吧?哎。然后我们来看一道七年级的题,你不要觉得啊,七年级这个题不考吗?我们先把这个讲完再啊,你看这道题 是不是几乎一模一样的。七年级最近也在考啊。这个东西呢,我,我肯定从后面一看,这个东西都不要管了, v 加 f 减一肯定是等于二的, 是不是这样的是不是?好,然后再来看,哎,有一个正多面体的棱数比零点数大,十有十二个面,问他棱数,你看是不是求棱数的?我们刚是不是做了两个推论,是不是?好,那这道题毕竟给我面熟了。来,回想一下,正十二面体的图,正好在这正十二面体有十二个面,你观察一下这个十二面体的每个面都是几边形的? 五边形,所以是不是乘以五。本来来说的话是六十条棱的,但要除以几,哎,对二,因为每一条棱是都会重复应用了一次,所以最快速的方法知道题是用这个思路是更简单。但有的人就说啊,老师,我不想用这个,我要用每个顶点发出,假如说有 x 个顶点 好, x 的 顶点每个顶点发出,你看看每个顶点发出是三条等,对不对?好,所以是三。 x 是 不是也要除以二?是,是等数呀,听过吧,是不是每个点发出三条等,所以二分之三 x 也是什么数呢?也是等数,对不对?好,所以这里的顶点数 x, 那 等数是二分之三 x, 所以 它减它的也是 x, 是 不是也可以减起来? 听我一说啊,好,继续。主要是这个第三个来看一下啊,某一个这个玻璃饰品啊,它是由三角形和八边形构成的。好,然后每个顶点处呢,都有三条棱,你看这个就知道要,所以要从顶点切入了,是不是?好,然后呢?一共有三十六条棱来,棱是用 e 表示的, e 等于三十六,刚刚我们说了, e 是 不是等于二分之 v? r 量 r 指的是每个顶点发出几条棱,是不是来代入一下,所以三十六就等于二分之 v 乘以三,因为每个顶点发出了三条棱,是不是好,所以 v 就 可以被解出来了, v 有 了, e 有 了,因为 v 加 f 减 e 是 等于二的,所以带进去 f 能不能说出来?可以了吗?是不是?好,所以 v 是 二十四啊, f 未知, e 呢三十六, 所以 f 呢就等于十四了,所以这个多面体的面数是一共就十四个,这个面呢是由三角形和八边形构成的,那你看这我八边形乘成 x, 我 的三角形不就是二 x 加二个吗?他们一共有十四个,所以 x 不 就解出来了吗?那你要的二 x 加二不就也有了吗? 听懂了吗?这道题放在考试中啊,班上就是你,比如就是你现在来考这个,最后一个真的去做的话,一个班不会超过三个多月把它做对了啊,这个题难度系数还是比较高的,懂了吧?哎,所以你看我给大家讲的时候,其实我站在哪个维度去讲的?我其实用的这个就是这两个公式,大家要首先去理解再去做题。 听懂了啊?要不然你只用这一个公式的话处理其实太显险了,我们要从顶点和面去反推这个公式,再去处理题目。听懂了啊,这个题目过了吧?好吧。
52扬州梁欢数学
猜你喜欢
- 1967小鲨鱼玩游戏
最新视频
- 10.0万粉粉莓烦恼







