10保7旋转矩阵公式详解
今天呢,我们介绍一个就是大家经常问的一个问题,我们称之为二维空间上的坐标,项链福数,极坐标,以及他们的一些运算。我这个比较简单啊,就是要回答一个同学的问题, 我们现在给出一个平面,只有坐标系上面有一点叫 a, 他的横坐标是 x, 纵坐标是 y, 但是啊, 对于我们来说,你给出他这个坐标,他是不能运算的,两个坐标相加还相减,不能处理,所以为了能够对他进行处理,我们进行了一个新的定义,那就叫项链, 给出了项链,一般项链都是立着写的,是不是?哎,立着写这个项链有好处啊,项链可以跟有什么好处? 项链就是可以,这个可以,这个有加法和速成啊,现行运算吧, 所以就比原来的坐标好多了,是不是?哎,比原来坐标好多了,但是啊,他也仅仅有加法和数乘,仅仅有这个现行运算,所以就叫现行代数吗? 是吧,那么只有这个加法和数乘还不够,其实在我们微积分的数中啊,其实还给出了另外一种东西,就是极坐标 级坐标是什么呢?我,我给学生就举例子时候说过,你一说,哎,你的同学,今天星期天你同学来了,说 说你在哪呢?他说我在东京啊,一百一十五度,北纬四十二点三度,在这等你呢,你上哪找他去?他说,我在你正前方二十五米那个 位置,或者是正前方偏左十五度三十米那个位置,你不马上就知道了吗?所以极坐标啊,比较容易就以你为中心,你的前方是正方向,往左往右 找角度吗?所以我们这个呢,就是 x 轴正半轴,正半轴是正方向,然后逆时针 为角度,距离是 r, 这样 r 和 c 的就是极坐标,不仅有了极坐标,其实这个只有坐标系和极坐标其实是可以互相转化的,但是也不够,还是不够。 不够什么?他只有加法和数乘等等一些运算还不够。所以我们在中学的时候啊,其实是添加了一个种运算,叫复数运算。这个复数运算就是把横坐标呃,叫 x, 纵坐标叫做 y, 那么 x 加 y i 就是福数。其实大家仔细想,这个其实还是个项链吗?是不是就是 x 乘以一零加上 y 乘以零一吗?只不过我们现在把一零叫做一,把零一叫做 i 吗? 这就是项链运算的一个好处。但是写成复数,再加上这个级坐标,我们就可以给出一叫做啊复数的三角表示,是不是?哎,复数的三角表示, 那就是 r cosine 加上埃 cying, r 就是膜,这个 c 的就是辅角,其实就是极坐标象镜 和这个犄角,但这样还不行,还有人继续往下坐。那么数学的伟大就在这,把这个靠三年级再加上 i 乘以三年级的,用指数的 形式表表示出来,就变成了 r 乘以一的 ic 的。这个在电子学院啊,计算机学院软件,呃,那个这个就是功课了吧,电器呀,机械呀,用的非常多, 怎么用?它主要用于乘法、除法、 n 次方、 n 次密等等运算。你看这一和这二,我们要把它写成指数的形式。那两个相乘就是 膜和膜相成,辅角和辅角相加吗?相处呢,就是膜和膜相除,辅角和辅角相减吗?所以这个东西很容易了是不是? 哎,很容易给出来了,包括纸刺、这个,这个蜜呀等等都可以这么做了,所以普通的服数加减好办。但是啊,乘除纸 蜜啊,方蜜等等就得用到指数形式。不仅如此,我们还可以给出另外一个运算,就是很多同学问他说说这个平面上有一个项链叫 o a, 还有一个项链叫 o b, 这个 a 到 b 啊, a, a 逆时针旋转到 b, a 逆时针旋转头, b, 这个膜都没给我变嘛。所以 z 一和 z 二就是 a, 就是 z 一嘛, o a b 就是 ob, 就是 z 二, 你会发现,其实这个 o b 呀,或者 z 二就等于 z 乘以一,呃, z 一乘以 z, 那这是什么?这就是普通的一个辅数,他普通到他的膜是一,辅角是 c 的,你看见没有?根据这个几何性质,简单就是给出来了。那不仅仅可以简单给出来, 我们把它展开,会发现这个 x 二和 y 二被 x 一 y 一表达出来,仔细一看,这不是一元一二阶线性方程组吗?那如果是二阶线性方程组,那不就写成矩阵的形式吗? 是不是你写成句阵式形式,你发现没有, x 二 y 二等于 a 乘以 x 一 y 一,这个 a 就是我们刚才说的旋转的模型,是不是就这个旋转的模型?那么你仔细看,这个 a 并不仅如此,他还竟然是一个 正焦震,哎,正焦震。所以呀,我们说如果转的不是这个 c 的脚是 n c 呢?那就把它改一下吧。而这个 n c 呢,恰好是 a 的 n 次方,所以,哎,我们要转 nc, 他转转转, n 个 c, 事实上就是 a 的 n 次方,乘以 x 一 x 二, x 一 y 一,我说丢了个等号,是不是?哎?丢了个等号。好,我们今天就讲到这。
粉丝1519获赞9483
相关视频
 05:25
05:25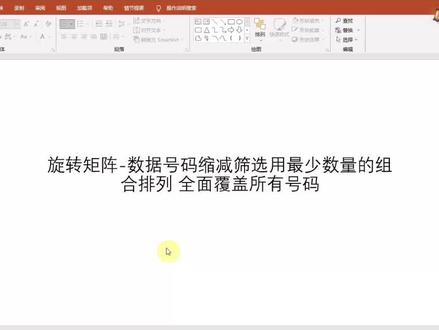 02:38查看AI文稿AI文稿
02:38查看AI文稿AI文稿各位老铁大家好,这一期我继续为大家讲解这个旋转矩阵。旋转矩阵的数学原理非常的复杂,我这里就不多赘述了,这里主要讲一下旋转矩阵给我们实际带来的一些好处,主要的一个好处就是可以 呃大量的缩减这个组合的呃数量,让我们既满足嗯号码全面覆盖的同时,又让所产生的组合尽量的少。那我们就直接拿一个例子,通过例子来说明一下, 比如我们现在有八个代选的号码,一二三四五六七八,希望就是说,嗯,我们随便说一个任意的三位号码都必须包含在某一个五维的号码当中,也就是说首先 我们是八选五组成,嗯,五位一组,五位一组的这个号码,然后希望这些所有五位的号码覆盖了所有的三位的号码,那么需要多少个这样的五位的号码才能覆盖所有的三位数呢? 我们可以用工具计算一下,这是一个八选五的一个计算工具,我们点击计算发现有五十六组,总共计算下来就是说有五位数这样的组合,一共五十六组, 就包含了所有的三位数的号码,这个数据计算下来还是比较大的。那我们再看一下,如果通过旋转矩阵的方式计算下来,要覆盖所有的三位数,总共有多少号码呢? 通过我们的旋转矩阵公式,我们选中了八个号码,然后点击计算可以看到一共生成了八组,这八组号码就包含了任意的三位数,从八个数字当中选的任意三位数 我们可以看到,嗯,就是说通过旋转矩阵的组合方式计算,让我们的号码组合从五十六组缩减到了八组,多达七倍多的缩减,这是一个巨大的节省, 所以我们要充分的学习和利用好旋转矩阵的公式的话就可以。嗯,在 达到全面覆盖所有结果的同时,又减少勇于的组合,做到最优的一个计算,嗯,这一期就到这里,谢谢大家。
 00:37查看AI文稿AI文稿
00:37查看AI文稿AI文稿什么是旋转矩阵?借用电脑手段来选择的一种叫做旋转矩阵,用这个方法呢,就是说把你喜欢的这种某一两个号码作为胆的号码, 就说你的幸运数字也好,然后呢,通过电脑把你这个号码输进去,用旋转矩阵这个软件测算出来, 给你一次排列出来的号码,这是一种通过电脑进行号码的一种组合的数学优化方式,但是呢,这种不是包括复式,指的是单次号码选择,买单次的时候呢,作为一种参考方法吧,关注我,沾喜气!
226河南省体育彩票管理中心 07:38查看AI文稿AI文稿
07:38查看AI文稿AI文稿大家好,欢迎来到工程形象,对于旋转矩阵,大家有没有这样的感受?学习的时候感觉不难,但实际使用的时候晕头转向。什么情况下要左成,什么情况下要右成? 什么情况下要转制?本期视频将带大家形象直观的理解旋转矩阵。 第一天,在一片虚无的三维空间,神说要有一个点,于是就有了一个点屁,人类开始思考,上帝开始发笑,如何在三维空间表示这个点呢? 我们建立一个直角坐标系 s, 三个轴分别为, x, s, y, s, z, s, x, s, y, s, z, s。 方向上的单位向量在坐标系 s 中分别表示为, e, s 点 x s, e, s 点 y, s, e, s 点 c, s, 构成一组标准单位向量。以坐标系的原点为起点,指向点 p 所构成的向量 p s 表示点 p 相对于坐标系 s 的位置, 分别使用三个标准单位像量与 ps 进行点击运算,可以得到 ps 在三个坐标轴上的投影, xps, yps, zps。 将三个点击运算写成一个矩阵乘法运算可以看到三个标准单位向量构成一个单位矩阵。在坐标系 s 中, x, p, s, y, p, s, z, p s。 构成一个坐标,表示 p s。 第二天,神说要在坐标系 s 中旋转,点 p 如何表示这次旋转呢?我们先复制一个坐标系 s, 即为坐标系 b, 称 s 为参考坐标系 b 为本体坐标系点 p 相对于 b 固定不动,然后相对于 s, b 随着点 p 一起同步旋转,因此 p 相对于 s 的旋转等价于 b 相对于 s 的旋转。在坐标系 b 中, p b 表示点 p 的位置。使用 p b 在 x b, y, b, z b 上的投影 x p b y p b z p b 构成一个坐标来表示 p b。 在坐标系 s 中, x b y b z b 方向上的单位向量分别表示为 e s 点 x b e s 点 y b e s 点 z b。 该组单位向量相互正交,并且在空间位置上与 s 中的标准单位向量组具备相同的属性。分别使用三个单位向量与 p s 进行点击运算, 可以得到三个投影, x p b y p b z p b。 将三个点击运算写成一个矩阵乘法运算,可以看到三个单位项量构成一个行列式等于一的特殊正交矩阵。 利用正交矩阵的逆等于其转制的性质,得出 p s 等于 r s, b 乘以 p b。 其中 r s b 是一个三乘以三的矩阵,称为坐标系。 b 相对于 s 的旋转矩阵,表示 b 相对于 s 的姿态。 x b y b z b 方向上的单位向量在坐标系 s 中的表示构成矩阵的三列。因此, r s b 是一个行列式等于一的特殊正交矩阵。利用矩阵的逆运算法则和正交矩阵的性质,得出 r b s 等于 r s b 的逆等于 r s b 的转制,即旋转矩阵的转制,表示 逆向的旋转和姿态。第三天神说要在坐标系臂中旋转点屁,为了让点屁相对于臂固定不动,我们先复制一个 b, 即为 b 一撇。 这样我们就可以将 p 相对于 b 的旋转转化为 b 随着 p 一起相对于 b 一撇的同步旋转。 此时 b 一撇相对于 s 的姿态,等于 b 相对于 s 的姿态,然后 b 一撇保持不动。相对于 b 一撇, b 和 p 一起同步旋转, 该旋转产生的旋转矩阵为 rb 一撇, b 由于 s 和 b 一撇都保持不动,所以 b 一撇相对于 s 的姿态保持不变。旋转后点 p 相对于 s 的位置等于 b 一撇相对于 s 的姿态乘以 p 相对于 b 一撇的位置。 其中 p 相对于 b 一撇的位置等于 b 相对于 b 一撇的姿态乘以 p 相对于 b 的位置。综合以上两点,得出 p 相对于 s 的位置等于 b 一撇相对于 s 的姿态乘以 b 相对于 b 一撇的姿态乘以 p 相对于 b 的位置。 使用矩阵乘法的结合率得出 b 相对于 s 的姿态等于 b 一撇相对于 s 的姿态乘以 b 相对于 b 一撇的姿态。这里解释了在本体坐标系中旋转本体坐标系为什么要又乘。 第四天神说要在坐标系 b 中旋转坐标系 s, 我们先复制一个坐标系 b, 即为 b 一撇,此时 b 一撇相对于 s 的姿态等于 b 相对于 s 的姿态。 然后相对于坐标系 bb 一撇随着 s 一起同步旋转,因此 s 相对于 b 的旋转等价于 b 一撇相对于 b 的旋转,该旋转产生的旋转矩阵为 rbb 一撇,并且 b 一撇相对于 s 的姿态保持不变。 旋转后 b 相对于 s 的姿态等于 b 一撇相对于 s 的姿态乘以 b 相对于 b 一撇的姿态。其中 b 相对于 b 一撇的姿态等于 rbb 一撇的转制。这里解释了在本体坐标系中旋转参考坐标系为什么要又成转制。 第五天神说再次在坐标系 s 中旋转点 p, 我们先复制一个坐标系 s, 即为 s 一撇,此时 b 相对于 s 一撇的姿态等于 b 相对于 s 的姿态,然 后相对于坐标系 ss 一撇随着 b 和 p 一起同步旋转,因此 b 和 p 相对于 s 的旋转等价于 s 一撇相对于 s 的旋转, 该旋转产生的旋转矩阵为 r s s 一撇,并且 b 和 p 相对于 s 一撇的姿态和位置保持不变。 旋转后, b 相对于 s 的姿态等于 s 一撇相对于 s 的姿态乘以 b 相对于 s 一撇的姿态。这里解释了在参考坐标系中旋转本体坐标系为什么要做成。 第六天神说,要在坐标系 s 中旋转坐标系 s, 我们先复制一个坐标系 s, 即为 s 一撇,此时 b 相对于 s 一撇的姿态等于 b 相对于 s 的姿态,并且 s 相对于 自身的旋转等价于 s 相对于 s 一撇的旋转,然后 s 一撇保持不动, s 相对于 s 一撇进行旋转,该旋转产生的旋转矩阵为 rs 一撇 s 由于 s 一撇和 b 都保持不动,所以 b 相对于 s 一撇的姿态保持不变。旋转后, b 相对于 s 的姿态等于 s 一撇相对于 s 的姿态乘以 b 相对于 s 一撇的姿态,其中 s 一撇相对于 s 的姿态等于 r s 一撇 s 的转制。 这里解释了在参考坐标系中旋转参考坐标系为什么要左乘转制。 第七天神说 leave me alone 好的,本期视频到这里就结束了,感谢您耐心看完,有什么问题的话,欢迎留言讨论,如果您喜欢这类视频的话,麻烦动动手指点个关注吧,我们下次再见!
148工程形象 00:46查看AI文稿AI文稿
00:46查看AI文稿AI文稿旋转矩阵是科学,不是玄学,也不是某些老铁说的转呀转呀的,开上号码就转出来了。实际上它是一种组合设计,叫做覆盖设计。而覆盖设计、填装设计、斯坦纳系和 t 设计都是离散数学中的组合优化问题, 他们是解决如何组合集合中的元素达到某种特定的要求啊,这其中最关键的就是算法, 我们普通人学习散法确实是比较困难,但是好在现在有非常好的那种封装好的工具,我们只要学会使用这些工具就可以了。 在我们玩大乐透双色球或者是一些组合排列类的游戏啊,都可以利用旋转矩阵中的组合设计进行号码缩水,降低成本啊,这很关键,很有用,也很有意思。
202店主阿敬 01:14
01:14 04:15
04:15 04:52
04:52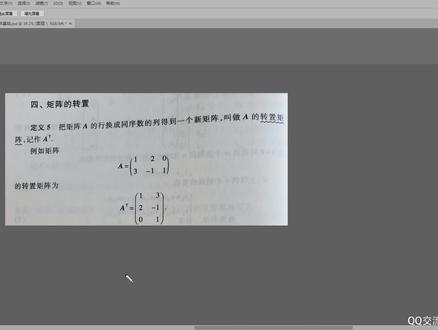 03:30查看AI文稿AI文稿
03:30查看AI文稿AI文稿大家好,我是小宅。第二十讲呢,我们来讲一下矩阵的转制公式。首先呢,我们看一下书中给的转制矩阵的定义,一个矩阵 a, 他的行换成同序数的列,得到的新的举证就叫做 a 的转制举证,记做什么呢?记做一个 a 加上 t 啊,说的简单点吧,就是一个举证的行变成列, 这个行呢变成这个列构成的新的这个举针继承 a t, 那么这个矩阵呢,就叫做圆矩阵的转至矩阵,那么在转至矩阵当中呢,有一个特殊的矩阵,如果一个矩阵转至之后, 和原来的矩阵一模一样,完全相等,那么这样的一个矩阵呢,就叫做对称举阵。那么对称举阵呢,他的第一个要求呢,首先在 这个矩阵必须是一个方阵,在这种情况下,你转着之后还等于你自己,那么你就叫做对称矩阵,简称呢就叫对称阵。那么我呢 在网上呢,找一个简单的图片我们看一下,可能不太清楚,但是不影响我们来看啊,比如说当前的这个举针,你如果把这个举针行变成了列, 对吧?那你会发现呢?哎,这个列和他原来的这个行的数字呢,是一模一样的,这个呢实际上就叫做对称阵, 大家呢可以看这个图,大致呢自己转一下,就可以理解到他为什么叫对称矩阵了,而且大家仔细观察的话,对称矩阵呢,他以对角线为中心, 其他的这些元素大家仔细看都是一模一样的,也就是它是完全对称的, 这个呢也是判断对称矩阵的一个重要依据。那么接下来呢,我们来看一下矩阵转至当中的常见公式,第一个呢,就是一个矩阵转至之后,再转至依然等于他自身,这个也很好理解,对吧?比如说呢,当前有一个矩阵,他其中有一行, 这个矩阵,你转至之后呢,肯定呢,我们当前的这一行就变成了一列了吧,那么变成一列的这个矩阵再转至,那么当前的这一列呢,他怎么样又会变成一行? 说白了吧,就是同样的这一个元素,你先把它由横变成竖,然后呢,又从竖再变成横, 他没变化呀,所以说呢,这就是一个矩阵经过两次转至,还等于他自身,这个也很好理解。然后呢,看第二个一个数乘以矩阵 进行转至,等于这个数乘以转至后的矩阵。那么关于这个公式呢,也很好理解,我们之前就说过一个数,对吧?一个数如果乘以一个矩阵的话,等于这个数呢,乘于矩阵中的每一个元素。 那么我们一定要知道,这个矩阵在转至之后呢,只不过呢,是行变列或者裂变。行 矩阵当中的每一个元素是不变的,既然每一个元素不变,那么一个数乘以矩阵就等于这个数乘于矩阵的转至。为什么?因为矩阵当中的元素不变,转至之后的元素也没有变。 这个呢,是理解这个公式呢,非常简单的方式。那么最后呢,两个矩阵相乘,两个矩阵相加的这个转制呢?我们后面通过一个例题呢,再来加成理解。大家呢,现在呢,先记住这个形式。 这讲呢,我们主要介绍的是举证的转职公司,下讲呢,我们通过例题来强化对这个公式的认知。好,这讲呢?我们先到这里。
8cf 05:4311人宅
05:4311人宅
猜你喜欢
- 1735茶水蛋崽







