这个视频咱来学习一下速度与速率的区别。前面咱已经学过了速度,速度 v 是由 v、 e、 x 与时间 t 的比值定义得来的,你还知道顺时速度、平均速度等,这时候你就该问了,初中学过的路程 l 与所用时间 t 的比值该叫什么呢? 咱们现在就给他一个名字,叫做平均速率,也用字母为表示。路程是个标量,所以平均速率也是个标量。那么平均速率与平均速度有什么关系呢?他会不会是平均速度的大小呢? 看这样一个例子,一个物体沿着一个圆周运动,圆的半径为五米,物体从 a 点出发,经过五秒,第一次到达 b 点,先求平均速度的大小和方向,求平均速度需要的是位移,位移就是从 a 指向 b 的有向 线段,半径五米,所以这段长就是十米,再比上时间五秒,就是平均速度大小等于两米每秒,方向 u a 指向 b, 这样就求出了这一段的平均速度。 再来求平均速率,那就需要路程,路程就是这一段的长度,它的大小是派乘以二,再比上时间五秒,就是平均速率得三点一四米每秒, 平均速度大小是两米每秒,平均速率是三点一四米每秒。这俩显然不一样,只有单向直线运动这一段,位移大小等于路程,此时平均速度大小才等于平均速率。 接下来,如果置点又经过十秒,从 b 绕圆周第一次回到 a 点,那么内衣变成了 从 b 指向 a 的有向线段,但大小跟刚才一样,还是十米,时间变成了十秒,所以平均速度大小就是一米每秒,方向由 b 指向 a, 这十秒内路程变成了这样,大小跟刚才一样,时间变成了十秒,平均速率就变成了一点五七你每秒 这样后一半的平均速度大小和平均速率就都算出来了。那么再考虑整个前后十五秒的过程这点呢?总为一为零,故平均速度也为零。但平均速率等于总路程二派二与总时间十五秒的比值,即二点零九米每秒。 看看刚才两段的平均速率,分别是三点一四和一点五七。二点零九,不是三点一四和一点五七的平均值。也就是说,整个过程的平均 速率并不是前后两段过程平均速率的平均值。说完了平均速度与平均速率的区别,再来看看顺时速度与顺时速率。由于顺时速度可以看作极短时间或位以内的平均速度,因此顺时速率也就可以看作极短时间或路程内的平均速率。 这里我们发现,在极短的世界或位移里,位移的大小就是路程,所以顺时速度的大小就是顺时速率,常常直接简称为速率。 因此,测量或估算物体的速率,往往需要测量物体运动哪一小段时间得是 t, 并测量这一小段时间呢?为一大小得是 x, 再进行计算,这也是现代许多测速仪器的工作原理。 好了,总结一下这个视频,我给你讲了速度与速率。平均速率是路程与该路程对应时间的比值。当时间极短时,平均速率就是顺时速率, 简称速率。速率表示顺时速度的大小,但平均速率却不是平均速度的大小。如果把四个概念放到一起,总结下来就是,平均速度和平均速率对应于某段过程对同一段过程,平均速率大于等于平均速度的大小。 顺时速度和速率对用于某个时刻或某个位置,二者总是大小相等。左侧两个是标量,右侧两个是使量。好了,都清楚了吗?快去刷题吧!
粉丝235获赞1122
相关视频
 02:42查看AI文稿AI文稿
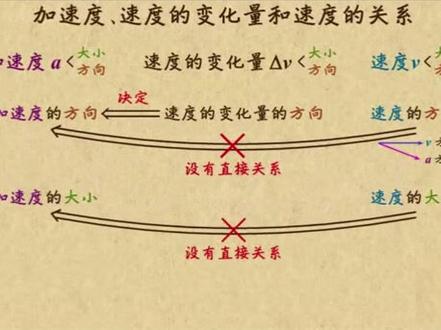
02:42查看AI文稿AI文稿之前的视频中经常提到三个物理量加速度、速度的变化量和速度。这一次咱来比较一下他们之间的关系。 他们三者都是使量既有大小又有方向。加速度的方向是由速度的变化量的方向决定的,但是跟速度的方向没有直接的关系, 他们之间可能相同,也可能相反,还有可能成一个普通的假角。除了方向之外,加速度的大小和速度的大小也没有直接的关系。一个物体可能速度很大,但加速度很小,甚至为零。 比如高速前进的飞机,他在平稳飞行的过程中,速度非常大,但是加速度是接近于零的。同样,物体也可能速度很小,但是加速度很大。比如炮弹发出的瞬间,他的速度还很小,但是此时他的加速度却 非常的大,经过很短的时间,速度就会变得非常大了。最后咱们看看加速度的大小和速度变化量的大小,影响他们之间关系的因素就是时间。 咱来看这个例子,在跑道上,一架飞机和一辆摩托车比赛,看谁更快。最开始摩托车明显比飞机快,但是后来飞机越来越快,终于大大超过了摩托车的速度。 在这个过程中,飞机的加速度比摩托车小,但摩托车只加速了一小会就变匀速了,而飞机持续加速的时间非常长,它的速度的变化量最终就会非常大。 好了,这三者的关系咱已经说清了,现在你来思考一个问题,有没有一种运动物体的加速度越来越小,但是它的速度却越来越大呢?可能你已经想到了,比如一辆正在公路上加速的小轿车,司机开足了油门, 开始的时候,这辆轿车的加速度非常大,你作为乘客坐在上面感到了俗称的推背感。但是汽车的加速度不能一直这么大,他会越来越小, 可是加速度与速度方向却始终是相同的,那这辆汽车的速度就会一直在增大。到了一定的速度后,由于能量输出的限制,这个汽车没办法再加速了,他就会维持匀速直线运动,此时加速度也就变成零了。 说完了这个问题,你再思考一下另一个问题,有没有加速度越来越大,但速度却越来越小的例子呢?对了,还是以驾驶汽车为例,如果司机发现前方出现了危险,会踩刹车踏板,也许有些时候司机踩刹车的力度会逐渐加大, 汽车处于减速状态,而且减速过程中加速度的数值越来越大,但是由于加速度跟速度方向是相反的,所以这辆 的速度却是越来越小了。好了,要讲的就这么多,这个视频我就给你讲了,加速度、速度的变化量、速度三者的关系,你都弄清楚了吗?快去做练习题吧!
982物理马老师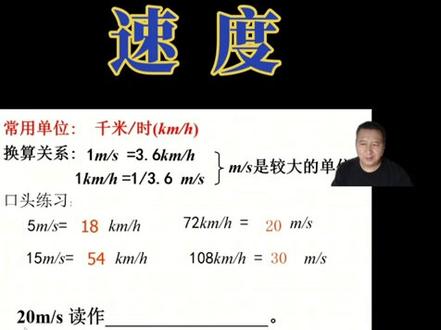 03:06查看AI文稿AI文稿
03:06查看AI文稿AI文稿初中物理速度,在物理学中,我们用速度来表示物体运动的快慢,这也是速度的物理意义。我们来看速度的定义。我们用 单位时间内通过的路程表示速度,那么速度就可以表示为速度等于路程除以时间。 如果我们用 v 表示速度, s 表示路程, t 表示时间,那么速度的公式可以表示为 v 等于 s、 b、 t。 我们上节课学习路程,他的单位是米, 时间的单位是秒,那么速度的单位国际单位是米每秒,那么它的符号可以写为米杠 s 或米点 s 负一。 除了米每秒以外,我们速度还有一个常用的单位千米每小时。 那么千米每小时和米每秒之间的换算关系非常重要,我们来看一下。 那么一米每秒等于三点六千米每小时。也就是说你将米每秒画成千米每小时的时候,让他乘以三点六就可以了。 反之,千米每小时画成米每秒的时候除以三点六。那么从画展关系上我们可以看出来,米每秒是一个较大的单位。我们来做一个口头练习。 五米每秒等于多少千米每小时?按照我们上面的换算关系,米每秒画成七米每小时乘以三点六,五乘以三点六,应该是十八千米每小时。 七十二千米每小时画成米每秒,我们可以除以三点六,因此是二十米每秒。十五米每秒画成千米每小时乘以三点六, 应该是五十四千米每小时。一百零八千每小时化成每秒除以三点六,应该等于三十米每秒。 二十米每秒,我们读做二十米每秒。 二十米每秒的物理意义是什么呢?他表示该物体每秒运动的距离为二十米。我是物理张老师,点个关注,少走弯路。
67张老师·安徽高考 04:13查看AI文稿AI文稿
04:13查看AI文稿AI文稿什么是速度?很多同学会直观的给出答案,速度等于路程,除以时间。我们需要注意的是,物理不但是一门复杂的学科,也是一门精细的学科。 我们小学、初中时学到的速度和高中时所学的速度根本就是两个完全不同的概念。那么什么是速度? 速度是描述物体运动快慢的物理量,物体运动的速度越大,就表示运动的越快。比如两辆汽车同时出发,经相同时间走的远的那辆速度快过两辆车在一段相同的路上行驶,先走完用时少的速度快。 物理上我们用 v 表示速度,求解公式是 v 等于 x 比 t, 公式中 v 表示速度, x 表示位移, t 表示时间。简单来说,求解速度就是物体运动发生的位移和发生这段位移所用的时间的比值。 速度单位是米每秒或千米每时,二者的换算关系是,一米每秒等于三点六千米每时。 需要注意的是,以上公式求解的是平均速度。比如一辆汽车在一平直公路上用二十秒行驶一百米,那么汽车行驶的平均速度 v 就等于一百米以上,二十秒等于五米每秒。 这个五米每秒指的是汽车发生这段位移的平均速度。汽车在这段路上行驶时,各时间段、时间点的速度可能一直在变,所以这个速度不能指在各个 时间点时间段的速度。那么问题来了,这个时间点或者说在某个位置,物体的速度怎么表示呢? 我们把物体在某个位置或某个时间点的速度叫做顺时速度,他反映的是在某一时间点或某一位置处物体运动的快慢程度,速度质量有大小,有方向, 平均速度方向就是位移方向,而顺势速度方向就是某一时间点某一位置出的速度方向。比如遗物体从 a 点沿红色路径运动到 b 点, 那么全程的平均速度方向就是 a 指向 b 的位移方向,而在 c 点的顺时速度方向则是该点的速度方向,就是运动轨迹的切线方向。还有我们平时所说的速度,可能是顺 速度,也可能是平均速度。比如火车制动时的速度是二十米每秒,火车以二十每秒的速度通过这段铁路,前者是顺时速度,后者是平均速度,具体情况要联系上下文进行判断。 顺时速度始终为零,那么表示物体从没有运动过,说明物体静止,但是平均速度为零,物体不一定静止。比如这种情况,物体从 a 运动到 b 位移为零,平均速度为零,但物体却一直在运动。 好了,到这不知道你们有没有想过这样一个问题,既然我们以上所说的才是速度,那么小学初中学到的到底是什么?哎,没错,是速率,简单来说就是速率等于路 乘除以时间,物理通过某段路程与通过这段路程锁定时间的比值。当然这个求解同样是平均速率,而物体在某一时间点或某一位置处的速率叫做顺时速率。速率呢,是标量有大小没方向。 物理在运动时位移肯定小于等于落成,那么只有做单方向直线运动时,位移才等于路程。因此平均速度大小一定小于或等于平均速率,肯定不会大于平均速率。 物体在某一位置的顺时速率就是该位置顺时速度的大小。好,今天的内容就到这里,那么你学会了吗?
112倒霉猪 08:51查看AI文稿AI文稿
08:51查看AI文稿AI文稿欢迎来到物理大师,今天我们学习第一张运动的描述。速度, 速度,我们用位移与发生这段位移所用的时间之比,记着是位移与发生这段位移所用的时间之比 叫速度。位移是什么?位移是位置的变化, 那如果我们是位于与发生这段位于所用的时间之比,实际上是不是就是位置的变化与发生位置变化所用的时间之比呢?那是不是就是我们可以用来 研究你位置变化快慢了呢?哎,这个速度的定义和我们初中阶段定义好像就不太一样了,那初中阶段我们描述的是路程比上时间,但是在这里面我们发现是为你比上时间, 那就说我们描述的是位置变化与时间的关系啊。那我们用什么来表示时间呢?得他替,如果在得他替的时间内,锅体的位移是得海 x, 那么速度位应该等于什么?哎,对,应该是等于得他 x 比得他 t, 也就是说他应该是为你与 发生这段位于所用的时间之笔。好,那在这里呢,我们来探讨几个料, x 是什么?我们通常说的 x 是指的是位置, 那得来的 x 呢?是位移 打卡, x 比打卡器呢?是?位移比上时间 代表的是速度,这三个量代表的是完全不同的意义。我们研究哪些机械运动研究的是位置随时间的变化,我们根据位置的变化得到了位移的概念, 又是为了我们要研究未知变化的快慢与神的关系,隐弱素质概念,所以三个是相乘的,同学们一定要注意区分 x 得卡 x 与得卡 x 比得他 t 之间的关系是怎样的?不要搞混,三个基本无力量。 好,那我们继续那常用的单位位移有米。好,我换一个粗一点, 演的比时间的单位是秒,所以未雨的单位有你没秒, 或者是这样的一个符号。那同学们一定要注意,在整个高中物理学的过程当中, 在给公式的时候,我们的单位是可以进行复合运算的,那位移的单位是米,使用单位是秒,那么顿顿数单位就是你没秒单位和亮钢针的转化,同学们是一定要掌握的。 那常见单位还有哪些呢?那位于我们可以用签名去表示对时间呢?我们可以用啊,用小时,所以 他的成员单位还有千米每小时,当然如果距离比较小的时候也有米每秒,这个是我们在后续学习打点计时器的时候用的,可能会比较多一点,但是我们生活中多用的就是米每秒和千米每小时。 好,那这样的话,我们来回顾一下,那同学们走路正常的时候速度是多少 啊?有人说是一米每秒啊,也有人说是一点五米每秒,这个问题都不是特别大,因为我们正常人一步 是五厘米,你一秒钟基本上可以走两步左右啊,五十厘米一秒钟基本上可以走两步左右,所以你正常步行的速度是一米每秒也行,一点五米每秒也行。那 动车的速度呢?哦,这个是不太一样的,因为有的路段动车的速度不太一样。有三百八的啊,单位是什么啊?前面每小时啊,还有人说他做过三百九十五前面每小时的。 好,那这是我们常见的速度,同学们一定要有一个概念,初中阶段经常会考这种题目,高中我们基本不会再做这方面的要求,我们继续。那他的意义是什么? 我没了。看他的定义,他是用位移与时间之比, 那得他 x 比上得他 t, 他指的是什么?是位置电话的话 慢,记着,他指的不是未知的变化,他是未知变化的快慢,因为他是位移比上时间,是一段位移比上所用的时间, 所以他用的是描述物体位置变化快慢的物理量。 那变化快慢,初中阶段同学们有没有学过一个叫绿,与时间有关系呢?所以我们有的时候会把速度叫一个概念, 叫什么呢?叫位置电话路, 叫未知变化路,这点同学们一定要注意。也就是说你速度描述的是未知变化的快慢,是未知变化与时间的笔直, 所以我们有的时候把它称之为是位置变化率。好,我们继续。 那如果是速度越大,代表的是什么呢?是位置变化的越,这个一定要注意啊,他代表的是越快。是速度越大,代表 有的是位置变化的越快,而不是位置变化的越大。是指运动的越快。你速度越大代表的是 dota sbst 越大,它应该代表的是 运动的快和慢。是位置变化的快和慢,而不是位置变化的大小小。因为还有个时间, 这里一定要注意。也就是说当他的物体已经描述的是物体位置变化快慢的物理量的时候,他指的是变化的快,而不是变化的大。一定要小心这样的一个概念描述。 嗯,也就是说,在这里面宿舍定义当中我们需要注意的第一个他的定义是怎样的?第二个最基本的公式以及所对应的亮钢计算,第三个就是他的物理意义当中的快慢。 好,我们继续更多校内同步好客加资料,当应用商店搜索物理大师零元等你来解锁。
78物理大师 07:44
07:44 02:54查看AI文稿AI文稿
02:54查看AI文稿AI文稿平均速度和顺时速度看个常见的例子,百米比赛运动员十秒时间内跑完一百米,在这十秒的时间内,他的运动快慢是不一样的。通过公式 v 等于得上 x 除以得上 t 求得的速度等于十米每秒, 表示的是这十秒内的平均快慢程度,这个速度就称为平均速度,常用字母微上面加一横杠表示。 可见,平均速度只能粗略的描述物体在得得踢时间内的平均快慢程度,那么为了更加精确的描述物体的运动,可以把时间得得踢取得小一些, 估计从 t 到 t 加德尔梯的时间内快慢的差异也就小一些。德尔梯越小,描述就越精确。若使德尔梯小到趋于零时至连在这段德尔梯时间内的运动可以认为是匀速的。此时,用公式算得的平均速度的数值就可以认为 完全精确的描述出了物体在时刻踢或者说在这个位置的速度,这个速度就叫做顺时速度。写成这样,所以顺时速度可以认为是智联在某时刻前后极为小时间间隔或某位置附近极为小位以内的平均速度。 当质量做匀速直线运动时,时时刻刻的顺时速度都保持不变,也就意味着在整个运动过程中,任何一段时间内的平均速度与任何一个时刻的顺时速度都相等。 当质点做变速实线运动时,每个时刻的运动情况可能都不相同,因此质点的顺时速度可能都不相同。如果要求平均速度,则必须指明是哪段时间内或哪段位移上的平均速度。在不同时间内或不同位移上的平均速度一般不同。 在以后的叙述中,速度一次有时指平均速度,有时指顺时速度,需要根据上下文来判断。例如,一辆汽车 从静止加速到二十米每秒的速度需要五秒,总共前进了五十米,那么二十米每秒就是汽车在第五秒末达到的速度,是顺时速度。在整个五秒的加速时间内,汽车的平均速度大小就是 v 八,等于五十米除以五秒等于十米每秒。 而汽车仪表盘上的速度计毒素,比如五十千米美食表示的就是顺时速度大小。这里需要提醒你,平均速度和顺时速度都是适量,满足时量的所有特点,既有大小又有方向。 平均速度的方向是致电在对应时间内位移的方向,而顺时速度的方向与物体经过该位置的运动方向相同。 如果是虚圈运动,顺时速度的方向是轨迹上霉点的切线方向。例如,将一个小球从 a 点抛到地面上 b 点,整个过程平均速度的方向由 a 指向 b, 但在空中任意点时的顺时速度方向就是个点的切 线方向。好了,总结一下,这一次我就给你讲了平均速度和顺时速度的概念。平均速度是用来粗略的描述物体在一段时间内或一段位移的运动快慢,而顺时速度可以用来精确描述物体在某一时刻或某一位置的运动快慢。 平均速度公示中,当德尔体趋于零时,平均速度就是顺时速度。平均速度和顺时速度都是适量,都理解了吗?
1011物理马老师 03:20查看AI文稿AI文稿
03:20查看AI文稿AI文稿大家好,我是爱物理的大侄子,今天分享两分钟理解加速度的定义。 加速度是指速度的变化量与发生这一变化所用时间之比。第一式是灯塔 v 比灯塔 t。 注意,加速度是由笔直法定义的物理量,与灯塔 v 或灯塔 t, 这两者均无关,只与他们的笔直有关。 v 一表示出速度,是指灯塔梯开始时的速度。 v 二指过速度,是指灯塔梯结束时的速度。加速度是用来描述物体速度变化快 慢的物理量,在国际单位之中,他的单位是米每二次方秒。加速度也可以称为速度的变化率。 变化率是指某量大地的变化量灯塔地与发生这个变化所用时间灯塔梯的比值。变化率的物理意义是描述某量地的变化快慢, 不表示某量地的变化量灯塔地的大小。在实际学习中,如果大地代为速度 v, 那么这个笔直灯塔 v 比灯塔 t 就是速度的变化率, 也就是加速度的定义式。所以我们说加速度是速度的变化率,和速度一样,加速度也是史料,它的大小可以由定义式来求, 大小就是定义式所求结果的绝对值。加速度的方向是与速度变化量灯塔 v 方向相同。 一起来看例题,关于加速度的说法,正确的是 a 选项。速度是描述物体运动快慢的物理量,而加速度则是描述物体速度变化快慢的物理量。 a 选项错误, b 选项。 加速度的定义式是 dota b 比 dottle t, 但它不是决定式。加速度的大小是由核外力和质量决定的,与 dott v 和 dott 无关,只与他们的比值有关。必选项错误。 c 选项,加速度是使量,使量前的正负表示方向,绝对值才表示大小, 所以负五米每二次方秒的大小是大于三米每二次方秒的。新选项错误。 d 选项,物体以四米每二次方秒的加速度加速就是任意一秒内末速度比出速度大四米每秒。 这里我们可以简单计算一下,由 a 等于灯塔 b 比灯塔 t, 我们可以得到灯塔 b 应该等于 a 乘灯塔 t 带入数据,会得到四 米每二次方秒乘以一秒,这样呢是四米每秒,说明任意一秒内末速度确实比出速度大四米每秒。 选项正确。这样这道题就解决了。如果大家喜欢我的视频,欢迎大家关注我,咱们下个视频再见。
105爱物理的大哲子 00:34查看AI文稿AI文稿
00:34查看AI文稿AI文稿哈喽,同学们好!今天我们要来学习一个新的概念,它叫做速读。在物理学中, 路程与时间之比就叫做速度。通常我们用符号 v 表示速度,用 s 表示路程,用 t 表示时间。那么根据定义,我们可以得出速度的定义公式 v 等于 s 除以 t。 也就是速度等于路程除以时间。你记住了吗?
49一舟 02:23查看AI文稿AI文稿
02:23查看AI文稿AI文稿高中物理第四课适量标量之前,我们学习了位移和路程速度和速率。我们把位移速度这种既有大小又有方向的物理量称为史量,而路程速率这种只有大小没有方向的物理量是标量。 在表示使量时,我们可以先射正方向,比如射向右为正方向。如果物体向左运动方向与正方向相反,则为复制。所以,如果位移是负五米,表示向左运动五米。 那么问题来了,负五米和三米哪个位移更大呢?大家可按下暂停思考做答案,答案将在三秒倒计时结束后公布。 与数学中比较数值大小不同,使量的符号仅表示与所设正方向相反,所以负五米比三米的位移更大。在比较使量大小时值比较 的绝对值。类似的,如果物体速度是负五米每秒,也比三米每秒更大。以下是拓展内容,基础不好的同学无需掌握。 钻石量和标量是用有误方向区分。实际上,二者主要的差异在于运算法则上。小学我们就知道三加四等于七,这个就是标量的运算法则,而质量运算则不同。以位移为例,一个人先向要走了三米, 右向上走了四米。位移是由初始位置指向末位置的有向线段。根据勾股定理,总位移是五米,所以使量三加四并不一定等于七。不过,如果先向右运动三米,继续向右运动四米,总位移是七米。 如果先向右三米,后向左四米,总位移又变成了一米,方向不同会导致不同的结果。之后我们会具体学习质量运算法则。最后一个思考题, 请大家思考电流是食量还是标量,大家可按下暂停思考做答案,答案将在三秒倒计时结束后公布。 电流虽然有方向,但是是标量,比如三安培电流和四安培电流交汇,无论方向如何,最终的总电流是七安培, 满足标量运算法则,所以是标量。因此判断标志量不单只看有无方向,需要根据运算法则判断, 大家现在不太理解,没关系,这里只是做个铺垫,后面选了史料预算法则大家就清晰了。以上就是本节课的内容,是不是很简单,如果你喜欢本课程,欢迎点赞关注,感谢大家支持,我们下节课再见大家见哦!拜拜!
7733物理云学习逸迭Eddie 03:05查看AI文稿AI文稿
03:05查看AI文稿AI文稿大家好,我是爱物理的打折子,今天分享两分钟,明确加速度与速度、速度变化量的区别。首先看速度与加速度的区别, 速度是描述物体运动快慢的物理量,他等于位移与时间的比值。而加速度是描述速度变化快慢的物理量,他等于速度变化量与时间的比值。加速度不能反应物体运动的快慢。 加速度为零,说明物体速度不变化,但速度不一定为零,物体可能以一定的速度做匀速运动。接下来看速度变化量与 加速度的区别。加速度是速度的变化率,而不是速度的变化量。加速度表示速度变化的快慢,而不是速度变化的多少。加速度不仅与速度变化量有关,还与时间有关。 加速度与速度变化量无直接关系,不能直接判断大小关系。下面以五个常见交通工具的实际数据为例,从直观的数据上判断加速度与速度变化量的关系。 对于火车出站,他的速度变化量很大,但加速度很小,所以速度变化量大,加速度不一定大。对于自行车下坡, 他的加速度大,但他的速度变化量却并不是最大的,所以我们说加速度大,速度变化量不一定大。结论是加速度与速度变化量没有必然联系。 下面通过数据直观描述加速度与速度的关系。飞机匀速飞行的速度是最大的,但加速度却为零,说明速度大,加速度不一定大。 自行车下坡,加速度最大,但速度却不是最大的,说明加速度大,速度不一定大。 加速度为零时,对应飞机匀速飞行,这时速度并不为零,而对于公交 车出站、线体出航、火车出站这些情况,出速度为零时,加速度并不为零,所以速度为零时,加速度可以不为零。结论,加速度大小与速度大小没有必然联系, 下面通过点力检测下,小伙伴们是否掌握了关于加速度的说法中,正确的是 没错,答案就是 c 选项了。如果大家喜欢我的视频,欢迎大家关注我,咱们下个视频再见!
101爱物理的大哲子 04:56查看AI文稿AI文稿
04:56查看AI文稿AI文稿大家好,我是有料、有思想、有爱、有深度的范老师,欢迎大家来到我的高中物理系列课堂,今天这节课范老师想跟大家分享的内容是速度和速率的区别和联系, 那么速度和速率一字之差,他们有什么区别呢?请同学们看白板。一进入高一,我们开始学习运动学,运动学第一个接触的概念呢就是速度,速度用字母 v 来表示, 速度的定义是什么呢?微等于嘚特 x 除以嘚特 t, 其中的嘚特 x 表示的是位移,嘚的 t 表示的是时间。 接着速度是一个失量,速度的方向就是位移的方向,因为位移也是一个失量,这是速度。 那么什么是速率呢?速率通俗的说其实就是速度的大小,速度的大小就是速率,所以速率 我们可以理解为对速度取一个绝对值, 这样去理解也是可以的。那么我们就能够看到,速度它是一个失量,它是有大小有方向的物理量,而我们弹速率的时候,它是只有大小没有方向的,所以速率是一个标量。 之后对于速率我们还要知道这样的一个情况,就是速率。还有一种速率叫做平均速率。 平均速率和平均速度不是一码事,需要我们注意把它区分。 比如如果我们说平均速度,平均速度如何来计算啊?其实平均速度的计算是还是这个,还是上面的这个 v 等于 dirt x 除以 dirt t 平均速度它依然等于位移,除以时间, 而平均速率不是。平均速率是什么,平均速率他是 路程,除以时间,都是它 s 除以得的题,位移是失量,而路程是标量。路程 是标量,所以平均速率也是一个标量, 他们俩在大小上面并不见得是相等的。比如说一个制点,从 a、 d 运动到 b d、 a、 b 之间的距离呢,是一百米, 接着这个制点,他要从 b、 d 运动到了 c、 d、 b、 c 之间的距离呢,是二十五米。 那么在这个问题里,平均速度跟平均速率的计算方式就不一样,因为在这个问题里,他的位移 是多少啊?位移应该是七十五米,而他的路程 多少路程是一百二十五米,位移跟路程并不相等。从定义上说,位移是出位置到末位置引出来的一条有详线段,那么来看出位置在这 末位置在 c 点,从出位置到末位置引出一条有相线段,这有相线段的长度就是他位移的大小,那么 ac 之间的距离是七十五米, 而路程不是。路程的物理意义是运动轨迹的长度。那么来看他的运动轨迹先从 ad 走到 bd, 走过多长的距离啊?一百米 之后再从 b g 走到 cd, 又走了二十五米,所以它的路程是一百二十五米。因为路程跟位移并不像 相等,所以他的平均速率跟平均速度也一定不是相等的。好,以上就是今天这节课,范老师想跟大家分享的内容,速度和速率的区别和联系。 速度是一个适量,而速率是一个标量。速率实际上就是速度的大小,对于速率还需要我们掌握平均速率,平均速率和平均速度是不一样的,平均速率是路程除以时间,而平均速度呢是位移除以时间。 平均速率也是标量,而平均速度呢,是适量。好,今天这节课我们就上到这里,感谢大家的观看,我们下次课再见。
 27:29
27:29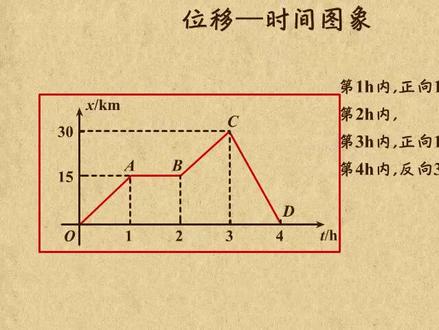 03:50查看AI文稿AI文稿
03:50查看AI文稿AI文稿这个视频我来给你讲讲位移时间图像。先从最简单的说起,一个制点做匀速直线运动,那就可以沿着直线运动的方向建立直线做表器,确定做表器的各要素,并将其化成纵轴。 但是直线坐标系中只包含支点位置位移信息,并没有时间信息。为了能在一个途中同时表示出时间的信息,我们可以用横轴表示时间,踢 横轴与纵轴的焦点哦,表示所要研究运动的初始点,既是规定的位移零点,也是时间零点。这样我们就得到了一个位移时间坐标系。在这个直角坐标系中所做的图就是位移时间图像,简称 xt 图。 若制点从初始位置欧出发做匀速直线运动,通过记录不同时刻制点的卫衣得到一系列数据。根据数据在 xt 图上描点,用直线将点连起来,则 xt 图是一条过圆点的倾斜直线。在数学上,过圆点的直线表达是为 y 等于 kx, 其中 k 是一个比例系数, k 等于 ybx。 k 越小,画出来的直线看起来越平缓。当 k 等于零时,直线与 x 轴重合。 k 越大,画出来的直线看起来越清晰。当 k 等于无穷大时,直线与 y 轴重合,因此给 k 一个名字叫斜绿。 在咱们的 x t 图像中,直线的斜率就是速度, v 等于 x 比 t 斜率的大小表示速度大小,越倾斜表示速度越大。比如这样,绿线表示的速度大于红线表示的速度。斜率的正负表示速度的方向与规定方向相同还是相反。比如这样,黄线 表示质点运动,沿 x 轴复向,初始时刻位于 x 等于四百米处,二十秒时刻回到规定的位移零点处。 如果红线表示假指点的运动 x t 图,黄线表示已指点的运动 x t 图把他们画到同一个图中,两线的焦点就表示甲和乙制点的相遇,即在 t 等于十秒时,他们在 s 等于两百米处相遇。 如果在计时开始时刻,物体的出位置不在位于零点,则 x t 图像就不过原点了。例如汽车运动以 x 零等于一百米处为初始时刻位置,那么 x t 图就是这样的, 写出位移时间公式, x 等于 x 零加 v t。 可见图中的斜率照样表示速度。如果 x 一图像是这样的,表示计时开始后,物体一直处于出位置五秒,然后以图像斜率为速度 v 做 匀速直线运动。如果 x t 图像是这样这样或这样的,因为图中斜地为零,表示速度为零,所以表示支点一直处于初始位置,保持静止。 看下面这个汽车做直线运动的 s 一图,从图中我们就可以看到,第一个小时内,汽车向正方向以十五千米美食的速度匀速行驶。第二个小时内,汽车静止不动。第三个小时内,汽车又向正方向以十五千米美食的速度匀速行驶。 第四个小时内,汽车向反方向以三十千米为时的速度匀速行驶,刚好回到出发点。上面的 x t 图像都是由直线上构成,那如果 x t 图像是曲线的话,速度又该怎么看呢?比如曲线上两数据点分别对应于直线运动中的 a 位置和 b 位置,曲线上这两个数据点的个线 斜率就表示从 a 运动到 b 的平均速度。当曲线上两个点无穷接近时,两点的割线就成了切线。因此,曲线上任意点的切线斜率自然就表示各个位置或对应的各个时刻的顺时速度。 好啦,总结一下这个视频我就跟你讲了,通过位移事件图像求出物体的速度。特别要注意的是, x 图像曲线并不是物体运动的轨迹图,物体真实轨迹是在 x 轴上的直线运动。都清楚了吗?快刷题去吧!
235物理部落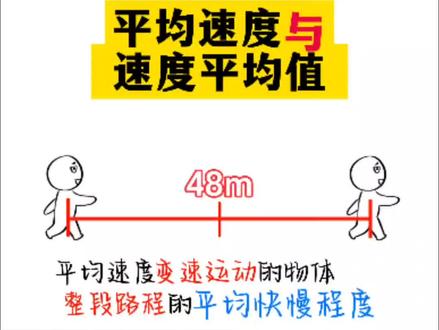 00:40查看AI文稿AI文稿
00:40查看AI文稿AI文稿一分钟学物理,平均速度不是速度平均值你知道吗?假设你做直线运动,全程四十八米, 前一半路程你用了四秒钟,后一半路程你用了六秒钟,那全程的平均速度是多少呢?你该不会是这样算的吧? 用两段路程的距离除以他们各自的时间,算出来了平均速度,然后求出平均值,这可大错特错喽! 平均速度是用来表示做变速运动的物体在一整段路程上的平均快慢程度,所以要用一整段路程上的距离除以他所用的时间,这样算出来的速度才是正确的平均速度。简洁物理,用最简洁的方法学物理。
861简杰物理
猜你喜欢
- 1068黑暗大臭

