粉丝96获赞368
相关视频
 09:18查看AI文稿AI文稿
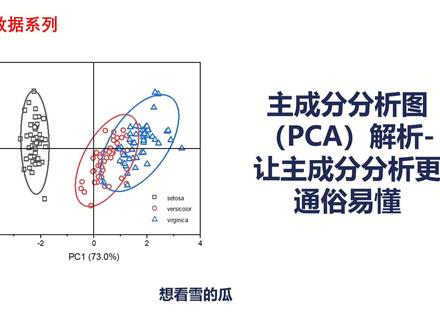
09:18查看AI文稿AI文稿各位小伙伴们大家好呀,我是想看雪的光,今天这期视频呢,是很多小伙伴想让我呃,就是更新的一期视频, 我最近也在查了相关的一个资料,然后也去看文献,然后看了很多视频,但是呢很多视频他讲的比较的一个复杂,然后我自自己也进行了一个梳理,然后想让这种 pca 图,然后更加通俗易懂,然后分享给大家 啊,左边呢,它这个图是它的一个 p c a 图的一个得分图,呃,这种得分图是怎么绘制呢?我们在之前的一个 一期视频当中也进行,呃,说明了,大家可以参考那期视频。然后首先呢,它是用 orange 进行一个绘制出来的嘛,然后我们 今天就不进行操作了,然后首先的话我们要看他,我这里有五组数据啊,不是七组 a, 这里有七组。然后我进行 pc 进行绘制,出来之后他出现了好几个图,一个是碎石图,一个是 啊在在贺图,一个得分图,一个整体的一个图。然后的话我们先看一下下面的 啊,那么什么是得分图呢?他是让门店在新坐标下的一个坐标,比如说这个啊,这个对应下来他是一点多,一点六,一点七, 就是这样看的一个坐标。然后那么特点呢,距离越近的一个样本间,他的一个相似度越高,由于我这个啊可能不太好说,比说 他这几个,其实他差相似度相差挺大的,也说明他们有很大的一个显著性。 我们再看一下前面的这个张图,比如说我们把这个黑色弄成一,然后这个红色是二,然后这个蓝色是三,他一和二他具有显著性的,然后一和三也是具有显著性的,但是二和三他是相似度很高的,但是他没有显著性, 就是这样一个特征点。然后第二个呢?呃,所有样本点在某个坐标轴组成份上的一个方差,等于组成该组成份对应的一个特征值 啊,就是比如说他这里他对应下来的一个特征值,就是这个 p c 一,他是,嗯,百分之七以上,然后这个是组成份方差,他是 是啊,百分之二十二点九,那这边他也是直接看他这个值的。另外呢,方差由大到小排序方差最大的,他是组成分 p c 一,然后以此类推,然后第二大的是 p c 二嘛,就是也是以此类推的。 然后我们看一下我们啊做,因为我刚刚也说了,我这个是有七个, 有七个组成分,然后我们该选择几个呢?一般的话我们是选择两个组成分,我们可以看他的一个碎石图,这碎石图出来之后 啊,我们可以看得到,一般比较大,我们选择的 p c 一, p c 二,就是这两个,然后它对应的一个翻差是多少呢?我们在这里它会给我们计算出来, 这个是百分之六四点一三啊,这个是百分之二十九点二四,一般的话我们就选择这两种就可以了。然后啊,因为我们在看我们线的时候,他最常见的是二尾的一个得分图嘛, 然后,嗯,如果你想计算一下某组成分的一个贡献率呢?他是用该组成分的方差除以所有组成分方差之和的。他这里的话也帮我们计算出来了,比如上面的话,他是啊,百分之六十四点一三,第一个组成分 p c 一, 然后如果你要算它的一个 p c 一跟 p c 二它之间的一个方差,它会这里是累加出来,呃,百分之九十三点三八,就是这样的,算它的一个某种成分的一个贡献率。然后那么什么是 债赫图?债赫图呢?他是主成分,是所有连锁变量的一个线性组合,债赫他是线性组合的一个系数,那么他的性质呢?在债赫图中,他越靠近的变量间正相关的一个系数越强。 然后 pca 中它通常采用的是皮尔性相关性。皮尔性相关性我之前用 spas 进行一个操作了,大家如果想用 spas 进行计算它的一个皮尔性的相关性也可以进行操作的。 这里怎么看他一个相关性?比如说我这里回复性、内具性、弹性,他们两,他们三个啊,就是差的很很小,然后几乎连在一起的,也说明他们一个相关性正相关性的一个系数很强, 估计已经达到一左右了吧,因为他们都快连在一起了。然后的话,你也可以看出来,比如跟他这些差的都很蛮大的, 也可以说明了比容跟他们之间的一个啊,相关性差的很大,但是有可能是互相关哦。 另外啊,我们如何以文献的一个图为例进行解析它呢?首先它这个,呃,文献,它是 我之前啊用那个金堵纹线的一个图了,他这个是对面包的一个笔溶,然后硬度、弹性、内具性、咀嚼性和回弹性进行一个组成分分析。他是探讨啊,当时我们是递进嘛,以他这周 这个面包的一个品质之间的一个关系。然后首先我们在这张图中,它这张图是在后图吗?我们应该怎么看它的一个图呢?比如说这里 p c 一,它是九十二点三七,然后这个是 p c 二 五点五三,然后我们就可以看出来,它这两个组成分,它占的一个总分差是百分之九十七点九零嘛。其中啊 p c 它代表是九十二点三七的一个差异性 啊,不是差异性,是变异性,他的这种变异性呢,他是以硬度、咀嚼性、内具性、回复性啊,成正相关的。这是怎么看的呢?比如说他这个组成分对应的一个坐标轴,左边是他的一个负数,然后右边是他的一个正数, 然后在这边一个正向线中,他是跟他的一个变异性成嗯正相关关系的啊,以此类推,他这个比容,他是以他的一个变异性是成负相关关系的。另外呢,你也可以以啊 p c 二为 啊,它的一个变异性是五点五三,它这里呢,它是跟比绒、回复性、内具性、弹性、咀嚼性都是呈正相关的,它是与印度呈负相关的,这个基本上它是啊这样看出来的一个整体的图。 当然你也可以从这张图中可以看出来,我们刚刚也说了,他可能是以回复性、内具性、弹性成一个很强烈的一个正相关的一个关系啊。具体你要啊,如果要计算他一个相关信息数的话, 可能还要进行一个用 spa 进行处理,他一个相关性的一个系数才能说明问题。另外我们再看第二张图,第二张图呢,他是一个得分图,他这个得分图呢,其实也跟我们刚刚前面介绍的其实差不多的 相比相比在成分一中他的一个这三个蓝色的,蓝色、黑色、红色,他是在啊成分一中的一个负向线中,然后的话他这两个是啊正向线, 也可以说明了他的一个很好的一个问题。还有看他一个成分二,他这个是正正向线,这个负向线啊,我们在 我们之前处理的一个数据为说明问题,比如说他这里是得分图,你这里也处理的一个数据出来了,但是他没有说明的他的一个问题。然后我们换一下啊,这个 整体一个图吧,然后它这里也出来了对应的一个坐标,可以看出来它这个 p c 一,然后这个是 p c 二,然后比如说它这边 b 对应的是多少多少, i 对应的是多少多少,这种的一个得分图, 整体的一个内容基本就这么多了,他这个解析啊,从这组成分分析中也只能看得到这么些。 好的,今天的内容就这么多了,大家有什么问题可以在评论区进行一个回复,我看到也会进行一个解析,我们一起学习。好的,拜拜。
2766想看雪的瓜 00:50查看AI文稿AI文稿
00:50查看AI文稿AI文稿这种图大家肯定都在文献里看到过,看着高大上,其实做起来非常的简单,他就是 pca 主成分分析,今天我就带大家简单操作一下。他的原理很简单,只要你有两组数据就可以进行, 他的目的就是为了将这两组数据之间的差异量化出来。举个例子,我这有第一组和第二组的数据,分别有年龄、身高、体重和鞋码的数据,我这里只是假设只有三个人,但实际上是可以无限制的。那我现在就将数据导入 呈现出来的图的意思就是这两组之间有差异,其中年龄因素导致了百分之九十四点五九的差异。我们可以看到呈现出来的图非常的直观, 是不是比你直接列数据要高大上的多呢?大家只要带入自己的专业实验数据即可,像实验啊,调查问卷啊,统计啊,文科理科都适用,你学会了吗?这里是正在读博的大语学长,关注我,带你开心读研!
2.2万大禹学长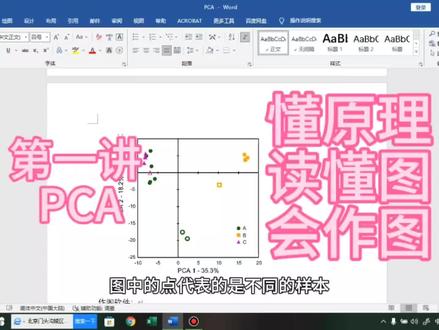 01:30查看AI文稿AI文稿
01:30查看AI文稿AI文稿pca 分析呢,又叫做主成分分析,它主要是,嗯将这个组成的复杂数据信息进行降为排序。但是呢,它有一个局限性就是,嗯, pca 分析是基于这个线性模型的 啊。那举个例子,比如说大部分的细菌都有一个生长最适温度范围,超过这个范围后,细菌的生长就会受到抑制。因此呢,这个 pc 分析就不再适用于物种风度变化范围大或者环境梯度变化大的样本中 啊。接下来我们说一下这个图,就是这个 pca 分析呢,主要是以散电图的形式来展现,图中的点代表的是不同的样本,然后不同的颜色形状又代表不同的分组。同组样本的远近说明了样本的重复性强弱。不同组的 样本的远近呢,则反映的是他们组建群落的差异性。那他这个图中的横轴呢,代表的是第一组成分,而纵轴代表的是第二组成分。两个轴上所标注的这个百分比就是该组成分对样品的 oto 数据的差异的贡献度。 通常来说,这个横轴都会比纵轴的这个数值会大一些。然后再说说具体我们用什么可以做这个 pca 的图 r 语言, canno, 还有还有各种网络平台都是可以做的。如果推荐的话,我肯定是推荐这种网络平台,因为它真的超级简单。
 05:03查看AI文稿AI文稿
05:03查看AI文稿AI文稿那昨天给大家介绍了主成分分析,也叫做 pc principle component analysis, 那它的横坐标是成分一,纵坐标是成分二, 也就是说我的横坐标这百分之七十六点八,我指的是我的成分一可以解释的我的变量百分之七十六点八五的差异,那比成分二可以解释百分之四点四六的差异, 那这个图叫做得分图,每一个点代表的是一个样本点,那这个正方形代表的是 每一个正方形的小点,代表组一的一个样本点。三角形的是组二的一个样本点,一个三角形代表一个样本点二,一个正方形代表一个样本点一。 他是用来看样本天然的分组情况,在分析时不添加任何分组信息,告诉这个软件我的所有点默认都是一个大组的,那图中每一个点代表一个样本点。 样本在空间所处的位置由其中所含有的代谢物的差异决定,也就是说这点离得越远,代表的是他们的代谢物的差异更显著,离得越近代表的是差异几乎为零,也就是代谢物的信息相似的。 那右边这个图就是载赫图,这个每一个点就和刚才的得分图是不一样的,得分图是每一个点代表一个样本,这个每一个点代表的是一个代谢物, 代表的是一个保留时间对应的纸鹤笔,其实就是一个代谢物,他是用来寻找差异的代谢物的变量。 距离远点越远的代谢物被认为对样本的分类贡献越大,也就是说越接近于四个角落的点对应的代谢物,越能解释他们组建的参议, 那刚才说的 pca 昨天介绍了,它是一种无监督也叫非监督的一种模型方法,模型拟合,那有监督的模型呢,就要 opsda 或者是 psda。 psda 又叫做偏最小二乘分别分析,那他对应的横坐坐标虽然也是成分一乘分二,但是他就不用 pc 一 pc 二来表示了,而又用 t 一 t 二来表示。右边呢,是 psda 对应的载合图,每一个点也代表的是一个化合物,一个代谢物 散步在角落,角落的点就更能解释足间差异。 区别在于和 prsda 的得分图,载和图和 pca 的得分图。在和图的区别在于, psda 在分析时提前赋予每个样本分组信息。简单的来说就是我告诉 我这个软件在模型礼盒的时候,哪些点是 a 组,哪些点是 b 组,在分析时扩大组间的差异, 减少阻内的差异,用来寻找我的标记物。那 ops d a 呢?他就没有载荷图,没有载荷图了,没有右边这个图了。但是他是有得分图的得分图, 他的横坐标是 t 一,动作标呢,就不是 t 二了,是另外一个变量,是他的意义和解释是一样的。那下面呢,就是 s plot 图,在 ops d a 分析中寻找标记物,通常使用 s plot 就不是用载赫图了, 那这个 s plow, 它的形状像一个大写的 s, 如图所示。在得分图中,两组样本分布在外轴两侧,通过 s plow 就可以获 的标记物在两组中相对含量的变化。也就是说,处在 spods 右上角的化合物离远点越远,对分类贡献越大。我在得分图 所对应的处在得分图外轴右侧的样本中含量较高,那布于这个 splo 的左下角呢?离远点越远,那他对分类贡献越大,那他就是对得分图外轴左侧的样本含量较高, 就是说左下角的点离远点越远, 对应着得分足外轴右侧的样本中含量越低,那对应的外轴左侧的样本含量越高。
115药物分析文献精读 00:50查看AI文稿AI文稿
00:50查看AI文稿AI文稿大家好,今天小编带你一分钟了解 pca 图。 pca 图怎么看主要是反映样本间的差异,当样本聚集在一起,说明样本间差异较小。当样本和样本距离较远,说明样本间差异较大。 pca 图的原理主要是将复杂事情简单化,通过将为映射现行变化来寻找一个方差最大和误差最小的最新变量。表征原始数据特征。 如果把图一中蓝色圆点看成是杂乱无章的原始数据,我们需要画一条黑线穿过蓝色圆点,蓝色圆点映射到黑线上变成红点。黑线可以不从角度旋转,当黑线旋转到 红色圆点,在黑线上的变化范围最大。同时蓝色圆点到黑线上的垂直距离最小时,即为我们所要寻找的方差最大和误差最小的最新变量,也就是 pc 主成分慢。为代谢为您提供领先的代谢组学技术服务。
106学术华仔 04:12查看AI文稿AI文稿
04:12查看AI文稿AI文稿如何使用啊进行主成分分析并可实化主成分分析的结果?在上一期的视频中,我们介绍了剧烈分析,它可以将观测纸分为若干个组,本质上是对观测纸进行降为。 在这期视频中,我们所要介绍的主成分分析实际上是对变量进行降位,其主要目的是创造少数几个相互镇交的主成分来表示原始数据中的数值变量所蕴含的大部分信息。 首先我们加载 tediverse 和 factor extra 这两个包,然后加载自带的数据及 mt cars。 这是一份关于多款汽车的设计与性能的数据。 接下来我们需要对数据进行预数。里使用 mutant 函数将属于分类变量的 vs 和 am 转换为自负串变量。使用 selective 函数和 is numeric 函数从数据集中挑选出所有数字变量。 下面使用 pr com 函数执行主成分分析。在这里我们将 santa 和点 scale 参数设置为处,其目的是中心化和规划所有数值变量,从而平等地考虑各个数值变量的影响。 接下来我们逐一介绍主成分分析的结果。首先,直接运行批压抗盘数创建的对象可以得到各个主成分在所有变量上的载合值。载合值可以理解为创建 组成分时的各个变量的系数。以第一组成分为例,使用中心化和规划的变量构建的第一组成分与各个变量之间的关系如下面的公式所示,其他组成分与变量之间的关系与之类似。 然后使用萨姆瑞函数获取各个主成分的重要性及主成分的方差占比与累计占比。可以看到第一主成分的方差占比为零点六二八四。第二主成分的方差占比为零点二三一三。 第三组成分的方差占比为零点零五六零,这意味着第一组成分表达了原数据中的百分之六十二点八四的信息,第二组成分表达了原数据中的百分之二十三点一三的信息。第三组成分表达了原数据 中的百分之五点六零的信息。另外,我们还可以看到组成分的方差累计占比及前两个组成分的方差累计占比为零点八五九八。前三个组成分的方差累计占比为零点九一五八, 这意味着前两个主成分或者前三个主成分解释了原数据的百分之八十以上的信息,这是选择主成分个数的一种标准。接下来使用 squee plot 函数绘制碎石图,可视化各个主成分的重要性。 可以看到图中的曲线在 pc 等于三之后基本不再下降,即 pc 等于三是一个拐点。一般来说,主成分分析降为确定的为数就是拐点对应的主成分个数。 最后使用 fact to extra 包中的多个函数可视化组成分分析的结果,使用 fvspcaind 函数可视化所有个体在第一组成分和第二组成分下的分布。 使用 fviz pca vr 函数可是画所有变量在第一组成分和第二组成分下的载合。使用 fviz pc byplot 函数可视画所有个体和变量的双标图。 以上就是对主成分分析在啊语言中的使用介绍,下期想学习什么在评论区中告诉我,期待您的点赞和收藏,祝您早安、午安、晚安。
159好伙计 16:34查看AI文稿AI文稿
16:34查看AI文稿AI文稿那么好,同学们,我们这一讲呢,讲一下 p c a 组成成分分析,这个 p c a 组成成分分析啊,网上有非常非常多的这个教程讲解,都讲的非常让人头皮发麻,非常晦涩难懂,我呢以一个图 去讲解一下,那么我这次以一个数据,就是这个数据,这是一个测序的数据工作标,这些是 每一个病人的名字,纵坐标呢,是他的测序数据各种基因,我们那个因为那个 t c j 数据库,他下载比较大,我就是复制粘贴了多少,粘贴了几百行啊。我们进行 一个简单的 pca 组成成分的讲解,以及他作图数据分析的结果的解读,相信这一定是全网最通俗易懂的一个讲解啊,希望各位能听完我的讲解以后啊, 非常明白, p c a 组成成分分析,到底这是是个什么东西? p c a 组成成分分析到底是什么东西,以及它出现的结果,我们如何解读它?那么好, p c a 组成成分分析,它一般就出一个这个图, 这种图在放在文章中,呃,就可以直接用在文章中进行发表,那么你看不同的颜色代表不同的组群,这每一个点就是一个人横坐标,这是 dam 一啊,这是储主成成分分析的成分一,这个是成分二。 当然我们在分析主主成成分分析的时候,我们可能会用非常非常多的成分去分析他,但是这个二维图啊,只能显示两个坐标,横坐标和纵坐标,三维图呢,可以显示 x、 y、 z 三个坐标轴的数据。四维图目前不太好做,让大家更直观的看这个结果。 p c a 主人成问分析啊,它就是一个降低数据维度的一种统计学方法 啊。我们可以明显看出来,我们以横坐标一个维度,纵坐标一个维度,把这些人啊进行了分群,分成三个群,主要分成三个群,这一群呀和这个群呀离得很远,证明他们俩之间呀 有非常明显的不同。而这个群啊,黄色的群和这个红色群啊,也有部分的这个重叠啊,所以说他们之间到底有没有意义了,还并在分析降为啊,这,这里头我们需要提出一个 关键词,什么叫降维?好,我以一个具体的实力讲解一下什么叫降维。大家来观察这个 excel, 这个数据,地震,这是病人一,这是病人二,这是病人三,这是病人四, 他测序完了以后,他身上有五百多个标签啊,测了五百多个基因的表达量,但是你说我们如何使少量的数据来代表这个人呢? 我们是用这个蛋白呢?还是用这个蛋白呢?还是其他的某些蛋白呢?不,这都不,不太可能,不太现实。我, 我们只有把这些不同的蛋白,依据他的具体表达量的数据 进行一个浓缩,以一个非常非常少的数据维度来代表这个人,这个数据。降维所产生的降维维度一、维度二、维度三、维度四,可能也有很多维度, 他并不是一个具体的蛋白的表达量,而是根据这些所有的蛋白的表达量,通过统计些计算算出来的一个具体的数值, 那么我们就可以把它降低维度了。我现在演示一下如何进行 p c a 组成成分分析,等我演示完以后,我们根据的图进行一个简单的解释,相信你看完这个视频以后啊,会非常明白 p c a 组成成分分析是个什么 作用。我们把每一个病人通过他基因测序的维度啊,你看,假如说我们在这个看完第一个病人,那么他有多少个基因的含量呢?五百八十五个,去除第一行是五百八十四个这一个病人呀, 一个病人通过五百八十四个基因蛋白的表达量,也就是说五百八十四个维度确定了这一个病人。但是如果我们在现实生活中,通过统一学计算以及图片展示的过程中,我们不可能展示出一个五百维的数据 啊,因此我们需要把这个病人啊,降成有限的维度中啊,到底降成几维呢?因为现在统一些软件啊,他可以计算三维的吧,也可以计算四维的维度,他是可以计算,但是就是说 在图片展示的过程中,它就不太好计算。假如说我们展示成啊, p c a 成分一, pca 成分二, pca 成分三啊,这是一个具体的数值,我们拿着一个 pca 的成分呀, pc 主要成分成分一,成分二,成分三,这三个数据去非常能代表它,那么我们的降维从五百多维降到了三维,那么降到三维以后呀,我们是不是 就可以进行更良好的计算了呢?它呀,这个 pc 主要成分成分一呀,它不特指这些基因里的一个蛋白, 而是什么呀,而是通过这些蛋白经过一系列的运算,最后得到一个数值。理解了这个概念以后啊,我们进行一个组成成分分析的演示。 好,这是他的基因蛋白,请详细看我现在的操作和演示啊,这非常重要,我们必须 点中第一行,我们选中最后一行的最后一个数据,按着 shift 放手,是选择一个框,而不是 ctrl 加 a 全选。然后我们复制 新建一个 excel, 命名为 p c a 三, 打开。好,我们呢,在这个 excel 里,它有一个功能叫转制点,这, 这个转制,我们把它变成纵向坐标,那么这样看来,横着的是,这是一个病人,这是一个病人啊,这,这竖着是每一个病人,而他横坐标呢,是各种基因蛋白的 数据测取数据。好,我们在这右键插入一行,我们把它命名为组别 group。 啊,我就在这底下就,呃,因为这是 t c g a 数据库嘛,有一些是肿瘤啊,一些是正常人。呃,这是我随便定义的啊, 他,他并不是,就是说他确实是这样。好,我们把这个维度定好。好,我们把这行删除,把他的名字删除啊,这是我们做好的数据,我们进行保存,关闭,我们打开我们的软件 are reading, 具体这个软件怎么安装啊?网上也有一些详细的教程,我们把它关掉,这个地方,点数据导入, 我这里头。呃,导入了很多了啊,大家可以把这个点,这个添加和删除,把这边的东西啊,都按这个箭头都导到这边,然后他就所有的这种数据类型都可以导入到。啊,这是弄了。好,我们点导入,从文件中导入, 我们导入哪个呀? excel 点选桌面,把这个地方呀,选择二零零七年以后的版本,我们导入 pca, 主人身份证三点添加确定, 那这个地方不用先不用管它啊,点确定,我们这样呢就把它导进去了。我们需要把这一行呀, ctrl x 扔到这个地方啊,这是 group, 我们进行,我们用一个插件儿啊, p c a 主人成分分析的这个插件儿啊,点击 input data, 我们点 前线, 一共有五百多行,耐心选完。 好,我们,我们我们从第二行到一百八十八行, group 呢?是第一行, 这样点这 settings, 把这些能打上的勾啊,咱给它打上。这个地方可以画一个三地图,也可以画两地图,你看三地图了,就是把 组成成分三啊二,一都给写上。如果我们打二地图呢,他就只选两个啊, 这个是 output。 这个地方我们不点啊, 我们我们先画一个二地图啊,点, ok, 好,现在他开始进行了组成成分的运算以及他的结果。好,我们现在有组成成分四十八个组成成分,这个四十八个组成成分是怎么看的? 组成成分一,他呀,可以把这个他算,他具体算出来一个值啊。 嗯,组成成分一啊,他有百分之二十七的代表性啊。组成成分二呢,有百分之十二点一的代表性。组成成分三呢,有七的代表性。 如果说我们用三个维度去描述一个人的情况下,那么我们有百分之四十七的可能性,怎么样呀? 准确的预测他啊,这个因为他这个矩阵量太大了,所以说,所以说他一共有四十八个维度啊,四十八个维度,这个到百分之百啊,他就过你和了啊,他就不太对,我们在四十六个维度,如果我们用四十六个维度 啊去描述一个人的情况下,那么他可以达到百分之九十九点八三 的这个符合率,也就是描述性啊。嗯?什么意思呢?我们输入的数据,我们输入的数据 是五百多个蛋白啊,五百多个蛋白,然而呢,我们进行 p c a。 主任成为分解以后,我们把这五百多个蛋白啊, 浓缩成了四十七个维度,去同样的描述这个人啊,到底这四十七个维度分别是什么呢? 啊?这个点,这个地方啊,他会他给你把这个,呃,每一个蛋白啊,每一个蛋白,一共五百多个蛋白啊,五百多个蛋白怎么样?算了,一个什么呀?平均数加上啊,标准差, 这个地方我们没有点,我们没有选择这个 observation 啊,选择了 observation 的情况下,我们就可以看见了啊,这也选了,你看,因为咱们到了四十七、四十八个维度的时候,你看它四五、四十九、五十,它因为它百分之百过你核了,所以说它们就不过去了,对吧? 然后你看四十八个维度里这些呀,就是他的这个维度的评分啊,维度的评分,每一个基因对于他维度的这个评分 啊,这个,呃,这个是画图的时候所需要用的这个东西啊,画图的时候所需要用的。好,我们继续在这看,我们都把它打开,这是各种的不同的图,这个是总图啊,我们首先看第一张,双击 好,这个图出来了,因为我们有四十八个维度啊,四十八个维度,那么这里头这个方块啊,它应该有四十八个方块,每一个维度啊,它的这个权重是多少?第一个维度 p c a。 一 comment 的权重啊,就是就是,非常高,然后越来越低,越来越低。 如果我们用一个维度、两个维度、三个维度,那么我们可以预测到百分之四十多啊,百分之四十七点多,对刚才每一个病人的一个代表性,这个图片也是可以导出去的啊,右键给他导出去,就是第一个图啊, 第二个图咱们一般不用啊, a few moments later 第一张图啊,这是一个点,两个点,这一共呀,根据啊,刚才咱们看的那个表格啊, 他应该是有四十多个点啊,四十四十八个点,也就是四十八个点,他第一个点啊,是 pc compament 的一,第一个维度,他第一个维度啊,非常非常的强大,前三个维度啊,就已经占到了百分之四十六的预测率啊, 比如说按照这三个数据,按照前三个维度的最终算出来这个指标啊,就可以预测,预测每一个,或者是代表每一个病人。这个图,这个图是什么意思呢? 这里头啊,他的箭头啊,箭头顶上啊,都有一个蛋白啊,箭头顶上都有一个蛋白,因为咱们这个蛋白太多了,就是说每一个蛋白啊,他往哪个方向去走 啊?这里头一共有五百多个纬度啊,五百多个箭头。这比如说,我举一个例子吧,比如说这个这个蛋白 n c l 这个蛋白他能看清啊,他在 p c a 组成成分的 company 管的。二、第二个第二个 维度的时候,它是一个负相关的相相关性,你看它是负数,当然啊,它在这个 p c a 一这个维度中,它也是个负相关的 啊,也就说这个东西啊,他是跟这些维度是一个负相关的关系,同理这个象限是完全双正相关,这边呢是维度一正相关,但是呢维度二负相关。 好,这里头呀,每一个点啊,就是一个病人,这个圈啊是把它百分之九十五肯定期间,哎,我们可以把它 一到这缩小一些这个距离啊,这个图啊,直接就可以导出啊,或者说是截图放在咱们的文章中了啊,这就是这就是咱们这个 pca 图上分析的图,从这张图上我们可以看出什么呀?我发现组一和组二啊,他们俩混到一块了, 分不清啊,分不清楚,分不开,并不像咱们这张图一样分的很开啊,当然你的数据 有数据很好的情况下,他是可以分开的,分开了以后证明一件什么事啊?证明这两个群呀,两个群呀,可以根据他的成分,两个成分啊,这两个成分给他分开, 就是这个图和这个图合起来就是这个图,所以说我们一般在文章中放这个图。好,我们主要是会分析他的操作 以及他的解读,进行了一个比较详细的讲解啊,如果还有什么问题可以随时在视频下面留言啊,我会看情况给予大家回复,感谢观看!
53郭鹏 04:55查看AI文稿AI文稿
04:55查看AI文稿AI文稿各位老师大家好,我是麦维代谢的产品经理任胜景,今天给大家分享的是我们麦维云平台的第一个常用小工具,高级 pca 分析。 我们都知道代谢主角数据是高维且复杂的,所以需要通过多元统计分析方法,在最大程度保留他原始特点的基础上,对他进行简化和降维。而 pc 分析就是这样一种多元统计分析方法, 他通过中间变换,将一组可能存在相关性的变量转换为一组线性不相关的变量,那这个变量就叫做主成分。简单来讲呢, pc 就是通过将高维的代谢组学数据转化成 n 个主成分来描述原始 数据级的特征。对应到图中我们可以看到,横坐标 pc 一表示的就是能描述代谢数据矩阵当中最明显的特征。纵坐标 pc 二表示的就是除去 pc 一以外最显著的特征。 图中的每个点代表一个样本,不同的颜色代表了不同的分组。通过 pca 分析,我们可以了解各组样本间的总体代谢差异 以及组内样本之间的变异度大小。在本图中, a 组与 c 组间存在明显的分离趋势,也就表明这两组样本当中的代谢物存在着较为明显的差异。 ok, 接下来我们就来看一下具体的操作步骤。 呃,下面现在 大家介绍高级 pc 这个工具的使用说明。首先打开这个工具啊,左边蓝是填写参数上传文件的蓝,右边是包括工具介绍、详细说明以及常见问题等描述文本 啊,我们要做的是填写这些参数啊,上传相应的文件,点击提交按钮,然后我们的任务就可以开始分析了,而这些参数文件填写的规范在详细说明里都有十分详细的描述,比如 第一个参数,任务名称,这个参数是用于多任务管理的,建议长度小于二十个字符啊。第二个参数,输出文件名称,这个参数控制分析完成后的 zoo 包文件名 啊,注意,这个参数禁止使用中文字符,特殊字符很下划线啊。下面一个参数是输入表格文件,您可以点击视力数据这个按钮,将这个文件下载到本机, 点击打开,可以看到我们的视力文件是什么样的啊。同时在咱们的详细说明里也有对这个文件的详细描述,大家可以根据这些描述对自己的文件进行更改后上传文件。 而样本分组文件是对这个输入表格文件进行分组的啊,这个文件只有两列,而第一列的内容是 第一行,呃,是上面这个输入表格文件的第一行,而古鲁普就是对这些呃样本进行分组的。 要注意的是,这两个文件都应该是啊, txt 格式的,以太补为分格负责文本文件编码,建议大家都使用 utf 杠八这个编码,其他格式的文件是暂不支持的啊。最后一个参数,会议化参数,我们 提供了出会 fos 两个选项啊,这个表,这个参数表示在进行 pca 分析之前,是否对每一行每个代谢物数据进行一位违规规划。 点击提交按钮后,这个任务就进入了工具列表,工具任务的列表啊,我们可以点击查看,看看一看这个工具的分析 结果啊,大家可以看到这个图就是刚才以单位数据提交后的结果,可以点击齿轮按钮对这个图片进行个性化微调。比如我们输入一个标题,大家可以看到这里就出现了相应的标题,同时我们可以对字体字高 x 轴标题、外轴标题进行相应的修改。当然我们可以控制显示是否显示图例,是否显示标签 在外观尺寸。这个菜单可以控制咱们这个绘制图形的宽度和高度,以及符号的大小,符号的形状。 三格样式可以对这个图形的背景进行相应的控制。呃,在修改完后,点击下载按钮就可以下载相应格式的图片。如果您对这个图片还是不满意,您可以点击编辑 svj 这个按钮进进入在线 svj 编辑, 可以对这个图进行更为啊详细的调调节。
23学术华仔 02:22查看AI文稿AI文稿
02:22查看AI文稿AI文稿今天我们来看一下数据处理方法,成分分析。成分分析是一种利用数学降维的方法,利用政交变换, 把一系列可能线性相关的数量变转化为一组线性不相关的新变量,也称为主成分, 从而利用新变量在更小的维度下展示数据的特性。主成分是原有变量的线性组合, 其目数不多于原始变量组合之后相当于我们获得了一批新的观测数据,这些数据的含义不同于原有数据, 但包含了之前数据的大部分特性,有着较低的维度,便于进一步的分析。如图,唯我们得到 的主成分分析图。那么如何绘制这个主成分分析图呢?我们来看一下。我们来到网页,这里推荐鼠小弟网站,网站为 ww 点科研 d app 点 com。 我们来到鼠小弟这里, 我们点击绘图工具有一个,这里需要上传两组数据,第一个是我们的原始数据库,第二个为数据的标注。我们来看一下数据格式, 如图为数据 c 一到 c 六, a 一到 a 六, b 一到 b 六。我们将数据分为三组,同时对数据进行标注,从 c 一到 c 六, a 一到 a 六, b 一到 b, 第六进行了标注。我们现在上传我们的数据库,如果你也喜欢玩这个游戏,数据库上完成,完成以后,我们点击提交得到任务编号, 在这里粘贴回车。我们的分析已完成,请及时下载。点击下载之后,我们打开文件夹,这里有 pdf 格式、 图片格式和网页格式,我们选择 pdf 格式来查看一下,这样就得到了我们一个主成份缝隙图,供大家学习参考,谢谢大家。
26子兰论文社 07:14436萤火虫科研
07:14436萤火虫科研






