粉丝2010获赞2.0万
相关视频
 02:14
02:14 02:33
02:33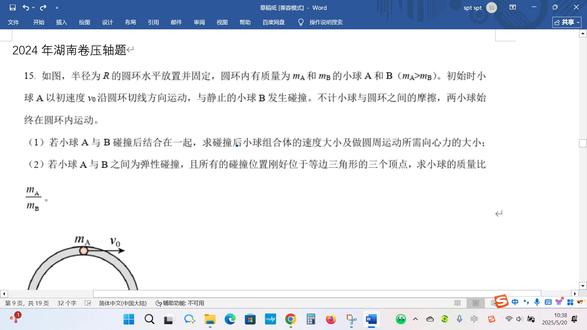 37:08
37:08 00:12查看AI文稿AI文稿
00:12查看AI文稿AI文稿我建议不要去做这么难的题,这个好像就跟物理竞赛似的,这种东西对小孩的这个自信心的打击太大了,要不要把好奇心给熄灭了?人一好奇心一熄灭,人就变笨了。
8889湖南广电金鹰955 00:11
00:11 02:28
02:28 10:11
10:11 10:14查看AI文稿AI文稿
10:14查看AI文稿AI文稿我们再来看到今年湖南卷的亚洲题,这道亚洲题的模型是非常简单的人传模型,但是他的第二问和第三问的分析是非常需要观察能力和一定的数学基础的,所以确实有一点难度要求同学们对这个数据比较敏感,而且运算能力要比较强。我们我们首先来看到第一问, 首先是水平方向动量守恒,所以就有 m v x。 我们设小球的水平速度为 v x 减去大 m v v 是大 m 的速度,就等于零,这是第一个公式。 然后再根据能量守恒,运动到最低一点的时候, m g b 就等于二分之一 m v x 的平方加上二分之一大 m v 的平方, 这是第二个公式。由此可以解出, v x 等于根号下两倍大 m g b 除以大 m 加小 m。 而要我们求的那个 v, 它就等于根号下 二 m 的平方, j b 除以大 m 括号大 m 加小 m, 这是那个速度的求法。然后位移,你只要对一式取速度均值,是不是就有 m v x 平均减去大 m v 平均等于零?好,同乘以一个时间 t 就可以得到 m x 小 m x 小 m 指的是小球在水平方上的位移, 就可以等于大 m x 大 m, 这是第三个公式。再加上这里面的位移关系, x 小 m 运动到最低点的时候,它加上 x 大 m 就等于 a。 第四个公式 连立后就可以得人穿模型的二级结论, x 大 m 等于大 m 加小 m, 分之小 m 乘以 a。 所以这一问其实真的还是比较好做的,绝大部分同学都能够拿到分。接下来呢,我们再看到这道题的第二问,这道题的第二问确实是比较有难度的, 首先一点是我们怎么去找这里面的几何关系,而且你要把它表示成坐标 x 的形式,所以为了方便分析呢,我们把图再画一下,假设这个圆弧槽往右 边运动了一段, 这节运动了一个 x 大 m, 那么它所对应的这个椭圆的中心是不是也往右边运动了一段,这个 x 大 m, 然后一样小球掉下来, 这个时候小球所处的位置,我们设它水平方向上的位移为 x 小 m, 然后这会儿它的坐标你要把它表示成 x 的形式,就是这一段的长度,这个是 x, 所以这里面的几何关系,首先能够观察到的一个是这个 x m, 这个 x 和 x 小 m, 它们两个的和是等于 a 的,把它写出来 x 小 m 加上 x 等于 a, 相当于是第五式。接下来我们还能得到的几何关系是什么呢?就是第二问,里面人传模型的一些基础的知识,就是 x 小 m 比上 x 大 m, 它跟质量成反比,它得等于大 m, 比上小 m 就是第六式 好做到这里呢,可能很多同学就卡住了,接下来这个轨迹方程怎么找呢?是不是?所以你得能够注意到什么呢?你得能够注意到一个细节, 无论小球和这个凹槽怎么动,这个小球是不是一直在凹槽上面的,也就是如果我去观察运动过程当中的这个紫色的图,小球所处的位置,他始终要满足一个跟凹槽构成的椭圆关系, 这个椭圆的中心有变化,变化到了这里来,所以很关键的一点就是你要把这个点的坐标表示出来,就是我们刚刚设的 x 大 m, 那么既然是椭圆的话,它是不是就可以满足这样的规律?就是 x 减去 x 小 m, 它的平方比上 a 的平方加上 y 的平方除以 b 的平方等于一。这就是很关键的。第七个方程,也是卡住很多同学的这个方程,它其实就相当于是坐标原点移动的一个 xm 的距离。 刚刚我们的这个 x 是 x 大 m, 嗯,好,那你接 下来是不是只要把五和六的结果带到下面这个方程来就可以了?来连力就可以写成 x 减去大 m 分之小 m, x 小 m 的平方除以 a 的平方加上 y 的平方除以 b 等于一。把 x 小 m 也带进来,结果就是 a 的平方分之 x 减去 大 m 分之小 m, a 减 x 的平方加上 b 的平方分之 y 的平方等于一。后面呢?哎,我觉得可以不用再花减,基本上做出这个结果应该这一份,应该这一万的分呢就能够拿到了。再来看到第三万,这个第三万可以说是非常的刁, 如果他不是这样一个关系,那我们根本就不知道怎么做,而恰好他就是这样一个关系,你一定要把这个关系利用好。怎么利用呢?你先把他带到第二问的方程当中去,将 大 m 比上小 m 等于 b 除以 a 减 b, 代入二中,就可以得到 x 减去 b 分之 a 减 b 倒过来了, a 减 x 的平方除以 a 的平方加上 y 的平方除以 b 的平方等于一,这相当于是第八个方程。 好,那做到这里呢?可能又卡住了,接下来怎么做?所以这里 实际上就是考察我们的观察能力和数学计算能力了,在还没有结果之前,你要接着往下分析,就可以得到一些比较巧合性的东西。继续往下算嘛, a 的平方分之一,那 x 零出来,加上 b 分之 a 减 b, x 减掉 b 分之 a, a 减 b, 括号 的平方加上 y 的平方除以 b 的平方等于一。接着化解 a 的平方分之一, 然后这边剩下一个 a, x 后面还有 a, a 减 b 除以 b 的平方,加上 y 的平方除以 b 的平方等于一。 好,做到这里,其实差不多就可以发现了,这里有个 a, 这里有个 a, 然后外面还有个平方,可以跟这个 a 的平方给它消掉。那结果就变成什么呢? b 分之 x 减去 a 减 b 的平方, 加上 b 的平方,分之 y 的平方等于一。那后面是不是很明显啊?其实就是 x 减去 a 减 b 的平方,加上 y 的平方等于 b 的平方,这是不是就是一个圆的方程? 圆心在哪里呢?圆心在 a 减 b 零这个位置,半径呢? r 是不是就等于 b? 所以它的轨迹 其实就是一个圆周运动,圆形的坐标是 a 减 b, 然后他现在告诉你下落的高度,这一段下落的这节高度是等于二分之 b, 既然他的轨迹是圆,那他的速度是不是就 沿切线方向?这就是它的 v 跟竖直方向所乘的夹角,我们设它为 c 塔,在这里设一个角度, c 塔,首先就能够得到 三 a, c 塔等于二分之一, c 塔角等于三十度。好之后,剩下的问题是不是就回归到了基础的动量守恒和能量守恒的问题了?你知道了下路高度,又知道了速度方向,那我们就可以列出,首先是能量守恒, m g 乘以二分之 b 等于二分之一 m v 的平方,再加上二分之一。好,我们把它跟前面区别一下,设成小 m 小 m, 大 m v 大 m 的平方。 这个是第九个公式了。再列一个水平方向,动量手横,那就是 m v 小 m 水平方向的速度 set 减去 大 m v 大 m 等于零。好,这是第十个方程,接下来解这两个方程就行了,只不过再提醒一点,这两个方程解出来的结果,你不要忘记 要把这个东西带进来,结果不能保留大 m 和小 m。 最后经过一系列的计算啊, 可以得出来,这个 v 小 m, 它可以等于二 b, 根号下 j 除以 a 加上三 b。 以上呢,就是这道压轴题的讲解。
1418教物理的的小龙老师 11:11
11:11
猜你喜欢
- 1354☞磊哥☜
最新视频
- 3.2万龙坚英语








