2022届全国乙卷数学有多难
粉丝4.4万获赞175.0万
相关视频
 11:57查看AI文稿AI文稿
11:57查看AI文稿AI文稿二零二二全国语卷导述这个压轴题啊,这道题目的话呢,是一道变态的分类讨论题啊,让很多同学非常绝望啊,做完这道题很多同学充分能够认可啊,数学确实是上帝的语言,而你并非那个信徒是吧,那我们今天的话给大家化解这种绝望啊。 看这道题啊,第一道题,呃,这个第一问非常简单不说了啊。第二问是说这个函数的话呢,在负一到零,零到正无权上各自有一个零点啊,求 a 的这个取值范围好吧,呃那我们正常这种题的话呢,你 零点马上等于零啊,然后等于零,我们会想的是把这个一的负 s 方乘过来哈,就变成说一的 s 方乘以这个 lone 的这个 s 加一啊啊,他等于 a x 这样子一个情况, 这类似于餐面分离啊,当然你就不要把 s 再出过去, s 出过去非常非常费劲是吧,你不出过去其实这个都都不好研究哈啊,然后我们餐面分离这样去尝试完之后发现是极其难搞的啊,这个指数跟我们的对数纠缠对 在一起,非常的研究啊,行不通啊。所以我们这道棋并不是这个餐面分离啊,我们是研究这个原函数吧,那原函数那基本上就是讨论的吗?对吧?你要求导啊,我们把这个导师求一下,这是我们取完导师的一个情况啊,然后这道题的话,接下来就研究这个导航式的一个正负吗?哈决定的原函数的这个增减啊。 呃在研究之前的话呢,我们建议要先看下这个函数啊,大概是什么情况啊,就你要找他是这个零点对吧?你让他等于零哈,你要看一下有没有一些特殊的点,特殊的值啊,比如说你看他等于零, s 等于几,他会等于零呢?有没有呢啊?你要稍微看一看啊,因为 很多导师题我们都会有一些巧合在的啊,一些特殊的纸,比如说你会带谁吗?你看你定义遇负一道零,那么肯定会带这个 f 零啊, f 一啊,或者说 f 一啊这种的算一算是吧,像这道题的话,他实际上是有一个特殊的纸,就是 f 零啊,等等,上一个零也是他 过远点啊,哎,这个还是非常好的,再过这个远点,过这个远点的话呢,我们要找的是他在这个负一到零上,就还有一个零点在这啊,在这还有一个零点,好吧,就我们能不能把这个图稍微勾勒一下呢?其实上是可以的啊,比如说你看这个,他整个是由分子的正负啊,就决定整个式子的正负, 那么如果 s 是趋向一正无穷的时候,这一坨是正无穷吗?这个的话,不论 a 是正是负哈,他的只永远会比 es 肯定是要小一些,所以整个市值的未来的话,一定趋向一正无穷,对吧?这这个就是趋向一个正数啊, 所以再 s 去向于正无穷,他一定是个增函数啊,这这个 fx 啊,所以你的图像,你看你过远点,在这又有零点的话,那你要么是这种情况吗?要么你是这种情况吗?对吧?根据我们刚才的分析,只能是这样子的吗?你是真的吗?在 s 去向于正无穷的时候,所以我们就可以把这个图像大致画画出来啊,那负一道零怎么画呢?负一道零 是这样的啊,是根据函数这种,呃,顺畅性啊,平滑性,像这种函数他肯定是平滑的,他不会是那种突兀的出来,对吧?所以你看你这样子的话,这边你这边肯定是这样子的呀,对吧?就他不太可能是这种情况,明白吧?啊?这是当然,我们是大概画一下啊,至于说后来他具体怎么样,我们呃 随着分类讨论进行再去这个确定,好吧,所以这是我们大概的一个图像啊,可以对于我们的这个思路的分析啊,会有所这个帮助的啊,那么接下来可以讨论啊,讨论什么东西呢?首先主要这个地方有 a 哈,这个地方有 a, 其实 a 决定的这个开口朝向,你是不是要讨论一下 a 是正还是负,是吧? 还有同学情况比较简单的,比如说你看这个地方啊,如果 s 负一到零,那这个就是正数,而如果 a 也是正数,整个分子就是正数,他可能就是约还是增了,对吧?我们可以先讨论下简单的啊,作为突破,所以我们先写一下啊,就 我们这种情况下的话,可以得到 f 是真的啊,那真的可不可以呢?啊?就是根据这个图,你看他这个 f 零点零,这个非常重要,对吧?那他如果是真就这样这个图像了,显得就没有里面,所以就不行了,对吧? 其实我们的一个这种情况下,好吧。啊,那么我们还有一种,就是如果 a 等于零呢啊,那 a 等于零的话,其实这个地方就是零,那这个他永远就是增的了,你也可以用这种情况来排除他,是吧?所以 a 等于零,我们可以归纳的第一种情况来啊,那这就是第一种情况啊,然后我们再讨论的时候是第二种情况,是 a 小 a 零的时候,好吧, 哎,小林说我们要研究的是这个分母啊,这个就其实不是很好研究,我们的话呢,就是这个假设一个函数啊,就这个,对这个分子啊, 我们设为 gx 啊,我们来研究他哈,研究他的话呢,这个地方我们呃一般情况再去个岛,你感觉其实就是二阶岛,对吧?啊?一俩四方减去二 ax 啊,这个 二街道好不好研究呢?这个二街道 a 是副的哈,你看,如果说 s 是正的情况,他比较好研究,因为这样他就是大一点的。哎,他这个 gs 是个增函数,对吧?所以我们先研究这种情况啊,这种情况下就是 gs 是个增了哈, gs 是增的话呢,其实我们可以把 gs 图像画出来啊, 那 gs 是增,其实并不是我的目的,我的目的是要研究 gs 的正负,对吧?那他有些什么情况呢?哎,他是增,他增的话,他最小就是机灵的时候啊,如果机灵都大于零,那整个就 gs 大于零,他就那,那原函数就是个增函数,原函数增函数的话,你看是这个样子,显然是不行的,对不对? 所以的话呢,我们说这个呃机灵啊,就机灵,你算出来机灵是否大于零,这个很关键啊,如果是他大于等于零的时候,也即使说的话呢,你看 a 的话呢,是这个大于等于这个负一啊,小于零的时候,那我们的 gs 到就会大于等于机灵吗?这个时候他就是个正能, gs 是大于零,零的话就是这个分母是分子,是大于这个等于零的,好吧,那这样的话呢, fpx 就会大于零, fp 的大零 fx 就是个增函数,增函数和刚才讲,你看你这样话是不行的,没有零点的,对吧?那所以的话呢,这个时候 fx 就会大于这个 f 零二, f 零等于零,你看又用到 f 零零零非常重要的一个条件啊, 所以 a 大于等于负一小,而你是不行的啊,但是我们在 a 小于是又细分了一个,你看为什么到这一步的哈,这个很重要这个思路啊,那我们接下来就做 a 小于负一的时候啊, a 小于负一的时候的话,我们可以把这个 gs 啊,就是你,呃,我们画一个这个适宜图啊,当然这个是一个草本上的啊,我就不再画草本上,我直接画到这里来了哈, 就我们画这个 gx gs, 大家看他是应该是这样子增函数吗?这是 gx 啊,这个时候的话呢,你会发现这个地方是一个机灵吗?哈?他是小一零的吗?啊?那他的话就会有一个是什么?你看这个 ga 就是先负后正,对于原数来讲的话,就是什么情况呢? 啊?就是先减后增,对吧?其实就是这这样一个感觉啊,那我们就是现在的话要找到这个零点,好吧,这个零点的话,实际上来讲,由于这个 gs 当时含有 a 的嘛,时尚是不好找的,但是我们可以找他的范围啊,所以我们这个这个零点他 比零要大一点,我们再带一些纸哈,比如说比零大,你会带谁呢?我们带 g 一, g 一的话也算是一还是大一点的哈,所以大家看这里面其实会存在一个 s 一这个零点啊,所以我们就是说啊,会存在一个这个 x 一哈,它是属于谁的呢?属于零到一的啊,然后能够使得什么?能够使得 gx 一是等于零的, 那这样的话,大家看就是在这个 s 属于零到 x 一这一段来讲的话呢,哎,我们 gx 来讲就是一个附属啊, 那我们这样的话呢, fpx 就会是个复数啊,然后你就可以得到说 fx 就是一个简数啊,那我们同样的话呢,如果说 s 属于是 x 属于 s 一到这个正物群的时候,他就反过来是增函数了啊,其实就是在描述的图像是先这样子再这样子啊,你都可以把这个什么呢 x 一给他标上去啊,这就是 x 一了,其实 这是我们描述完图像了,我们还要这个叙述出来,说他在这个领导政务局上,哎,确实会有一个这个零点,好吧,那我们怎么去叙述这个事情呢?哎,那你在这一段他肯定是负的,所以你把这个这个地方 fs 一线算出来,他肯定小 f 零吗?这是个复制, 你再找一个正直哈,这这个地方你看是一个增函数吗?我们再找一个正的出来,根据零点存在定理,他就会有个零点啊,当然这个其实是不好找的啊,非常非常费功夫,所以我们就不再去找某一个值了,我们去找这个正无穷,当然是去年正无穷的时候,他属于 这个正无穷,就是这么一个叙述方式。好吧,我们接下来把这个过程写一下啊,大家可以看到这个图啊,就是 fx 一肯定是个副手啊,然后我们再写一个,就是当 s 区相于谁的呢?正无穷的时候啊, fx 的话呢,显然是驱寒于正物群的啊,这个的话呢,自己可以轻松的判判断一下啊,所以我们这个 fs 正出来的话,他在这个 s 一到正物群上一定会有一个零点。好吧,那我们接下来再研究这个负一到零啊,负一到零是最变态的啊。呃,因为负一到零的话,这个二一是个负的吗? 沉到一起是正的啊,你看正数减正数,可正可负啊,他不像刚才那么简单,对吧?刚才的话,你看这个 gps 也是大一点的啊,这现在他有正有负了啊,所以这个时候怎么搞呢?比较复杂哈,我们的思路是这样子的,你要记清楚,就是我们需要先把它研究清楚 再去研究它啊,只要 gs 研究清楚了, fs 也研究清楚。好吧,所以你先研究它,不要乱掉了啊。这个其实就是二阶倒,而这个二阶倒的话,大家可以看得出来哈,你这个 a 是一个小 a 零的数啊。呃,这样的话呢,一的 s 方是个增函数,负二 ax 一次的嘛,啊,那也是个增函数嘛,因为 a 是负的嘛,所以这整个它是个增函数, 所以我们可以把这个 gps 画出来哈,当然这个草本上的分析哈,就是写过程不要写出来就可以了。我这里的话直接给你写出来了啊,他的话呢,你看他应该是一个这个增函数,增函数我们先这样随意画一下啊,比如说是这个样子啊, 那么我们也得研究这个东西的正负,再决定他的一个证件,好吧,所以的话他正负,你看这曾涵说啊,你还是负一到零,你肯定要算一下负一和零的值吗?对吧?当我们一算的话,发现这个基负一是这个,这个的话呢,二 a, 你 a 是小于一个负一的哈,所以这个他小于负二的吗?这个才二点多分之一吗?他这肯定肯定是小于零嘛,对吧? 然后的话,我们这个机灵的话是一啊,是大于零的啊,所以的话呢,其实我们这里的话呢,你要把它画准确一点,还是这样一个感觉啊, 呃,注意哈,这个是 gps 哈, gps 是这种感觉哈, gps 的话呢,是增函数,然后有一段是负的,有一段是正的啊,那么我们 这个地方这个零点也很重要啊,所以我们给他这个假设出来,这个假设 x 二的话,好吧, x 二肯定是负一到零之间的哈,这样 gps 研究清楚了哈,我们画一个小横杠哈,断开来哈,要不然会乱掉啊,我们接下来的话呢,去研究这个,呃, gxgs 就是一个,什么情况?他就是一个吸烟 减后增的啊,然后你这个地方你看就是 x 二,明白吧?啊,我们 gps 先负后正啊, ga, 呃,这个 gs 是先减后增,好吧,呃,大家别忘了,我们最终是要研究下的啊,我们最终是要研究这个 gx 的一个正负的, gs 的正负决定的原因是这个增减性,所以接下来我们也需要求几个,对吧?因为你 s 是负一到零的哈,所以我们也需要求一些什么,比如说基一和这个 肌肤一盒机灵啊,刚才这个地方少了一个皮啊,肌皮啊,所以我们看到的话呢,这个 机负一是一个正处机零的话是个负数啊,所以他应该是这样一个感觉啊,就是你把这个什么呢? s 轴的话呢,如果说画出来的话啊,就是我们看到的话呢,这个 gx 而言的话,你会发现,你看啊,但是这一段是个正的啊,这一段话是个负的,哎,也就是说 gx 的话呢,在负一到零上是一个先正后负, 那原函数的话呢,就应该是先增后减,其实就是谁啊?就是我们刚才描绘这个,你看先增后减,哎,这不就可以吗?刚刚好吗?然后剩下你把这过程描述一下,洗一下就可以了啊。 啊,我们的话呢,假设说哈这个地方是一个 s 三的话啊,然后 s 三的话呢,你看肯定是什么样啊,就是我们 s 三存在哈,它是属于谁的呢?属于负一到 x 二之间啊, x 二,当然之前你们你要描述一下, x 二的话,属于这个是负一到零之间的,这是存在的,对吧?能够使得啥呢?这个 s 三的话呢,我们说是使得这个 gx 三的话呢,相是等于零的,对吧? 我们的话呢,当 s 属于负一到三的时候啊,然后 gs 的话会是一个带领的啊,就是 fps 带领 sf 是真的哈,其实就是说,呃,在这个图当中啊,你看这个图像当中就是这啊,这是 s 三。好吧,我们叙述的就是这个这个部分啊,接下来我们再把这个部分描述出来啊,一样的哈,我们就直接写了。好吧, 那我们接下来的话呢,只需要描述一下这个就是这段他有个零点啊,描述一段还差不多啊,你写一写 fx 三,你看是个正数啊,然后再写一些,当然是需要一负一的,是负无穷啊,这样话你看是不是就有零点,对吧? 我们写出 fs 三哈,他是大于这个 f 零的啊,那么当 s 趋向于这个负一的时候, fs 肯定是趋向于负无穷的哈,所以的话我们就得到时候 fs 的话,在这个负一到零上的话呢,他就会有一个零点啊, 这样的话,其实综上来讲 a 是不是就需要一副就可以了啊?这道题是极其变态复杂的一个,这个讨论啊,对逻辑的这种缜密要求非常非常严格啊,你的话呢,建议下去的话呢,先自己 做一遍,不行的话再看,他可能需要你反复看几遍啊。前面这个还是简单一点点,按大点数,还是是负一到零的时候,尤其是比较变态的啊,你看我们先研究的 gpx, 再研究的 gs 这个顺序 gs 之后再得到这个 fx 是这样一些一层一层的关系,好吧。
471孟见数学 25:06查看AI文稿AI文稿
25:06查看AI文稿AI文稿好,我们再看一下二零二二年全国高考已卷啊,二十一期,据说这道题也很难啊,这个考生反应啊,全国已卷出的也挺难啊,还有全国新高考遗卷啊,全国新高考遗卷我已经给同学们呃,讲了很多了啊,呃,基本就算讲完了啊, 那么今天呢,我们再看一下全国已卷啊,最后一道压轴听啊,呃,以致函数 fx 等于异味的 e 加 l 对出,加上 a s e 的负 s b e, 求 a 的意识,求取现 wif 在点名 f 零处的切线方式。疑问呢, 我们得到的结果是 y 等于二 x 啊,这个我就不给同学们说了啊,第二个,横着看,第二个,若函数 fx 在区间负一零, 开局间零到正不凶,开局间各下有一个零点七五 a 的取之范围。我们看这道题,我们应该怎么去思考这个问题啊? 那么你想一想,这韩束 f 在什么样的情况下,他在这两个开区间内各有一个零点的?我们首先对着函数图像的我们来,我们有一个大致的分析啊,首先呢,我们注意到 f 零点零,对吧?把零带去之后啊,是 f 零点零, 那么 f 零点零的话呢,那么图像他是经过原点对吧?经过原点以后呢?那么在什么样的情况下,他在这个区间和这个区间各有一个零点呢? 我们可以通过图像我们给他分析一下啊,我们看一下。那么而且 我们还看到当 x 趋向于正无穷的时候,这个函数 fx 应该是趋向于正无穷,这能看出来对吧?呃,这个是趋向于零了对吧? x 除以 e 的 x 是 m, 当 x 趋向正无穷的时候,我们用罗格达法则,我们发现这个趋向于零,这个趋向于正无穷。 而且当 x 的趋向负一的时候啊,因为他的有一条间接线呢,是 x 应该很低啊,那个 x 必须得会大,对吧?定义是大于规尿。那么当 x 趋向又负一的时候,这个是趋向某一个长数, 那么这个是趋向于富不穷。你看这个图像呢,经过原点,当孩子去向正不穷的时候呢,他趋向正不穷,当孩子去向富一的时候,他趋向于富不穷。而且我们还想让这个函数图像 在这两个区间上啊,各有一个啊?焦点,那你想一想,这个图像你说应该怎么画?那么这个图像我们是不是只能是应该是这个样子,那对吧?啊?错,应该是这个样子, 趋向正无穷啊,对吧?虚向正无穷,咱们这个图像应该什么样?应该是大概应该是这个样, 然后呢,我们看,对吧?他的图像啊,大致的走向啊,应该这样,那么只有这样的时候呢,我们才得到什么呢?得到这个函数 fx 啊,在这两个开局界内啊,各有一个零点, 那么如果是这样的话,那么我们很容易看到。那么就说这个函数啊,在负一段 上应该有一个机制点啊,在零到征求上也应该有一个机制点,对吧? 所以说呢,我们又猜想到什么问题呢?那就说这个函数的导函数,在负一人上应该有一个零点,在零到正无穷上也应该有一个零点啊,而且这是个电话零点。 因此呢,我们就围绕着这个函数的导函数啊,在什么样的情况下,在这两个区间上各有一个零点啊,从这个角度啊,我们来分析,然后我们对 a 进行讨论, 所以说呢,我们首先呢对函数 fx 呢,我们应该进行求导,对吧?那么求导以后呢,我们发现他是一加 x 分之一啊,再加上 a 在秤上啊 e 的负 x, 再解决 a 秤上 e 的负 x 密,然后呢,我们把它通下分啊,通下分之后呢,是 e 加上 f, 再秤上 e 的 x 密, 上面一个是啥?应该是 e 的 x 是 b, 再加上 a, 再乘上 a 减去 x 的胸框,对吧?由于呢分母是正的,是吧? x 大于灰机嘛, 所以说呢,我们要想考察这个导函数,在这两个区间上各有一个零点,我们只要看分子啊,这个函数就可以了,我们在令啊, u x 等于 e 的 x, b 再加上 a, 秤上一减去 x 平方,那么在这个函数啊,这个函数,我们定的这个函数呢,就是说 你能不能观察得到这个函数啊,在这两个区间上各有一个零点,如果这个函数在这两个区间上,在这个区间上,或者是在这个圈如果没有零点的话,那么 所确定的这个 a 肯定是不适合 t 啊,我们可以得到这样的猜一下, 那么在力所能及的观察的范围内,你能不能看出啊, a 在什么样的范围内,这个函数在这个区间上,或者是在这个区间上他没有零点呢?你能不能观察出来呢? 那么很显然你看,很显然,如果当 a 要是大于等于零的时候, x 在这个区间, s 在这个范围内的时候,那么他显然没有零点,这能不能看出来是吧? 那么 x 在负一到零这个范围的时候,那么他呢显然是大于零,恒成力, 如果他要是没有零点的话,那也就是说呢,导航数是吧?应该是大于防避,所以说导航数大于, 那就说 f x 呢,那就说在负一到零这个区域上应该得到,对的,所以说呢, f x 啊,那就横小于 f 零,而 f 零恰好对联, 这说明啊, f s 在负一到零这个区间上不可能有零点,当有大电影的时候,所以说呢,那么 a 大电影呢?应该是 这是啊,第一种情况呢,我们观察得到啊这么一个结论,那么首先我们再看第二种情况, 那么第二种情况呢,肯定就得 a 就得小于零了,对吧?当 a 小于零的时候,我们能不能看出这个函数在这个区间上或者是这个区间上没有零点呢? 如果大一小而零的话,大 s 在负一到零的范围内的时候,那么这个是个负的,这是个正点,一正一负相加,是吧?一正一负相加,这是有可能有了点,对吧?啊?有可能有了点,也可能没有点, 那么当然是在这个区间内的时候,那么这个呢,是有证有数,对吧?有证有数呢,那么现在也无法判断这个函数到底是有零点还是没有零点, 那么这个时候我们应该怎么办呢?我们应该呀,对于这个函数的增点性进行分析,这对吧?然后我们判断 s 在这两个区间当中的某类区间里,他有没有零点的问题,那么这个时候我们应该需要对这个函数求导,我们利用导数去分析一下, 那么取完枣之后呢,他是得这个,对吧?得这个呢?现在我们观察一下,观察一下,说这个函数啊, 呃,是导航,是不是他,那么当 a 小于零的时候,咱们这个导航是显然是单调递增,这能看出来,是吧?那么他要是单调递增的话,那么我们现在看,我们看哪个区间呢?我们可以看这个或者是这个,那么如果看这个区间的话,那么导航是单调, 那么这个导航数的职业应该小,把零带上之后,他应该小一,对吧?那么在在这个区域上导航数小一,那么小一呢,也可能小于零,所以说呢,这个导航数呢,在这个区域上可能是有证有负啊,那这样一来的话呢,那么呃,这个 这个函数呢,那时候在负一到零呢,可能有根点,对吧?那么我们再看看这个函这个区间,当 x 在零到正不穷这个范围内的时候,那就说 他不单到地灯了吗?我们就得到啥呢?我们就得到了,把零带下去之后呢,他正好得一,所以说把零带下去正好得一的话呢,那么当 s 大于零的时候,是吧? 当 s 大于的时候,这是在 s 大于的情况下啊,那么 大龄情况下,那么这个倒函数是正的,这说明啥呢?说明啊,这是 us 啊,在零到真无形这个区间上,应该是改造金增啊, 所以说呢,那么 ux 啊,就应该是大于啊,幽灵,那么把幽灵带上之后,我发现他正好等于一加上 a 啊,一加上 a, 那么做到这一步呢,我们很明显看到,如果当这个 us 的最小值要是大的那个人的话,那么 这个和数是吧?在零到真无雄这个区间上也是没有零点,对,对吧?所以说啊,当一加上 a 大于等于零,是吧?记, 当 a 大于等于负一小于零的时候,因为在 a 小的情况下,这十号这个时候呢,他的宝函数应该是大于零等于零,对吧? 所以说呢, f x, 嗯,在这个区间上,他应该看到底子,所以说呢, f x 那就大于 f 零, f 零的账号对人衡成立,所以说呀,当 a 啊,在这个范围内的时候, 那么也不满足条件,对吧?所以说呢,负一小于代理 a 小于这种情况,也应该把它舍掉。所以说呢,我们 经过分析讨论,我们发现啊,这个 a 有可能比负一小,那么这是第二种情况,我们再看一下第三种情况啊,第三种情况啊,当 a 小与负一的时候, 那么根据我们刚才的分析看,那么我们就考虑他的导函数,在负一人和领导政务权上各有一个零点啊,也就是说这个函数啊,各有一个零点, 我们是不是就可以得到这样一个结论呢?我们需要说明一下,当 a 小于负一的时候,那么这个倒函数显然是当 x 啊, 当 x 大于零的时候,那么这个导函数啊,显然是正,对吧?这个导函数正,那,所以说呢, 这个函数在零到正无穷这个区间上是单调递增的啊,又因为我们把它把零带去,把零带去之后呢,发现他等于是一加上 a, 当一小于负一的时候呢,那么这是比零小, 那么我们再带一个纸巾,我们带一个一进去啊,带了一进去之后,他正好等于一一呢,是比零大,你看,所以呃,存在 x 零在零到一,也就是零到正无形这个范围内的时候, 呃, us 零正好等于零啊,那么 us 零等于零呢,我们就得到啥呢?得到这个 x, 在 啊,零到 x 零这个范围内的时候,这个 ux 是小育人啊,也就是近 f 导数应该是小人啊。然后呢, x 在 x 零到正无穷这个范围内的时候,那么 ux 呢,应该是大一点啊,也就是记 他的导函数应该是大一点,所以 fx 在 零到 x 零这个范围内的时候,应该是单调递减,在 x 零到正中求这个区间的时候,是单调低温,对吧?呃,所以啊,这个 x f x, 那么根据这个图像看,又 fx 就说这个待到地点,那就说 f 零,对吧?应该是这个大于啊, f s 零,对吧?跟到地点吗?是吧?那么 f 零呢?正好可以零,是吧?记 f x 零是小于零,哎, 那么小于零的话呢?我们看,那就说明 fx 啊在零到 x 零这个范围内啊, 在零到 x 零这个范围内啊,是不可能有零点的,对吧?实际上这个 x 就是,呃,这个零,对吧?不可能有零点,那么我们再看,我们再验证一个问题,验证个啥呢?就说又因为 s 零没有变,那我们还验证谁呢?我们再找一下,就说是比 s 零大的,只是看看能不能找到这样一个点,对吧?找到这样一个点,那么我们看怎么去找这个点呢?我们可以通过极限的思想,实际上可以看出来,当 s 曲项正不行,是 s 曲项正不行, 但是呢,我们可以把这个点找到,这个怎么找?又因为用放错法,又因为 fx 等于 e 加上 x 啊,再加上 a 乘上 xe 到负 xb, 他显然应该是大于, 这个是不是比一小啊,对吧?这个比一小啊, x 除以一的 x 肯定是比一小了,他比一小呢?我称上一个 a, a 是个负的,对吧?所以说他, 他应该是大鱼,是不是应该大一盘这把放色,因为他比例小, 两边乘上 a, 他就应该是大于,然后呢,我利用他大于等于零,所以说我们可以得到 这个 x, 一加上 x 应该是大等于一的负 a 四 m, 所以说 x 应该是大等于一的负 a 四 m 再减去一,这个显然是比零小,他,对吧?他是不是比零小啊? 啊?比零大,比零大,因为 a 是负的,他显然是比零大,这个是比零大,那么他比零大呢?我们实际上就是找不到什么的,所以说就有 i e 的负 s 密,再减去一,他肯定是大一点,所以说呀, f x 在,嗯,零到正无穷上有归一的零点, 对吧?所以说当一小学负一的时候,我们已经正处 fs 在零到正中学上有唯一的零点。现在我们在证明,当一小的负一的时候,在负一到零这个区域上, f 也只有唯一的零点啊,就可以了。 呃,刚才的证明说,当 x 大于负一小于零的时候,我们在证明是 fx 在这个区域上有为零点啊。当 x 大于负一小于零的时候呢?那么这个导还是 数还是单调第三,对吧?我们可以把它看看导人数,把这个负一代去啊。导完数负一代去之后呢?他应该是等于什么呢?等于一的负一四方,是吧?然后再加上二 a 是吧? 再加上二位,那么一的负一的方加上二一啊,这个数显然是比零小啊,这个不用补数,因为 a 小就会移动,对吧?显然是比零小,那么我们再看, 再把这零带去啊,把零带去之后呢,他得一的零私密啊,可以一啊,这个是比较大,所以说啊,啊,存在微一,存在 s 一,在负一到零这个范围内,实则 这个导函数啊,因为导函数可以,所以说呢,这个导函数啊, 啊,这个档是吧?在,呃,在负一到 x 一这个范围内的成绩,他应该是为负,是吧? 然后呢,在 x 一到零这个范围,应该是为正,所以说呢, ux 在 负一到 x 一这个范围内,应该是单的递减,在 x 一到零这个期间上,应该是单的递增啊,所以说呢,这个 ux 应该是小 玉幽灵,看,对吧?而幽灵呢,我们看,应该等于什么呢?把幽灵带下去,应该是等于是一加 a, 是吧,一加 a 呢,应该是比零小,哎, 所以说啊,那么当 us 小于幽灵哈,那么 use 啊,是 us 一小幽灵啊, us 一小幽灵,那就说明啥嘛,说明是 us 在这个区间上啊,不可能有零点,对吧? 那我们再看这个啊,又因为又负一,把负一带去啊,把负一带去之后,他应该是等于一的,负一次命,他显然是比较大。 说一说,一定是存在 x 二啊,属于谁呢?属, 属于是负一到 x 一这个范围内,对吧?呃,负一到 x 一这个范围内,嗯,因为是负一大人嘛, s 一小人嘛,嗯,实得。 呃,十得啥呢?呃,十得 us 二半截这地方, 呃,所以啊, ux 啊,在负一到 x 一这个范围内,他应该是 啊,在 s 二反应不到 x 二的范围内,应该是为为证啊,为证。然后呢,是在 x 二啊,到零的 这块地应该是为酷啊,他图像啊,大概就是这样啊,你看啊是什么意思?就是这么个意思,哎,这是 uf 啊, 啊,这点呢,是 s 二啊,这个是 s 一啊,这个是零啊,出墙大卫这么个意思啊, 呃,那么我们再看,我们再看,呃,所以说呢,也就是说呀,导函数啊,在负一到 s 二的范围内,他应该是为证,对吧? 然后呢倒函数在这个区间上是破解, 所以说 fx 呢,在数一啊,一直到哪,从从数一一直到 呃, s 二,他应该是单到第三,对吧?然后呢是 s 二到零,他应该是单到第三, 呃,所以说呢, f x 二应该是大于一个 f 零,对吧? f m 四二 大于 f 零 f 零,这说明啊,说明啊, fl 在这个区间上不可能有零点,那么我们再验证一下,哎,就是这个 s 二是吧,这个就是 s 二, 那么 f x 二大于零呢?我们需要看大 s 趋向于负一的时候啊,这个函数 f 显然虚向于负重,但是我们找一点,这点怎么去找呢?我们就放作法,又因为 f x 啊,等于 加上 a 乘 f c e 的负 s d, 他应该是小于谁呢?他是小于,这个 他为什么小于?他在给我说明啥话呢?这个 x 乘上 e 的负 x 是密啊,我们在当 x 大于负一小二零的时候啊,他的最小值是负一,这个我们可以,嗯,驱动出来,他的最小值是负一的话呢, 那么 a 是负的,那说明他应该喜欢这个狮子啊,喜欢这个狮子,你可以求一下 s 乘以的负 s b 啊,他最小值负 e 啊,当 s 再负一个零这个范围内的时候,这样一来的话呢,那么我只要让他小月港里人就可以了, 小点名的话呢,我们起不来,那么这个 x, 那就是一加上 x 呢,应该是小于等于 e 呢? ea 四 m 啊,然后呢,我们把一移过来,那就是那叫啥,那就是 x 小于一趟啊, 这是 f 小点它,那么这个时候啊, fe 的 ea 次密再减去一,它正好是小一点,而且呢,这个数呢,显然是比零要小 九,对吧,因为 ea 是负的,对吧,显而比例小,所以说呢,这样哈,我们就找到啥呢?找到啊,就说是另外一个点,嗯,他比零小,所以说 fs 呢,在负一到零这个区间上也有 v 的顶点啊。 哎,这就是刚才啊,我把这个题啊啊进行了这个解析和讲解。呃,我的整体思路是这样,就说,首先呢,我们先对这个韩式的图像进行分析, 主要是抓住他过远点的特点,然后呢,我们再考察这个图像啊,当孩子去向正无穷,说去向正无穷,当孩子去向复习说他去向富无穷, 而且又经过原点,而且呢,这个行业图像,而且在这两个区间上各有一个焦点,那么这个时候呢,我复习成啥呢?这个行是导函数,在复习和联合和领导政府群众应该各有 一个变号零点,所以说呢,我们对他进行求导,然后呢,我围绕这个导栏数,在负一道联合零道正无穷这个圈上有无零点这个问题啊,对 a 进行分离讨论 啊,这就是我对这道题的解析啊,当然这个题是不是还有其他题的办法,你比如说能不能令他本野人分离常数啊?分离常数看可不可以,或者是 呃构造这个双函数啊,然后做叉再进行考虑。你得说的六大白眼睛是吧?六大白眼睛之后呢?然后两边称上一点 s 四 b, 这样的话呢?构造双人处,因为这是 as 嘛,他是表示一条直线。嗯,通过这个角度看看看能不能呃把这个问题解决啊。嗯,这个我也没有进行探讨,希望听众和同学们。嗯,有时间的时候呢,自己再研究一下啊。我的讲解仅供同学们参考。好。
189伯麟数学 07:44查看AI文稿AI文稿
07:44查看AI文稿AI文稿一卷第二十题啊,这是一个超级变态这项链巨大无比的一个圆队曲线题啊,如果你平时圆队曲线练的比较少, 计算能力比较弱,肌的同学啊,根本没戏。好吧,那我们看这道题啊,题目叙述比较简单啊,就是说一个椭圆啊,没告诉我们焦点在哪里啊,然后他过两个点啊,然后求一的方程 啊,这个的话呢,我们是一个基本功好吧,就是你可以设置一个方程啊,是 mx 方哈,加上一个 ny 方啊,由于不知道你的焦点是在 i 轴还是外轴,就这样是最稳妥,对吧? 然后将这个 a 和 b 的话呢,带入进去啊,比如说 a 带进去的话呢,你看啊,你会得到说四 n 等于一啊,然后这个 b 带进去啊,就是四分之九 m 啊,再加上一个 n 等于一个一,这个时候你可以求他 n 的值和 m 的值啊,然后因此可以写出来这个椭圆的方程,我们发现这个椭圆的方程的话,他焦点是在这 这个歪头上的啊,外放下面这个字要大一点啊,主要是看第二问啊,第二问的描述的话是在这个椭圆当中啊,你看他有点屁啊,这个屁的坐标什么情况?他中指标跟 a 是一样的啊,所以他是在椭圆外这么一个点啊,然后的话呢,他说是过 m 做一条直线啊,就是教这个椭圆与 mn 两点啊,这样做啊, 那么我们做出来之后也不知道谁是 mccn 呢,那他也没有说,那应该应该都是可以的,对吧?然后他说,呃,做完之后的话,什么情况呢?就是说又过 m 做一个平行于癌轴的一条直线啊,跟这个什么呢?跟直线 ab 会有一个焦点,是这个 t mt 等于 th, 那这不就意思是说这终点的意思吗?对吧?就这么一个情况,他们正的是啥?你看正的是说,哎,这个 hn 的话呢,经过一个定点啊,就这么个意思,这是我们这个图哈,大概画出来就这种感觉啊,有同事画这个图怎么这么难画啊,你只要有尺子,基本上就能画成 这种情况,好吧,这是把提议先树立好啊。嗯,那我我们怎么去这个想怎么去操作这件事情呢?你看全程他是这个直线,是由这个过批点这个决定的,对吧?我们肯定是说,哎,你看 mn 点坐标弄出来吧,哎,你直线肯定射出来两粒吧,对吧?然后的话呢,你看有 m 我们可以就可以知道 t, 有 t, 可以知道 h, 这样 h 点坐标可以用这个 m 点坐标来表示,哎,这样的话,你可以把这个 h n 这条直线写出来,来看他是不是过这个哪个定点啊?这是我们的一个思路,对吧?当然这个思路想的简单,但是你再去实际计算的时候,气散量会比较大, 但这个的话呢,又没有其他的一些特别好的一个想法啊,这是一个最直白的想法啊,唯一我们可能就是能够简化运算的啊,就是说这个定点能不能提前知道,是吧?怎么提前知道呢?哎,作重定点问题啊,我们得找一些特殊位置, 对吧?比如这条直线,你看你在做的时候,待会你要设直线方程的时候,哎,你是要问自己一下,他有没有斜率啊?因为我们可能要设 k 码,他有没有可能没有斜率呢?你看如果是这样子的话,这个 m, 这个是 n 的话, 哎,好像也是可以的啊,没有奖对不对?所以这就是特殊位置啊,哎,你把这个特殊位置写出来,然后我们再去找这个这个定点,看能不能找到。好吧,我们来先画一下这个图哈,我们也不知道谁是 m 谁是 n 的哈,假设上面就是 m 啊,下面就是 n 的话啊,随便标一下啊,这样的话你可以把这个 m n 点做,不要取出来, ab 直线也要取出来哈, 这是我们写出来这些啊,这样你可以选 t 啊,然后由于这个 t 的话呢,是 mh 终点,所以你可以去写出来这个 h 啊,我们可以把 h 点这边写出来之后,然后就可以写这个 hn 的一个直线了,这个的话大家自行写一下啊,当然他需要这个计算量啊,但是他是一个固定的一些运转啊,但是有个问题就是说你只知道这一一个固定的位置,一条直线他过两 定点呢啊,当然你可以去猜,但是这个东西的话呢,可能要靠灵感,对吧,或者说也不是很好猜,所以怎么办的呢?所以的话呢,我们可以这样子啊,你可以再找个特殊的位置啊,这个就是刚才我们提到什么呢?就是你 mn 是这样子的,你可不可以反过来,你看我写了个若 m 是这样子的,也有可能性是这个是 能和 m 这样反一下,反一下之后你看这个就变了呀,对不对?你 m 的话做一个这个水平的线给他去相交,你看啊,我们这个呃 h 点的位置什么就变了啊,你又会有另另外一条直线那么两条直线的交点是不是一定就是一个重点啊。我们这个定点呢, 这样就比较靠谱,比我们猜到靠谱对吧。那么这个的话大家自行去算一算啊。我就直接写了啊就来到这条直线的话是这样一个情况就正常直线胶带是这样看哎,很明显是零豆花嘛,对吧。所以我们这个两直线的焦点即为这个定点啊,也是零豆花哎这样就找到了呀,明白吧。找到一个定 点之后就为我们指明了方向啊,你看本来在黑暗中探索的现在已经看到了黎明看到了这个导向但是真正的恐怖才刚刚开始。好吧,来我们来正式较量一下这道题哈,我们假设他有斜立的时候就是这样一个图了哈那么我们这样的话呢这个直线射出来啊,点斜视啊然后的话呢接下来就正常连立啊, 呃两天我们写点歪哈就得到这样一个式子啊,这是个常规的运算啊,然后自然而然写这个伟大定理两分之和两分之几呗,对吧。呃写完之后干嘛呢写完之后不知道干嘛了哈。到这就那就先停啊,你看你要干嘛。我们这道题啊我们其实为了是写那个一绳子直线方程对吧。 所以的话呢我们是需要知道说 m 的坐标哈,比如说他是 x 一 y 一哈,然后这个 n 的坐标是 x 二 v 二啊,然后这样的话你通过 m 的坐标啊我们就可以知道这个梯点的坐标吗他的这个纵坐标的话跟他是一样的是 vr 一对吧?那我们他的横坐标的话,带进那个 ab 这个方程啊,会得到是二分之三倍的外一,再加上一个 二啊,这样的话呢,你把这个梯点的坐标成个两倍啊,就终点乘个两倍,减掉 m 的坐标,可以得到这个 h 的坐标啊。呃, h 的坐标的话是三万一,再加上一个这个六啊, 再减 x 一,然后再他的动作标是 y 一啊,之后我们去写这个 h n 的方程哈,这个你看非常的麻烦啊,你斜立的话,比如他俩是动作非常减肥,红色非常减啊,比较麻烦,但是也没有办法然后点些事啊, 因为这两个坐标你看都是一个什么呃,以 s e, x r 和 yuy 啊来呈现出来的,所以大家看到说这就是我们的这个直线 hn 的一个方程啊,简直是非常恶心啊 啊,化解也没法化解,你看这怎么弄对吧?啊,那么你不要忘了我们要证明他什么哎,证明他过一个定点,而且这个定点是谁是零豆花呀,所以怎么样?哎,我们的话你不是说哎一种化这个把他化解哎,然后再正出来他过这个点,另外的话验证哎,带进去如果他成立的话是不是 就可以啊?这道题我们要用代理性这种方法啊,所以我们将这个零分带入啊,带入的化解了,看是不是成立了,对吧?那你把这个分部乘过来哈,然后这边右边撑开,我们进行整理啊,整理的结果是 这样一个式子啊,非常非常复杂啊,其中这个地方两根之和哎,这里的话你看还要有 vi 一加 v 二啊,我们可以转换成 s e x, 然后的话呢?呃,这里是 y 一乘 v 二啊,然后这个地方还有这个东西啊,呃,我们把这些东西都要换掉,换成 k 啊,你看他肯定会等于零就行了啊,被剩下一句印算啊,我们把这些东西就挨个处理处理好吧,这个已经处理过了,处理他和他还有他啊。 呃。我们其中把这个 y 一加 y 二啊换成这个哈,然后 y 一乘 y 二,你看都换掉哈,都换成 x s 二,这样一乘开是肯定是可以转的对吧啊?然后化解就可以得到说关于 k 的一个事实,或者说都换了,刚才我们不是削了 y 吗?你你也可以再削一次 x 也一样啊,计算量基本上差不多啊,这是我们化 之后的一个这个结果哈,这解决了他俩哈,那么接下来的话我们还要解决谁呢?哎还有一个是这个东西是吧?解决他的话我们需要去把这个 y 二 y 一啊都换成 x 二二,然后 x 一啊,就利用这个直线方程了, 然后把这个展开就可以了,展开的话你合并一下啊,然后就可以得到这样一个式子,然后再把这个两根之几,两根之和带进去啊,就得到全是 k 的一个式子啊,那么接下来的话只需要把刚才的你看这个带入,这个带入,这几个都带入啊,进去的话点它是不是零,这就可以了。好吧, 呃,那我们把这些东西代入的这个过程哈,就大家自行代入化解一下就可以了。剩下的就是纯粹的话呢,是非常鲁莽的一些计算啊,就没什么技术含量了,但是你要写啊,因为这个很容易涉嫌伪证,好吧,所以我们带进去之后发现这个东西是什么?是一个成立的哈。成立是啥意思呢? 成语说明的话,这个 hn 的话呢?是哎,经过这个点谁啊?已经都发了,就是我们经过验证之后啊,所以我们大家去想一想。综上的话,你看我们 每种情况的话,这个直线是不是都会经过这个零豆花啊?这就整道题啊。啊?这个想法的话呢,还算是比较简单的,但是计算量的话呢,是巨大无比,有点变态啊。所以平时的话呢,你要练就这种变态的计算能力啊,才能稳妥拿下啊。
1878孟见数学 13:10查看AI文稿AI文稿
13:10查看AI文稿AI文稿大家都说二零二二全国一卷十二题难出天际,那么方老师就用全网最简单的方法给你讲清楚,保证你能听懂,而且觉得这道题并没有你想象那么难。来,咱们开始啊, 他说,已知函数 fx 和 gs 定律都是 r, 且 fx 加 j 二减 x 等于五, jx 减 f, x 减四等于七,若 y 等于 jx, 图像关于 x 等于二对称,而且 j 二是等于四的,则这一串等于多少? 好,这道题你拿到手大概率是一头雾水,他考的是这个抽象函数的对称性、周期性啊这些,但是呢,哎,就看你怎么找思路。来,我告诉你啊,这道题你看,这么做啊,是比较简单的,怎么做呢?看 啊,他这里面又有 fsx, 又有 jx 在同一个式字,咱们这道题求的是 fxr, 如果你直接去求 fx 的关系,能找出来,但是特别麻烦,而且很多人已经死在这里了。那么啊,你看啊,方老师是怎么做的? 那么这道题告诉你看,这里有个条件, jx 是关于 x 等于二对上的,而且 j 二等于四,有什么意思? jx 给的条件比较多,是不是?那么所以咱们能不能把 fx 消掉,找 jx 的关系呢?来,咱们演示一下啊,你看, 呃,这边是 fx 这么多,这边是 fx 减四,好,咱们化解一个啊,咱们比如说,嗯,把 x 减四带入第一个是, 好吧?啊,然后把 x 减四带入第一个式子啊,就是让 x 都等于 fx 减四,能明白吧?哎,你看是不是变成这样子的, 加上 j, 这个就是二减去 x 减四等于五,好,能看清楚啊。来,接下来我把这个式子化解一下,嗯,前面不动,后面站岗啊,二减去 x 减四,是不是应该变成的事儿? 六减 x 没问题吧?好,那么接下来我把第二个十字超过来啊,你看一下, jx 减去 f, x 减四等于七, 好,那么这两个式子你看一下,有没有发现我这张两式相加,是不是就把这个 fx 给削掉了?好,两式相加啊,是不是就变成了是 x 加上这六减 x 等于十二,是吧? 好,问题来了啊,很多同学看到这步就死了,好,哈哈哈,来,在这啊,这个在方老师系统科学讲过,这叫中心对称, 咱们已经很自从二零一六年考过中心对称。这么难的啊,再也没考这么难,其实今年考的确实有点难啊,那么这是咱们就是放的是系统课里的一个结论啊,是怎么说的呢?是这样子的啊,就说我给你写到最上面吧, f x 加 a 加上 f, 负 x 加 b 等于 c, 那么如果 fx 满足这个式子,那么它是关于二分之 a 加 b, 逗号二分之 c 对称的啊,明白,那么也就是说 他这个反应的是中心对称图形啊,好,能看清楚吧。那你知道这个节目来套一套他关于谁的事啊?那么看出来,你看啊,这里面相当于是 x 加零,这是六减 x 吗?是吧,哎,他关于谁的事?关于的事儿, 二分之零加六,是吧?哎,逗号二分之十二,那么也就是关于的是三逗号六对称,哎,你看到这啊,你看这又是咱们系统的已经啊, 他这个 g x 关于 x 等于二对称,又关于三的话,六对称,是吧,哎,我写到这, 哎,你看,一个对称轴,一个对称中心,哎,这又是个结论啊,一个对称轴,一个对称中心,那么他的周期是多少呢?是四倍的啊, b 减 a。 好,这个东西怎么去理解呢?哎,如果你不清楚,你看放 画一个适应图像,你看啊,一告诉一个对称轴,告诉一个对称中心,你没有发现一个对称轴和一个对称中间正好是四分之一个周期,也就反过来他完整周期是不是四倍必减,是吧,那么你看啊,他是关于 x 等于二,在这个横坐标是三,是吧?哎,所以它的周期是多少?四倍的三减二就是周期是四,明白吗?好,那么啊, 你看咱们这个 jx, 你看条件已经知道很多了,是不是啊?那么咱们是不是可以求出 jx 的其他的值,对不对啊?那么这时候求 jx 其他值怎么办呢? 哎,这个手啊,一种方法就拿这个式子去人工推倒,另外方法是画图方的时候告诉你画图最简单。好,来,咱们一起画一下啊,来,咱们画这 x 啊,我这画一下大概, 嗯,好,你看啊,这个字他应该有第一个,这二是等于四的啊,这二大概是等于四的哈,这是四, 我这图画小了,哈哈哈,不急,好,咱们挪一挪。嗯,好,大概再画的大一点点啊,画到这吧,二 不行啊,不行,这个地地方不够啊,不够,算了,还是得大概花在这啊。啊, 这个,这个地方是二啊,啊,这个地方是一,然后三四五六。好,这个啊,二的时候是四啊,大概是这里。好,那么接下来一下啊,咱们猜是个 x 等于二对称吗?把对称轴画的啊, x 等于二, 然后他这个关于三豆花六对象,那说明什么?是不是 jx 是过三六点的对不对啊?所以这三的时候是等于六啊,这是四,这是六啊,哎,大概是这样 好,而且这个函数是关于三六点对称的,是不是?哎,我问你,你说 x 等于四的时候,他等于几? 是不是就等于八嘛,对不对?哎,是不是上下都这么对上?你看啊,咱们画到这还有等于四的时候等于八,对吧?哎,我把它连起来, 哎,这个是不是是八吗?能理解吧。好说,你看,这是装修队上用到了啊。接下来刚才说他是关于 x 等于二队上的,对不对?哎,所以左边头像怎么画,是不是?哎,就证明这个微型是吧。 x 等于一 一的时候,这 x 是等于六的,二, x 等于零的时候,这是等于八的,没问题吧?而且,哎,你有没有发现,这么画出来以后没有发现零到四图像全部有了,他周期又是四,哎,是不是后面图像就一模一样,哎,往左画往右画,他图像都是这样子的, 满意吧?哎,你有没有发现,你我图像一画, gx 的各个值就全部都知道了,是不是?好,我 gx 全部都知道,我回过头再求 fx 行不行,特别简单是吧?哎,咱们比如说咱们就拿第一个式子来看啊,好,我用黑色的写二, 你看 f x, 嗯,这是这个啊,加上 j 二减 x, 等于我把这个 j 二减 x 弄到右边,好吧,等于是五减去 j 二减 x, 是吧? 那你看啊,到这到这啊,你能不能看见?因为 jx 是个周期四的函数,那么 fx 一定也是周期为四的函数,能看明白吧?啊,这个式子如果你看不明白的话,我给你稍微改一下啊,你看啊,咱们这个 jx 的是关于 x 等于二对称,是不是?关于 就是这个 x 等于二对称,所以咱们这这个 j 二减 x 是不是就等于 j 二加 x 呀?是吧,这是一个结论啊,这个会啊,这个要不会?哈哈,来,我在这给你科普一下啊,我用一个绿色写啊,我写下如果 f a 加 x 等于 f b 减 x, 这种情况是关于 x 等于二分之 a 加 b 对称的。好,那么 这也是结论啊,咱们这个题整体全部都考的是中。呃,这个抽象函数的对称性,周期性啊,必须会,这个结论 我觉得任何一个老师都会讲的啊,就咱们这个中心对称其实考了很多年没考了,大家掌握不了,但是这个轴对称是一定要会的啊。好,那随你看, f j 二减 s 就等于 j 二加 s, 你看这个是关于二分之二加二,是不是二零 就是 x 等于二对上吗?是吧?好,那么啊,我把这个 j 二减 x 换成 j 二加 x 好不好?你看啊,这样换完以后是不是等于是五减去这 x 加二,是吧?哎,我这样写实际是为了你好理解啊,如果方法是自己算法啊,拿第一个式子算啊,你看这个式子写出来了,这题是不是搞定了?哎,你看 刚才是 fx 和 jx 是有明确的关系的, jx 是周期是四,这个很明显, fx 也是周期是四吗?那所以咱们只要把这个 f 一、 f 二、 f 三和 f 四是不是都算出来就可以了,对不对?那请问 f 一是多少?你看是不是五减去这三是吧? 嗯,这三,这是六嘛,对不对啊?所以五减三,五减六的话是负一啊,这样 f 二是多少?是不是就是五减瘸这四, 这四是八吗?哎,咱们把这也画下,五的话这又是六,六的话这又是四啊,好,所以五减,呃,这四就是五减八是负三,然后 f 三是 是 f 三是等于五减去这五等于的是五减六,负一是吧? f 四等于的,是 啊,五减去这六啊,这六十四,所以等于一,是吧,哎,就可以了吗?那这个有了,你看后面这就好办了,是吧,他这道题其实考的还紧了吗?他如果这求的是从 配等一到二零二二啊,求这个 f 这么多的值,是吧,那这个,而且大家毫不怀疑他一定是周一函数是吧,哈哈哈, ok 啊,好,那么来,接下来咱们把这个算一下啊。嗯,因为你看这个啊, k 等于一加到二十二,这个 f k 啊,那么这个二十二除以四明显是五个周期,是吧?哎,所以 就看五个周期啊。来,咱们一个周期加起来多少?负一加负三再加负一再加一,是不是就是负四嘛,是吧,哎,所以等于多少这个东西就等于, 嗯,这是负四乘以五于二嘛,是吧?于二的话剩下的时候就是 f 一加上 f 二嘛,没问题吧?哎, f 一是负一, f 二是负三,是吧?负二十 减一再减三是多少?负二十四,哎,答案选 d 搞定,听明白了吧? 好,你可以去呃,在网上跟其他老师对比啊,方老师觉得这个方法是,呃,最简单的。好,全网最简单的,哈哈哈,好,你听见没有了吗?来,在这啊,来,方老师再给你理 下啊。这道题还是很难的啊,首先这道题他给的是 fx 和 jx 的关系,嗯,这道题其实大家第一反应肯定是把 jx 也给消掉,然后去找这个 fx 的关系,那么 我告诉你是可以找到的,你能正处 fx 是只周期函数,也是中心对称,也是轴对象都能正出来,但是特别麻烦。方老师线下都试过了啊, 反过来,因为他这个 gx 图像啊,他给了两个条件是吧?两个条件不少了啊,哈哈,这个是抽象函数啊,那么既然,嗯,这个 jx 相对来说比较好算,所以咱们把 fx 消掉。哎,前面的话就把 fx 消掉就可以了啊,你怎么消都行啊,只要是把 fx 带纸把它消掉就可以了。消掉了然后就找之后他关于三等会零队长,所以这个时候好的,接通通,都是中心对 对称,轴对称周期性的知识是不是?哎,通过这个对称性,嗯,中心对称啊,轴对称把周期找到了,而且各个值都求着 求这种周期性的图啊。有周期性对称性求职的话画图最简单,然后求你要是比如说不想用这个,然后你就是那个自己去推导也行,特别麻烦啊。你自己可以尝试一下这个值求出来 fx 几个值是不是都求出来,这道题就搞定了,明白吗? 嗯,整体来说这道题还是比较难的啊,但是,嗯,再难他也有方法嘛,是吧,好,你学会了吧。好,那你还不关注一下,哈哈哈哈,拜拜。
219方程老师讲数学套路 00:15查看AI文稿AI文稿
00:15查看AI文稿AI文稿挺难的哈哈哈哈哈哈我们俩考不怎么样应该比平时最后做的难忘难难难多了。估计一到二十五年还是没啥问题。就就那样吧。哈哈哈你是学霸级的是吧?就那样吧。哈哈好好加油加油。
7.7万都市报道 02:24查看AI文稿AI文稿
02:24查看AI文稿AI文稿教育部回应了今年高考数学为什么这么难?今年高考数学一考完,很多孩子是哭着走出考场的,看着真让人很心疼。疫情三年,很多孩子网课就上了三年,那为什么数学还这么难呢?根据教育部考试院的回应 和对这次考试试卷的总体分析,我总结了三个考察重点,对孩子备战接下来的各类考试都有用。 第一个是考察基础知识的灵魂运用。如果你仔细看过试卷就会发现,乍一看这些题根本动不了笔,但仔细一看,考的全是基础知识的变形。比如全国一卷第五道选择题, 考生一看互字,这是啥?没概念了?那这其实就是小学五年级学的字数。教育部考试院回应说,这 是重在强化技术考察服务双检政策的实施,助力基础教育的体制增效。孩子如果没有吃透技术知识,也许能勉强应付小学、初中考试,但真正到了高考,肯定会原形毕露。 那怎样才能吃透基础知识呢?就是一定要做好科学的预习和复习。那么第二呢,是考察数学思维的生活运用。 总有人说,数学学那么好有啥用,以后长大了又不搞科研,又不当科学家,这是很多人对数学最大的误会。数学最大的用处是什么?那就是在生活当中运用全国假卷第二题就以垃圾分类为背景,就是考察学生数据分析的能力。 第三点是考察学科的联系。教育部回应说,这次数学考试啊,尤其强调知识点之间的 再联系,引导学生形成知识系统。全国甲券理科第八题就取谈于梦溪笔坛新高考第二卷第三题 就取材于中国古建筑中的举驾结构。还有一道题呢,直接用酒量算数、文案文来出题,那这不仅和高度历史有关了,也和语文能力息息相关呀。总结一下,回归基础、联系生活、跨学会运用, 这是学好数学的三大根本方向。数学是所有科目中最能拉开差距的学科,虽然这次数学难过了不少同学,但等分数出来呀,相信依然少不了满分的。好了,今天就分享到这里,我是李老师,关注我,每天分享学金干货。
1118高考逆袭李老师 15:57查看AI文稿AI文稿
15:57查看AI文稿AI文稿好,我们来看一下二零二二全国已卷的这个选择压轴题,它考察的是函数的综合性质啊。首先呢,我们先读一下这个题目,已知函数 f x g f 的定义都是 r, 然后呢给出我们两个式子, 若 g x 的图像关于 x 等于二是对称的,并且呢 g 二十四,让我们求他的前二十二项的和, 然后接下来我们会通过两种方法来写一下这个题目,其实第一种方法的话,我们可以把它当成类似是一个数列求和的问题,然后我们啊根据这个地推关系呢进行求解 啊,所以这个第一个方法,人家让求的是 f k 它的 前二十二项的和,那所以我们其实是想得出一个式子,这个式子里面只有 fx 对不对?那所以第一个式子和第二个式子它是可以进行连例的, 连例之后我们希望把这个 j x 给它削去,对不对?所以我们可以怎么去削呢?然后这个 j x 又关于 x 等于二对称, 没有可以得出什么样的一个式子呢啊?它关于这个线对称,其实我们可以得出这个 g x 等于 g, 然后四 g x, 或者是我们得出 g x 加二等于 g 二减 x, 对不对?到底选哪一个?我们就看这个式子里面等式里面然后出现的是二减 x, 对吧?所以第一个式子我们可以给 整成 fx, 加上一个 gx 加二,然后等于五,嗯,第二个式子的话,我们希望是把这个嗯把这个 g 给消去的,对不对?所以我们希望出现 x 加二,那也就是把第二个地推式里面 所有的这个 x 全部换成 x 加二,那后面就变成了 x 加二减四,也就是 x 减二等于七,然后这两个式子相减,嗯,所以减完之后我们会得出一个 关系啊,也就是 f x 加上一个 f, x 减二等于负二,那所以这个不就是一个嗯,隔向求和的问题吗?对不对? x 和 x 减二中间其实是隔了 一项了啊,然后我们要求的是前二十二项的和。那大家思考一下,我们这个时候是不是需要分机油讨论?所以第一种的话就是当 x 为啊。基数的话, 那我们可以算出什么呢?我们可以算出从倒倒着算啊,所以倒数第一个它是 f 二十一, 那后面这个是 f 十九,对不对?所以我们一直算到 f 三还是 f 一呢?我们算的是 f 三,为什么呀?因为二十二个数里面, 他有十一个是基数,然后有十一个是偶数,但是这个基数的话啊,必须是相邻两项相加,它是一个定值,那么我们必须要成对出现,对不对? 所以我们需要取掉一个,我们取的是第一个,也就是 f 一,然后啊,剩下十个恰好是凑成了五对,那么它的和应该是负二乘五,所以是负十,对不对?然后第二种情况,也就是当 x 为偶数的时候 啊,我我们会得出 f 二十二,然后加上 f 二十,然后一直加到 f 四还是 f 二呢? 是 f 四,这个原理和刚才一样啊,因为十一个偶数,我们又要凑成整对,所以需要取掉第一个,也也就是 f 二,所以剩余仍然是五对, 那么它的和是不是也是一个负十呀?嗯,然后它俩相加之后,其实我们会得出的是 f 三加 f 四一直到 f 二十二,所以我们其实是少了这个 f 一和 f 二,对不对?所以接下来我们需要推 f 一 和这个 f 二的值,然后要推这个值的话,人家给出的是 g 二,那么我们希望把这个 f x 和 g x 是不联系到一块,所以怎么去联系呢?那这个第一个式子我们是不可以直接啊变成, 嗯 f x, 直接就变成五减 g x 加二,对不对?所以要算这个 f 一的话,那它就等于五减去一个 g 三, 然后要算 f 二的话,那就是五减去一个 g 四,所以接下来我们的任务就是算出 g 三 和 g 四,是不是就可以?所以我们需要推出这个 gx, 它的一个性质,或者说 gx 它本身啊具有的一个式子。那此时我们需要干什么?我们是不是需要把这个 f x 给它消掉,然后得出一个 g x 的一个关系,对不对啊?所以接下来我们就需要啊,像刚才一样消这个 f x, 那削这个 f x, 我们就希望两个式子里面出现独立的 f x 其实就可以了,然后那这个这个式子有独立的 f x 呀,所以他要保留,对不对? 后面这个我们再负一个值,让 x 全部变成 x 加四,那么这个式子就变成了 g x 加四,减去 f x, 然后等于一个七, 这两个式子最后相加,是不就得出啊?一个关系吧?但这个式子 其实不太好啊,我们拿上面这个式子进行合并啊,比如说他是一,然后这个是二,这两个式子怎么样呢?这两个式子我们相加,然后会得出一个关于 gx 的一个等式,这个等式是 g x 加四,加上一个 g 二减 x, 然后等于十二。其实根据这个式子我们可以推出 g x, 它其实是一个中心对称的一个函数,我们可以推出对称中心是三六,对不对啊?这个是 啊,一个啊,这个是一个。然后我们要,呃,求这个 g 三的话,我们应该看的是哪一个?是 我们应该看的是这两个对不对啊?也就是和 g x 有关的啊?所以我们写到右边吧,这个 g x 加二等于 g 二减 x, 然后 gx 加四,就啊加上一个 g 二减 x 等于十二。那下面的求值的过程实际上就是负特殊值的过程,我们要求这个 g 三的话,所以大家可以负值,那这个这个是怎么负?负一,让 x 等于负一, 第一项是 g 三,然后第二项是不是也是 g 三?所以我们推出 g 三是六,那么它是五减六,也就是负一吧,啊,就轻松的求出来了。然后那我们需要求 g 四的话,那怎么负?让 x 等于零,所以这个 g 四 加上 g 二等于十二,这个 g 二的话是四,那么推出这个 g 四应该是八,也就是五减八,所以是负三,所以 那这个和我们不就很轻松的就求出来了吗?所以这个和的话啊,嗯,这个圆是应该等于负十, 加上负十减一减三,所以我们求出来应该是负的二十四,这个是法一,我们用基偶求和这个思想进行计算啊,所以接下来我们用法二来解决一下这个问题, 这个法二的话,纯粹是没有看出这个基友求和的这个关系啊。然后,呃,那接下来我们肯定是希望得出一个式子,一个式子里面 只有 fx, 一个式子里面只有 gx, 对不对?所以就从这两项入手。如果我们想推的是 fx 的一个关系,也就是我们需要销 gx, 要销 gx, 那这个二式是不变的 啊,要销髓就让髓是 g x 啊,就是这个电量是 x, 那么我们希望,嗯,第一个式子里面出现什么 啊?出现这个 g x, g x, 对不对?所以我们可以负值,嗯,那这个 x 我们负多少呢?让 x 等于多少? 二减 x 吧。所以啊,这个式子就是 f 二减 x, 然后加上一个 g 二减二加 x, 也就是 g x, 然后等于五。第二个式子我们照抄, 所以这两个式子我们相减,就得出一个 f x 的一个关系。 嗯,所以其实我们可以推出这个 f x, 它是具有中心对称性的,对不对?它是关于 啊,负一负一是中心对称的,有没有用?我们先放到这,那第二个,既然我们推出了 f x 的一个等式,那同理我们是不是需要推这个 g x 呀?要推 g x, 那么需要出现独立的 f x, 第一个保持不变。 第二个我们希望出现呃,独立的 f x, 所以我们可以负 x 加四,对不对?所以就是 g x 加四,然后加上一个 f x 加四减四,也就是 f x 等于七,然后这两个式子们相减,就会得出啊,就会得出什么 g x 加四, 然后减去一个 g 二减 x 等于二,所以我们推出这个 g x, 实际上它,呃,这个是相减的啊, 我说呢,这个,这个后面这个中间应该是减号吧,这是减号,所以啊,我们让上减下吧,所以上减下之后,这个是 g 二减 x, 然后, 呃,相加啊,相加,然后加上一个 g x 加四等于十二。所以我们推出 g x 是一个啊,也是一个 中心对称的一个函数,它的对称中心应该是三六啊,关于三六是中心对称的,并且它是关于 x 等于二轴对称啊,关于 x 二等于轴对称。这个时候我们可以利用什么呀?我们可以特殊化,就把它当成一个, 嗯,当然这个不是 x 轴啊,不是 x 轴,呃,当成一个三角函数,然后一个是对称轴, 这个是 x 等于二,然后一个是对称中心是三六,那么我们就可以认为这个周期应该是四 啊,因为这一段长度是一,这个恰好是周期的四分之一嘛,所以周期是四啊,周期是四,嗯,所以啊,要求这个 f k, 目前我们知道的是 g 二啊,是 g 的一个式子,所以啊,我们可以就是把这个 f x 用 g x 来表示,对不对?所以 f x 就等于五减去 g 二减 x, 然后要求他的前二十二项的和,所以我们需要啊,实际上就是求这个式子前二十二项的和,对不对。我们推出这个 g x, 它具有 这个周期性,所以那我们推出一个周期,他的数值分别是多少?嗯,这个 g 二是四,那根据这个 g 二,我们可以推出什么?我们可以推出 g 四吧, 就是看上面这个柿子,嗯,换一下颜色啊, 啊,就是看上面这个式子,我们开始复持,让 x 取零,那么我们推出这个 g 四,应该是八 啊,记四十八,然后推出记四之后,我们希望推多少啊?希望这个记三也想知道呀, 然后记一我们也想知道,对不对?所以要推记三的话,是不是仍然是负值负负一,所以我们推出这个记三,应该是六啊,应该是六,然后记三知道了,那么这个记一呢?要推这个记一,我们可以让 x 取多少?大家思考一下 啊?这个关于 x 等于二对称,我们啊把这个式子也写出来, g 二减 x 等于 g, x 加二,所以我们要推 g 三,我们可以 啊,让上面这个式子负一个一,对不对?然后推出记一就等于记三,那么这个记一就是六啊,就是六,嗯,那这个一二三四,其实恰好可以认为他就是一个周期,对不对 啊?他就是一个周期。嗯,然后,呃,要求他的前二十二项的和,我们看一下他是什么啊?所以这个求和,也就是圆式 应该等于五乘二十二,对不对?一共是二十二个五,后面的话是什么呢?后面是,嗯, g 当 s 等于一的时候,它是 g 一,然后加上一个 g 零,再加上一个 g 负一啊,加上 g 负二,这个是一个周期, 等等,一直加到这个最后啊,加最后。所以那我们先算出这个记一, 记零,记负一,记负二,他这个数值以此类推啊。因为,嗯,从任何一个数作为起点,然后我们取连续取四个,他都是一个周期的,所以从一开始的话,大家思考一下啊。他是 啊,从这个四三二一,他是八六四六,然后后面肯定也是八六四六,然后这个是对应的是 g 四,然后 g 三, g 二, g 一,这个是 g 零, g 负一, g 负二,对不对?然后我们是从这个 g 一开 开始,也就是六八六四,这个是一个周期,然后他每一个周期他的和都是一个定值,是二十四,对不对?嗯,然后有几个二十四呀?也就是看有几个周期,所以我们拿二十二除以四 五个周期于两个,所以最后的和我们可以轻松的求出来啊,写上面了啊,写上面那就是五乘二十二 减去啊,一共是五个周期,每一个周期都是二十四,后面的话多两个,多拿两个 六和八,对不对?也就是加个十四,所以最后我们求出来仍然是负的二十四啊,这个是两种方法啊,两种方法。 嗯,很显然这个法医可能计算量会更小一些,大家可以选择适合自己的方法来解决这个问题。嗯,如果大家有更好的方法,欢迎评论留言,我们下个视频再见。
60欢姐带你学数学 00:58查看AI文稿AI文稿
00:58查看AI文稿AI文稿北大女生做高考数学压轴题要多久? 计时开始 用了两分五十三秒,看下结果吧。再做一下另一套卷, 计时开始 用了两分五十九秒,看下结果吧。今年全国甲乙券还蛮简单的。
103.5万奶黄包🌙 00:15
00:15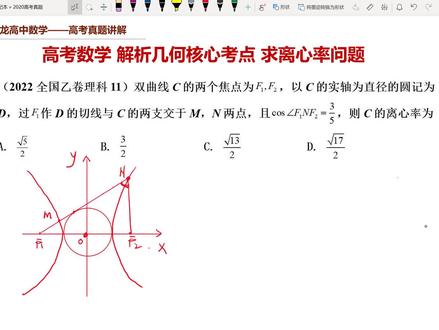 04:09查看AI文稿AI文稿
04:09查看AI文稿AI文稿二零二二年全国已卷理科第十一题双曲线 c 的两个焦点为 f 一 f 二,以 c 的实轴为直径的圆,即为 d。 过 f 一做 d 的切线,与双曲线两只交于 m 两点,且口在角。 f 一 n f 二等于五分之三,求双曲线的离心率。 那么这里边咱们要求离心率,实际上就是建立 abc 之间的一个关系,是不是啊?那这里边呢?我们根据所给条件,首先画出图形, 这是以这个圆呢,是以十周为直径的圆,那就说明这个圆的半径就是 a。 过 f 一做这个圆的切线,交两只于 mn 两点,那这里边咱们是 实际上需要判断一下 mn 谁在左边,谁在右边,怎么去判断呢?我们根据后边的一个口塞值,他是正,就说明这个角是锐角, 那角是锐角,显然这个 n 点应该在右侧,才能保证这个角是锐角。如果点 n 在左侧的话,那么这个时候 fenf 二十个钝角,他的预选值就应该是负的,是不是?所以我们确定 m 在左边, n 在右边, 那这个时候呢,接下来咱们看这里边有相切条件,我们设切点,假设为 p, 那么连接 op, 这是垂直的 op, 这个边就是 a, 然后 feo 是 c, 那显然根据个股定理,这个 p f 一,这个边长就是 b, 那么我们再过 f 二,做这个期限的垂线,适合垂出时 q, 由于 o 是 f e f 二的终点,那么这里边显然 o p 是这个中卫线,是吧? o p 是这个三分的中卫线,那么这个 q f 二就应该是二 a, 然后这个 p q 呢,就等于什么 p f 一,所以这个 p q 的边长是 b。 好, 那接着我们再看这个三角形 nqf 二,正好现在也是直角三角形,我们根据这个口算值等于五分之三,我们不妨设这个鞋边是五 x, 那么这个 nq 就是三 x, 是吧? nq 是三 x, 那么这个 q f 二是不是就 是四 x, 对吧?好,那因为这个 q f 二是不是现在应该等于谁?等于二 a? 二 a 等于四 x, 所以我们就得到 x, 是不是就应该等于二分之一 a, 那么 x 等于二分之一 a。 知道之后,那么 q n 是不就是三 x 就是二分之三 a, 然后 nf 二, nf 二呢?就是五个 x 就是二分之五 a。 接下来我们根据双曲线的定义,因为 n 点在双曲线上,根据双线定义, nf 一减去 nf 二,是不应该等于二 a 啊? nf 一是谁啊? nf 一,他是个 b, 加 b 再加上 qnqn 是二分之四 qn 是二分之三 a, 那就是二 b 加上二分之三 a, 减去 nf 二, nf 二是二分之五 a, 他应该等于二 a, 那这里边呢?我们看整理一下,二 b 就等于这是三 a, 也就得到 a 分之 b 等于谁啊?二分之三,那么我们知道双曲线的离心率,他应该等于根号下一加上 a 方分之 b 方, 是不是就等于刚好下一加上四分之九,也就是刚好下四分之十三?记二分之刚好十三。正确答案选择 c。
125延龙高中数学 04:49查看AI文稿AI文稿
04:49查看AI文稿AI文稿各位同学大家好,从本期视频开始,我们将开启新一轮的高考每日一题。这是第一题二零一二年高考全国已卷离开的第四题。 好,我们直接呢从这个地方开始看,稍微研究嫦娥二号绕着周期与地球绕着周期的笔直用到数列边边是什么样的玩意呢? b 说等于一加 a 一分之一, b 二呢?是一加 a 一加 a 二分之一分之一, b 三呢?是这么一个结构,一个年分数的形式吧。好,以此类推。说 an 呢,说这个 a k 啊,属于正整数, k 呢,属于 k 呢,是等于一二一直往下对吧?然后让我们选出正确的选项。好,我们看一下选项 a 选项比较的是 b 和 b 五的关系。 b 呢,是 b 三和 b 八, c b 六, b 二, d, b 四 b 七。这个题啊,如果在考场上,你一时想不出好的方法, 一是想不出好的办法的话,你倒是可以复职。你就假设这个 a 一, a 二, a 三对吧,一直往下都等于一。然后你来算一算也是可以的。好,我们来看一下这个题里面有什么样的秘密啊。 先看 a 选项 a 选项比较的是 b 一和 b 五的大小关系。注意 b 等于多少啊。 b 是一加 a 分之一吧, b 五呢,一加上好 b 五的话,你如果写的话,这个狮子啊,很长,它实际上呢,根据这个规律,肯定是 a 一。这个后面呢,有一堆东西。 这一堆东西呢,我暂且用 x 来表示,反正 x 大, x 啊,是大于零的,我不管是多少的,他既然大于零,那你看这个 a 一 比这个 a 加 x 是不来的小。那么倒过来过后呢,是不是就来的大了。所以 b 啊,应该是大于 b 五的。 a 错。好,第二个选项, b 选项,我们比较是 b 三和 b 八。 ok, 我们把 b 三写下。 b 三呢,就是他把它抄下来啊。好, b 八。同样的道理,你要写的话很长,我不用完全写下去, 我只只用在 b 三的基本上。这原来这个地方不就到 a 三停掉了吗? a 三分之一,现在呢,相当于 a 三加大外分之一,这个大外呢,也是个正数,对不对?这样的话,你注意啊,这一个 a 三分之一比这个 a 三加大外分之一是来的大的。倒一次,因为这个地方有一个分之一吗?是不是变小了?再倒一次,是不是又变大了?因此 b 是不就错了?应该是 b 三大于 b 八吧, 对吧?好。 c 选项是 b 六和 b 二。 b 二多少啊? b 二就是一加上 a 一加 a 二分之一分之一。 同样的道理啊,这个思路都一样,后面我不用管。反正呢,这个 b 六,就是在他的基础上, 这个 a 二后面加了个大 m, 大 m 呢,也是大一点的。这样的话,你看这一部分比他来的大。倒一次,是不是变小了,所以比二小一比六。其实做到这个地方呢,你大概找到规律了什么样一个逻辑了吧。好,那你看 b 四和 b 七, b 四的话,把它写一下,是不是这个样子。 b 七呢,就是在这个 a 四的后面再加个大 n 吧,大 n 呢,也是大于零的。好,你看 这个 a 四分之一比这个 a 四加大一分之一来的大。倒一次,这个地方倒一次,变小,再倒一次,变大,再倒一次,是不是变小。所以 b 四呢,是小一比七的。因此啊,这个 d 选是正确的吧。所以呢,你答案选 d 对吧? 哦,坐在这个地方呢,你可以总结下这个规律。你看,哎,他比较的是什么? b 和 b。 五,你注意他倒了几次,他只倒了一次呢,对吧?这个地方呢,倒了几次是不倒了三次对吧? 这个地方呢,倒了两次对吧?分之一分之一吧。这个地方倒了四次,是不是倒了四次啊?倒了一次的时候是比一呢,大一比五呢。这个倒了三次的时候呢,比三是大一比八呢 啊,倒了这个两次和四次的时候呢,都是变小了。比二小一比六,比四,小一比七,是不是这么一个概念。好吧,那这个题呢,其实呢,并不需要你怎么算的,你只要 用一个微质量把后面那一坨东西把它剃光掉就 ok 了。好,谢谢大家。
371高中数学施老师








