理想气体状态方程高考题
粉丝93.5万获赞913.0万
相关视频
 08:08
08:08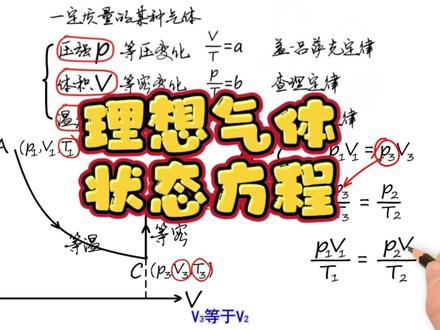 03:30查看AI文稿AI文稿
03:30查看AI文稿AI文稿描述一定质量的某种气体的状态参量有三个,压强、体积和温度。 前面我们所提到的每个实验定律都是当一个餐量不变时,另外两个餐量的关系。现在我们研究三个状态餐量都可能变化的情况下,他们之间遵从的数学关系。 我们借助于压强于体积图像,若一定质量的某种气体从 a 状态 p v 一 t 一,变为 b 状态 p 二 v 二 t 二。我们取一个合适的中间状态 c, 使 a 到 c 经历一个等温变化,再经历一个等容变化,从 c 到 b, 若 c 状态的状态参量为 p 三 v 三 t 三,那么从 a 到 c, 由波伊尔定律可得 p 一 v 一等于 p 三 v 三。从 c 到 b, 由查理定律可得 p 三比 t 三等于 p 二 比 t 二。将两室多有地向 p 三带入,得到 p 一为一比 t 三等于 p 二, v 三比 t 二。因为 a 到 c 是等温变化, t 三等于 t 一。而从 c 到 b 是等容变化, v 三等于 v 二。 因此, p 一 v 一比 t 一等于 p 二, v 二比 t 二。这说明一定质量的气体在每一状态时,其压强与体积的成级与热力学温度的比值是相等的, 且慢。你肯定会问,这部分气体若变化为其他任意状态,例如 d 状态和 e 状态也会如此吗? 事实上,在任意两个状态变化中,我们总能找到中间第三个状态,使两个状态到中间状态过程保持某一状态餐量不变。利用前面的实验定律,将状态、餐量联系在一起,都能够得到相同的结论,即一 定制量的某种气体,其压强于体积的成级与热力学温度的比值应该是一个与所处状态无关的常量。现在你肯定在想,这个比值常量是多少呢?它与什么有关呢?为此,我们最好先从一些特殊情况入手,这也是一种常用的科学研究方法。 实验表明,在标准状况下,益木尔的任何种类气体的体积都是二十二点四一四升。因此,将标准大气压一零一三二五帕于二十二点四一四升美摩尔的成级除以二百七十三点一五 k, 得到比值为八点三一交美摩尔 k。 这个数值称为气体长量,用二表示,上面是一木耳气体的比例,长量为二,那么 n 木耳的气体标准状况下,其体积为 n 乘二十二点四一四升,比值长量也就等于 n 二, 又因为这个笔直与气体所处的状态无关。那么结论就是,若气体的量为 n 摩尔,那么该气体任意状态的压强与体积的乘积,与热力学温度的比值等于该气体的摩尔数与气体常量的乘积。这一规律成为气体状态方程。 然而,最悲催的事实是,实际中没有一种气体能够完全符合上述气体状态方程,只有在压强不太大、温度不太低时,稀薄气体才与上述规律符合的较好。但重要的不是这个,重要的是在状态变化中,一切的不管哪一种气体的行为几乎都相同。 因此,我们有理由相信,这一方程代表了气体的根本性质。于是,我们把在任何温度、任何压强下都完全遵从上述气体状态方程的气体称为理想气体, 这一方程也就称为理想气体状态方程。下一步就是要解释这个规律,找出它与实际气体并不完全符合的原因。
103曲水大偉 01:01查看AI文稿AI文稿
01:01查看AI文稿AI文稿发明理想气体状态方程的人真是个天才,我们先来看看方程中的屁代表压强, b 代表气体体积, n 代表气体的物质的量,二代表摩尔气体长数, t 代表温度。我们对方程进行改写,就得到了较为直观的表达式, 第一是理想气体的威力,数越多,体积就越大。第二,温度越高,气体体积越大。第三,压强越大,气体体积越小。我们会发现,只有粒子数、温度和压强三种因素可以影响到理想气体的体积。那么在化学上,气体体积和木耳质量之间又有什么关系呢? 我们只需要把方程做一个简单的变形,就会得到一个神奇的柿子,其中的体积就等于质量除以密度,物质的量就等于质量除以摩尔质量。因此,在同温同压下,两种气体的摩尔质量之比就等于密度之比。 得出结论后就非常简单了,随便来道题均可秒杀。在标准状况下,不管是什么气体,他们的密度之比一定等于摩尔质量之比。
7.7万地球小视 00:35查看AI文稿AI文稿
00:35查看AI文稿AI文稿有个方程,高一老师想等高三老师讲,高三老师以为高一老师已经讲过了,他就是理想气体方程,也叫克拉伯龙方程。同温同压下,阿维实数定值。所以相同物质的量的任何气体 体积都相同,这就是阿福加德罗定律。物质的量等于质量比,摩尔质量,质量比,体积等于密度。所以同温同压下,摩尔质量之比等于密度之比。比较气体密度时,直接比较摩尔质量大小。
2542Diors.嗨nine 05:02查看AI文稿AI文稿
05:02查看AI文稿AI文稿上个视频咱认识了理想气体,他在任何温度、任何压强下都遵从气体实验定律,也就是这三条定律对应的分别是等温、等容和等压变化。 那如果温度、体积和压强这三个餐量都发生改变,能不能总结出一个万能的关系?是啊, 来试试看。掏出一团一定质量的理想气体,他的变化过程如图所示,咱用 abc 表示其中的三个状态, 依次来分析从 a 到 b 的过程。温度不变复合波伊尔定律可以写成这样,再根据温度不变,再让等式两边分别处以相等的 ta 和 tb, 等式就依然成立。再看从 b 到 c 的过程,因为是体积不变, 所以满足查理定律可以写成这样。咱在左右两边分别呈上 vb 和 vc 这两个相等的体积,那等式依然成立。 发现没?这两组得到的关系适中,都有 pb 乘 vb 处以 tb, 那就可以连立起来。这个 b 状态其实就相当于从 a 到 c 的中间状态, 咱不妨把它省去。这样从起点 a 到终点 c, 就有这么一个关系式,与压强、体积和温度的变化都有关,他就是理想气体状态方程。 咱把其中的 a 和 c 换成一和二,用文字表述,就是一定质量的某种理想气体,再从状态一变化到状态二时,压枪跟体积的成绩与热力学温度的笔直保持不变,那咱也可以把公式写成这样, 其中的 c 是直,与气体种类和质量有关的常量,与压强、体积和温度都无关,明白了吧? 那这个公式该如何使用呢?举个例子告诉你,一定质量的气体初始状态 p 一、 v 一和 t 一的值以及末状态 p 二、 t 二的值。要你求 v 二,那你只要利用公式先变形,再带入数据,直接计算就行。这种题就不用我细说了吧? 但要提醒你一句,计算前一定要先确定是一定质量的气体才行啊。 下面研究有点难度了,咱在视频开头用这三条定律推出了理想气体状态方程, 反过来,他也可以印证这三条定律,比如温度不变时,就相当于波伊尔定律。那么灵活运用离 气体状态方程,或者说综合应用这三条定律就成了咱更高的目标。举个例子,一定智障的理想气体经历了如图所示的 abbc、 cd 和 da 四个过程,其中 bc 的延长线通过远点 cd 垂直于 ab, 且与水平轴平行, d、 a 和 b、 c 平行,则气体体积在如何变化呢?来分析一下。这是一个压强温度图,那么过远点的直线,也就是 b、 c 所在的直线,就应该是挡容线, 所以从 b 到 c 是等容变化。体积不变,看选项 b 说 b、 c 过程中保持不变就是正确的。回到图像, d、 a 与 b、 c 平行,那就也是等容变化了。你要真 这么想,可就被坑了,别忘了,这条线根本不够远点,那就不是等容线。要想分析,他应该分别过远点,做与 d、 a 有关的等容线。你已经学过,等容线斜率越大,气体体积越小, 那 d 所在的直线斜率大,所以从 d 到 a 体积减小,那选项 d 所说的 d、 a 过程中保持不变就是错误的。 然后咱再来看 ab 过程,显然温度没有改变,所以是等温变化,并且压强是减小的,那根据波伊尔定律,体积就应该增大,于是选项 a 所说的 ab 过程中不断增大就是正确的。 最后看 cd 过程,他对应的压枪不变,所以是等压变化,并且温度不断减小,那根据概率萨克定律, 体积也会不断减小。然而选项 c 说 cd 过程中不断增大,那就肯定错了。分析完毕,正确答案应该是 a 和 b, 明白了吧。 以上就是这个视频的全部内容,理想气体状态方程,反映一定质量的某种理想气体,再从状态一变化到状态二十,压强跟体积的成绩与热力学温度的笔直保持不变,可以表示为这两种形式。 利用这个公式,你可以直接带入数据去计算所求的参量,但是必须先确定是一定质量的气体才行。 另外,你也要理解,理想气体状态方程和这三条定律是互相印证的,所以在分析复杂的图像时,你要学会灵活的运用他们。怎么样都听懂了吗?听懂了就快去刷题去吧!
553玄鬒(zhen✔)子 05:02查看AI文稿AI文稿
05:02查看AI文稿AI文稿上个视频咱认识了理想气体,他在任何温度、任何压枪下都遵从气体实验定律,也就是这三条定律对应的分别是等温、等溶和等压变化。 那如果温度、体积和压强这三个餐量都发生改变,能不能总结出一个万能的关系式呢? 来试试看。掏出一团一定质量的理想气体,它的变化过程如图所示,咱用 a、 b、 c 表示其中的三个状态, 依次来分析从 a 到 b 的过程,温度不变符合波伊尔定律,可以写成这样。再根据温度不变,再让等式两边分别除以相等的 ta 和 tb, 等式就依然成立。再看从 b 到 c 的过程,因为是体积不, 所以满足查理定律可以写成这样,咱在左右两边分别乘上 vb 和 vc 这两个相等的体积,那等是依然成立。 发现没?这两组得到的关系适中,都有 p b 乘 v b 除以 t b, 那就可以连立起来。这个 b 状态其实就相当于从 a 到 c 的中间状态, 咱不妨把它省去。这样从起点 a 到终点 c, 就有这么一个关系式,与压强、体积和温度的变化都有关,他就是理想气体。状态。方程 三,把其中的 a 和 c 换成一和二,用文字表述,就是一定质量的某种理想气体,再从状态一变化到状态二时,压强跟体积的乘积与热力学温度的比值保持不变,那咱也可以把公式写成这样, 其中的 c 是直与气体种类和质量有关的常量,与压强、体积和温度都无关,明白了吧? 那这个公式该如何使用呢?举个例子告诉你,一定质量的气体初始状态 p 一、 v 一和 t 一的值以及末状态 p 二、 t 二的值。要你求 v 二,那你只要利用公式先变形,再带入数据直接计算就行。这种题就不用我细说了吧? 但要提醒你一句,计算前一定要先确定是一定质量的气体才行哦。 下面研究有点难度的。咱在视频开头用寨三条定律推出了理想气体状态方程,反过来他也可以印证寨三条定律,比如温度不变时,就相当于波伊尔定律。那么灵活运用理 理想气体状态方程,或者说综合应用这三条定律,就成了咱更高的目标。举个例子,一定质量的理想气体经历了如图所示的 a、 b、 b、 c、 c、 d 和 d a 四个过程,其中 b、 c 的延长线通过原点 c、 d 垂直于 a、 b, 且与水平轴平行, d、 a 和 b、 c 平行,则气体体积在如何变化呢?来分析一下。这是一个压强温度图,那么过远点的直线,也就是 b、 c 所在的直线就应该是等容线, 所以从 b 到 c 是等容变化。体积不变看选项 b 说 bc 过程中保持不变就是正确的。回到图像, da 与 bc 平行,那就也是等容变化了。你要这 这么想可就被坑了。别忘了这条线根本不够圆点,那就不是等容线。要想分析它,应该分别过圆点,做与 da 有关的等容线。你已经学过,等容线斜率越大, t t t g 越小, 那 d 所在的直线斜率大,所以从 d 到 a, t 就减小。那选项 d 所说的 da 过程中保持不变就是错误的。 然后咱再来看 ab 过程,显然温度没有改变,所以是等温变化,并且压强是减小的,那根据波伊尔定律,体积就应该增大。于是选项 a 所说的 ab 过程中不断增大就是正确的。 最后看 c、 d 过程,他对应的压枪不变,所以是等压变化并且温度不断减小,那根据盖里萨克定律, 体积也会不断减小。然而选项 c 说 cd 过程中不断增大,那就肯定错了。分析完毕,正确答案应该是 a 和 b, 明白了吧。 以上就是这个视频的全部内容,理想气体状态方程,反映一定质量的某种理想气体,再从状态一变化到状态二时,压强跟体积的乘积与热力学温度的比值保持不变,可以表示为这两种形式。 利用这个公式,你可以直接带入数据去计算所求的餐量,但是必须先确定是一定质量的气体餐箱。 另外,你也要理解,理想气体状态方程和这三条定律是互相印证的,所以在分析复杂的图像时,你要学会灵活的运用。他们怎么样都听懂了吗?听懂了就快去刷题去吧!
120励志中学生 01:07
01:07 01:22查看AI文稿AI文稿
01:22查看AI文稿AI文稿同学请按下暂停,认真读题。好,我们开始讲题。先复习一下理想集体状态方程的分态式的公式。 回去过后我们来解题。这是个打气过程,我们取打完气后的气体为总体对象,这打完气后,车胎内气体的压强为 p 二,空气的温度为 p 二,对应的分态式的式子为 p 二,乘以为比上 t 二。 我们在取车胎内原有的气体和打气时的部分气体作为分体对象,这每次打气的体积微,而他微打气前和打气中的温度均为 t 一。 那三十次打气对应分态式的式子应该为三十乘以 peadertv 比上踢打气之前,胎内器里的式子应该为 pe, 乘以为比 以上梯椅。那么运动理想气体状态方程列出完整的式子就是这样的。 好,最后我们带入数据,接得 p 二等于三点零六乘以十的五次方跑步卡。理想气体状态方程分代式在解决气体的分装问题和打气问题上非常简便, 一般基本上一分多钟就能拿到全分,希望同学能够掌握这种简便的方法。好,同学们再看一看,没有问题我们就下课吧!
73教物理的李老师 01:25
01:25 04:13查看AI文稿AI文稿
04:13查看AI文稿AI文稿现在我们来做一个对比实验,研究对象是注射器内的气体出胎体积起坐四十毫升,我们把小帽子戴起来, 我们压缩气体也好,拉伸这个气体也好,他的压强和体积的沉积,以热力学温度的比值是个长速,这个长速应该等于出态的压强乘四十毫升除以出态的温度, 现在我们把它的出台体积起做三十毫升,把小帽子戴起来,我们压缩气体也好,拉伸气体也好, 他的压强和体积的沉积也是一个常速,这个常速应该等于出胎的压强成三十毫升,所以出胎的温度,现在的体积小,常速小,刚才的体积大,常速大,刚才的体积大,气体的质量多,现在的体积小,气体 质量少,说明这个常速与气体的质量有关。那么气体的温度、体积、压强和气体的质量到底是什么关系呢?今天我们就来行用理想气体的状态方程来推到这四个量的关系。 刚才的实验告诉们,理想气体的压强和体积的沉积,以热力学温度的比值是个长速,这个长速与气体的质量有关。今天我们就用理想气体的状态方程来寻找理想气体的温度、体积、压强和质量的关系。 要寻找这个关系,我们就假设把气体的状态由初态变成标准状态,那标准状态的压强呢?好,就是一个大气压,标准状态的温度 呢,就是零摄氏度,就是二百七十三开始度。标准状态的体积呢?一亩二七体为二十二点四三 n 木啊。气体呢,仅二十二点四三乘以 n 么啊 n 魔啊素如何计算呢?就用气体的质量来处以气体的木啊质量 好,这样我们就找到了理想气体的温度、体积、压强和气体质量的关系是,对于所有气体而言, 标准状态的压强都是一个大气压,标准状态的温度都是二百七十三开始度,标准状态摩尔理想气体的体积都是二十二点四升,所以对所有气体而言,这一项都是一样的,我们把这一项 成为普遍使用的气体含量,再乘以摩尔素,摩尔素就用气体的质量来处于摩尔质量。 这个规律最新是由克拉白龙推出的,所以把它叫做克拉白龙方程。克拉白龙方程的本质就是告诉我们理想气体的温度、体积、压强和质量满足这么一个关系。 好,后面我们将用这个克拉白龙翻城来处理气体的变质量问题。现在我们用克拉白龙翻城来探究气体的压强有哪些因素决定。大家看在克拉白龙翻城两边同城以热力学温度, 铜处于细体的体积,克拉伯龙方程就变成这个式子。大家看这一下 是摩尔素除以体积就是单位体积中的摩尔素。现在我们在分子分母上同乘于阿弗加德罗常速,阿弗加德罗常速呈上气体的摩尔素 就是分子总数,除以体积就是单位体积中的分子数, 再乘以热力学温度。好,我们把这一项叫做一个长速 k, 这一项就是单位体积中的分子素系为 n, 再乘以热力学温度。于是我们发现理想气体的压强由单位体重的分子素和热力学温度来决定。好今天的内容我们就学习到这里。
428高考物理林老师 01:00查看AI文稿AI文稿
01:00查看AI文稿AI文稿理想气理状态方程 pv 等于 nrt r 是一个常数,不用管他的两个变式。 pv 等于小 m 比大 m rt 及 p 大 m 等于 rt, 可以推导出十多个推论,其中最常考的是这四个推论。 第一个,同温同压下气体的物质的量之比等于体积之比。这个呢,适合做隔板类的问题。一个滑动的隔板,他间隔出来的两个部分,体积之比和物质的量之比是相同的。 第三个,同温同体积的情况,物质的量之比等于压强之比。这个呢,在我们做 kp 啊算平衡常数的时候能用到这个推论。 第四个呢,同温同压同体积的两种气体,物质的量相同,三同定一同啊。同温同压同体积才能确定物质的量是相同的,物质的量相同的,两种气体分子数也是相同的。大家。
224小蕾老师-高中化学 00:39查看AI文稿AI文稿
00:39查看AI文稿AI文稿太简单了,理想气体状态方程中的 r 是多少?先说结论, r 的值约为八点三一五。优秀的你肯定还好奇是怎么算出来的。我们知道理想气体状态方程为 p v 等于 n r t, 所以啊,等于 p v b n t 在标准状况下, p 为一百零一点三二五千帕, t 为二百七十三点一五 k 四十一。摩尔的气体体积为二十二点四一四乘十的负三次方立方米,那么可以计算出 r 的值为八点三一五。关注我,教你一些课本不讲的。
127化学太简单了!
猜你喜欢
最新视频
- 4055飞飞同学。







