如何用wps制作勾股定理动画
粉丝5290获赞4.4万
相关视频
 00:40
00:40 06:01查看AI文稿AI文稿
06:01查看AI文稿AI文稿探索千年数学文化,你了解勾股定理吗? 今天老师带你认识一个具有很多年历史的新朋友,勾股定理。 勾股定理呢,也叫商高定力,在西方称为必达格拉斯定理。我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为骨,斜边称为弦。 早在三千多年前,周朝数学家商高就提出了勾三股四弦五形式的勾股定理。后来人们进一步发现并证明了直角三角形的三边关系为 两直角边的平方和等于斜边的平方。 勾股定理的本质是直角三角形中边与边的一种等量关系,因此,勾股定理在考察计算问题的过程中呢,其实只有两种考察形式,一、已知直角三角形两边长,求第三边 立在直角三角形 abc 中,角 c 等于九十度, bc 等于六, ac 等于八,求 ab。 二、已知直角三角形中的一边长及另外两边的数量关系,设未知数列方程,求边长立在直角三角形 abc 中,角 c 等于九十度, bc 等于六, ac 加 ab 等于十八,求 ab。 注意,在利用勾股定理球直角三角形边长时,首先要确定斜边,在有多种情况时需要进行分类讨论。求解, 在直角三角形 abc 中, bc 等于六, ac 等于八,求 ab。 所以我们会发现,勾股定理其实是在直角三角形中用来计算编长的一种工具。 而勾股定理章节的不论哪一类考察题型,都是将勾股定理的两种考察方向放在了不同的实际情境中。 而我们只要掌握将实际问题转化为数学模型的能力,就可以将此类问题逐一攻破。勾股定理的证明方法很多,常见的是拼图的方法。用拼图的方法验证勾股定理的思路是, 一、图形经过胳膊拼接后,只要没有重叠,没有空隙,面积不会改变。 二、根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理, 一般以这种方法出现。方法一,四个三角形的面积加上 e、 f、 g、 h 的面积等于 a、 b、 c、 d 的面积乘以四乘以二分之一 a、 b 加 b 减 a 的平方等于 c 的平方 化。简可证方法二,四个直角三角形的面积与小正方形面积的和等于大正方形的面积。四个直角三角形的面积与小正方形面积的和为四,乘以二分之一 ab 加 c 的平方等于二, ab 加 c 的平方。 大正方形面积为 a 加 b 的平方等于 a 的平方,加二, ab 加 b 的平方,所以 a 的平方加 b 的平方等于 c 的平方。 方法三,梯形的面积等于二分之一 a 加 b 乘以 a 加 b, t 型的面积等于二倍的三角形 a、 d、 e 的面积加三角形 a、 b、 e 的面积等于二,乘以二分之一 ab 加二分之一 c 的平方化,减得正。 勾股圆方图是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,如图 分析减一图一中的大正方形的面积可以表示为 c 的平方,也可表示为 b 减 a 的平方加四乘以 二分之一 ab, 所以 b 减 a 的平方加四乘以二分之一, ab 等于 c 的平方化,减得 b 的平方减二, ab 加 b 的平方加二, ab 等于 c 的平方。 所以当角 c 等于九十度时, a 的平方加 b 的平方等于 c 的平方。二、 x 加 y, x 加二, y 等于 x 的平方。加三, xy 加二, y 的平方。 三、一题一、得 a 的平方加 b 的平方等于 c 的平方等于十三, b 减 a 的平方等于一,则二 ab 等于十二。 所以 a 加 b 的平方等于 a 的平方加 b 的平方加二, ab 等于十三加十二等于二十五。 记, a 加 b 的平方等于二十五。今天你有哪些收获呢?我们以后就可以用拥有千年历史文化 的勾股定理来做数学题了。
844冠之课微课定制设计零代码 01:47查看AI文稿AI文稿
01:47查看AI文稿AI文稿勾股定理是初中数学的重要内容,今天给大家分享一组动态图片,让你的课件更加形象生动。神奇的勾股数用来做课程导入,激发学习兴趣。 注水法讲解勾股定理解释两个小正方形面积之和等于大正方形面积。 勾股定理的证明方法很多,赵爽利用弦图通过图形的切割和拼接进行证明,也是我国古代常用的出入相补法。 欧基里德在几何原本中用等级变形也进行了证明,还有传说中的必达哥拉斯拼图正法,再来看 看几个应用势力吧!我们可以借助勾股定理做出长围根号二根号三根号五等等的线段,形成无理数海螺图。 也可以用同样的方法,在竖轴上画出表示自然竖的算数平方根的点。 还有做题时常见的蚂蚁爬行问题,比如长方体圆柱体表面的最短路径,还有台阶上的的最短路径。使用这样的图片来动态演示,就更容易让学生理解啦! 以上图片直接插入 ppt 放映即可动态展示, 像这样的动态图片还有很多哟!你还想要哪些数学动图?快来评论区留言吧!
325小畅老师 15:16查看AI文稿AI文稿
15:16查看AI文稿AI文稿我们知道啊,在直角三角形中,直角边的平方和等于斜边的平方,这就是勾股定理, 这条直角边的平方呢,就等于这个正方形的面积,也就是这个绿颜色正方形的面积, 这条直角边的平方呢,就等于这个正方形的面积,也就是红色正方形的面积, 这一条边的平方呢,就等于这个大正方形的面积。我们看一下这个正方形的面积,如果这样变形一下,那么这个图形的面积跟这个 正方形的面积大小是有什么关系呢?大小是一样的,这是等级变形, 这也是等级变形,这是平移,同样的道理,我们可以把这一部分也变形到这里, 这就说明这个正方形的面积加上这个正方形的面积,就等于这个正方形的面积,这就验证了勾股定理。 这个动画是怎么做出来的呢?我就再做一遍 文件,文档选项,新建业,空白业,确定 上一页,把这个复制过去, ctrlc 复制 下一页,看着微粘贴,先做一个正方形 正方形, 按着上档键,箭头工具, 选中这条边。构造终点,选中这一点,这一点,还有这一点,构造圆上的弧, 选中这个自定义工具,选中这一点。 箭头工具。那么这个三角形呢,就是一个直角三角形 标记工具, 直角符号箭头工具, 把这个壶隐藏显示隐藏 全选显示现行中等, 选中这一点,还有这一点,变换标记项链 空白处,单机,选中这一点,再选中这一点。变换平移 平移,选中这一点,再选中这一条边。 构造垂线,把焦点点出来,焦点 跨转这一条直线,显示 隐藏 多边形工具, 制作一个四边形, 再制作一个无边四边形箭头工具。 把这一点移动到这里,把这一点移动到这里,这一点移动到这里。这一点呢?移动到这里。 编辑操作类按钮移动确定。 单机 这两点不动。这两点呢?移动到这里,把这一点移动到这里,把这 点移动到这里。这一点还在这里,这一点呢还在这里。编辑 操作类按钮,移动,确定 这个变形就做好了。 现在是把这个两个点往下平移, 单击这一点,再单击这一点,变换标记项链,单击 这一点,变换平移 得到了这一点,现在呢是这一点在这里不动。这一点呢?在这里也不动。 这一点呢?移动到这里,这一点呢?移动到这里。编辑操作类按钮移动,确定。 观察一下平移的对,然后再把这个图形平移到下方,也 就是把这个点移动到这里,把这个点移动到这里,把这个点呢移动到这里,把这个点移动到这里。 编辑操作类按钮,移动,确定 这个变形就做好了。选中这四个按钮, 这选择方法是有顺序的。编辑 操作雷按钮系列,依次执行这里,每个动作之间停留零点三秒, 这个时间你可以自己选确定试一下。 可以啊,再倒着算这几个按钮。 编辑操作类按钮系列, 以此执行。每个动作之间暂停 零点三秒,确定,单击。 很好,这个方法就做完了。 再做这个动画, 把这一点移动到这里,把这一点移动到这里,把这一点移动到这里,把这一点移动到这里。 编辑操作类按钮移动,确定。 单机 单击这一点,再单击这一点,变换标记项链, 单击这一点,变换平移平移,这一点呢就移到了这里, 把这个正方形给它变形一下,这一点不动,这一点也不动, 这一点呢移到这里,这一点移到这里,边际移动 确定,我们试一下 这个变形可以, 下一个变形就是这一点在这里不动,这一点在这里不动,这一点呢移动到这里,这一点移动到这里, 编辑移动,我们试一下可以, 接下来就该把这个图形向下偏移, 这一点移动到这里,这一点移动到这里, 这一点移动到这里,这一点移动到这里。点击操作类按钮移动确定 可以,然后依次选中这四个按钮,编辑 系列依次执行,每个动作之间暂停零点三秒确定,然后再依次选中 这四个按钮,在转中的时候是有顺序的,编辑操作类按钮系列,依次执行, 零点三秒确定, 试一下 可以,然后把这所有的店都隐藏了, 在空白处单击点工具,嗯, ctrla 全选, 显示隐藏点 显示, 单击这一点,显示隐藏 右键颜色 绿色,右键颜色 红色, 这个动画就制作完了。
128数学小视频 00:59查看AI文稿AI文稿
00:59查看AI文稿AI文稿如果数学可以这样的话,先画一个边长分别为 a、 b、 c 的直角三角形,再复制变形,正好可以得到一个边长为 a 加 b 的正方形,并且它的面积为 a 加 b 括号的平方。 因为角一加角二等于九十度,角三又等于角二,所以角一加角三也等于九十度,角四为直角。 由此我们得到中间是边长维 c 的小正方形面积维 c 的平方。因此小正方形加上四个直角三角形的面积正好等于大正方形的面积。左边展开,右边化解,消除相同部分, 我们就得到了勾股定语,你看懂了吗?
254大熊老师(小学数学思维)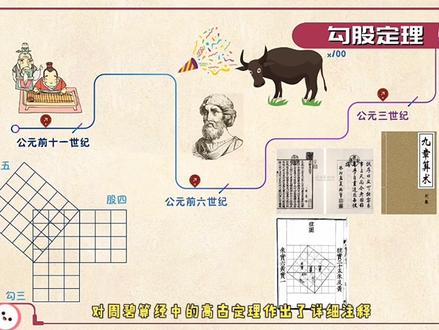 03:00查看AI文稿AI文稿
03:00查看AI文稿AI文稿今天我们来讲一下勾股定理。勾股定理是一个基本的几何定理,只在直角三角形中两条直角边的平方和等于斜边的平方。 为什么把这个定理叫做勾股定理呢?在中国古代,称直角下角型为勾股型,并且直角边中较小者为勾, 以长直脚边为骨,斜边为弦,所以称这个定理为勾股定理。公元前十一世纪,周朝时期的商高提出了勾三股四弦五的勾股定理的特例, 但是他没有把它证明出来。直到公元前六世纪,希腊数学家必达哥拉斯证明了勾股定理,因而西方人都习惯的称这个定理为必达哥拉斯定理。相传他发现勾股定理后高兴异常,命令他的学生宰了一百头牛来庆祝这个伟大的发现,因此勾股定理 又称为百牛定理。当然我国的数学家也并不示弱。公元三世纪三国时代的赵爽对周璧算经中的高古定理做出了详细注视记录,于九张算术中,高古各自成并而开,方除之及贤。赵爽创作了一幅高古元芳图, 用行数结合得到方法,给出了勾股定理的详细证明。接下来我们来看一下赵爽勾股定理的证明方法。这张图是周必算金钟的一页,这个图形太过复杂,我们把格线去掉来看一下。 在这幅勾股元芳图中,以弦为边长得到正方形 abde 是由四个相等的直角三角形再加上中间的小正方形组成的。每个直角三角形的面积为二分之 ab, 中间的小正方形边长为 b 减 a, 其面积为 b 减 a 的平方,于是便可得如下的式子,四乘二分之 a, b 加上 b 减 a 的平方等于 c 方。 化解后便可得 a 方加 b 方等于 c 方。当然,远在美国的加菲尔德同样也挣出了这个定理,由于在他证明出此结论的五年后,成为美国的第二十任总统,所以人们又称之为总统政法。那么他是怎么挣的呢? 在直角梯形 abde 中,角 aec 等于角, cdb 等于九十度,且三角形 aec 全等于三角形 cdb, a, e 等于 c, d 等于 b, c, e 等于 b, d 等于 a, a, c 等于 b, c 等于 c, s 三角形 a, e, c 等于 s, 三角形 c、 d, b 等于二分之 a, b, s 三角形 a、 c, b 等于二分之 c 方 s, a, e, d, b 等 二分之 a 加 b 乘 a 加 b。 因为 s, 三角形 aec 加上 s, 三角形 cdb 加上 s, 三角形 acb 等于 saedb, 所以二分之 ab 加上二分之 ab 加二分之 c 方等于二分之 a 加 b 的平方,所以 ab 加上二分之 c 方等于 ab 加上二分之 a 方加 b 方,所以 c 方等于 a 方加 b 方。以上就是高普定理的两个证明方法了,你学到了吗?
461疯狂数学 00:23
00:23
猜你喜欢
- 1.0万甜甜圈
最新视频
- 2.1万晋赫子硕











