将军饮马牧民饮马15-5 #我要上热门🔥 #最短路径问题
初二牧民饮马怎么画
42
7
35
10
举报
发布时间:2025-11-20 11:24爱讲大道理的拖堂天王
粉丝1.1万获赞4.2万
相关视频
 05:05
05:05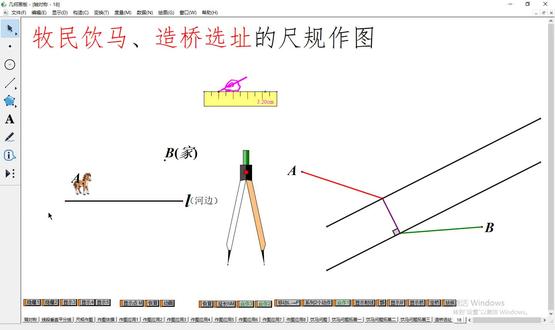 07:37
07:37 02:17查看AI文稿AI文稿
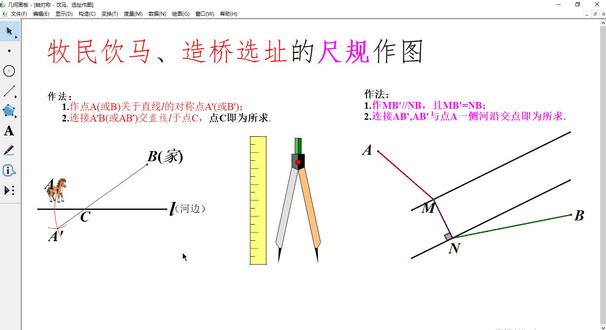
02:17查看AI文稿AI文稿但是八年级一道再看似乎无从下手的题目,已知 p q 是锐角 a o b 那两点 分别在 oaob 上求做点 m n, 使 p m 加 m n 加 n q 最短。 在遇到难题的时候,有一个小技巧,就是找当前学的知识点。就比如这道题出现在我们学对称轴的时候,那么我们就要利用对称轴来解这道题, 这道题也被称为将军一马。我们以 oa 为对称轴,做点 p 的对称点批撇, 以 o b 为对称轴,做点 q 为对称点 q 撇。 这个时候就会发现,不管 m 在 o a 上,两边 p m 都等于 p 撇, m n 也一样,那么 p m 加 m n 加 n q 就可以换为 p p m 加 m n 加 n q 撇连接 p 撇 q 片, 那么 m n 就是 p 撇 q 撇与 o a o b 的交点, 因为两点之间线段最短,连接 pm 连接 q n 连接 m n, 那么这道题就解出来了。请问我讲明白了吗?如果觉得我讲的好的话,请给个免费的小心心吧!
62子谦学物理
猜你喜欢
最新视频
- 2071小阳醒醒
















