淘宝上怎么搜乐诺三角形钻头
粉丝2391获赞2.3万
相关视频
 01:12查看AI文稿AI文稿
01:12查看AI文稿AI文稿你知道用什么方法可以在物体上算出一个方口吗?落落三角形原理制作成的钻头可以轻松算出一个正方形的孔。从等边三角形的顶点分别绘制以边长为半径的圆,三个圆相交的部分就是一个落落三角形,其最大的特点就是在旋转时具有恒定的宽度。 从视频中可以看出,乐乐三角形与平行线接触,并始终保持在平行线内,这也证明了无论方向如何,乐乐三角形旋转时和圆形一样宽度都是恒定的, 因此他们像圆一样顺畅的滚动,但他在旋转时至今却在发生着移动。我们可以看到他的至今的运动路径形成了一个波浪状的图案。 当三角形在正方形内旋转时,他能够保持在正方形内,并始终与正方形的所有四个边保持接触,但旋转轴不会固定在一个点上。工程师通过结合齿轮和 六六三九型的独特特性,设计出了转子发动机。转子发动机平稳的运转产生的震动非常小,与传统的发动机相比,重量轻、体积小、排量小、工艺大。 除此之外,乐乐三角形制成的井盖也被认为是除了圆形井盖之外,唯一一个不会掉进下水井里的井盖。所以在日常生活中,你们知道还有哪些用的是乐洛三角形呢?
23.7万有你科技 01:27查看AI文稿AI文稿
01:27查看AI文稿AI文稿我们都知道在机加工上,麻花钻可以用来钻圆孔,这个很容易理解,以圆形钻头为半径钻出来的肯定是圆孔。那如果我想机加工一个方形的孔该怎么办呢?这就用到了乐诺三角形原理。它是一种特殊的带弧度的三角形, 分别以正三角形的顶点为圆心,以其边长为半径做圆弧。由这三段圆弧组成的区边三角形称为乐诺三角形。 它的特点是在任何方向上都有相同的宽度,即能在距离等于其圆弧半径 a 的两条平行线间自由转动,并且始终保持与两直线都接触。 机械加工上,利用这个性质,把钻头的横截面做成乐诺三角形的形状,就能钻出方孔。你看明白了吗?有的朋友可能发 发现这个三角形旋转时有类似发动机的声音,大名鼎鼎的转子发动机也是根据这个原理发明出来的。
87优选好味道 00:16
00:16 05:44查看AI文稿AI文稿
05:44查看AI文稿AI文稿类似的这种形状啊,在生活当中就比较常见了啊。呃,我们暂且把它称作是改版的乐乐多变形啊。呃,比如说这个吉他的拨片,还有一些扫地机器人,哎,也做成了这种形状,但是严格来说就不能叫做乐乐三角形了,对吧?是改版的乐乐三角形,就是因为他 变得圆润了,不割手了。还有一些硬币啊,使用的就是改版之后的漏漏五边形或者是七边形啊,也很好看。哎,那小问题啊,硬币为什么不是其他的形状呢?你看绝大多数硬币都是圆的对吧?然后个别的是做成这个漏漏边形,这是为啥呢? 其实目的是和井盖是一样的,早期的目的呢,就是为了试用这个投币机,就是早期的投币机。我如何看你是否投入硬币了呢?就是通过检测这个硬币他的宽度,所以硬币的这个形状他必须得是等宽曲线啊,这样不管你怎么投是吧,我都能检测到啊。但是现在的投币机原理就不一样, 现在一般使用的就是这个震荡电路,然后检测你硬币的这个材质来分辨的。这块咱们就不多说了,所以等关曲线是不是只有勒路多边形呢? 是的啊,有无数种,至少我通过露露多边形,对吧?我就可以构造出无数种等关局限的就是我通过调整这个在外边跑的这个圆他的大小呗,对吧?那还有更一般的情况呢,我们使用一般三角形同 可以构造出等关曲线,那下面咱们来说一下具体的方法,比如说这是一个一般的这个三角形 abc 啊,那为了方便描述,我们假设这个边长呢?呃,分别是小的 abc。 那首先,我们先要将线段 cb 延长至地点,比如说这是地,这里呢,有一个要求,就是延长出来的这段线段啊,咱们假设是 s, 这个 s 呢,他要大于等于 a 加上 b 再减去 c 啊,一会你就知道为啥了。然后呢,我们以 c 点为圆心, c、 d 为半径画一段弧,交 c a 的延长线于一点。 再以 ae 为半径画一段弧,交 b a 的延长线与 f 点,再以 bf 为半径,画一段弧,交 bc 的延长线 预计点。为啥要求这个 s 要大于等于 a 加上 b 减去 c 呢?因为如果小于啊,这个焦点计就在 b c 上了。如果 s 刚好等于 a 加上 b 减去 c, 那么你做出这个等宽曲线呢,他就会有个尖点,哎,就是这个点 c, 你试一试就知道了啊。咱们继续再以 cg 为半径做一段弧啊,交 ac 的延长线与 h 点,再以 ah 为半径画一段弧啊,交 ab 的延长线与挨点。 最后以 bi 为半径画一段弧,交 cb 的延长线与这一点可以证明,这一点与地点重合。这个大图形就是一个等宽曲线了。 其实要想通比较容易啊,不过完整严谨的证明过程就比较繁琐了啊,咱们就不展开了。所以理论上啊,井盖做成这个形状也可以哎,不过那就有点不太美观了啊,而且不适合批量生产啊,还是原料最好。我们可以证明,在宽度相等 的所有等宽曲线当中啊,首先,他们周长是相等的了,这是八倍的定理。其次呢,面积最大的是圆啊,面积 最小的呢,就是乐乐三角形啊,这面积最大的是圆,对应的其实就是等周定理对吧,就是说周长一定的情况下什么样的形状面积最大呢?答案是圆啊,那面积最小的是乐乐三角形哎,这也是一个定理啊,叫做布拉斯科乐贝格定理啊, 这都是有严格证明的啊。不过呢有一个问题啊,到目前为止还没有结论,就是说如果我用等大的乐乐三角形来密铺,那么他的填充密度是多少呢?哎,这个问题没有结论啊, 就目前只是有一个最好的答案,就说填充密度约等于百分之九十二点二九啊,但是还没有证实,感兴趣的同学可以这个琢磨琢磨啊。那还有一个好玩的事啊,就是说如果我们在一个乐乐三角形里边啊,做一个最大的内切圆,然后再 外边呢做一个最小的外接圆啊,那首先他俩的圆心是同一个,其次呢这两个圆他的半径之和就是这个乐乐三角形他的宽度啊,好玩吧。嗯,那平面的说完了,你看他好奇三维的哎,说有没有这个乐乐四面体呢?有啊,构造的方法差不多就是使用三个球体啊, 同样你每一个球心呢,都要通过另外两个球体的表面啊,然后香蕉得出来的这个立体结构呢,哎,他就叫做勒洛丝命体啊。但是啊,这个勒洛丝命体呢,他并不是等宽的啊,就是他两个边缘之间呢差了那么一丢丢啊, 不过可以在此基础之上呢给他完善一下啊,就是让他变得圆润一些就好了啊。圆润之后的这个四面体呢叫做麦斯纳啊,麦斯纳四面体啊,呃,所以可能有人见过这个图哎,这就是麦斯纳四面体,就是就改变之后的这个勒罗斯面体啊,他就是等换的了哎,但是同样有一个未解之谜,就是在 所有等宽的立体结构当中,迈斯纳四面体的体积是最小的吗?人们猜测是的啊,但是没有证明就二维的已经解决了啊,三维的还没解决啊,总之还有很多好玩的地方。最后咱们再来说一个 说露露三角形呢,他可以在一个正方形里边去旋转啊,他可以覆盖百分之九十八点七七的面积,唯独这个正方形的这四个角他是不能覆盖的啊,不过这已经很好了,那么利用这个车型,人们就制作了方孔钻头啊, 原理就是我把钻头给它做成这个乐乐三角形的这个形状啊,但是要削掉一部分啊,就是为了让钻出来的这些碎屑啊就能跑出来啊,呃,这样呢,就可以钻出带有圆角的方形孔了啊。好吧,时间关系啊,今天咱们就唠到这,我是妈咪叔,一个交织的理工男,下期见,拜拜。
1913妈咪说MommyTalk 01:46
01:46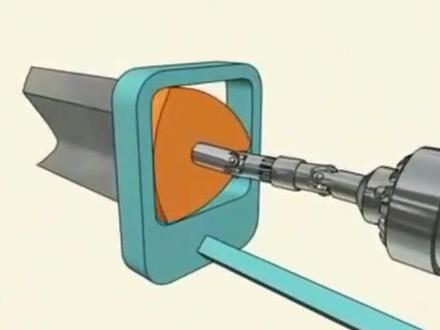 01:33
01:33 10:02查看AI文稿AI文稿
10:02查看AI文稿AI文稿之前我们提到过一个乐乐三角形,还记得吗?说,请问除了圆形还有什么形状可以作为这个下水道井盖它的形状呢?哎,乐乐三角形就是其中一个答案啊,就是这个形状。那妈咪说,知识就是力量,咱们今天啊,就来展开的唠一唠啊,什么是乐乐三角形啊,以及他有哪些神奇的地方呢? 咱们先回到开篇的这个问题啊,说,除了圆形还有什么形状可以作为井盖的形状?哎,有没有同学好奇过呀,说,正三角形不行吗?为啥非得是乐乐三角形呢? 你的理由可能是这样了,说呢,我在一个正三角形是吧,我任意取两点做一条线段啊,这条线段它的长度一定是小于等于这个正三角形它的边长啊。所以呢,假设说我们有一个这个正三角形的一口井,这个井盖呢,只要是做的比井口稍稍大那么一丢丢,哎, 那不管你什么角度把这个井盖往下放,这个正三角形的一条边他总会被卡住啊,因为他最长啊,所以理论上啊,正三角形作为井盖他也不会掉下去,这么说对不?不对,井盖还是会掉下去, 因为没人规定你这个井盖就是这一条边,他必须得横着往下掉啊,对吧,我可以把井盖给他旋转一下呀。啊,你比如说,呃,这,这是一条边,我现在给他竖过来,然后呢,这是另外的两条边啊, 那这就相当于现在你这个井盖它的宽度就是这个正三角形它的高了啊,然后你贴着这个井的一条边往下掉,那肯定是能掉下去啊, 前提是井盖与井口到形状相似,且呢,井盖只比井口大了一个无穷小啊,能明白这个意思吧?不行,你们在纸上剪一个这个正三角形啊,一试就知道了,所以正三角形不能当做井盖, 哎,那问题就来了,什么形状可以当做井盖呢?我们换一个视角啊,来看待这个问题啊,咱们脑补说假设呢,呃,有这么一个封闭图形啊,就什么形状咱们先不管,对吧?我们呢用两条平行线啊,去夹住它, 就严格的来说就是两条平行的 support 停了,那就是支撑线啊,说切线不严谨啊。然后呢,我们去旋转这个图形,哎,就是让他滚动起来,然后我们来看这两条平行线之间他的距离啊,能听明白吧?这就像你用这个油标卡尺去夹一个核桃一样,对吧?就你不停的换角度去测量这个宽度啊, 那同样我们夹出来的这个距离也叫做这个图形它的宽度啊,你比如说,呃,正三角形,如果你把一个正三角形放在一条线上,那此时它的这个宽度呢,就是这个正三角形它的高啊,但是如果呢,我把这个正三角形给它立起来, 哎,那此时他的这个宽度就是一条边长啊,这样你小的宽度就可以掉进这个大的宽度里。那什么形状可以当井盖啊,就是要求这个图形你无论什么角度去测量啊,他的宽度必须得是个定值啊,像这样的封闭曲线就叫做等宽曲线, 换句话说,只要是等宽曲线,理论上都可以当做井盖。圆形就是最普通的一个呀,所以几乎所有的井盖啊,都是这个圆形,所以开篇的问题呢就变成了,除了圆形还有什么样形状的等宽曲线呢? 呃咱们先来说一类啊,就是以乐乐三角形为代表的乐乐多边形啊,乐乐呢是十九世纪的德国那名工程师啊,就是他最早把这个乐乐三角形引入到了工程领域啊,因此被大众熟知了。呃,但是现在啊,有据可考的第一个发现乐乐三角形是等宽曲线的人啊, 并不是勒洛,而是欧拉啊,欧拉在这个一七八一年啊发表了一篇论文哎,就说,哎,这个图形好神奇对吧,你不管什么角度去测量啊,他这个宽度呢,都是一个定值啊,欧拉还给起了个名说叫 obiforms 啊。呃所以呢,如果我们还是用两条平行线去夹住一个勒洛三角形啊, 那么不管你这个乐乐三角形他如何的旋转哎,这两条平行线的间距就是不会变的。那怎么样去做一个乐乐三角形呢? 其实呢,就是用三个相同大小的圆形要求是呢,每个圆的这个圆心要落在另外两个圆上啊,这样你三个圆中间相交出来的这部分哎,这就是乐乐三角形了啊,或者呢,你可以用一个正三角形, 以其中一个顶点为圆心,以这个边长为半径,以对边为弦画这么一段弧,然后每 每个点都重复这么一次啊,由这三段弧组成的图形啊,就是一个乐乐三角形了,那知道怎么来的了,那那那面积和周长就好求了对吧,最笨的办法,那面积我就用三个扇形剪掉两个正三角形他的面积呗,我们假设这个大圆他的半径呢,这是一, 也就是这个正三角形,他的边长是一,那一个扇形的面积呢,就是六分之一大圆的面积,所以三个扇形呢,就是大圆面积的一半,也就是二分之派。那正三角形的面积是多少呢?边长是一,面积是四分之二三,对吧? 两个三角形,那面积就是二分之,根号三啊,所以乐乐三角形的面积啊,就是二分之一。提出来,然后是派,减去根号三,那写成更一般的形式,如果这个半径这是 r, 那面积 就是二分之一派,减去高二三倍的尔方。那咱们再来看周长,周长就很好求了,你每一段弧长呢,就是六分之一大圆的周长,一共三段,所以就是这个大圆周长的一半啊,也就是派,那再写成一般的形式,就是派尔。 你看这个 r 是啥呀?它不仅是这个大圆的半径,这个正三角形它的边长,它还是这个落落三角形,它的宽度。那我们这样,我们画两条平行线,让它的间距呢?是 d, 然后在平行线中间呢,我做一个刚好被夹住的乐乐三角形,那它的宽度就是 d, 对吧?那这个乐乐三角形它的周长是什么呢?那根据刚才的结论,它的周长就是派 d 啊, 圆周率乘以宽度。那如果我们在平线之间做一个圆,分别和这两条线相切,那这个圆的周长是多少呢?也是派的,也就是说他俩周长啊,相等。哎,这个结论就叫做芭比尔定理。 说的是呢,对于等宽曲线,只要他们的宽度是相等的,则他们的周长也相等。其实这个定理我们在之前给过一个证明方法,对吧?就是不分头变条,还记得吧?说呢,在等间距的这个平线上啊,头一条曲线 什么形状都可以,这条曲线与平行线产生的这个焦点数量的期望,只和曲线的总长度有关,和其他无关。所以如果我们投一个说直径等于这个平行线间距的圆,那不管你怎么投,一定产生 两个焦点。同样,我头一个宽度为间距地的落了三角形,也一定会产生两个焦点,你看产生焦点数量的期望相同哎,所以他们的周长也是相当的啊,能明白吧?那好,那下一个问题 说,这种等宽曲线呢,除了这个落落三角形还有啥呢啊?是不是说落落四五六七八这都有呢?不是,只有基数边的落落多边形, 也就说只有乐乐三角形啊,乐乐五边形,乐乐七边形,这么以此类推啊,构造方法是相同的,你比如说这是一个正五边形,我还是选一个顶点为圆心, 以对边为弦,画这么一段弧,依次这么重复,然后把所有的这个弧给他连接起来,哎,这就是一个 lolo 五边形了 啊,这有点丑啊。呃,以此类推,那就可以构造出落落七边形,九边形等等。所以什么是落落多边形呢?简单说就是在基数正多边形的基础上直接构造出来的等宽曲线,就叫做落落多边形。 有同事,啥叫直接构造啊?那还能间接构造吗?能啊,啥意思呢?我们以这个乐乐三角形为例啊,你会发现,其实这个图形啊,他长得不够圆润啊,用数学原来说呢,就是不够光滑, 说白了他只有三个尖,这三个点啊,我们说他是不可倒的,你比如说这点,我做左切线也能做出来,我做右切线呢,也能做出来,那如果我随便画这么一条线,他同样也是过这个点的,那这条线叫啥呢?严格来说就不 不能叫切线了,叫 supporting 了啊。行了,这不是我们关心的问题啊,总之所有的这个乐落多边形啊,他都不是光滑的,咱就都有个这个尖点,对吧?我们关心的是有没有办法能够让乐落多边形变得光滑呢啊?同时还能保持他是等宽曲线呢? 有啊,你比如说我们这样还是假设啊,这是两条平线,然后呢,我们让一个这个乐乐三角形在里边跑,我们在这个乐乐三角形的下边啊,给他放上一个圆,让这个圆呢,跟着他跑, 就让他俩始终保持有一个焦点啊,能想出来吧。然后呢,我在这个最下边,我再画一条平行线,那这两条平行线之间的这个间距就也是不会变的。哎,有灵感了吧。 其实这就相当于是我们让一个圆绕着一个乐乐三角形再跑,绕出来的最外边的这个边界,哎,就是一个定宽局限, 哎,大概是长这样。那为啥说他是光滑的呢?首先你这些个弧啊,这肯定是光滑的了,重点就是看这两个点他是不是尖点啊, 那我们就看他的左右切线是不是同一条。比如说看这点啊,他的左切线呢,就是以这一小段弧做的切线, 他应该垂直于这条线,对吧?他的右切线呢,就是以这个大弧做的切线,他也应该垂直于这条线。哎,左切线等于右切线啊。所以此处光滑,并且他整体还是一个等宽曲线。
3019妈咪说MommyTalk








