希望数学画板里面如何画抛物线
粉丝4001获赞1.8万
相关视频
 01:23查看AI文稿AI文稿
01:23查看AI文稿AI文稿如图,在平面内有一条定直线 l 和一个定点 f, 在直线 l 上任意选择一个点 h 连接 h f 构建终点, 过这个终点做 h f 的垂直平分线小 m, 再过 h 点做直线 l 的垂线与垂线小 m 相交,于大 m 点 连接线段 m f m h 设置 h 点。沿着直线 l 上下运动时, m 点跟着 h 点的运动而运动, 同时显示 m f 和 m h 的长度。会发现在 h 点不动时, m h 的长度和 m f 的长度都等于一点七六厘米。 点击动画, h 点开始运动时, m 也开始运动, m 点的运动轨迹就形成了抛物线。 同时也会发现 m h 和 m f 长度在不断改变,但他们长度始终相同。
276嘻嘻晓日记 02:16查看AI文稿AI文稿
02:16查看AI文稿AI文稿好,我们先打开几何画板,选择一条直线。 好,我们把直线上这两个点先把它隐藏起来, 再选一个定点 f。 好,我们这个定点 f 啊,给它取个名字啊。 好,我们在直线上取一点啊,我们记为 h。 好,我们选中这个 h 这个点。好,这条直线做它的垂线, 我们连接 h 和 f, 好,去构造它的终点。好,我们选中这个终点和这个 h f 这条直线做它的垂线。 好,紧接着我们连接啊,这里有一个焦点和这个 f 点。好,我们把 这个焦点我们记为 m。 好,下面我们来看这个 m 这个点的轨迹啊,它是受这个 h 的影响,选中点 m 和点 h 啊,来构造 m 点的轨迹啊。好,他就是一个抛物线啊,随着这个 h 点的变化,他在这个抛物线上移动。
126学数学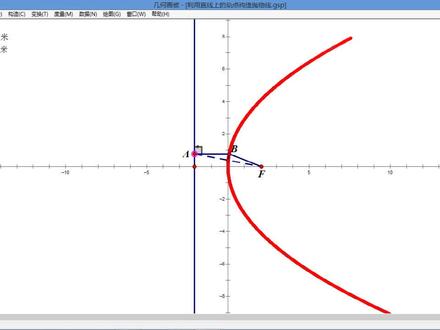 03:55
03:55 02:22查看AI文稿AI文稿
02:22查看AI文稿AI文稿抛线的绘制增加一页。 第一步使用线段直尺工具,按住上档键绘制水平线段 ab 线段直尺工具。 第二步在 ab 的上方绘制一个点 c 点工具。第三步在线段 ab 上绘制一个点 d。 第四步过点 d 做线段 ab 的垂线移动箭头工具,选择线段 ab 和点地,构造垂线。 第五步连接 cd 线段直尺工具, 选定旋转 cd 移动箭头工具,选定线段 cd 构造终点。第六步过点一做线段 cd 的垂线, 选中点一和线段 cd 构造垂线。第七步两条垂线的焦点为 f, 焦点为 f。 第八步选定点地和点 f 空白处单击点地,点 f 点地为主动点,它在线段 ab 上运动点 f 为随动点 构造规则空白处单机。 这就是一个抛线。
20数学小视频 07:17
07:17 04:34
04:34 08:13查看AI文稿AI文稿
08:13查看AI文稿AI文稿老师们,同学们大家好,今天我继续分享坐标系工具的使用方法,利用抛线图像解一元二次方程。 我们在遇到的一些数据比较大的医院二次方程的时候,我们 可能会希望得到一个正确的答案,快速正确的答案。但是呢,我们又觉得这个利用常规的方法去解它的过程比较复杂,计算比较多, 那么这时候就可以利用抛物线的图像来解一元二次方程,解出方程的解也可以验证你使用其他的方法解出的解是否正确。现在我就来分享如何利用抛物线的 图像解一元二次方程。我们首先建立一个飞狐参数版坐标系,两个参数我已经设定好了,现在点击鼠标左键,点击自定义工具, 找到一级彩蛋当中的经典坐标系,继续向后找到二级工具栏,飞狐直角坐标系参数版,匹配两个参数,第一个参数,第二个参数,现在坐标系就生成了, 让坐标初始化 好,我们这个数据啊,呃,可能比较大,我们稍微的 对他进行一个修改,把横坐标的坐标值我们改为五重坐标的坐标值我们改为,因为他最大的有一个是四千八,所以我们把它改成四百。 现在看这个坐标系的范围,四千八依然不够,那我们继续再把参数进行调整,我们调整到五百, 好,现在就有四千八这个取值了。现在看这样一个问题,说为了美化校园,某校计划在一块长六十米,中间就 花圃是长六十米,宽四十米的花圃,四周修建宽度相等的通道,设通道的宽为 a 米,也就是四周都是 a 米宽的通道。 第一位用含一的式子表示,通道和花坡的总面积就是整个举行的面积,我们重点看第二位,如果通道所占面积与花坡的面积相当,花坡的面积就是六十乘四十, 如果通道的面积与花坡的面积相当,那说明通道的面积也是六十乘四十,那整个巨型的面积就是六十乘四十的二倍。现在看这个矩形的长,他两边有两个 a 宽的通道,所以整个的长就是六十加二 a 宽度, 宽度就是四十加二 a, 那整个的面积就是六十加二 a 乘以四十加二 a, 然后说他的面积刚好和花圃的面积相等,也就是整个面积是花圃面积的二倍,那就是六十乘四十乘以二。就可以建立这样一个方程。 观察这个方程,明显发现它的数值是比较大的,我们需要化解,需要英式分解才能解得出来。那如何快速的把这个方程解出来呢?现在我们首先建立一个函数 数据,新建函数,找到方程 y 档,约我们输入框 号,六十加二 aa 就是一个变量,那么在结合画板的变量,只能以 x 的形式输入,所以找找 a 就要改成 x, 六十 加二 x 括号,这这个地方大家一定要注意啊,这个长他是不能直接产生的,如果你直接产生,你看这个后边这个括号,他是灰色的,就表示你输入不了, 那么这个地方一定要输入成号,成号就是这个新号成号。哎,现在你看括号的就变成黑色,是可以输入的啊,点击括号,然后四十加二 a, 四十加二 a 就是二 x, 好,这个方程就鉴定好了, 确定这个方程在这里,那现在我们继续利用匹配坐标系的方法来把这个函数的图像绘制出来,点击自定义工具,一级,一级工具,找到经典坐标系,找到二级工具 飞狐函数图像生成工具,点击鼠标放在这里 来,我们就发现这个函数的图像已经出现了一部分,那是因为,呃,左半轴的这个 坐标系不全,那我们稍微的进行一个调整,把坐半部分把它延伸出来。哎,现在就有了副伴奏,我们也可以调整出来,再放大一点。 好,现在就有了啊,纵轴也调整一下。那现在如何来求这个方程的减呢?那也就是要让这个函数与另外一个定函数六十乘四十乘二相等, 而六十乘四十乘二就是四千八,也就是说要与一条直线 y 等于四千八相交。那我们再建一个函数,新建函数,输入一个定函数,四八零零确定,点击 自定义工具,那就可以用这个方式来生成匹配坐标系的函数了,现在这两个函数的焦点的横坐标就是这个方程的结,我们找到 这两个焦点的横坐标, 选中这两个函数构造 焦点,焦点就有了焦点,而且处于雪种状态,现在我们只需要在度量,我们需要的是横坐标,在下拉菜单当中找到横坐标,那么这两个 点的横坐标就有了。一个是 k, 点是负六十, l 点是十,那就说明方乘六十加二 a 乘以括号,四十加二 a 括号等于六十乘四十乘二。这个方程有两个解,一个解十 x 等于负六十,一个解释 x 等于十,这和实际的解答答案是相符的,这样我们就把这个方程解出来了,再根据实际问题的意义对这两个方程的解进行符合实际意义的取值,就可以得到方程的解。 那么定这种办法,我们就需就只需要把方程列出来,甚至对方程都不需要化解,就可以直接利用函数的图像把方程的解求出来, 他可以作为一种验证答案是否正确的方式,你学会了吗?
10客舟听雨 00:36
00:36 02:24查看AI文稿AI文稿
02:24查看AI文稿AI文稿这是左边四个 x 的握手啊,把 f d r 四零点啊, f 点四零点掉到上面,画出直线 x 等于负四啊,直线 x 等于负四, 运动点 m 运动点 m 啊,暂时先把他固定在这位置啊,暂时他的这好, fd 先连起来。好,我们的一个自己就有了啊,那么另一个自己就是 坐一天。 好,下面我们在运动过程中的关键控制条件是要让两个智能相等相当好,那么怎么体现这两个智能相等,我们把这两个智能的建设以及方法摆在姿势上, 不能直接给他晒出来啊,假设当前的位置在这的时候,连麦一次就是五点八七,连到一次就得开始,因为老七, 好,现在我们让 m 解动起来啊,让你解冻起来,动起来的过程中保证这两个字是相等的啊,那么你可以看着这两个数据啊,看数据的变化啊,好,现在我们小小的动一下啊, 选中 m d 啊,好,在 m d 运动过程中 m f, m a 尺啊,长度发生变化,再使两个数据 看啊,他永远保持相等啊,永远保持相等啊,这样的运动点,哎,我会是出来的路径啊,怎么感觉啊, 这样的一种感觉啊,好,那么随着 m 点着运动时刻都是穿 ms 哈, ms 稍等,新出了这样的一个路径啊,这个路径 给人的感觉就和这个我们初中的我们的函数图像啊有点像,不过我们的图像 口齿有口臭的原因是我们把这个 f 体验 啊。
135蓝剑










