svm enable没有怎么办

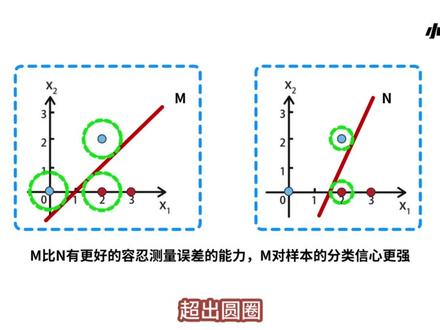
大家好，今天要讲的内容是 svm 支持向量机， 如果没有深度学习，可能现在依然是 s v m 的天下。也许 s v m 过时了，但不管怎么说， s v m 都是算法工程师必须要学习的常识性算法。 svm 是用来解决分类问题的，下面这个例子直接表明了 svm 分类器的特点。 假设在平面上分布着蓝色和红色两种样本， m 和 n 对应了两个不同模型的角色边界。直观来说，哪个模型更好一些？为什么 很明显， m 要比 n 看起来更好？因为对于 m， 即使样本在观测时产生了误差，但只要在绿色圆圈范围内，就不会影响最终的分类结果。 对于 n， 绿色圆圈很小，样本稍有变化，超出圆圈，分类器就会产生不同的结果。因此 m 比 n 有更好的容忍测量误差的能力。 m 对样本的分类信心更强。 s v m 就是要找到一个对样本分类最有信心的角色边界。 s v m 的角色边界。 各个样本的间隔 margin 是最大的，因此 svm 也被称为是最大间隔分类期。 例如分界面 m 和 n 都可以将样本正确的分开，这时将红色的分界面同时向左右两边平移， 到达与某个样本点相切的位置。此时在分界面的两侧就得到了两条平行的黄线，黄线之间的距离即为间隔 margin。 我们可以看出， m 是 large margin， n 是 small margin。 s v m 算法就是要找到间隔 margin 最大的角色边界， 而支撑这个间隔的样本会被称为支持向量，因此该算法得名支持向量机。 support vector machine。 无论训练哪种模型，例如感知器逻辑回归还是 s v m， 都需要先设计出模型的目标函数。 我们需要基于寻找最大间隔的分界面这一目标来设计 s v m 的目标函数。 下面就来详细的讨论 s v m 目标函数的推导过程。 设样本的特征项量为 x， 其中包含了 x 一到 x n n 个特征，每个特征对应的权重为 w 一到 w n 保存在项量 w 中， 因此得到决策边界的方程为 w， 一乘 x， 一加 w， 二乘 x， 二加到 w， n 乘 x， n 加 b 等于零。它的向量形式为 w 的转制乘 x 加 b 等于零。 设空间中有 m 个样本，第 i 个样本表示为 x i y i。 如果样本 x i 是正立，那么标记 y i 等于正义。如果样本是负立， y i 就等于负一。我们可以将第 i 个样本 预测值表示为 w 的转制呈向量 x i 加 b。 svm 将尝试寻找最大间隔的分界面 m， 而我们要将这个目标转换为具体的目标函数，进而设计出迭代算法。 设第二个样本 x i 到分界面的距离为 distance x i w， 其中 w 是分界面的参数。 在全部样本到分界面的距离中有一个最短的距离，我们设它的长度是 d， 而间隔 margin 就等于二 d s v m 就是要求出在所有 样本正确分类的条件下，使 margin 等于二 d 最大的分界面参数 w。 根据空间中点到平面的距离公式，可以将第 i 个样本 x i 到平面 m 的距离 distance 表示出来， 它等于将第 i 个样本的预测值 w 转制成 x i 加 b 取绝对值，然后除以平面的法相量 w 的膜。 因为 d 是样本到分界面最短的距离，所以对于任意的正立 y i 等于一，他们到分界面 m 的距离都大于等于 d， 而任意的负立 y， i 等于负。一到分界面 m 的距离都小于等于负地， 我们将不等式的两边都除以距离 d。 然后将平面的发向量 w 的膜和距离 d 相乘的结果看作是一个常数。 接着将不等式左侧的分子和分母同时除以该长数，就会得到新的参数 wd 和 bd。 此时相当于对所有的参数 w 和 b 都缩放了相同的长度。 接着对于圆分界面 w 的转制乘 x 加 b 等于零，同时令该等式的两边除以靶向量 w 的模和距离 d 的乘积，这会使该 分界面的参数进行相同比例的缩放。因此，我们将 w 和 b 的右下角标记一个 d。 缩放操作不会改变分界面本身，但可以使分界面和两条间隔边界线的参数保持一致。 我们将 w， d 和 b， d 的名称重新修改为 w 和 b， 得到所有正样文满足不等式一，负样文满足不等式二。 另外，恰好在分界面的黄色间隔边界上的正样本的代入值是正义，负样本的代入值是负义。 接着将间隔边界上的样本的预测 值正负一再带入到距离公式中，就会得到最短距离 d 等于法向量 w 的模分之一。 因此我们推导出 margin 等于二倍的 w 模分之一。而为了使 margin 最大，就是要使 w 的模最小。 求间隔麻疹的最大值等价于求模的平方的最小值，再根据模的计算公式展开，就可以得到二分之一倍的 w 的转制成 w。 另外，由于全部样本都会被预测正确， 因此预测值和真实值的符号是一致的。在正负样本满足的不等式的两边都乘以标记值 y i， 就可以得到一个合成的约束条件。 最终总结出 svm 算法的目标函数为，在满足所有样本的真实值乘上预测值大于等于一的情况下求出使 w 转制乘 w 取得最小值时的参数 w 和 b 的值。 说。平面上有四个样本，每个样本有 x 一和 x 二两个特征。样本的坐标 腰围零零、二二、二零和三零。其中蓝色圆圈是正例，红色叉子是负例。 我们要基于 s、 v、 m 的目标函数求出直线方程中的 w 一、 w 二和 b 三个参数的值。 首先，将四个样本点带入到约束条件中，可以得到四个不等式， a、 b、 c、 d。 例如，将复利 a 零零带入，得到复 b 大于等于一。 接下来要基于这四个不等式求二分之一 w 一的平方加 w 二的平方取得最小值时参数 w 和 b 的值。 将 a 和 c 连例得到 w 一大于等于一， b 和 c 连例得到 w 二小于等于负一。 很明显，在 w 一等于一， w 二等于负一的情况下，带优化的函数会取得最小值一。 然后将 w 一等于一和 w 二等于负一，重新带入到四个不等式中，可以求得 b 等于负一。因此就得到了平面方程 x 一减 x 二减一等于零。 从计算的过程中可以发现，实际上只有 a、 b、 c 三个样本对应的不等 是参与了运算，所以他们是支持项量。另外还可以计算出 margin 的长度，它等于 w 的模分之二，等于根号二，也就是一点四一四。 在刚刚的例子中，我们手动计算了 s v m 的结果。实际上，如果要用算法求解 s v m， 还要有如下三个关键点， 一、拉格朗日成资法和 k k t 条件。二、 s v m 的等价问题和队友问题。三、队友 s v m 的化解和计算 通过一系列的数学推导，我们可以得到一个只关于拉格朗的橙子 alpha 和 s v m 最优化函数。在该函数中，只有参数 alpha 和需要满足的条件。 该最优化函数说明了，如果我们有 m 个样本数据，那么就有 alpha。 一到 alpha m 这些参数，其中解除的 alpha 需要大于等于零，并且所有 alpha 与样本标签 y 相乘，再相加的结果是零。 当解说 offer 后，再根据 k k t 条件就可以计算出参数 w 和 b 了。 那么到这里， s v m 支持下 向量机就讲完了，感谢大家的观看，我们下节课再会。

恩施最孤独的小区啊，你们知道是哪里吗？没错啊，就是我身后的一电院小区，可能钓鱼的朋友知道啊，其他的可能知道的不怎么多。看到没有，你家门口两个大狮子啊，然后给你镇守家门， 咱们在小区里面看一下情况啊，然后这个小区的话就是物业费的话是七毛到九毛五之间这个样子啊，所以物业费也还比较便宜，毕竟老的金四房嘛， 就这种，他算是就是就是等一下这个小区啊，就他是一个经济盛房，然后停车的话都是在地面啊，就是这个肉眼可见他没有什么 小区环境啊，但是停车嘛，还是有点方便的了。然后视野啊，视野真的周边还是特别好，特别舒服，但是周边没 有其他的这样一些房子啊，啥都没有啊，就真的是最孤独的一个小区啊，但是干什么事啊？哈哈哈哈， 我记得上次我们来拍过，这边有一套差不多三千多的房子啊，然后最后也是没卖掉，因为呃税比较高嘛，你像这种经济适用房，反正呃税的话都要再超过，最起码都要个五六万这个样子啊。对的对的。