钟面表动角万能公式
粉丝10.8万获赞43.9万
相关视频
 02:28查看AI文稿AI文稿
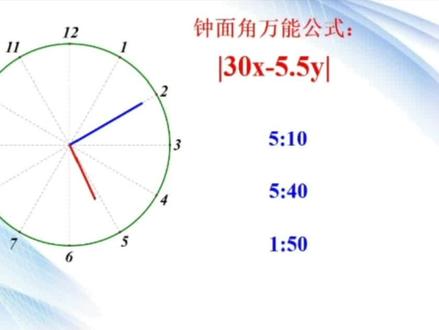
02:28查看AI文稿AI文稿哇哦,我不装了,我摊牌了。其实中面角有一个万能公式,就是这个三十, x 减去五点五倍的,我爱数一个绝对值。 这里的 x 指的就是十, y 指的就是分,以五点十分为例,那么 x 就是五, y 就是十。直接套公式,五点十分,时针与分针的假角就应该是三十乘以五减去五点五乘以十, 做一个绝对值等于一百五十减去五十五绝对值,那就等于九十五。其实这个公式一点都不神奇,稍微解释一下你就懂了。 五点整的时候,分针恰好在十二处,时针恰好在五处,因为每一小格是三十度,五点整有五个小格,所以三十乘以五就是两针。在五点整时初始夹角。我们又知道,分针每分钟转过六度,时针每分钟转过零点五度。如果这个还不会, 可以去看前面的视频。换句话说,分针每分钟比时针多走了五点五度,又或者说,分针每分钟可以追时针五点五度。 所以从五点到五点十分,时针被分针追了十分钟,那就被追了五点五乘以十分钟,所以我们用初始的夹角一百五减去被追过的角度,五十五度就是最终的结果。 为什么一定要竖绝对值呢?我们来看五点四十,五点四十。按照刚才的推理,我们可以先来算,五点整,五点整两针,夹角就是三十乘以五,时针被分针追了四十分钟,也就是追了五点五乘以四十,减去五点五乘以四十。 好,这样的话呢,是一百五减去两百二。哎,这里是负角度,所以我们要竖一个绝对值,确保角度为证,这里就是七十,演示一下五点四十确实是七十度,这个你可以自己去验证。 为什么要加取对值?是因为从五点到五点四十分,针已经越过时针了。这个公式还有一点小瑕疵,比如来看一点五十,一点五十,按照公式,此时两针夹角就应该是三十乘以一,减去五点五乘以五十, 再竖一个绝对值,应该点于三十,减去两百七十五,竖一个绝对值,那就是二百四十五度。我们知道二百四十五度其实指的是这个角,而我们指的中面角通常都是小于一百八的, 我们要求的是这个角啊。所以我们最后还要做一步,我们用三百六十度减去刚才求出来的两百四十五度,那就是一百一十五度,这才是答案。所以做一个总结啊,我们主要关注这个结果到底是不是大于一百八,我们就要用三百六十度去减,如果没有超过一百八,那就是这个公式,你捂了吗?
7857江苏初中数学老王 03:22查看AI文稿AI文稿
03:22查看AI文稿AI文稿daddy 妈咪爱的北鼻,今天来看到什么题?来,咱们今天来看一道与大家生活息息相关的中面角的计算问题啊,看看这种题大家会不会算啊?来问你九点二十五分的时候,时针和分针的夹角是多少度?来 给大家画出图来了啊?九点二十五分,那有些同学就会问啊,老师,你说这个夹角,你是说这个夹角啊?是这个夹角,这是不是俩夹角啊? 那我们通常指的这个夹角啊,我们通常指的这个夹角是指他小于等于一百八十度,也就是小于等于平角的那个度数啊,所以说,在这个题当中,他的夹角是不是就是这个呀? 啊?小于等于一百八十度,好,那这个角度是多少度?我们该怎么求啊?啊,这种题啊,咱们分两步啊 啊,咱们先算整段的度数啊,再加上分段的度数, 那就是他们的夹角的总的度数了,那什么叫整段的度数?来,咱们来看啊,整个这个表盘是个圆形,对吧? 圆周是不是三百六十度?圆周是三百六十度,我们现在平均是不是分成了十二份呢? 是不是十二段?那每一段他的度数是多少?很明显了,是不是三百六十度除以十二,是不是每一段都是三十度啊?是不是他一小时走三十度,他一个小时是六十分钟,那是不是每分钟他走零点五度呀? 对吧?这是十针走的度数,那分针呢?那分针一分钟走多少呀?分针咱们说了啊,从九点到 十点的时候,好,九点的时候分针在这来转一圈,转一圈,是不是转到十二的时候,这是不是转了一个小时啊?转了一个小时,他是不是转了三百六十度啊?转三百六十度,那他一分钟走多少?是不是三百六十度?除以他这个六十分钟啊?也就是说 分针是不是一分钟走六度?好,时针和分针每分钟他转的度数我们求出来了,我们看看这个题该怎么做啊?先算整段,再算分段,咱们先数数这个夹角有几个这种整段。咱们从这看, 他现在是不是指到五这个位置啊?五到六是不是一段,六到七,两段,七到八,三段八到九,这是不是四段?也就是说他现在这个夹角是不是有四个诊断呀?那一个诊断是不是三十度?四个诊断是不是这一百二十度啊?好,咱来看这个 分段。分段是啥意思?也就是说咱们之前咱们九点整的时候,咱们的时针是不是在这个位置?他现在转到了九点二十五,是不是转了这么一个角度? 这不够一个整段吧?那不够一个整段,咱看看这一小段他到底是转了多少度啊?刚才咱们说了,时针一分钟是不是转零点五度啊?他现在转了多少分钟?是不是转了二十五分钟啊?也就是二十五要乘以这个零点五度呀, 对吧?好,咱们算一下啊,一百二十度加上十二点五度等于多少?等于一百三十二点五度。 好,所以说九点二十五分的时候,时针和分针的加角是多少?是一百三十二点五度。好,今天教给大家这个方法听明白了没有?听明白了,给张老师点点关注啊!今天的课咱们就上到这下课喽!
5367战老师开课了 04:13查看AI文稿AI文稿
04:13查看AI文稿AI文稿中面角问题是初中必考题型,从初一开始就考,而很多同学到了初三还不会,今天小杨老师教大家一个公式,秒杀所有的中面角度问题,来思考下图中面角是多少度。首先我们知道时间是一时十五分, 想要知道时针和分针的假角,需要找到一个参照的角度, 我们每次都找十二点这个角度看起来会方便一些。那这样子我是不是就要用三针走的这个角度,再减去十针走的角度就可以了吧? 想要知道分针走的角度的话,那我需要知道分针的速度以及时针的速度。好,速度大家讲,分针 一小时走了整个一圈,一圈是三百六十度,一小时是六十分钟,最分针的速度是用三百六十度除以六十分钟, 等于六度每分钟。而时针呢,一小时只走了一大格,大家想想,在时钟里面一共有十二格,三百六十度除以十二,所以每格是三十度,那时针就是三十度, 用了一小时除以六十分钟,那等于零点五度每分钟。 好,有了时针和分针速度之后,那不就好算了吗?分针十五分,使用十五乘以 六度,最分针走的角度是九十度,减去时针他走了是一小时,再加上这个十五分钟,那一小时他是不是走了三十度, 再加上十五分钟,他每分钟走了零点五度, 他就等于三十度,加上七点五,三十七点五。好次是加脚 用九十度减去三十七点五度,等于五十二点五度,这就是一时十五分,时针和分针的夹角。有人说,小王老师,你刚刚不是教我用一个公式吗?我 这个图画起来感觉也挺麻烦的。好,现在我们就把公式给大家罗列出来。你想要求出公式,还是要知道时针和分针走的速度,这两个是很关键的。那我们先假设时间是 x 十 外分,要算出 x 时外分,时针和分针的夹角。刚不是说吗?时针和分针形成的夹角,是用分针的度数减去时针的度数, 是吧?是用这个角度减去时针的。哎,或者有的时候我的时针是不会跑到下面来,那时针会跑到这边来,那不就会变成用时针的度数减去分针的度数了吗? 没有关系,我们可以先把他们两个度数表示出来。来,时针他是走 走了, x 十外分,那他 x 十的时候从十二点走过来,他是用 x 乘以三十吧, 再加上外分,他每分钟走零点五,外乘以零点五吧,这是十针三十, x 加零点五万, 而分针呢,直接是六万。那接着不知道用分针减十针还是用时针减分针,直接套个绝对值,最夹角就是绝对值 三十, x 减五点五 y。 同学们,这个公式可以解决所有的中电夹问题,你哪怕不会画图,直接用公式也可以,你学会了吗?
1165大静和小洋老师 03:17查看AI文稿AI文稿
03:17查看AI文稿AI文稿一分钟学数学,今天我们来学习一下七年级中面角计算的问题。首先我们先了解一下时针和分针转动的过程。时针的转动速度慢,分针转的比较快,时针转一圈需要十二小时, 一小时是六十分钟,所以它的转动速度就是三百六或七十七百二零点五度每分钟,每小时呢就是转到三十度,所以就三十度每小时。分针呢转一圈需要六十分钟,那的转动速度就是六度每分钟。结合分针和时针的转动速度,我们通过一个具体的例子来研究一下正面角的计算步骤。 不管是几点几刻,我们都以十二点为起点,分针大概转动了这么多,每分钟走六度,所以是六乘以三点八。时针大概转动了这么多, 是两小时,所以用三十乘号,再加上三十八分工就是零点五乘三零八,哎,他们之间的差就是二八十八,减去七十几,所以这个一百四十九度就是指我们这个中面角。再比如这第二个例子, 十分针转动了十一分钟,所以是十一六乘以十一,也是六十六度。时针转动了七小时十一分钟,七小时就是七乘以三十,再加上十一分钟,就是零点一乘以零点五乘以十一。这时候我们看是时针转动的角度大,所以就用时针转动角度减去分针转动角度,最后结果是一百四十九点五度。最后一个例子, 分针转动五十三分钟,就是六乘以五十三。时针转动一小时五十三分钟,所以就是一乘以三十,加上零点五乘以五十三, 然后他们的差等于二百六十一点五,我发现二百六十一点五是大于一百八十度的,我们一般算的角度在初中范围内算的角度都是指小于一百八十度角,所以这一题的时针和分针的假角应该是指这个角,我们需要再用四百六十度减去二百六十一点五,哎,得到这个结果是九十八点五度。 通过这三个具体的弟子,我们可以试着总结一下一般的这个重面角该怎么算。首先我们要考虑到,如果这个 分针转动的夹角大于时针转动夹角时,最后的结果应该用分针的角度减去时针角度。如果是时针转动的角度大于分针转动角度时,最后的结果要用时针的角度减去分针的角度。当然我们可以通过一个绝对值把这两种情况合在一起。所以关于哎这个夹角的具体计算是可以当成是 时针的角度减去分针的角度,然后加一点绝对值,这样就只有一个结果,不管是谁大谁小都只有一个结果。那么具体的角度应该怎么算呢?比如如果这个时间是 mdn n 分钟,首先还是先看分针转动的假角啊,是走了 n 分钟,所以分针转的角度就是六乘以待 时针转动角度啊,是 m 小时 n 分钟, m 小时的话就是三十乘以 m, n 分钟的话就是零点五乘以二,最后合在一起就是三十 m 加上零点五分,然后再用刚才得到的一个结果,哎,他们的夹角是时针减分针的一个绝地值,带入跨减,最后得到一个结果就是三十 m 减去五点五 n 的绝地值。 不过最后我们还要考虑这个计算的夹角到底有没有超过一百八十度,如果他们的夹角没有超过一百八十度,哦,分针和时间的夹角就是这个三十二度减去五点位的值,如果他们的夹角,哦超过了一百八十度,我们算的这个结果是不能作为最终结果的。 我们算的角,初中算的角度是要保证在一百八十度之内的,所以可以再用三百六十度减去刚才的角就是最中一夹角。最后我们再对这个空式进行一个简单的总结, 第一步就算这个绝对吃,这个时针和分针转动夹角插的一个绝对吃,然后要比较这个结果和一百二十度大小,如果他小于有八,哎,最后就是这个结果, 如果他大于一百八,再用三百六十度减去这个事情。所以最终关于钟面角计算,我们只要记住这两个公式就可以了,不过公式总归会忘的,所以我们还是最好把整个思考过程,一个计算过程题解清楚。
95千尘(初中数学)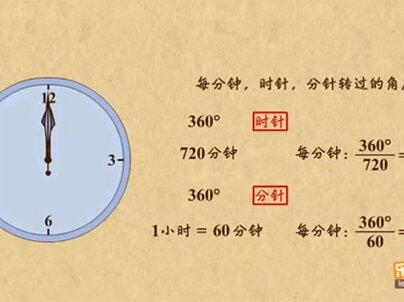 02:25查看AI文稿AI文稿
02:25查看AI文稿AI文稿时钟你很熟悉吧?那你知道每分钟时针和分针走过的角度是多少吗?先说时针,时针走一圈转过的角度是三百六十度,走一圈的时间是十二小时,也就是十二乘六十分钟,即为七百二十分钟。 七百二十分钟走了三百六十度,那每分钟就走了三百六,除以七百二,得零点五度。 说完时针,再来说分针,分针走一圈转过的角度是三百六十度,而走一圈的时间是一小时,即为六十分钟。六十分钟走了三百六十度,那每分钟就走了三百六,除以六十,得六度。 看来时针每分钟转零点五度,分针转六度。利用这个结论,咱来看个中面角度的问题。九点二 二十五分,你知道时针和分针的角度是多少吗?先把九点二十五挂出来,时针在九点往上一点,分针在五,这个位置要算的就是这个角度。 你看这一整圈是三百六十度,桌面上有十二个小格,那每个小格就是三十度,所以这四个角度都是三十度,加在一起就是一百二十度。现在只要算出这个小角度就行啦。 时针指在这时是九点,时针指到这时是九点二十五分,所以这个角度就是二十五分钟时针转过的度数。 刚才算过,每分钟时针转零点五度,那二十五分钟时针转过的度数就是二十五,乘以零点五,得十二点五度, 所以这个角度就是十二点五度。接着把这两个角度加起来,就是时针和分针的夹角啦,也就是一百三十二点五度。 以后再求时针和分针的假角,你就先数出有几个三十度,再利用时针每分钟转零点五度,去把这个小的角度求出来。 好了,总结一下这个视频我就给你讲了中面角问题,有个结论,你得记住,时针每分钟转零点五度,分针转六度。 另外在求中面夹角时,先数出有几个三十度,再利用时针每分钟转零点五度,求出这个小角的度数。怎么样,明白了吗?明白的话就速速去刷题吧!
4512大成老师教育圈 14:20查看AI文稿AI文稿
14:20查看AI文稿AI文稿我们看到今天这个题,今天这个题是大年初二那一天有一位同学问的,我们看一下 中面上的指针在九点的哪一时刻,时针和分针的位置与七的距离相等 啊,这种题型常有,还有一个口号是说时针和分针关于七对称啊,当然这个题距离相等,那就比对称多了一个情况了 啊,这是一个中面角问题。呃,我希望能够讲这个题目之前,我们能够把中面角的相关知识进行一下梳理,好吧, 哎,中面角问题,中面角的本质,它是一个锥级问题,一个环形锥级问题。我们知道锥 问题,它就一个核心的基本公式,那就是路程差等于速度差乘以追击时间。之所以说中面角问题,它是一个特殊的追击问题,那么它特殊特殊在哪里呢? 第一个,时针和分针它的速度是固定的。第二个,它的这个椎体是一个环形的,所以我们可以把时针和分针它们的这个路程,一周的路程,这个一周,这个环形长度啊,我们可以把它看作是三百六十度。 所以那么这里啊,我们说到了路程差和速度差,我们就来看一下 时针和分针他们的速度是一个什么关系,他们的速度是固定的啊,那么分针的速度是六度每, 时针的速度是零点五度每分,那这是怎么来的呢?其实我们知道分针走一圈,他是走了三百六十度,对吧? 那么他经历了多久呢?一圈是不是就是一小时,也就是六十分钟,所以三百六十路程除以时间就等于他的速度,所以他的速度就是六度每分, 这就是分针的速度,那么时针的速度呢?我们知道时针走一圈是三百六十度,那么他如果是除以十二个小时,对吧?那么这里他就会变成度尾时, 所以我要除以十二个小时,每个小时是六十分钟,那么这时候我算出来的单位也就是度每分路程除以时间三百六十,除以七八,所以他的速度是零点五度每分, 这就是分针和时针的一个速度计算。呃,然后我们还需要知道一点,那就是在那个钟表盘上一大格,它所代表的度数是总共三百六十度,被分成十二大格,所以每一大格是三十度,然后三十度 六倍分成五小格,所以每一格是六度啊。然后再就是我们还需要知道这一点,时针的速度是零点五度每分,分针的速度是六度每分,他们是十二倍的关系。 ok, 好,那么接下来我们再回到看这个公式,路程差不知道速度差,现在其实他们速度都是固定的,所以他们的速度差就是也是固定的,对吧?分针对十的,那所以是六度 减零点五度,那就是啊, 六减零点五,对吧?这就是他们的速度差,所以说他是特殊的追击问题。速度差是知道的, 有些题目我们也可以利用他们的啊,这个速度的一个比值,求出他们所走的角度的一个比啊。然后这个中面角问题通常考两类, 分成两大类啊,第一个是什么呢?我已知时刻去求夹角是多少? 已知时刻求夹角,比如说问你八点二十时针与分针的夹角是多少?给你一个时间。第二个就是已知夹角 求时刻或者求经过的时间,那么这个上面这一类等下我们推出一个一般公式,那么直接可以把这一类题全部秒杀掉。关键就是下面这一类, 下面这一类它就有多种考法。第一个比如说以告诉我们一个起始时刻,然后呃,让我们去求 他是什么时候最简单的啊?什么时候分针追上时针,他们再统一重合,求重合时针和分针。再比如说 九点多少分的时候,时针与分针会重合,像这样的,那这个是其实重合他的角度不就是零度吗?对吧?好。第二个那就是呃,在同一直线上, 他说时针和分针处于同一直线上,那么这时候我们就要注意了,他可以是重合,对吧?是在同一直线上,还可以是反向,他们成一百八十度角,也是处于同一直线上,对吧?好。第三种常见的考法就是时针与分针什么时候会垂直, 这个时候我们需要考虑两点。第一个就是分针在追上之前垂直,在分针追超过了时针之后垂直,所以有前后两种情况,我们需要考论啊, 要做做什么讨论,这个直线上也是一样好。还有另外一种就是给给特殊点,我们也是一样的做法啊。还有一个就是我们刚刚说的一个对称,关于哪一个点对,哪一个时刻,或者说哪一个时间点对称,他到了谁是谁的距离相等,对, 这样的, 哇,好, 这是椎体问题,中间上的椎体。我们另外一种,呃,就是考相遇的,那就是时针与分针互换位置,互换位置, 像这一种互换位置也就是一个套路,啥嘞?他们位置一互换,意味着时针和分针,他们的路程和就是两周,也就是七百二十度,七百二十度除以他们已知路程和和速度和求时间,那就是 路程和除以速度七八十度去除以六点五,就可以把这个基本上剪出来,好吧,所以这一个比较简单, 这一个关键是这中间我们需要跟警方讨论。那么现在来我们先把这个秒杀公式推出来啊, 求任意时刻量指针的假角计算公式,比如说 a 点 b 分的时候,那么几点几分啊?我们就用字母把它代替,那么 a 点 b 分的时候,我们首先知道,假如它是 a 点的时候,我们以这个时间点 a 点整点为出发点,那么这时候 分针是不是指向十二这里,对吧?那么时针就以上一定是,比如说是五点,它是不是指向整点这里, 对吧?所以他的夹角公式,那么他们之间的夹角我就看时针的就行了,对吧?所以这时候时针与 十二点这个之间的加上,那是多少呢?那就是三十 a, 对吧?因为一大格是三十度,走了 a 大格,所以他已经走了三十 a 了。好,那么接下来他走了 b 分钟 分钟,走了 b 分钟一分钟分,分针的速度是六,走了 b 分钟,那么所以分针他走的路程 是不是就是六乘以 b, 对吧?但是注意这时候时针有没有走,时针是不是也在继续走,那么时针的速度是零点五度每分,然后走了 b 分钟,所以零点五 b, 这个时候我们只要比较这一个和这一个,他们谁大谁小就可以,哎,把它一算出来,拿大的减小的就是这两个角之间的夹角啊, 这里全忘了擦了,好吧, 好,那这时候我们就三十 a 加上零点五 b 减去六 b, 对吧?而假设它减大,这时候我们把它化减一下,这边呢?三十 a 减去五点五 b, 对吧?好,那这个时候啊,你怎么确定三十 a 就一定会比五点五 b 大呢?对不对?所以他们两个可以,可以,他大,可以他大。那这个时候我们就引入一个新的东西, 初中的一个知识点叫做绝对值,啥意思呀?这里面就是大的减小的,如果差大,那就要用差去减去三十 a, 五点五 b, 那就如果是三十 a 大,那就三十 a 减五点五 b, 反正我用大 大的减小的加上这两根竖线,角是大的减小的,那所以我们这个假角公式就是三十 a 减去五点五 b 取绝对值,比如说 这个成绩和这个成绩,他们谁大就用大的减小的。好,接下来我们再回到来我们原来那个题目上啊, 中面上的指针在九点的哪一刻,时针和分针的位置与七的距离相等呢?哎,这时候九点多时针肯定是指上九点到十点之间,对吧?那假设指上这里,那么七 七这条线在这里,对吧?好,那么这时候时针和分针的位置,那假设我分针,我走 走到了,是不是分这里有这个角,所以我分成也要是这么多,对吧?假设分成这里这个角,这是角一,这是角二,我们需要的是角一等于角二,对不对?那么这时候我们先看角一可以怎么表示? 角一是不是可以看到九点整,这里是六十度,再加上十等等这一块,那我假设他走了 x 分钟, x 分钟,这个分针从这里走到这里,对吧?那所以他走的角度,这里就是六 x, 而时针走的角度就是零点五 x, 对吧?这一个角那就是 零点五 x, 所以那么角一我们就可以写作六十度加上零点五 x, 角二怎么表示呢?关键就是这个角怎么表示呢?哎,这时候我们可以 通过这个大角减去上面,它做成六 x, 这个角,那是不是就是角二?所以角二应该等于 这里七个三七二百一十度减去六 s, 这就是角二,然后根据他们这个距离相等,所以我们角一样的人角二,这时候我们就把方程列出来了,六十加上零点五 s 等于二百一十减六 s, 好吧,就让我们解这个方程,那就是六点五 x 等于 一百五十加十,那就是十三, x 等于五百,十三等于三百啊, 同时除以,对吧?三 x 等于三百,图案解说, x 等于把它改变为带分数的形式,那就是十三分之四十二,二十三又十三分之一啊,也就是说在九点二十三又十三分之一分钟的时候, 这个位置他们是相等的,对吧?但是我们这时候还要考虑到一种情况,他既然在左边可以和他说,那走到七的右边是不是还可以到他距离相等呢?对不对?所以这个时候我们还要考虑另外一种情况,那就七点这个时刻,我们继续把它放在这里, 假设他是九点多,九点多,这个时候时钟走到这里, 他时针与七的夹角是这一个,那么分针他要走到这边也和他的夹角也是这一个,也是这么大,那是不是意味着时针和分针这时候他们是重合的, ok, 他们处于同一直线上,那是不是就是说九点多少的时候,分针追上了时针,是不是这个意思?所以他们的假掌应该是零度吧, 对不对?那么这时候他们的路程差从九点这一刻算起,那就是,那我们看这个啊,是不是刚开始九点整的时候, 时针在这里,分针在这里,他们之间相差是二百七十度,对吧?那就是九乘以三十啊?二百七十,二百七十度,然后追上来了,那所以路程差除以他们的速度差, 他们的速度一个是六,一个是零点五,对吧?路程差除以速度差就等于追击时间,所以是二百七十除以五点五,呃,五点五, 二千七除以五十五,我们再画一下,那就是四五五,二五,五百五百四十除以十一,对吧?然后再画一下,那就是 四一百四十九又十一分之一,也就是说时针,呃,我们这个是在九点二, 二十三又十三分之一分钟,或者是九点四十九又十一分之一分钟的时候,时针和分针的位置与七的距离是相等的。
156二秒老师 06:33查看AI文稿AI文稿
06:33查看AI文稿AI文稿baby, 妈咪爱的 baby, 今天来看到什么题?今天咱们再来看一道中面角的实际计算问题啊,父母和孩子们一块听,看看这个题你能不能听得懂? 说问你从四点整到五点整,这一个小时之内啊,时针和分针什么时候夹角是九十度?哎,这种题咱们该怎么做? 给大家画一个图案啊?这是四点的时候,五点的时候是不是十针从四转到五,而这个分针是不是又转了一圈啊?那在这个动态的这个过程当中,大家来看啊, 时针是不是就转了这一小格呀?就转了这一点,但是分针快啊,分针转转转转转,然后转了一整圈,对不对?那这个题的核心是一个什么?这个题核心是不是跟我们之前讲过的一元 方程里边那个追击问题很像呀?是不是他快,他慢,他一开始离着他有一段距离是吧?有一段角度,然后最后追上,追上之后又赶超了,这是不是一段追击问题啊? 所以说大家想这个核实为九十度啊,是不是第一种情况,是不是他追追追追追还没追上的时候,哎,跟他差着一个九十度,后来追追追追上了,重合了之后,再把他拉出去啊,把这个时针拉出去,又拉出去九十度,是不是两种情况啊? 那两种情况咱们说跟追击问题有关,追击问题是不是有一个公式啊?哎,有个公式叫做速度差,乘以这个追击的时间,是不是等于这个路程差呀?也就是咱们追击的这个 距离啊?好,这个公式我给大家再解释一下啊。举个例子,比如我问你,咱们这个时候咱不说他俩差九十度,我问你,从四点钟开始,什么时候?也就是四点多少分的时候,这个分针能把这个时针追上,大概在这个位置 啊,给大家画一下啊,这比如追上的时候啊,这是时针,这是分针,他俩是不是重合了呀? 重合了。那大家看啊,这个分针一开始从十二这个地方追到追上这个时针的时候,他转了多少度?他是不是转了这么一个度数呀? 他转了这么一个度数,而时针呢?时针从这走走到这,他是不是转了这么一个度数呀?那他俩之间差多少?差,不就差的这一块吗?这一块不就是那个从 十二到四这四整段,这不就是一百二十度吗?他是不是差了一百二十度?那这是他们差出来的路程差,对吧?对吧?追击时间不知道,我们追击时间设一个 x, 对吧?那速度差是多少?关键是这个速度差不知道速度差,我们上节课讲过啊, 时针的速度,时针是不是一个小时转三十度啊?一个小时是六十分钟,所以说时针一分钟转多少?是不是 三十除以那个六十等于零点五度呀?这是不是他每分钟他走的度数呀?那分针呢?分针一小时转一整圈,转三百六十度,那才六十分钟,一分钟转多少?是不是转六度呀? 那同样是这一分钟下去,时针和分针同时走,那一分钟差下去,分针比时针差 差了多少度?快了多少度?是不是快了五点五度啊?那速度差是多少?是不是这五点五度呀?一分钟差出去的差了多少?差了 x 分钟,最后等于多少?等于追了多少?等于追了一百二十度,对吧?追上了吗?差了一百二十度,所以 x 是不是解出来了? 所以这个题大家会的话,那同样的道理,什么时候差九十度啊?那第一种情况是不是没追上啊?没追上的时候差了多少?差了九十度?来,咱们来看一下啊,第一种情况是不是大概,哎?时针,时针走到这,然后分针, 分针是不是走到这?这是不是差出去九十度呀?他俩没走的时候差了一百二十度。走了多少分钟?他俩现在差九十度啊。差九十度说明什么呀?说明是不是分针追了十针,追出去三十度呀?是不是追了三十度? 那怎么练速度之下?刚才我们求了啊,一分钟是不是差出五点五度去差多少分钟啊?不知道,我们说 x 啊, x 一吧。啊,因为两种情况吧, 等于多少?是不是等于一开始的一百二十度减去现在差这九十度,也就是我 x 一分钟的时候我追出去,我追了多少?我追了三十度出去,那 x 一等于五点五分之三十一,看除不尽嘛,除不尽。我说啊,除不尽咱们用分数表示啊,这种题 来,三百都除以五,是不是十一分之六十啊?翻呀,也就是五分多钟啊,不到六分钟的时候,五分来钟的时候,人家分针就追,时针追出去三十度啊,追,追三十度,那这是第一种情况啊,第二种情况呢?时针大概追到这,哎,分针追上了之后又 又拉出去九十度,对不对?分针走了多少?分针是不是走了这么一段?时针走了多少?是不是走了这么一段?那用这个角度剪这个角度,是不是差出去的那个路程差?差出去多少?是不是差这个角和这个角啊?这个角是不是九十度吗?这个角是不是一百二十度吗? 最差率多少?他追了多少?追了二百一十度啊,对吧?那第二种我们是 x 二,对吧?速度差还是五点五乘以谁乘以 x 二,对不对?等于多少?是不是等于一百二十度加上了九十度了呀? 他不光把一百二十度之前的这个路程差抹平了,同时他追上来之后又拉出去了九十度,是不是追了二百一十度呀?所以这个 x 二也能解出来啊?五点五分之二百一,那就是五十五分之两千一,对吧? 同时约五十一分之,这是多少?四百二,对吧?四百二,也就是说不到四十分钟啊,三十多分钟,不到四十分钟的时候,他就不仅把这个差抹平了,还又落出去了九十度。 所以这个题最后啊,什么时候啊?四点十一分之六十分时啊,还有一个四点十一分之四百二十分时, 所以这个题是不是类似的是追击问题啊?啊?追击问题,一定要把这个公式搞明白啊,每一分钟差出去这五点五度,这用他们的速度差乘以这个时间,最后就是他们的路程差。好吧,听明白了啊,给张老师点点关注,今天的课咱们就上到这下课喽。
1223战老师开课了 02:53
02:53
猜你喜欢
最新视频
- 2.8万语数同行











