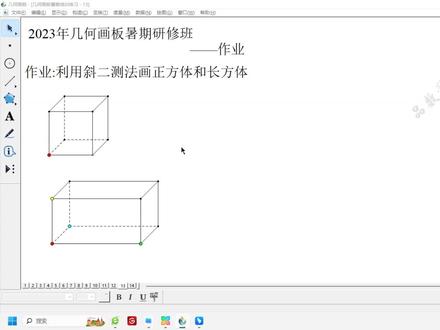
高二立体几何直观图斜二测画法

斜二侧画法在进入立体结合以后，我们往往会用一种斜二侧画法来画空间图形或者水平放置的平面图形的直观图。这种画法的规则我们通过一个水平放置的矩形来进行说明。 首先在这个原图中分别取 x 轴和 y 轴，他们两个互相垂直，原点是点 o。 画直观图的时候，我们保持 x 轴不变，把它记为 x 撇轴。 而外轴呢，倾斜四十五度，并且标记为外撇轴，圆点不变，于是就变成了一个所乘的角为四十五度的平面坐标系。然后在新的 这个坐标系中，平行关系保持不变。也就是说，原图中平行于 x 轴的，在新的图当中仍然平行于 x 撇轴。原图中平行于外轴的，那么在新图当中仍然平行于外撇轴。 比如说这条线段 a b 在原图中平行于 x 轴，那么跑到了直观图中， 就平行于 x 撇轴。 ad 这条线呢？原来平行外轴，那在新的图当中，他就平行于外撇轴，这是平行关系保持不变。 然后长度的规则是，原来平行于 x 轴的线段长度保持不变，所以说这个 a b 变到 a 撇 b 撇，这来了一 以后，他的长度仍然跟原来一样。但是原来平行于外轴的线段呢，到直观图当中，长度要变为原来的一半， 所以我们就取 ad 的一半。然后呢，让它平行于外片轴，画到这个直观图当中，于是这个 apd 片就变成了这样的一个线段。 同样的道理， d c 这条线段在原图中跟 x 轴平行，那么在新的直观图当中，也会跟 x 轴平行，并且以 d 撇为一个端点，它的长度与 d、 c 长度相等， 这样我们确定了它的四个顶点以后，再连接 b 片、 c 片，就得到了一个完整的直观图。 所以我们发现，本来一个矩形，用斜二侧画法画出直观图以后，变成了一个平行四边形，这样画也是为了突出立体感。所以如果要画一个图形的直观图，我们抓住这两点，平行关系不变。 原来平行于 x 轴与 y 轴的，现在还平行于 x 片轴与 y 片轴，只不过这个轴呢，它的夹角是四十五度， 原来平行 x 轴线段长度不变，平行外轴的线段长度变为原来的一半。那既然这样，我们发现对于一个平面图形，他画成直观图以后，他的底没有变，他的高应该在这条线段的基础上再 乘以三四十五度，这条线段是原来这个高的一半。所以假设原来的高度是一的话，现在这个长度是二分之一， 而这个长度呢，它是倾斜的，还不能代表现在这个图形的高，应该过地片向底边做垂线，而这个高呢，是四十五度所对的直角边，所以说他又是斜边的二分之根二倍， 二分之一再乘以二分之根二，就应该等于四分之根二。这样的话，它的底长度没有变，它的高变为了原来的四分之根二倍。于是像这样的平面图形，它的面积与直观图面积之间的关系 是 s， 原图乘以四分之根号二，等于 s 直管图。我们来看一个例子，这里给了一个直角三角形 o 撇、 a 撇、 b 撇， 说他是一个平面图形的直观图，也就是用斜二侧画法画完了以后的那个图，若 o 片、 b 片等于根号二，这是他的底边长。 问这个平面图形的面积，也就是原土的面积。我们刚才讲原土乘以四分之根号二，等于直观图的面积。 现在直观图是一个等腰直角三角形，那么它的底和高都是根号二，所以它的面积应该等于 二分之一，乘根号二，再乘根号二，也就是一，于是原图的面积乘以四分之根号二等于一，那么原图的面积就应该等于一， 再除以四分之根号二，等于二倍根二，所以选择 c 项。当然我们也可以通过把这个直观图进行还原，把它的外轴竖起来，保持 x 轴与外轴垂直， 然后利用我们刚才的规则去还原他的原图，再求面积，得到的结果是一样的。每天一个知识点，跟袁老师系统学习高中数学。

用十二色画法去画他的平面图形比较简单，如果画他的立体图形，比如说画这个长方体，对吧？ 啊？画出来的话他就相对而言比较复杂，但如果掌握好方法的话其实都不算难，我们去画他的空间几合体的时候，就包括他就涉及到了三维间隙，对吧？嗯，首先他呢就相当于是以这个呢取一个圆点吧， 我们把它标记为是 o 撇，然后呢在这里向右边这里的，我们把它叫做是 x 撇，对不对？ 嗯， x 撇走吗？还有一个呢是上面这个不叫 y 走，也不叫 y 撇走，他叫做 z 走，懂吗？嗯，然后 x 撇， o 撇 和 z 撇这个的度数呢？它是等于九十度的，对不对啊？还有一个呢，是 z 轴对不对？你可以稍微画的长一点，免得待会不够用啊，那 z 轴是多少的呢？ 这个是一撇吧，对不对？嗯，我们可以这样子记啊， 这个呢画的有点，这个度数有点太大了，对吧？我是目测的会有点不太准啊，你要知道。 好，那行，我们呢把它标记为是易撇这个角，这个度数呢，那个是撇， o 撇和易撇的度数呢？是一百三十五度，对不对？嗯，这是不是我们的第一步啊？我是总结一下嘛，第一步是间隙啊， 那第二步干嘛呢？ 第二步呢是做底面对不对？对，嗯，因为墙上是你铺，你要盖房子也是一样的吗？你要有根基啊， 对吧？你底面的话都不知道是什么东西，那怎么画呢？画不了对不对？你首先把这个底面先画出来，然后呢再什么高高楼啊，高楼叠起，哈哈，好，来看一下啥意思？底面，这个底面怎么做呢？ 我们首先要确定是哪些长度是不变的，对不对？在我们画这个空间几合体当中，他的 x 轴和日轴的长度是不变的，对不对啊？对，然 然后呢，他的什么是会改变他的 z？ 不是。哎，这里写错了，这里写重复了啊，这里应该是 y 撇吧，对不对啊？没问题吧，就这么想，没有啊，可能太晚了，对吧？有点困了。写到写到重复了啊，好，来看这里啊， 这个是不是三呢？嗯，宽是三，对吧？其实在这里当中就相当于是这里的话，我们要看他是以什么为中心， 对不对？嗯，你要看他是以什么为中心，以什么为中心的话，这个呢，你看你是怎么来去见就 ok 了，这个没有什么太大影响，懂吗？啊？嗯，就别说，我们就在这个 y 轴上，以他为中心去见，可以见不也是可以见的，懂吗？ 嗯嗯，你看一下什么意思啊？横过来就我们先确定这个点嘛，他的宽，对吧？就比如说这个呢，原来是三吧，嗯，就是 y 轴上嘛，是三嘛，对不对？ 那现在画的直观图的这个 y 撇到下面了，懂吗？啊？直观图的这个宽啊，会等于他原来这个宽的二分之一，那就二分之三吧， 嗯，对不对？所以说我们可以确定一下以哪个为一个单位长度呢？就比如说是，呃，以这么长为一个单位长度，好吧，这是二， 对吧？比如说这个是一，这个是二， 那么你这二分之三是一点五在这里吧，对不对？嗯啊，我把这一个点呢，把它标底面的话把它标记一下吧，就比如说是多少？ 嗯，因为它要是 abcd， 对不对？对，我可不可以把这个 a 撇 和这个 o 撇重合，可以不？嗯，这样子也可以的啊，你不要说不可，还是可以的啊，对不对？你看这个是 b 吧， b 撇，对不对？嗯，然后呢，你看一下我们在画的时候是不是应该说做什么？其实你在画的时候很简单，你把它这一段确定好了之后，后面都好画这个底面，对不对？嗯嗯，因为什么呢？因为它的长度和这个多少？ 和这个原来在平面直角坐标系当中他的长是一样，都是四厘米吧，对吧？那你把他标一下喽，你看一下这个是一吗？对不对？这是二，这是三，我这个是目测的啊，你可能有点不太准，对吧？ 嗯，来看，一二三四在这里。好，你看这是这么长，你用尺子把它量起来吗？也是这么长的来，对不对？ 能懂吗？嗯嗯，我是纯，纯粹是靠目测的。好，你看，你看，这样不是把他的底面给标出来了吗？ 对吧？好，其底面标出来之后，后面的那个好不好画？那第三步要做什么？第三步，我们总结第三 不错，垂心。那也不是说垂心就是么，做与多少与日轴平行的，多少 平行的线段啊。嗯，理解我的意思不？嗯，理解。对啊，就说说白了，你这个呢，刚才是做了底面，你后面是怎么样？是做高，相当于 把它给叠对，像盖房子一样嘛，把它给堆起来嘛，对不对？理解吗？ 懂我意思吧？懂，嗯，你看这个一轴应该是多少？ 这个一就是他的高吧？是啊，两厘米吧，这个会变吗？不变吧，不变。对，这个是不变的。那我们就好了啊，这个是一，对吧？啊，这个是二八。好，那定位定好了。这么长对吧我们目测一下哎这么长 这个目测有点难度哈哈。嗯 哎这个是啊。嗯看得出来吗如果是这样子的话 那我们这样子吧好吧。嗯喂听得见吗听得见。对其实这种这种是反作 做法有点不好搞对不对发现没有你看你这样子把它反做的话有点不习惯我一般都直接造土的这样子的话就搞了一点太官方了有点不适应了啊。 嗯好然后呢是不是把它给其他的都连起来了吧对不对。 嗯你看把这点了这其他线的话连起来那不就出来了吗是不是。嗯这感觉这么标准的吗都不像自己的眼睛原来这么会画图的吗对不对又是一个被为什么又是一个被数学耽误的美术老师对吧 哈哈哈 abcp 啊我我姐姐很很会画画啊他当时花了很多画画我当时拿张手抄报的时候我就用我姐画的 不是我发的每次把它挂上去的时候都有点虚心懂吗哈哈哈哈因为一挂就是一挂一个学期到下学期的时候还是在挂 嗯还是挂了新的又是我的我是一一挂都是挂好多副的啊因为我姐很会画吗我姐的是我姐的很高产的啊她一天可以画好几幅画啊啊 我怕他发霉吗我就拿去把他放到那个拿到学校去画那个黑板包去了啊因为我觉得我画的很丑啊所以我就不不用我的我一般是用我姐的作品啊哈哈哈哈哈哈对吧 啊如果真这么会画的话我就去做美术老师算了啊来看一下 abcd 啊你看标准吗？嗯，还 看的过去吗？啊？在这第三步嘛，对不对？你看做这个线之后呢？后面怎么办？后面的话说白了就是怎么样，就是他其余个边怎么样 变形圆起来，其余个边相连就 ok 了。嗯，对吧，没那么复杂。 嗯呃，再补充一点，就是其实我们在做图的时候，我们要，我们要这样子画吗？我们其实我们习惯上画长方体或正方体，是一般都这样子来，对吧？啊？怎么样？来一个方框对不对？ 嗯，就是把它给拼起来了。这是我们常规的操作方法吗？就是怎么样，然后这样子，对吧？哎，成了， 哈哈，对吧？一般是这样子做的。但是如果我们要刷的时候呢，你就要把它怎么样，就要精细化一点了，对不对？画的话不要画错，一定要把它的长宽高他们对，好来，可以吧？嗯嗯，好，那行。

一个题目带你学会第二次画法。好，我们来看这个题目，一个边长为傲的正方形，想画出他的直观图， 那么我们第一步先建立合适的平面之交坐标系。这个合适的意思是让尽可能多的边在坐标系上，或者尽可能多的顶点在坐标系上 活着，是为了下一步的方便。选择这个整多边形的中心为圆点都是可以的，都是合适的。根据经验慢慢的选择好正方形，我们选择的是一点点 a 位圆点，建立入图的平面之交坐标系。 那么第二步呢，在右边建立一个这样的坐标系，就是 x p o 轴和 y p o 轴的加 夹角是四十五度，这就是斜耳侧的斜的来临，那就是两个坐标轴的夹角变成四十五度。精彩的一步来了，我们来看啊，在 x 撇轴上截取这个 o 撇， b 撇等于 o b， 就是说平行于 x 轴的线段长度不变，那么得到了比撇点，然后在外撇轴上截取线段 o 撇，底撇等于二分之一的 o 底， 平行于外轴的线段长度减半，这就是邪恶色画法的本质。现在我们已得到了正方形三个顶点对应的作品位置下面就剩下点 c， 那点 c 的位置呀，已经确定了，那方法很多，比如说我们 可以过底撇做 x 撇轴的平行线，过 b 撇做外撇轴的平行线，两个平行线必然相交，或者呢，过底撇做 x 撇轴的平行线，然后在平行线上截取低撇，细撇等于 o b， 就是平行于 x 轴的线段长度不变。或者呢，过笔撇做外撇轴的平行线，然后截取 b 撇， c 撇等于 o 撇，地撇等于原来的二分之一的 od， 也就是说，平行于歪轴的线段仍然平行于歪轴，但是长度减半，这就是邪恶策划法的本质。然后呢，擦去多余的线段，就得到了我们想要的正方形的直观图，你看 明白了吗？接下来我们看再稍微复杂一点的等边三角形的直观图的画法。 我是哲树，一个有自己教育理念的公行者，让每一个有志于学习的同学都能得到最好的教育。关注我，一起走！

这个视频我来讲讲如何用斜二侧画法来画直观图。比如要画这个六边形的直观图，方法分四步，第一步，画坐标系，先在六边形上建个直角坐标系，然后 x 轴不变，外轴倾斜四十五度，分别写成 x 一撇轴和外一撇轴，这就是斜二侧画法的坐标系了。 画好了坐标器。第二步，画坐标轴上的点，规则是 x 轴上的长度不变， y 轴上的长度减半，简称横不变，竖减半。现在来看， x 轴上是 a 和 d 对应，画到 x 一撇轴上，根据横不变， a 对应之二是 a 一撇， d 对应之二是 d 一撇。 再看外轴上是 h 和 g， 根据数减半， oh 减一半，这二是 h 一撇，显然这就是 g 一撇。搞定。接着第三步，画平行坐标折的线，规则是平行关系不改变，并且还是 横不变竖减半，看 ef 平行 x 轴划过去还是平行 x 轴根据横不变，所以长度是一样的。再看 bc 也平行 x 轴划过去也不变，平行线就搞定了。最后就是连点，把这些点连起来，就得到正六边形的直观图了。 图画好了，咱来总结下写二侧画法。方法主要分着四步，从坐标器到坐标轴上的点，再到平行坐标轴的线，其中的规则一定要记好，横不变，竖解半，平行关系不改变。 刚才是给你平面图，让你画直观图，如果给你这个直观图，你能画出他的平面图吗？步骤跟刚才一样，第一步还是画坐标系，第二步还是画坐标折上的点，根据很不便，显然这是 a， 还有这二是 c， 这样坐标折的点就搞定了。接着第三步，画平行坐标折的线，他 平行外轴对应 ab， 就是平行外一撇轴的。要注意， a 一撇 bb 长度是减半以后的，所以 ab 的长度是他的两倍，这样 ab 就画好了，最后连接 bc， 就得到三角形的平面图了。 像这样给你直观图，要你画平面图，步骤是一样的，原来长度不变的还是不变，但是原来长度减半的就别忘了乘二 图。你已经绘画了。如果我进一步问你，这两个图形的面积有啥关系，你能找出来吗？比较一下这两个三角形，先看底，分别是 ac 和 a 一撇， c 一撇，显然是相等的。 再看高，这个是 b 撇第一撇，这个是 ab， 有啥关系呢？想一想， a 撇 b 撇等于二分之一， ab， 这是四十五度角，那 b 一撇第一撇就等于这一段乘上二分之根号二，所以 b 一撇第一撇等于四分之根号二。 ab 底相等高是他的四分之根号二，那直观图的面积就等于平面图的四分之根号二。你可以记住这个结论，他不仅在三角形里成立，由于任意多边形都能分成三角形，所以也都成立 好了。回顾刚才的内容，关键掌握两点，首先是十二侧画法的规则，横步变竖减半，平行关系不改变。其次，直观图面积等于平面图的乘四分之根号二。怎么样，你学会了吗？如果学会了，就速速去刷题吧！

四个观察长方体的盒子，可以看出每个面都是平的，给我们以平面的形象。 生活中像这样的也给我们以平面形象的例子非常多，例如我们周围的墙面、地面，还有平静的水面等等。在数学中，我们研究的平面是平的，也是无边无言的， 我们在日常生活中所遇到的平面大多数是长方形，所以我们会用长方形来表示平面。 另外根据长方体物体在地面上的投影，或者说我们观察的角度，我们也可以发现， 一般我们看到的是呈平行四边形的形状，所以我们也可以画一个平行四边形来表示一个平面。 一般的我们会把水平放置的平面画成一边是水平位置，另一边与水平线的夹角为四十五度，这样一个平行四边形。那么问题来了， 观察长方体模型，我们能够看到这个长方体模型的几个面呢？ 我们教材中有这个讲台上的粉笔盒的图片，它的观察视角和左侧的这幅图形的观察视角有什么不一样 呢？他又能观察到这个盒子的几个面呢？啊，我们可以发现左侧的这个长方体的模型，我们的观察的角度是在右上方的位置， 右侧粉笔盒的观察角度我们选取的是左上方的观察角度。好，那如何将左侧的这个长方体模型能够很直观的画在纸上呢？ 根据我们的生活经验，大家可能都想到了，我们可以先把它的底部用平行四边形 a、 b、 c、 d 来表示， 然后根据长方体每个面都是长方形，做出底面的垂线，使它们的长度都等于长方体的高， 然后将这些点顺次连接，这样我们就画好了一个长方体的盒子。 大家的这些经验都是非常好的，不过在这里我们左右对照一下，我们可以发现， 在我们观察中应该有三条棱是被遮挡住的，那我们数学上画图的时候，被遮挡住的棱我们用虚线表示。 这个画图的过程有点像我们生活中的造房子，确定底面的平行四边形就相当于是打地基， 做这个平行四边形的高的时候，就相当于是我们照墙面，而将上部的四个点 景点顺次连接，也就像给房子照上房顶。那这样的一个生活经验在我们的数学中也是可以印证的。 这些画法可能还会有各式各样的，不过今天这节课我们要一起学习的是长方体的斜二侧画法。字图中最常用的一种画直观图的方式，也是要求同学们掌握的一种画法。 那么斜二侧画法是如何画一个长方体的呢？接下来我们就一起来学习一下长方体的斜二侧画法。步骤一， 画平行四边形 a、 b、 c、 d， 使 a、 b 的长度等于长方体的长， a、 d 和 b、 c 的长度等于长方体宽的二分之一角 d、 a、 b 等于四十五度。同学们可能会有点困惑， a、 d 的长度为什么要等于长方体宽的二分之一呢？ 其实啊，这是我们长方体写二册画法的一种规定，它的目的是为了使我们画的直观图能更加逼真，也为我们将来的学习打下基础。 步骤二，过 a、 b 分别化 a、 b 的垂线 a、 e 和 b、 f 过 c、 d 分别化 c、 d 的垂线， c 级和 d、 h， 使它们的长度 都等于长方体的高。 步骤三，顺次连接点 e、 f、 g、 h。 步骤四，将被遮住的线段改用虚线，也就是隐藏线来表示，这样就完成了长方体的直观图。 好，我们来梳理和归纳一下， 在上述的画法中，大家是否觉得有一些地方是我们画图的难点，让我们再来回顾一下。 对于一个实际的底面为 a、 b、 c、 d 的 长方形平面，我们画图的底面是平行四边形 a、 b、 c、 d。 这个画图的过程中，我们要注意原本的长方形的夹角九十度，要画成平行四边形中的四十五度夹角。 长方体的底面 a、 b 的长度和我们平行四边形水平线方向的 a、 b 的长度是相等的。 特别要注意的是，对于长方体的宽 b、 c 八厘米，在画图的过程中，根据我们的斜二侧画法的规定，要取 它的一半，所以 a、 d 和 b、 c 的长度为四厘， 这些地方都会影响我们画图的准确性，所以我们大家画图的时候要严格的按照规定，借助画图工具 非常仔细的完成每一个步骤。这里老师呈现了我们刚才看到的一个正方体，正方体的长和宽以及高是相等的，我们可以看到正是因为我们使用了斜二侧画法， 我们这个正方体看起来就非常的逼真。好，那么我们画图中，通过我们生活中模型的对比， 我们看到有被遮挡的三条棱，要将它转化成虚线的形式，这一方面是我们的画图习惯和规定，另外一方面他能够很好的实现了虚实的衬托， 所以大家在画图的过程中也要遵循这个规律，看得见的人画成实线，看不见的人一定要画成虚线。

我们来看这个题目，是告诉了直观图是正方形求原图的周长，我们需要把正方形还原成原来的图形。 我们知道直观图是把坐标系改为加角，是四十五度得到的。要想还原回去，那么先要找到这个 直观图的坐标系，可以根据图形的特征来选择合适的，和原来一样，让尽可能多的点在坐标轴上。我们观察到正方形，他的对焦线平分了内角，所以呢，这个角就是四十五度，建立如图所示的这个心二侧坐标系。 这样一来的话，坐标轴上就有三个点了。根据之二至关图及二次画法的原则，我们回复过来，画出 原图的平面纸叫坐标细移。平行于 x、 p 二轴的，在 x 轴上长度不变，截取 a、 b 等于 a 撇 b、 p 平行于歪撇轴的仍然平行于歪轴，长度是原来的二倍，那所以 a、 c 要等于二倍的根号二。 然后我们得到了三个顶点的对应点， a、 b、 c 需要得到点地，那需要得到点地，只能依托于平行于 x 轴或者平行于外轴，也就是平行于 x 撇轴外撇轴的线段。 那我们就选择 d 撇 c 撇，它平行于 x 撇轴，那么我们就过 c 做 x 轴的平行线。在平行线上截取 c， d 等于 c 撇 d 撇，因为它平行 爱喝的粥呀，长度不变，所以说呢，接取 cd 好得到点 d。 于是呢，我们连接 ad 就得到了正方形的原图。 那原图呢，是个什么形状？我们一观察，发现原来是一个平行四边形呀。要想调到的周长，我们缺少，缺少了哪条边呢？缺少了 bc， 找到 bc 所在的三角形 b、 a、 c， 因为它是直角压那，所以勾固定离可以得到斜边笔写等于三，所以原图的周长就等于八， 你看明白了吗？原来直观图要想回复成原图，要找到家教是四十五度的那一个条件，这样就能顺利的回复过来。于同学说，如果遇见了不好回复的情况下该怎么办呢？我们再来举一个例子来说明，没有 四十五度的时候该怎么办？ 我是哲树，一个有自己教育理念的公行者，让每一个有志于学习的同学都能得到最好的教育。关注我，一起走！

好，这五边形的直观图呀，是比较复杂的，我们来看，先建立合适的平面直角坐标系， 我们选的是正无边形的中心为圆点，然后呢， e， 他的对称轴 a， f 为完轴，那 x 轴不用说了，肯定是过圆点，垂直于完轴的这一个直线为 x 轴建立平面之交坐标系。 然后我们来看一看有哪些点在坐标轴上。哦，我们看到了 a 点在那，所以呢，直接在在新的坐标系第二侧坐标系上， op a， p 等于二分之一的 o a， 得到了点 a 的对应点，然后呢，借助于 f， 就是截取 op f， p 等于二分 之一的 of 也得到了 f 的对应点。下面我们来找 cd 还是找 be 呢？那先处理 be 吧， be 这两个点他不在坐标轴上，然后经过他的线段也不平行， x 轴也不平行，歪轴，怎么办呢？ 我们上一个题目有经验，那就是过 b 和 e 向 x 轴做垂线啊，我们做了垂线，得到两个垂足及 a 七， 然后我们在对应的 x 撇轴上找到对应的线段， o 撇， g 撇等于 o g， o 撇， h 撇等于 o h， 然后定住了他们两个的位置，在过 gp 做外撇轴的平行线，过 acp 做外撇轴的平行线，在平行线的截取 b 撇， g 撇等于二分之一的笔记，一撇 a 系撇等于二分之一的 eh， 这样一来我们就得到了对应点， b 撇和一撇。 好，剩下 cd 和我们前面的是一样的，只需要过 fpa 点做 xpa 轴的平行线， 然后在这个平行线上截取 f p， c 等于 f c， f p d 等于 f d。 总之下册一句话，那就是平行于 x 轴的还平行于 x 撇轴长度不变，平行于外轴的，那就平行于外撇轴，长度减半。 如果既不在 s 轴上，也不在歪轴上的，通过做支架，支架就是向 s 轴或者向歪轴做垂线，找到他 对应的那个点，这样啊，就可以搭桥做出任意一个多边形的直观图，你学会了吗？下面我们来看一看有关的计算题。 我是哲树，一个有自己教育理念的公行者，让每一个有志于学习的同学都能得到最好的教育。关注我，一起走。

这个题目 gay 的是直观图，说直观图是矩形，要想得到原图，我们要找到夹角四十五度的那个元素。可是呢，这个矩形的长是六，宽是二， 不太好找，那我们就做一个四十五度吧，以 o 撇为圆点，然后做一个角，是四十五度。好， 那他的外撇轴就交 c 撇、 d 撇与底撇。我们现在这个角呀，是四十五度，我们就可以得到旁边的这个三角形， o 撇， c 撇 d 撇，这个是等腰直角三角形，所以呢，就得到了 c 撇、 d 撇的长。 好。现在呢，啊，我们可以求出 o 撇底撇哦，他的长是二倍跟二，为什么要求出他呢？因为我们斜二侧的原则是，平行于 f 轴的还平行于 x 轴，平行于 y 轴的还平行于 y 撇轴。所以呢，我们一定要找到 y 撇轴上的位置啊，建立平面指标坐标系，在 x 轴上截取 o a 等于 o 撇， a 撇长度不变，然后在 y 轴上截取 o、 d 等于二倍的欧撇底撇。所以我们刚才需要计算出欧撇底撇，如果刚才没有计算的话，现在计算出来是一样的，等于四倍跟二。好，我们得到了点地， 那再来观察剩下 c 撇和 b 撇。我们说，要想得到原图，必须找到过 c 撇、 b 撇与原图的 x 轴或者是 y 轴平行的线段，平行的，那只能是 c 撇和 b 撇。这里 c 撇、 o 撇是不起作用的，这是他画图的原则。那 c 撇、 b 撇与 x、 b、 a 轴平行，我们就过 d 撇做 x 轴的平行线，然后在上面截取 d、 c 等于 d 撇 c 撇，嗯，不变，长度不变，截取 d、 b 等于 d 撇、 b 撇。 这样一来的话，我们就得到了四个顶点的对应点，然后把多剩下的这个线段连接起来，就得到了原图。 我们观察一下，原图好像是一个平行四边形，一条边 o a 当然含等于六，另一条边 o， c 和 a、 b 呢， 当然是放到三角形中来解决了。找到 o c 所在的三角形 o， c， d， 这个三角形呢，是直角三角形，我们知道 c d 等于二，然后呢， o d 等于 四倍根号二勾固定里等于根号下四，加上三十二根号三十六等于六。哦，原来 oc 也等于六呀，那所以这个平行四边形就是菱形，所以呢，它的周长就是二十四。 原来一个置换图要想恢复成原图，那就是找到夹角是四十五度的条件，如果实在没有的话，那就勾造一个四十五度的角。 构造了之后呢，就可以得到坐标轴上的点，然后再找到与 x 轴、 y 轴平行的线段，找出它们对应的点的坐位置，就可以得到原土的大小。你学会了吗？ 我是哲树，一个有自己教育理念的躬行者，让每一个有志于学习的同学都能得到最好的教育。关注我，一起走！