GaussDB不支持rlike函数
粉丝602获赞3.4万
相关视频
 02:53
02:53 05:53查看AI文稿AI文稿
05:53查看AI文稿AI文稿我们知道分段函数在每一段上的解析式都是不同的,那么这类函数的单调性如何判断?又该怎样利用他的单调性来解题呢?也就是我们今天的一个主题。那么我们先来看这里的第十六题,也是我们刚才说的第一个问题如何判断分段函数的一个单调性。 如此,题目给出了我们一个 f x, 它写成了小于等于一和大于一的两段。然后呢,这个题目需要我们解决它在 r 上是单调递减函数的这样一个问题,然后最后需要求解里面的一个参数的范围。那么在讲这个题之前呢,我们可以先回一个问题啊,在初中阶段, 我们如何去说 f x 等于 x 分之一,也就是反比例函数的一个单调性?我们有没有说他在定义里面是单调递减的?我们应该是没有说这个话的对吧?那么高中阶段,我们会去讲他是在负无穷到零,然后呢,逗号零到正无穷上是单调递减的。在初中阶段, 你会讲它在第一项线和第三项线里面是单调递减的,对吧?那所以它为什么会和其他函数单调性的描述不一样?就是因为它是一个分开段的函数,它在 x 等于零这个地方需要去做一次分段。那么如图也是一样的,我们把这个分段函数单调性画个图去做个示范。假设我们随便去画一个分段函数, 那么在 x 等于零的这个地方,我们进行分段。就比如说,如果我画成了这样的一种状态,前者我们点一个空心点,后面点一个实心点,分别来表示端点可取或者不可取。那么这个函数符合我们对于单调递减函数的概念吗? 应该是不符合的对吧?单调地点函数,顾名思义,我们可以认为这个函数左侧的点一定是要比右侧的点要更高才可以对吧?那么这个点在我分段的这一节处应该是没有办法满足这个要求的。那所以什么样的函数才能做到真正 分段函数在定义域内单调递减?我们可以再画以下的两个例子。首先简单一点的,比如说我这两个函数虽然是分段,但是在这个地方接头了可以吗?那么这个应该是可行的对吧? 左侧的点的确都比右侧的点要更高。那么另外一种是什么样的呢?他的确断开了,但是断开的时候 左侧的这一段会比右侧的这一段要怎么样呢?要更高一些。那是不是也能做到左侧的点都比右侧点要高? 那所以这个就是我们对于分段函数单调性的一个理解与应用。那下面我们再回到这个十六题,我们来看。那首先想在二上都是单调替减函数,那么两段都应该是递减函数对吧?那么第一行的二次函数说他的对称轴的控制,他的对称轴 应该是等于负 a 的对吧?那所以负 a 和一是什么样的关系,我们需要去想一下。那么第二段是一个依次函 函数,那么一次函数它的单调性是由前面的一次项系数 a 去控制的,那所以 a 的正或者负你要有一个理解对吧?那最后我们再来看,那么仅仅满足两个分段都是单调递减,还够用吗?按照前面我们给出的示意图,应该是不够用的。 比如说我们的示意图第一个就应该是一个错误的选项对吧?那所以为了保证他真的在 r 上单调递减,那需要满足怎么样?需要满足后面这两种图像,也就是前一段的这个值,这个端点的值比后一段的端点值要怎么样呢?要更 高一些,对半。那所以将 x 等于分别代入第一行和代入第二行,那么第一行的 x 平方加二, x 加三,在 x 等于一时要大于等于后者的 iax 加一,在 x 等于一时候的一个值。这就是我们对于十六题的一个阐述。两个分段分别需要单调递减, 在街头的端点处有需要产生什么样的要求?看这里的图像会比较清晰一点。那么这个是我们刚才说的第一点。如何判断分段函数单调性?那么第二点就是什么呢?如何利用分段函数单调性?也就来看我们的第十七题。已知函数 fx 写成了两端的形式,两个函数的分段的点在 x 等于零处。 然后后面又给我们 f m 小于 f 二减 m 的平方,然后问我实数 m 的取值范围。对于这样的题型,我们首先要有个概念,有没有可能 将 m 和二 gm 的平方带入函数表达式去求解?那么这件事情要去想,应该是不太可行的。为什么?如果你要去做代入的话,那么你要需要去做分裂讨论的。 比如说 fm 我想带入这个表达式,那你就要去想 m 到底是比零大还是比零小,需要做一次分类讨论,同样的二减 m 的平方是大于等于零还是小于零?又需要再做一次分类讨 讨论,将这些分类讨论和为啊统一的体系之后才能去做这个题目对吧?那所以这个题目就被我们做的超级复杂了对吧?那有没有些简单的方法呢?或者说这个题目到底应该怎么做?我们来看一看这里的第十七题。 那么分段函数,那我们先把它的图像是能画的对吧?对于高一阶段而言,树形结合应该是一个很重要的技能,也是必须要去掌握的技能。 首先,这个函数大于等于零的部分是一个开口向上的二次函数,它的对称轴应该是在负二分之一处。然后呢,当 x 等于零的时候呢?这个函数值应该是等于一。所以结合以上的几点,我们的图像应该是什么呢?你只会保留一个往上递增的 二次函数的一部分对吧?像图所示,完整的应该在左侧还会有些虚线区域对吧?虚线表明他实际取不到,那我们就不去画这个部分了。然后另外一侧二 x 加一,应该是一个单调递增的一个一次 函数的形式对吧?那我们就来画它,那画出来的结果应该是一次函数,大家就比较熟悉了,画出来就是这个样子对吧?那所以这个图像在结合前面我们在十六题里面提到的分段函数单调性的一个概念,你能感觉出来这个函数应该是在定义域内都满足单调递增的对吧? 那既然是个定义域内的单调递增的函数, f m 想要小于 f r g m 的平方,那其实我们也直接利用穿脱法比较里面的变量的这个范围就可以了对吧?你的 m 比 r g m 的平方更小就可以了。 所以这就是这么的两个题。那么这两个题总共就是为了什么?为了让我们去感觉出来分段函数单调性和普通函数单调性的区别大于在于什么地方? 主要就是什么呢?主要就是你要记住这里我们画出了三个图像,那么这里是单调递减的图像对吧?你能类比的画出单调递增的图像吗? ok。
 09:21查看AI文稿AI文稿
09:21查看AI文稿AI文稿e s 六之前咱们写程序呢,都是用回调来解决这个异步的,但是呢,出了普洱密斯之后,哎,这个解决问题就方便很多了。怎么解决?咱们看一下什么是普罗密斯对象?普罗密斯对象是 es 六提供的一个对象,那我们想创建普罗密斯对象,可以用尿关键字,你有普罗密斯括号啊,那我就可以这样啊,这样, 比如说 like 啊, p pluns 等于 nupromes, 大家看到了吧?这,这个很简单啊,创建对象,比如用六国研制了这个,这个没什么说的啊,那这个 p 的话,他是有一个方法的,叫正正, 这个证有什么用呢?通过这个证我可以拿到一部数据,我这里写一下,重要的就写下通过证拿到一部数据。那大家一听那个,哎呦,我拿到一部数据,刚才咱不是讲了吗?拿一部数据不是通过回调函数吗?通过回调函数吗?啊,对的, es 五,咱们用 毁掉函数,拿一部数据。 es 六呢,我们可以通过这个任拿一部数据,这样的话更方便维护,不会出现这个,这个这个毁掉地域啊,那怎么拿呢?咱们来看一下 supermes, 他有一个括号啊, 括号里面我们应该加一个函数,而函数里面有一个参数,叫瑞兽,瑞兽啊,这个瑞兽是什么意思呢啊?他可以把一部的数据传出来,瑞兽 可以,可以将一部数据传递出来,吕兽可以把一部数据传递出来,怎么传呢?我可以这样,吕兽括号,然后这里出个 哈喽 word, 大家看啊,那我传出来外面怎么获取?刚才咱们说了用顿获取,对吧?批点顿,然后顿的参数也是一个函数,翻个身, 你也可以写箭头函数啊,都可以啊,可以从这落个低塔。那这个低塔是什么?他就是瑞兽传出来的这个数据,所以批点正拿到的这个低塔就是 helloword, 咱们看一下是不是刷新 helloword。 这个懂了之后咱们来解决刚才的问题。我把这个注视掉了。啊, 咱们刚才遇到了一个什么问题呢?一个奶茶,一个火锅,我现在需要按顺序拿到,先拿火锅,再拿奶茶,但是咱们刚才写的是用毁掉函数拿的。毁掉函数的问题是什么呢?啊?不容易维护,毁掉地狱,对吧?好,那我现在通过普拉米斯 来改造这个函数。首先 get, 咱们看啊,我 get t, 我可以给他做一个返回值啊,我不返回奶茶,我返回奶茶拿不到,对吧?返回奶茶拿不到,那我返回什么?我返回一个普奥米斯对象。普奥米斯对象,那这个业务逻辑我写到 普奥密斯对象里面,大家看一下,写到这个普奥密斯对象里面,把这个 f n 没有了,盖子 t f n 去掉, f 没有了啊,那刚才咱们说了,尼欧普奥密斯里面这个函数有一个叫瑞兽的一个, 呃,一个参数,这个蕊兽,我们调用这个蕊兽可以把数据传出来。奶茶的函数我就 改好了,就改造好了,改造好之后咱们咱先不改这个火锅啊,等会再一起改啊。改造好之后,那我现在调这个盖子替啊,咱的目的是拿奶茶,对吧?目的一定要清楚啊,目的是拿奶茶盖子替。括号,他的返回值是什么? 是不是这个普奥米斯对象?我不是蕊称一个牛普奥米是什么,对吧?伟称一个牛普奥米斯,所以说盖的 t 的值就是普奥米斯对象,那刚才刚才咱们写这个例子的时候咱看啊,这个例子啊,我牛普奥米斯 复制给了一个 p, 那我是不是可以用 p 调用这个正,对吧?啊?也就是说普洱没事可以用,可以用正,那我们再回来啊,刚才的这个 get 奶茶奶茶我是不是也可以认呢?因为盖的 t 是一个普洱的对象,普洱没事就可以用正,而且通过正可以拿到蕊兽传出来的值,我 句话听懂了吧?然后正,我怎么会一道数据呢?这个就直接一个函数了,对吧?刚才咱说了,正里面写函数,别写尖头函数,写普通函,普通函数 现场是不是也一样啊?然后这里有个雷塔,那我现在啃手点烙个这个雷塔,那这个雷塔是不是刚才咱说的这个 get 拿到的这个奶茶呀?那我们看一下现在的效果,刷新 一秒钟之后输出奶茶功能实现,这样写有什么好处啊?咱们接着说,就是这个好处啊, get 可以拿到一个奶茶,那咱刚才遇到的是什么问题,还记得吗?刚才碰到的问题是不是说通过回答函数获取数据数顺序固定的 时候呢?咱们需要一层一层签套会出现回掉地狱,那我用,我用这个普洱米会不会出现回掉地狱呢?不会了啊,好,那我们接下来把这个获取火锅的这个函数也给他改造成普洱米斯对象啊。那,那按照刚才的时候,首先把这个 f n 去掉啊,然后我直接蕊称一个普洱米斯, 然后把这个里面写是一个函数,然后这里有一个 resou, 然后业务逻辑是这个获取火锅,那通过 resow 把这个火锅传出来, 哎,火锅的这个函数咱写完了,那咱们刚才说了,我想先吃火锅,再喝奶茶。好,那咱现在写了,我要先吃火锅,那就 来出示一下在喝奶茶哈,那首先我吃火锅肯定是调用啊盖子号的 pose 对吧?括号,然后这是一个普通的对象,然后写真啊,那我要拿到这个火锅的数据,然后我输出这个逮他,肯输点,捞个逮他, 大家看现在能不能输出火锅。刷新 a, 然后你犯的二十一行,然后你犯的意思,然后他普洱米斯,你用普奥米斯啊, 牛,普拉米斯,我上面写牛了吧。写牛了啊,这没写牛啊,牛,普拉米是创建一个普拉米对象。 ok, 那继续啊。呃,先吃火锅,再喝奶茶,然后盖他点耗子泡点炖,然后刷新,一秒钟之后,啊,可以看到火锅,两秒钟之后可以看到火锅啊, 那你就说火锅拿到了啊,那第一个凳,大家看啊,这块就是普洱密室的用法了,第一个凳里面我们可以写一个蕊券, 趁什么呢?蕊,趁一个我接下来还想钓的普奥米斯对象,那么接下来想喝奶茶,对吧? get 括号 gett, 是不是一个普奥米对象?那刚才说了是,对吧,盖特替是普奥米对象,这样的话我就可以再连着震了,连着震,再震,然后翻个身对他括号, 然后 ctrl alt 对他,这样的话,我第二个正,就是调的第一个正的返回值,这个 pome s 啊,然后我们看一下效果 刷新,首先拿到火锅,然后再拿到奶茶,就是通过普洱米式的写法来实现一个获取异步的操作啊,链式的?对啊,一个链式操作。那大家看这个,如果说,如果说,我再接着我再接着我,我这个,呃。做做个 洗个澡唱个歌啊,保个养,做个什么?什么东西?大家看这个代码虽然还是还是不是特别友好啊,但是大家看啊,这个代码肯定是比刚才的回调函数要强很多,对吧? 这就是普罗密斯,可以解决异部问题,可以让异部的程序比那个回掉地狱更加好维护,这是普罗密斯的作用。还有其他解决方 吗?有啊,还有其他解决方法,就比如说你看这个不爽,对吧?还是一堆正,虽然比刚才的毁掉地域好了,但是这一堆正我看的也不爽,怎么办?接下来讲啊,性格函数。什么是我性格函数呢?就是说在函数前面加一个信可就是我性格函数了啊,但是当然这句话是 废话是吧?没什么价值,比如说我这个性格函数加 ait a 获取数据,然后,呃,性格函数的重点是什么呢?就是这个函数里面可以写一个哦喂他,哦喂,他可以加一个 promx 对象。好 好,那我说到这咱就直接写了,这个就不难了这就不难了,大家看啊,性格翻个身 get 然后我现在可以这样定一个 t 啊 t 奶茶等于什么呢?啊? 那咱先想吃火锅对吧?先想吃火锅,那就是 pot hot 等于什么呢?等于偶喂他,大家看啊,偶喂他,后面写一个 get。 好的 pose。 大家还记得这个盖的好的炮的返回值是什么的吗?刚才咱们写的盖的好的 pos 咱说的他的返回值是不是一个普洱密室对象啊?我们看一下盖的好的 pos 里衬一个牛普奥密室, 也就是说在他的值是一个普奥面试对象,我在为他后面加一个普奥面试对象就可以直接实现什么直接把 resow 传出来那个数据复制给前面这个字,这句话能理解吗?直接获取 resow 传递出来的一部数 数据,这句话能理解吗?就是我为他后面加一个普洱米斯对象就直接能拿到鬼兽传出来的数据就不用瞪了啊,刚才咱得瞪才能拿的到对吧?刚才咱得瞪才能拿到,我现在不用瞪了,我直接我喂他就能拿的到了啊。对的对的,就看起来更像是同步的戴帽啊。所以我现在可以说的那个叔叔,这个好的炮 咱们看一下啊,然后我调用这个该他对他括号,我调用这个呃性格函数,然后让我性格函数拿到这个火锅,我们看一下效果,刷新两秒之后拿到火锅了,然后我下面再写一个,咱是先拿火锅再拿奶茶,对吧?来次 t 等于 ovax 括号,然后可以说点 bug 呃 t 再刷新,大家看火锅奶茶拿到了。 那这样大家看啊,这个代码是不是就清爽了,比刚才的什么毁掉啊,比刚才的这个普洱密室啊,就是舒服很多了是吧。啊, 我这看起来跟同步代码一样,先执行第一行,再执行第二行,再执行第三行,再执行第四行啊,而且说这是异部的异部获取异部的数据啊,我看起来更像是同步,因为他异部会等待,等着你啊, 我为他等待,等着你执行,拿到数据我再往下面执行,这就是终极的解决方案性函数来解决一步问题,然后把这个一步的程序呢写起来更像是一个同步的程序。
888晓舟报告 02:11
02:11 02:06查看AI文稿AI文稿
02:06查看AI文稿AI文稿作用在这个赛恩上,他依然是他的本正函数,依然是算服 a 的本正函数。好吧,对议可观测量完全集一个物理系统,那个,如果两个算符是可对议的话,他们就拥有 一组共同的本程函数集。或者说,如果他们拥有共同的本程函数集,他们两个是可对议的,就说充要充分条件和必要条件,就说由 a 到由由,由这个一个 前提到另外一个前提,从事另外一个钱就再反退回来,这样他们两个是等笑的啊,相等的。也就是说两个算服的可对议和他们拥有共同本正函入级是同样一回事。那么我们来证明一下这件事情啊, 假设算服 a 的话和算服 b 的话是对义的,我们要导出他拥拥有共同 拥有共同本征函数啊,本征函数及阿根斯蒂多人。那么怎么证明呢?假设呢?如果是一个一个函数呢? n 呢?他是这个算负 a 的本征函数啊, 阿尔法,嗯, ok, 假设这个在 n 的话,他这个在这个本正函数,而在每一个阿尔法 n 呢?值的话,他是不减并的,就唯一的哈,唯一的不减命。如果 b 对他做了一个算作用之后,他还是不是 a 的本正函数啊?那我们就只需要看检查他是不是 a 的本正函数,那就是 a 在 b 给他作用以后,看看他还是不是 a 的本正函数啊。那这个 b 和 a 呢?是可对 e 的,所以呢,我们可以写成 b 的 a 的 sine, ok, 那这个显然就是 r 和 n, 对吧?因为标量可以,系数可以提过来啊,所以说就是 b 的赛 n, ok, 那么这一项跟这一项显然就是如果赛 n 是 a 算符的本正函数,那么 一个跟他对义的算服 b 作用在这个赛恩上,他依然是他的本正函数,依然是算服 a 的本正函数,好吧?
721张朝阳的物理课 02:14查看AI文稿AI文稿
02:14查看AI文稿AI文稿好的,欢迎回来。我们刚才理解了什么是平均变化率,什么是极限,那现在我们来看一下倒数的概念。什么是倒数呢?当函数 y 等于 fs 的自变量 s, 那我们随便画一个函数,随便画一个图像,自变量 s 在 s 零处, 假如这个点是 s, 零处产生一个增量 s, 他往这边取,是不是取增量 s, 这个是 delta x 输出的一个增量,就为 delta y, 这个其实就是 delta y 这个函数输出的增量 delta y 与这个变化量 delta s 的比值,也就是 delta y 比上 delta x, 就是刚才讲的这个平均变化嘛,对吧?当 s 趋近于零的时候,如果有机械 a 存在,那我们把这个 a 就称之为 s 零处的倒数,记作 fs 在 s 零的倒数值,也就是说对这个东西其他的 极限值。那什么时候呢?当 delta x 七进于零的时候,取到它的极限值,把它的式子写出来,就是这个样子的。一个个理解。好。首先我们是要取它的变化率,那就是 delta y 除以 delta x。 第二步是取它的极限值,也就是当 delta x 去零的时候得到的这个数, 把它试着展开 s, 零加上得到 s, 是不是 f 五 s 二减去 f 五, s 一得到 s 就是 s 二减去 s 一,哈,当这个无限接近于零的时候,得到的这个极限值就是它的倒数值,这个要理解清楚。好,这个是倒数的概念, 所以我们求函数 y 等 f s 的倒数的时候,要有两个步骤,第一个就是求它的平均变化率,就是我们的 delta y 比上 delta x。 第二步就是取它的极限值, 那就是当 dota s 去零的时候得到的就是它的倒数,倒数的话,我们上面是有一撇表示它的倒数 f s 零,一撇表示它 s 零处的倒数,那 f s 的一撇,那 s 是变化的,所以这个是每一个 s 对应的倒数,所以这个东西就是导航 数,因为这是确定的一个值,所以得到的是一个值,他是倒数值,对吧?这是 s 在变化又得到了一组数值啊?所以他是一个新的函数,就是 s 对应的倒数值的函数,所以他是倒函数,这个就是倒数的概念,大家要理解清楚。
1915小明哥的数理课堂 06:55查看AI文稿AI文稿
06:55查看AI文稿AI文稿大家好,我是老吴,欢迎观看 excev b a 入门开窍课程。这节课我们来学习耐克运算符。赖克运算符可以用来比较两个字符串,以往我们在比较两个字符串是否相等的时候呢?我们可以使用等号。 如果我们要找一个支付串,里面是否包含某个支付串呢?我们可以使用上节课学习过的 in str 函数, 但是如果我们要进行一些模糊性的匹配啊,就是概念性的,我们就可以使用更为灵活的这个耐克耐克运算服。这里呢就是你需要比较的这个支付串, 然后那个运转服,后面呢?这个拍腾呢,他是一种表达式啊,就是你通过下面这种东西呢,来进行一个概念性的,让他来匹配。好,我们进入 代码的编辑界面,好,首先第一个问号,他代表着任何单一制服,比如说我现在前面是一个 excel, 然后 like, 后面打了三个问号,好,来看一下他返回了什么啊?返回了 boss 啊,不匹配, 为什么?因为我现在三个问号代表三个任意字符,而我前面是五个字符,所以他无法匹配。如果我后面再加上两个问号啊,他就匹配上了啊,如果你这边如果使用等号呢,是不行的啊, 你使用等号啊,他是会返回 pose 的,所以这个时候呢,你一定要使用那个运转符,不管你前面是什么,你就是前面是一二三四五啊,我也能匹配上啊,比如说你就是要匹配五个 制服的这种单元格,那你就可以用这个, ok, 再来看下一个,好,这个星号呢,他代表零个或多个制服 啊,比如说下面这个就写了一个这个新号,他是否哎?他成立了啊?因为他代表零个或多个 啊,你就是再多再加一点都没有关系啊,他都能匹配上啊,所以呢,他的功能就包含了这个 i s t r 函数啊,他也能做这种包含性的匹配。 我们来看看这个第三个,这就是一个包含性的匹配,就现在前面是一个支付串啊,它里面有没有包含?我,就是我的前面可以有多个字符,也可以没有,我的后面也可以有多个字符,同样的也可以没有来看是否包含 那包含。如果把这张改一下啊,比如说改成一个微啊,不包含。好,再来看下一个井号, 井号是任意一个数字啊,就是零到九,就是说这个井号呢,他针对性就更强啊,他只是任意一个数字, 他是另一个制服啊,他是包含他的啊,这个问号是包含这个井号的,来看一下这个例子。好,前面是这个制服串一个苹果,然后后面这个表达是呢?哎,这个是什么意思?这个的意思就是说我现在要匹配的是以数字开头,然 然后后面可有可无,可以有多个任意制服,也可以没有。来看一下啊,匹配上了,如果你前面没有数字开头呢 啊,他就匹配不上,那一定要有数字开头啊,哪怕是两个也没有关系啊,因为这个就代表这个, 而这个代表这些啊,都包含进去了,比如说我现在只想匹配那两个数字开头,然后后面跟着一连串的东西啊,可以有,可以没有,怎么匹配?我们把这个井号呢?再加一个 啊,就是这个制服串呢,前面必须是两个数字,然后后面可以跟制服,也可以不跟制服来看一下啊,就反过去, 如果这个时候呢,你把前面删掉了啊,能不能匹配上,那就不能匹配上,因为这个就不是一个数字,所以呢这地方就不行。 ok, 最后我们再来看一下这个啊,这个中国号 啊,就是写在这个中国号里面的,就是匹配任何单一制服啊,我们来结合这个案例来看一下啊,这个案例我们来到这里。好,我现在循环,从 a 一循环到最后一个单元格,就是循环这个区域。 好,我先把这个先去掉。好,现在我匹配的是 ss, 就是现在循环的这个一头牛,然后匹配这个表达式的意思就是说中国号里面只取一个,不是一只什么什么,或者说一头什么什么都不行。 我们先把这个去掉, 好,看一下,第一个一头牛,那就是这个一,然后头牛 ok, q 啊,第二个一只羊也是 ok 的啊,一,这个中间织 啊,一条鱼就放生了啊,为什么?因为这个中国号里面没有条,这里说了他是匹配其中的任意单一制服 三个字的,这个字不穿中间可以是字,也可以是头啊,但是没有的话呢,我就返回 boss, 好,一匹马可以吗?哎,也不可以啊,一个人可以吗?也不可以啊,就完了。好,再来看一下下一个 啊,这个呢,就是不在这个中国号里面的啊,就是在前面加了一个感叹号啊,相当于是反选的意思啊,就是写在这个中国号里面呢,反而是不能匹配啊, 现在我反过来了,我前面加了一个感叹号,就是说我现在匹配这种前面一个字的,中间呢,不是枝,也不是头,后面再有一个任意字符的这种形式。 好,那这样呢,他就完全反过来了啊,第一个一头牛哎,这个头在里面呢,我不要匹配这个头的啊,有个这样的感叹号啊,就返回 boss 啊,一只羊可以吗?也不可以啊,也是这样的,我不需要中间是枝,也不需要中间是头 啊,一条鱼搞定一匹马, ok, 然后一个人, ok, 这个耐克运算服的一个比较方式呢,我们就大致讲完了,下节 课呢,我们再利用耐克运算服来完成一个案例。好了,那这节课呢,就讲到这里,感谢各位看官的支持,如果这个视频能帮助到你,请帮忙点赞、收藏、转发。我是老吴,关注我,下节课我们将学习新的内容。
411快学excel 01:07:27
01:07:27 01:03
01:03 01:51
01:51 01:48查看AI文稿AI文稿
01:48查看AI文稿AI文稿好的,接下来我们看一下对数的运算公式,对数的话他有加减法,还有速乘,还有他的一些运算。我们先来一个个看一下,如果两个对数同底相加,就会等于底数不变,真数相乘,如果 是相减的话,底数不变,真数相处好。这个都比较简单,如果一个数乘以一个对数,这个数就可以放到对数的真数里面,当他 他的指数把这个前面的系数放到真数里面,当指数第四个 a 的落 a n 次方等于 n, 怎么去理解他呢?因为我们 a 的 x 次方等于 n, 所以我们 x 就等于多少,是不等于捞 a, a 呢?这个是我们指数跟对数的相互运算。好,我们把这个哎开始用捞 a n 代替掉,那 a 的捞 a, n 是不是这个代替掉之后,他就直接 这第四个公式比较重要,因为我有个视频是专门以第四个公式为准,然后去推导其他的公式的,你看一下我这个对数运算的合集就可以了。然后第五个底数的指数跟真数的指数,真数的指数他拿出来是变成了分子 比数的指数拿出来之后他就变成了分母,这里记一下换底公式,如果捞 a n 不方便用的时候,我们就把底数换掉,他分子就是以 n 为真数,分母就是以 a 为真数,相当于把这里切开,如果 绕 a, b 乘以绕 b a, 他等于一。这个公式也经常会使用的,通过这个公式是不是可以推到下面这个公式,然后把它移过去就得到的第八个公式。公式的话是要大家记住的,如果记不住的情况下,你就看一下我的这个公式 推倒的这个视频,在你忘记公式的前提下,你可以通过记一个公式,你就可以把所有的公式都给背出来了,这个就是对数的运算,自己多读多记一下。
521小明哥的数理课堂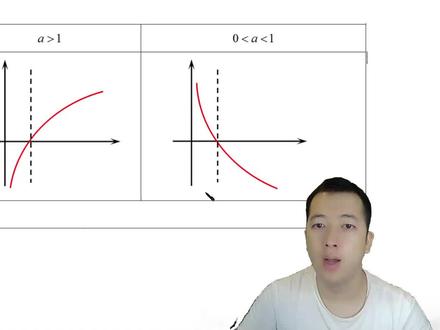 01:11查看AI文稿AI文稿
01:11查看AI文稿AI文稿好的,我们再来看一下对数函数底数 a 的变化对我们函数的影响。好,我们对数函数 y 等于捞 a x。 好,当底数变化的时候,他是怎么变化? 他的图像跟我们指数函数的图像是非常相像的啊,只是 s 跟 y 倒过来了对吧。当 a 越大的时候,我们指数函数是怎样子的? 指数函数是不是越靠近弯?所以我们对数函数当 a 越大的时候,他是越靠近 x, 这就大于一的情况下,他就越靠近 x 走。 反过来,在零到一之间的时候,当 a 越小的时候,他就越靠近我们的 s 轴。好,最好理解清楚就可以了,自己可以记一下,然后看一下书本上的内容啊。那我们做一下小结。对数函数我们一样的跟指数函数一样,我们要理解对数的运算是怎样子的,函数的限制就包括他的单调性, 值域,定义域,还有他横经过的点,还有 a 对图像的影响。图像的这些性质非常重要的 题目的话,我有专门的一个对数函数的特技啊,里面有分了好几个对数函数的题型啊,自己可以看一下,这里就不再讲题了。好,这个就是我们对数跟对数函数的内容,自己多巩固一下。
297小明哥的数理课堂
猜你喜欢
最新视频
- 8232云影同学






