张旭2.0小号开播时间
粉丝36.1万获赞21.4万
相关视频
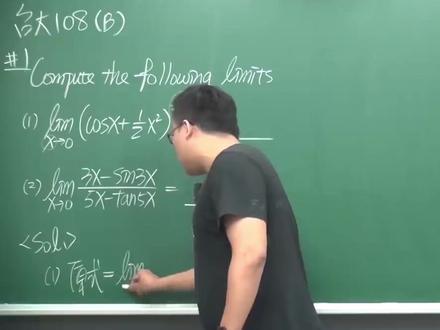 06:27查看AI文稿AI文稿
06:27查看AI文稿AI文稿好,各位同学好,我是张学老师,那今天呢,来帮大家解说这个台大转学考为积分一零八学年度的 b 卷。那这是第一题,那第一题教我们算什么东西呢?教我们算这个 limit 就是极限,那这边有两题极限哦,那我们来看一下这个极限在问什么题目?他说第一题呢,是算这个口上 x 加二分之 h 平方等 h 四四万分之一,他这个 h 区近于您的极限。 好,那第二题的话呢,是三 x 减掉赛三 x 除以五 x 减掉天卷五 s 这个题目的极限,那这两个题题目呢,它的极限 x 都是趋近于零。 ok, 好,那这两个题目呢?啊,特别来讲第一题的话呢,它看起来很复杂,实际上很简单,为什么呢?因为我们只要看到啊,这个翅膀刚好这个有一个 x, 对不对?刚好就是前面这个 x 的话呢,那通常我们使用的方法都是使用到换体公式,就是取 ispo 内缺 log。 好,那我们来试试, 看好到底怎么操作。那这个取 is pronational logo 的技术呢?倒非常熟练哦,因为这个考试的话,基本上都是非常常用的。好,怎么做呢?来 limit 还是 limiter, 但是把里面的四字呢,改写成 is pronouncial logo, oh, it's bone, 就是 log, 这个动作要做的非常的熟练。好口算你的 x 再加上什么二分之一 x 的平方,然后 x 的四四万分之一。 ok, 那这样做有什么好处呢?他的好处就是啊,这个厘米扯,一旦碰到这个一的时候,是可以直接丢到上面去的,这是第一个好处。第二个好处呢,是这个 s 的四四万分之一呢,可以透过 logo 呢,把它拉下来。好,所以做这个动作呢,同时可以 处理两件事情,可以吧?好,所以它会变成什么东西呢?它会变成 is penetry, 然后 limit x 区进于零。那这个拉下来之后呢?哦,因为 s 四四方分之一,这个 s 四四方是在分母, 所以他整个整理完之后,就变成什么 s 的四次方分之 logo 的科赛的 x, 再加上二分之一 x 的平方, ok, 就长这样子。好,那遇到这样的题目呢,其实已经比原本的式子简单多了,因为原本的式子呢,它是底数跟指数的地方都有,这个 x 会比较麻烦。那现在呢?透过去 easy 国内去 logo 呢?它变成什么?只有分子跟分母有 x 而已啊,那这是分字型, 分式型的话,第一件事情要检查的就是他有没有这个满足不定型嘛,因为使用如果是满足不定型的话,就可以使用罗必达法则。好,那你看这个 s 区近于零,所以他的分母趋近于几,是不是趋近于零,对不对?那分子的部分呢?分子的部分 s 区近于零的时候,这个趋近于一嘛, 那这一项呢?趋近于零嘛,所以整个来讲,上面趋近于什么?露个一,趋近于露个一,就是趋近于零。 好,所以整个上面呢,它是趋近于零的。 ok, 好,那它上面趋近于零的话呢?好,那我们这边上下都趋近于零,就可以使用罗必达,那我在使用罗必达的时候呢,这边都会写一个 l 号,这就是使用这个罗必达。在这个等号上面, 有些老师可能会是用这个三角形,或者是用个点嘛,那我这边使用 l, 那就看你们教授是教哪一种版本哦,你就使用那个符号就对了。好,那使用罗必达之后,罗必达就是呢,分子为分,分母也为分嘛, 所以在这个极限的部分呢,来,分子的为分,分母的为分。怎么为嘞?来,各位,分子的为分,分母的为分。先看分母,分母比较简单。对,因为分母的话是 h 的四次方嘛,所以他为分为下去之后就变多了,变成四 h 的三次方。 好,变成四 s 的三四方。那分子的部分微分 log 的微分就是什么?就是里面这个东西分支里面的微分。 好,所以里面这个东西叫做蔻赛 x, 再加上二分之一 x 的平方,而这个里面这个东西的为分是什么呢?就是复赛 x, 然后呢再加上来这个的微分就是 x, 对吧?因为翅膀拉下来跟二分之一约掉,翅膀减一,随便一次方。 好,那病人这样子之后呢,来注意一下,病人这样子之后呢,你要做适当的把它做适当的分配哦,不然会比较难算一点。那这边要怎么算会比较好呢?来,各位,这边的话呢,仔细看一下哈,这个赛跟 x 把它放在一起,那这个口赛的部分呢?跟二分之一 h 平方自己放在一起,为什么?因为这一项他的极限并不是零。 好,这两项的话极限视力好,所以把它分两边放,它会变成 exponential limit x 曲径于零,对不对?然后这边的话呢,就会变成是来,我们把这个先写 co 上一的 x, 再加上二分之一 x 的平 方。好,那这边的话呢,我们就分之一,另外一边的话呢,就是四 x 的三次方,然后这边是负算 x 的,再加上 x, ok, 就变成这样的一个极限。那变成这样极限的时候,各位注意一下这个人的极限。好,这个人的极限是一,对不对? 这个人的极限是零嘛? ok, 对吧?因为 s 区经营这极限是零嘛?所以呢,最后这边的极限其实整个来讲的话是一好,整个极限来讲的话是一 好。所以只有这边的极限和问题,那我们就单独处理这边的极限,为什么?因为这边的分子跟分母的极限都是零,你看这个,这个极限是零,对不对?这个也是零,对不对?这个极限也是零,对不对?所以零分之零,他又是不定型。那么两个相乘的极限,如, 如果要能算的话,这边的极限存在了,就要算这边的极限嘛,所以我们单独的算算,看这边的极限是多少, ok, 那一样我们使用罗必达法则,他会变什么?他会变成是 let me s 区近于零嘛?来,上面把给他罗必达,上面罗必达就是复口赛 x, 再加一下面罗必达的话,就是三层下变十二 h 平方。 ok, 好,那这个时候呢?来再看一次哦,这个地方曲径于零的时候,这个地方是负一啊,这个地方是负一。 好,因为前面有个负号,所以负一加一又是零,那下面的分母又是零啊,再一次,罗必达,对不对?所以再罗一次。好,罗一次不行就给他罗两次,他就变成了 limit x 区禁于 零。好,然后呢?这边是什么呢?这边是口晒的维分是负晒,所以变成晒,然后下面呢?变成二十四 x, 可以吧?好,那这个时候就很简单的,为什么?因为我们都知道,当 s 区近于零的时候, x 分之三, h 这一项区近于一, 所以最后啊,这个极限就多少?二十四分之一乘上一。好,二十四分之一。 ok, 结束。所以这一项这么复杂的一项,其实他趋近于二十四分之一, 所以最后的极限就是什么呢?就是一次普天学,然后上面呢,他的极限是一乘三二十四分之一,最后答案就是一的二十四次方,二,一的二十四分之一次方啊,这就是答案。 ok, 好,那这个题目呢,基本上就是做适当的配象,然后做罗必达,这样就行了。好,那我们马上来看一下。
8992数学老师张旭-索多玛分站 04:11
04:11 01:09
01:09 02:30
02:30 00:30
00:30 03:02
03:02 00:11
00:11 00:08
00:08








