感情重叠是什么意思
粉丝2611获赞9.2万
相关视频
 00:41查看AI文稿AI文稿
00:41查看AI文稿AI文稿一个爱捡垃圾的人,绝不会因为一个小垃圾而放弃整个垃圾堆的。这个世界上是不存在无缝衔接的啊。因为两个人从认识,然后到相知到暧昧到走到一起,需要时间的 无缝衔接的话,他们认识的这个时间,他消失了吗?其实没有。事实上没有无缝衔接,而是这两段关系发生了重叠。也就是所有的无缝衔接,其实都是预谋已久。如果你被无缝衔接了,你完全不用担心,因为他们在一起不会长久。 一个爱捡垃圾的人,绝不会因为一个小垃圾而放弃整个垃圾堆的。哪怕他们修成了正果,你也不用担心啊。你只能祝福他们,因为垃圾分类做的真好,真的绝了。
481周渲智老师的情感疗愈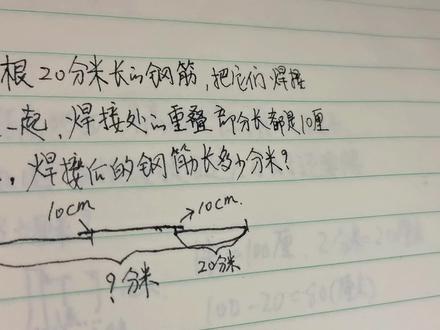 03:33查看AI文稿AI文稿
03:33查看AI文稿AI文稿欢迎大家来到外婆课堂,今天我要讲二年级应用题,请看题。三根二分米长的钢筋,把他们焊接在一起,焊接出的重叠部分长都是十厘米,焊接后的钢筋长多少分米? 好,咱们请看图啊,也就是说我们焊接到一块了以后,他整体多少长,也就是多少分米, 单位为的是分米啊,那么他三根看到吗?他重叠部分呢?是十厘米,重叠部分十厘米,每根长是个二分米。 好嘞,家长到这以后啊,再按个暂停键,问孩子们一下啊,首先问他们一下重叠是什么意思,看他们理解了不 啊,这是一个,另外呢,问问他们这个用不用换单位啊?就是变换单位,你看最后问的是啊,焊接后钢筋长哎,多少分米? 这里边呢,也是写的是分米,这问的最后,这啊都是分米对不对?问问他啊,看看。他说,哎,怎么办啊,能知道不啊?好,还有我们重叠纹,这是十厘米,他单位不一样了啊,你们看,好啊,这点我们要理解了,那么咱们就好办了啊。 好嘞,嗯,如果不会的话,看我怎么讲啊,看,认真听讲,听老师讲啊。好嘞,首先呢,第一点,重叠,也就是说,哎,就说我们这两部分,就说,哎,看到吧,穿插了一下,看到吧, 穿插一下,是不是有个接触点呐,对吧,这样焊住了就对不对?所以他叫啊,重叠部分,一定要理解这点啊, 好,第二类,是不是我们把他重叠部分的十厘米我们都转,都转变成分米啊,因为他问的是分米,所以第一步我们怎么样就开始写啊,写什么写, 十厘米等于多少分米啊,是不等于一分米啊? 啊,分明是不是 dm 了呀,对吧,这个知道了以后好,那么就好说了,底下我们假说,刚开始啊,我们小的时候不考虑重叠啊,加上三根,咱们这摆到这,摆放到这都是一样啊,不重叠的,我们是不是该?是啊,哎, 二十厘米,三根啊,二十厘米,我们是不是用用这个什么呀?用乘法呀,哎,三根我们乘以三行了啊,是为六十呀,对吧?六十米啊,这是不是分米啊? 因为一根是什么?二十分米的,对不对?好,你看是不是重叠部分,我们现在再说重叠,这是重叠了以后我们是不是重叠了一个一分米, 哎,十厘米是不是一分米,这充电是不是也是个一分米?你看这两块是不是在一个算长度,另一个不算呀, 对不对?所以呢,我们得减去二分米啊,把两个重叠部分去掉,是他总长了,也就怎么办呀,也就是六十分米啊,减去二分米等于五十八分米。 好,记得最后写上打啊,把打写上好,同学们会了吧?会了,记得给老师点个小爱心哦,谢谢大家收看。
30外婆课堂 03:38查看AI文稿AI文稿
03:38查看AI文稿AI文稿今天要给大家录一个课程,是教小朋友们怎么去认识重叠关系啊。一节课的主题就是有表情的瓶瓶罐罐啊。这个 ppt 我觉得是很简单的,你们自己做就 ok 啦,不要问我 去找一些不同表情的图啊。那么我们在上课的时候呢?就可以比如说请不同的小朋友上来做一个表情。完了之后,让下面的小孩子就是呃,直接现场画,把他们这个表情的样子啊,就是给他嗯画出来啊,笑的时候是什么样子的,愤怒的时候是什么样子,惊讶的时候是什么样子。 这些是一些很可爱的一些啊。女孩子看到这些就会觉得啊,好可爱呀,哈哈哈。而且你也可以啊,你也可以让小朋友们上来哎。比如说随便点一个哎,让小朋友们来做一下这个动作对不对啊。这个东西简直就像是一个表情管理课啊,教小朋友们如何打开自己的五官,做各种各样丰富的 表情。刚刚说完的表情啊,那么我们接下来要讲的就是这个罐子,也就是说哎,比如说刚刚我们不是在纸上已经画了一些表情了吗?那么请在刚刚的这个表情上,外面再给他加一个罐子。那么老师们可以拿一些各种各样不同造型的瓶瓶罐 给他们去看啊,让他们相爱,让他们写生了啊。就是这个罐子怎么去表现,怎么去画线条,怎么走,他是长的还是胖的,还是高的,还是矮的?一二年级的年龄段稍微高一点点的,那么你可以让他画一些这种立体的,稍微偏一点点立体的啊。 那么当然了,年龄段低的话,那你就不要去强求这个东西啊,不是他们自身体验的东西,强加反而会有一些不好的。拔苗助长吗?对不对?不好的影响啊。 给小朋友们把这些不同造型的瓶子做一个啊,重叠啊。什么叫做重叠?小朋友们,什么叫做重叠?这是什么啊?一对不对啊,这是什么?哈哈。啊,也是一, 这两只两根手指啊。好,这样子变成什么呢?交叉吧,对不对啊?这是两根手指的交叉啊。那么如果说老师再把这个一,比如说把它放大一点啊,把这个物体放大一点,两张纸是两个长方形啊,那么这两张纸现在是这样子啊,并列的好,老师给他过来。哎,这样子了好。那么 现在这个角,我们看他的这个角是不是被绿色的挡住了,你现在是不是看不到了啊,这个就是重叠了。你可以让小朋友们啊,立即马上把这两个长方形重叠的样子给他画出来啊,你可以去这样子让他啊感受一下这个重叠关系啊,重叠关系。 同样的道理,我们再拿两个瓶子,让他去理解一下这个重叠关系啊,我们这边小朋友画的哎,看到没有啊,瓶子的重叠哦。啊,瓶子的重叠,而且必须要求有不同的表情。再来一点, 怎么样让这张画面更有趣,引导他们什么呢?就是想象一个场景,想象一个场景啊。就是比如说深夜晚上,当整个世界人们都人人类都入睡了。哎,超市里的啊,瓶瓶罐罐,他们都睁开了眼睛,变成了一些小妖精来,他 就出来像那个玩具总动员啊,我说你们有没有看过玩具总动员啊,然后这些瓶瓶罐罐都变成了一个小妖精,然后他们就开始玩了啊,那么夜深人静的时候啊,除了这些瓶瓶罐罐,比如说我们也可以加入一些晚上出没的动物,比如说小猫,蝙蝠等等,对不对?小精灵幽灵啊,给他开个 头,然后呢,让他自己去编故事,自己去想。那么他的画面绝对不仅仅只是一些瓶瓶罐罐那么单调了啊,他可以更丰富。在这个小巷里,真的是需要去激发的啊,你就给他一点点,他都能够反馈给你更多啊。那你的这个啊,课堂的这个感觉就好了啊。就 就就进入了非常正确的,非常正确的一个一个一个美术课堂,真正起到去啊,开发呃,孩子们创意力,创造力的一个课堂。 ok, 好期待你们啊!呃,画出更好更有趣的作品。
801青早画舍 07:49查看AI文稿AI文稿
07:49查看AI文稿AI文稿今天我们来讲讲黑板上这种类型的题,题目的要求是求下面一亿部分的面积单位是厘米。这是哪种图形呢?应老师先举一个简单的例子,大家看一下。在课间的时候,老师在黑板上画这样的图, 这是一张 a 四纸,就是个长方形吧,就是原来这个长方形的位置在这,然后呢,就把它向右平移,平移到这个地方,那你看,平移前在这个地方,对,平移后在这个地方,那中间就有一个部分,干什么了?重叠,喜欢那个词,大声说重叠,对,这一个部分就是重叠的部分, 他重叠了,什么意思?重叠是什么意思?叠在一起,哎,叠在一起两张,哎,这两张都是 a 四纸,哈,这两张叠在一起,中间重叠了,对不对?好, 那也就是说他既是左边这个长方形有的,也是右边这个长方形有的,那么有了重叠,就有一个很特殊的东西在里面了。嗯, 这个部分是重叠,我们给它标一下,这一块长方形叫做一号,中间重叠部分叫二号,而右边叫三号,一号他就等,一号他就等什么?一号他就等。好,老师写出来,你们说要写这哈一和三的面积相等,为什么呢? 因为一加二,因为一加二等于这个长方形的面积,你看,也就是说两边加一个 r, 这边也加一个,要加重叠的部分,对不对?你看,一加二 等于三加二,然后再把二给同时干嘛减去,那就是一等于三,懂了吗?好,这是这一种最简单的,最简单,最简单的就长方形拿来移嘛。那么现在放到这种图里面,其实道理是一样的,刚刚是长方形 在那移动,对不对?现在大家看这个图是什么图形?在移动?梯形啊,把那个梯形描一描,手比划一下那个梯形长什么样子。 好,老师,克隆一个出来,我给他换一个颜色,哎,这个颜色,大家看是这个梯形往哪边移?手比划, 看同学们在笑,往下移,是不是移到这个地方来了?再看一次在这,然后移到下面,好,他可以走了。哈哈,好了,那我现在来讲,那么重叠部分在哪里?描出来 在哪?哦,在这,非常好,李老师现在特别喜欢现在下面听课的状态,这是重叠部分,咱们给他标上叫几号? 二号。行,那,那有二号,肯定前面有一号,一号在哪?你们想在哪个地方?一部分啊,一部分。好,老师,继续瞄。老师,换一个颜色吧,换个蓝色。行,这个上面阴影部分,你们说叫什么名字?一号,你们说的是叫一号, 那下面这个叫什么?三号,这个叫什么?三号,这个叫。这一部分叫三号。好了,马上能得出什么 一点三,一点三,什么一点三?你们说一等于三,为什么一等于三呢?因为一加二加二等于二加三,一加二等于二加三。我们来看看为什么 一加二是不是等于一个梯形的面积?二加三也是一个梯形的面积,是这两个梯形的面积,干嘛一啊?然后根据等式的性质,刚刚你看你老师现在可喜欢咱们班听课的状态了, 你看,当同学们认真思考的时候,他就能想想到以前知识的联系。前面才觉得等式的性质,两边同时干嘛减二,两边同时减二,那就得到了一等于三,而我们要求一号图形的面积,其实就是谁的面积? 三号,三号是一个什么图形?梯形,梯形支到下底支到高,那还差一个什么?上底是好多十 十,怎么解释?因为这是下底吗?十三减三,这里是十。好,上底咱们先写下,看这老师计算的时候,当上底不知道,我们先算十三减。哦,老师写错了哈,十三减三等于十厘米,然后在计算面积的时候,一个公式写出来, 上底加下底的和乘高除以二。好,这里算出来是四十六平方厘米, 这是左边这个几,这一下就清晰了。今后看到这种重叠部分,咱们先找重叠的那个地方在哪?这是二号重叠的,那么我们接着来思考,右边这个图形,看成叠部分在哪里 在哪里?好,行,老师你要出来,在这个地方,这是重叠的部分,咱们给他叫上二,重叠的我们都叫二。 行,那左边这一块我们叫什么?一,还有一部分三,哎,这个一部分我们就叫做三,当然,你看这个梯形三吗?这个梯形它是一部分,我就想如果能直接计算出来,我可以直接算,不能的话就要转换一下,是不是?我们来看看能不能算,不能上底在哪里? 那你二在哪?就在这下底在这,上底不知道,下底也不知道,高也不知道,直接算,算不出来。转化重叠来 看,找到重叠部分了,马上能得出什么?一等于三,因为一加二是三角形的面积,二加三也是三角形的面积,它们相等,再把二给同时减去, 就得到了一等于三。我们要求三号的面积,其实只需要求出一号的面积,因为他俩的面积相等,那咱们来求一号的面积,大家看一号图形是个什么图形?梯形,梯形的上底在哪? 老师有个问题,怎么找梯形的上底和下底转过来,还有听老师提醒大家如何找梯形的上底和下底, 那么他的上底和下底是一组平行边。上,这里的这句话听懂了,女生 t 型的上底和下底是一组平行边,所以我们找平行边是在这,那么这两条边就是上底和下底,短的那条边是上底,长的那条边是下,懂了吗?上底和下底就是平行的边。 好,现在上底知不知道算算好多八减三哦,这,这一段是三,那整个是八,那上底就是八,减三等于五厘米, 下底知不知道知道多长八高呢?五。然后咱们再来求面积,上底加下底的和乘高除以二。好,这里就算出来计算的问题,这个是三十二点五平方厘米, 这个图老师画的有点不标准,那个五,那个五跟那个五上面和那个高图是一样的。哪里哦,你看老师画的这个上底和这个五的距离都一样,所以好,老师请写自我批评。那我下次画图的时候注意一下,就跟你们说,这里上底是五,这个五明明比这个五要长那么多,哎,对老师这个图画的不标准,大家同学们方法听懂了吗? 好,今后老师画图的时候还得注意,因为咱们班同学火眼金睛,经常喜欢发现老师的问题,非常好。那你们看一个老师画的图,就觉得我一下画的不标准,你们画是一图的时候,也许你们画标准哈,那我的眼睛也是很雪亮的哦,我就问你这个, 这个是比例是不对的,我也要说你们哈好,同学们,坐在这,坐在这,咱们来总结一下这类型的问题,咱们给他起个名字叫什么问题这边有写的,我们就像重叠问题。 那是什么重叠呢?是两个不一样的图形拿来重叠吗?一样的,是两个一样的。对,这种问题一定是两个完全相同的图形, 拿来干嘛?重叠,对不对?两个完全一样图形重叠,那么他们做这种题的方法就是找出重叠的部分,两边的就相等的,听懂了就上,就是解这种题的关键。
8428顺顺的小太阳 01:24查看AI文稿AI文稿
01:24查看AI文稿AI文稿怎么看待分手后的无缝衔接?无缝衔接是什么意思?你的手放开的那一刹那,他就做了别人的事,你还在恍惚?前几天说分手是真是假,他今天就在朋友圈做了一些关心。 别傻,哪有什么东西,有的都是提前对接重叠相接罢了。 从相识到相知到暧昧,这个过程他不需要时间吗?这个时间无非就是和你在一起的时间重叠了而已。可是同学们, 你们回头看看自己这一路走来,你是真的被假爱迷惑到晕头转向无法分辨?还是你根本不愿擦亮眼睛看清楚这明目张胆的蛛丝马迹呢?这个答案你心里清楚, 因为没有人会突然不爱你,只是你突然发现了,这个世界就是这样,有些人笨到擦干眼泪继续爱你。有的人精明到权衡利弊后放弃你。但凡你们需要明白,二选一,被抛弃的那个人才是你。 三忍,谁先锤谁,最后我相信,风水轮流转,今天你会赢。
16曾经的她 07:08查看AI文稿AI文稿
07:08查看AI文稿AI文稿hello, 大家好,今天我们来看一下一半模型之重叠等于未覆盖,所以看到这个题目哈,重叠等于未覆盖,说明我们今天要讲的是一个等量关系或是一个啊 结论。那我们首先来看一下什么叫做重叠等于未覆盖。那实际上重叠等于未覆盖指的是当同一个图形当中含有两个一半模型的时候,也说有两个图形同时都占这个整体图形的一半的时候,那这两个一半模型重叠部分的面积就等于他们啊 未覆盖到的面积,这个我们称之为是重叠等于未覆盖。那我们接下来从我们的图形当中来具体的或者详细的讲解一下,为什么重叠面积就等于未覆盖的面积。那么来看一下我们重叠等于未覆盖的图形哈,然后再从图形当中来讲 它的原理。首先来看我们长方形当中或者平行四边形当中的一半模型,那我们最基本的平行四边形当中的一半模型是这样一个三角形,绿色三角形是我们整体长方形面积一半,同样的这个粉色三角形面积也占整体长方形面积的一半,所以这个长方形当中同 同时还有两个一半模型,所以这两个一半模型他们重叠部分的面积是这样一个 红色的四边形的面积啊,而未覆盖到的面积数就两个灰色部分的面积。所谓未覆盖到,就是啊, 整个长方形当中除这两个一半模型之外的部分,我们称之为是啊未覆盖到的部分。那为什么重叠面积等于未覆盖的面积呢?我来想一下哈,因为我们绿色三角形和粉色三角形面积各占长方形面积的一半,那就意味着 这两个三角形的面积之和就恰好等于长方形的面积。换句话来讲,如果我们把这两个三角形不重叠的 平铺到这个长方形里面,那恰好能够把整个长方形面积完全覆盖,因为它面积是不是相等的,所以是不是恰好能够完全覆盖,而现在实际上是有两个三角形,这两块地方没有覆盖到,而没有覆盖到的原因是这两个三角形是在这重复了,重叠了,因为重叠就意味着这儿是 把这个面积是铺了两次,在这一块地方是有一次浪费的,所以重叠面积就等于未覆盖的面积,所以这是我们这个结论的由来哈,那这是我们在平行四边形当中的一种重叠等于未覆盖的类型,那还有另外一种来看哈,所以重叠面积等于未覆盖的面积,那我们来看另外一种情况,同样一个长方形, 先找一个一一半的面积,是不是这个三角形同样我们在另外一个方向这样横着,这个粉色面积是同样占长方形面积一半,而此时他们重叠面积的中间,这个红色四边形 未覆盖的是这样三个三角形,这三个阴影部分的面积啊,所以根据重叠等于未覆盖,那红色面积就等于阴影部分的面积,那这两个是我们在平行四边形当中重叠等于未覆盖的 相关图形。那除了在平行四边形当中,我们的一半模型是不是还存在于梯形当中?所以在梯形当中我们要找一半模型, 首先在找到一条腰的终点,然后向相对的顶点连一个三角形,所以这个绿色三角形占梯形的一半,这个粉色三角形也占梯形的一半,而他们重叠的面积就是中间的这样一个红色的 四边形,而未覆盖的面积是上下两个三角形,所以重叠面积就等于未覆盖的面积。那我们再来看一下我们任意四边形当中的一半模型。我们在任意四边形当中要找一半模型,是要在相对的两条边上各取一个终点向这边连线,所以我们这个 绿色的这个四边形所占的面积是整个整体四边形面积的一半,同样这个粉色的四边形面积也占整体四边形面积一半,而这两个四边形,这两个一半模型所对应的重叠部分是中间这样一个红色四边形啊, 未覆盖的部分是左右两个阴影部分,所以重叠面积就等于啊未覆盖的面积。那我们除了这样的形状之外,在我们的任意四边形当中还存在这样的重叠,等于未覆盖。首先同样一个 半模型,绿色数占一半,另外我们在另外一个方向或另外一组对边上面再找两个终点,是不是得到这样的一个一半模型,红色面积,粉色面积数占整体四边形面积一半, 所以这两个一半重叠部分是中间这样一个红色四边形啊,而未覆盖的就是四个角上的四个三角形的面积,所以重叠面积就等于啊未覆盖的面积, 这个就是我们重叠等于未覆盖所对应的图形,它本质上是在同一个图形当中两种一半模型的一个组合,或者说是啊, 回家,那我们的这个结论或者是这种图形讲完了,接下来我们再来看一道题目哈。来看这样一道题目,说如图所示, e、 f、 g、 h 分别是四边形个边的终点, e、 f、 g、 h 四边形 a、 b、 c、 d 是不是有任意四边形啊?分 别是个边、中点四块阴影部分的面积分别为一、二、三、四,所以这个是一,这个是二,这个是三,这个是四,是大概这个样子啊。然后则四边形 o、 n、 m、 l 的面积是,所以 o、 n、 m、 l 是问中间这一个四边形面积啊,所以那我们来看这个题目哈。首先在这样一个任意四边形当中,我们有四个点是不各式分别是各边的终点,那既然 e、 f、 g、 h 分别是四边形 a、 b、 c、 d 各边的终点,所以我们就能得到一个结论。什么结论呢? 第一个, a、 j、 c、 e 和 b、 f、 d、 h 这两个四边形的面积一定是 a、 b、 c、 d 这个大四边形面积的一半,因为这两个四边形所对应的一定是一半模型的四边形,所以我们来看一下 a、 j、 c、 e 和 b、 f、 d、 h。 首先来看 b、 f、 d、 h 是这样一个红色四边形的面积啊,它一定占整体大四边形面积一半,那我们要证明这个一半模型,我们只需要连接 b、 d 数就可以证明啊。那关 关于我们任意四边形当中一半模型的证明,大家可以回去翻我我讲过的其他的图形,其他之之前讲过的已经发过的视频哈。那这个粉色面积是占我们任意四边形面积一半, 同样的 a、 e、 c、 g 这个绿色四边形,同时也是我们 a、 b、 c、 d 这个大四边形面积的一半,连接 a、 c 数就可以证明啊。那既然这两个都是一半模型,所以我们就有一个结论叫做重叠等于啊 未覆盖,重叠面积等于未覆盖的面积,而他们两个的重叠面积是不是就是中间这个红色四边形,也就是 o、 n、 m、 l 这样一个四边形,对吧?所以我们要求 o, n, m、 l 的面积只需要把四个未覆盖,是不是这四个灰色三角形面积啊加起来就可以了,所以那重叠面积就等于一加二加三加四就等于啊 十,这就是我们的这样一道任意四边形当中重叠等于未覆盖的题目,所以只要你能够把图形看懂了,那这道题目就变得非常非常的简单。好,那我们这道题就要讲完了。
230小升初数学李力老师











