欧拉公式专升本浙江
粉丝8.8万获赞63.6万
相关视频
 03:26查看AI文稿AI文稿
03:26查看AI文稿AI文稿高斯曾说,一个人能否感受到欧拉公式的魅力,决定了他是否有成为数学家的潜质。数学家们评价他是上帝创造的公式。欧拉公式凭借一己之力打通了指数函数、三角函数和复数的壁垒,让求导和积分变成一个简单的、不能再简单的问题,尤其是对于微分 方程来说,那公式将为打击。今天我们就来学习它。首先,我们要知道,欧拉公式既不是公里,也不是独立于定义的定律,它是时数域上的指数函数通过密集数解析沿透到负数域后自然导出的恒等式。而欧拉公式的具体定义如下,对 任意时数艾克斯都有一艾艾克斯方等于寇塞因艾克斯加艾塞因艾克斯。注意了,这里的每一个符号都有严格的定义, 这里的一是自然常数,爱是虚数单位满足爱的平方等于负一口塞因艾克斯,塞因艾克斯则是三角函数。那在了解了它的定义后,我们来看一下是如何从密集数中 推导出欧拉公式的吧。在正式推导前,我们需要引入指数函数与三角函数的密集数展开式。而之所以要引入这些密集数,是因为他们就像一把钥匙,打开了欧拉公式推导的大门。从本质上看,密集数为指数函数和三角函数提供了一 种共同语言,使他们能够在同一数学框架下相互对照,彼此转化。接下来只需要三步,就能完成整个证明过程。第一步,将指数函数的密集数推广到负数自变量。因为指数函数的定义式在负数域内收敛,我们就直接将 e 的 艾克斯 方的密集数展开式中的艾克斯替换为负数艾艾克斯,那我们就能得到这个式子,这是负数值函数 e 的 艾克斯方的密集数定义式,它的意思是 我们将 e 的 艾艾克斯方定义为一个无穷级数的核,而这个级数的每一项是连得阶乘分之艾艾克斯的 n 次方。第二步,艾米斯的教训拆分级数,那我们就得到了这个,接着带回到级数展开适中,从而得到这个。这时我们发现它已经将 e 的 艾艾克斯方清晰的 翻译成了实部和虚部两部分,将原本混杂的复数指数级数同组成为了我们熟悉的两个实函数的级数之合。第三步,识别拆分后级数所对应的三角函数。观察拆分后的两项,我们就能发现它们在结构上恰好 分别对应正弦函数和余弦函数的密级数。展开式,将其替换号,我们就得到了欧拉公式。到这里,欧拉公式的证明就结束了。 通过欧拉公式,我们就可以把三角函数轻易地转化为指数函数,将三角积分问题转化为更易处理的指数积分问题,从而避免了繁琐的三角恒等变化。就比如像这两个三角函数根替欧拉公式,将艾艾克斯替换为负艾艾克斯, 那我们就能得到这个。接着再加两个等式做预算,我们就可以让它们轻松转换。那在搞懂了概念定义后,我们来看看它是怎么应用的吧。以这道题为例,第一步,先利用欧拉公式替换克萨因艾克斯,那我 我们就能得到这个式子。第二步,计算指数积分,将结果带回到第一步的式子中,根据积分的限性性,我们可以得到这个。接着来到第三部分,母有理化,因为有理化的结果是这个,那么将结果带入到第二步的式子中,我们就能得到这个。然后来到第四步,展开合并同类型花钱后得到这个, 那么原始积分的结果也就出来了。瞬间秒出答案。怎么样,你学会了吗?正经的知识又增加了,我是带你成长的派毛,关注我,分享更多有用知识!
9817派蒙知识 01:36查看AI文稿AI文稿
01:36查看AI文稿AI文稿我们画一条连续的线,随意画哦,然后首尾相连,像这样。好啦,数数有多少个焦点,一二三四五六七 八九,然后有多少条边?一二三四五六七八九十十一,十二,十三十四十五,十六,十七十八。再数数有多少个面,一二三四五六七八九十十一。 哦,对了,最外面的也算一个区域哦,我们用焦点减去边,再加上面等于二,我们再画几个试试看, 都是这个结果。哎,有点意思啊,也就是说,我只要知道其中任意两个数字,那么第三个数字自然就能算出来。这个规律是欧拉发现的,所以也被称为欧拉公式。 欧拉一笔画定理,他有许多非常有趣的应用,像科斯堡七桥问题、最优路径问题、拓补学等等都是以他为基础的。不过不知道大家注意到没有,刚才我们的画图是在平面上的,而且是一种全覆盖哦。我想请问 像这样的全封闭的多面体算不算一种全覆盖呢?他是否也符合欧拉定理呢?把平面和立体的结合起来思考,这就是三百年前从二维过渡到三维的数学思维,欧拉牛。
62.3万爱思考的乌鸦 04:43
04:43 03:59查看AI文稿AI文稿
03:59查看AI文稿AI文稿欧拉公式,像正方体、长方体、三棱锥这样的图形是由一些平面图形围成的几何体称为多面体。简单,多面体中顶点数我们用 v 表示,面数我们用 f 表示,棱数用 e 表示,它们之间有何关系呢?首先我们来看一下下面的表格, 三棱柱,它的顶点数有六个,面数五个,棱数九个。四棱柱的顶点数是八个,面数是六个,棱数是十二个。五棱柱,它的顶点数是下面五个,上面五个,所以总共是十个。 它的面数侧面是五个,加上上下两个面是七个棱数。侧棱有五个棱,所以一共是十五条棱。 令楞柱的顶点数是十二,面数是八,棱数是十八。那么任意一个 n 楞柱,它的顶点数是可以用 n 来表示的。 一个 n 楞柱,它的底面下底面一般是有 n 个顶点,同样上上面也是有 n 个顶点,所以一共是二 n 个顶点,它的面数 下,底面中每一条棱会对应着一个侧面。 n 棱柱会有,底面上会有 n 条棱,所以它对应着 n 个侧面, 再加上上下两个底面,所以面数是 n 加二,而棱数侧棱。一条侧棱对应着一个 上下两个面的顶点,所以它会有 n 条色棱,而上面和下面又隔有 n 个 n 个棱,或者说是 n 条棱,所以它总共只有三 n 条棱。 那么二 n、 n 加二和三 a 之间有何关系啊?显然,二 n 加上 n 加二,减去三 a, 是 不是就等于二啊? 答案是肯定的,这个结果是瑞士数学家欧拉证明的,它证明了简单多面体中顶点数 v、 面数 f、 棱数 e 之间的这个有趣的关系式, v 加 f 减 e 等于二,这个公式称为欧拉公式。 好,我们来看一下欧拉公式的应用。新年晚会上是我们最欢乐的时候,有时候会场上会悬挂着一些小装饰,其中呢有各种各样的立体图形, 这些图中是我们常见的一些多面体,这是他们的名称,我们了解一下就可以啊,把图中每一个多面体具有的顶点数 v, 面数 f, 棱数 e, 哎,我们都填好了啊,这个结果呢,我们记录了表中,回答一下下面的问题。 第一,观察分析表中数据,猜想多面体的顶点数、棱数、面数之间的关系式, 这个问题比较好解答了,我们看正四面体 v 加 f 减一是等于二,正方体、正八面体以及正十二面体和正二十面体它们都具备这个规律,也就是说 v 加 f 减一都等于二, 所以它们之间的关系式就是 v 加 f 减一等于二,这就是考我们考察我们的欧拉公式。 第二位,已知一个多面体的面数比顶点数大十,有三十六条棱,让我们来求一下这个多面体的面数。我们知道多面体的面数 f, 顶点位和棱数之间的关系是 v 加 f 减一等于二,在这里棱数三十六是知道的,可以直接把它带进去。而 v 和 f 之间的关系式是面数比顶点数大十,所以 零点数应当等于面数减去十,也就是说 v 应当等于 f 减十。这样我们根据 v 加 f 减一等于二,就可以列一个关于 f 的 一元一次方程, 解一下这个方程,就可以了解出 f 等于二十四,也就是说这个多媒体的面数是二十四,最后我们写上答案。
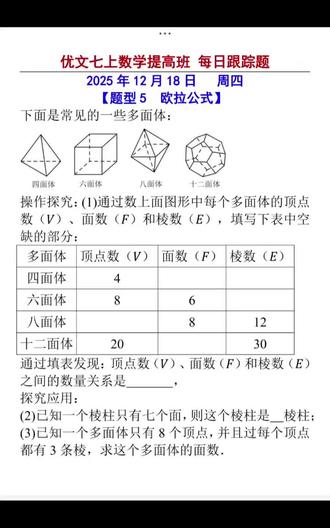 06:43查看AI文稿AI文稿
06:43查看AI文稿AI文稿大家好,我是英文徐老师,今天是十二月十八日,周四啊,心灵提高版,我们来看一下这个题型五的欧拉公式,欧拉公式就是把一个立体图形的顶点面棱数他们的关系给他研究一下。 那我们在研究之前我们数一下,呃,这上面显示的图形啊,说四面体,四面体,这个体,这个体在高中会大量的有预算题,就在高中里面这个题可能大家跟打交道的似乎特别多, 然后面数呢?四面体呢?顾名思义,四个面,那楞数呢?我们这个图我们可以数一下,侧边是三个,底边是三个,所以是六条了,然后六面体呢?六面体就是我们讲的长方体或者是正方体, 那今天都是八个,然后呢面数是六个,那楞数呢?楞数我发现上面 四个,侧边四个,下边四个啊,所以总共是十二个,然后下面是八面体, 八面体,我们看这个八面体只有六个顶点啊,这地方有个顶点,侧面四个,下面还有个顶点,所以只有六个顶点。十二面体,十二面体的面所呢?肯定是十二面, 今天说这张给了二十,然后三十,然后呢?这个满的什么关系呢?那这就是他们三个,就是这么,这个,这,这组数满的什么关系?那我发现, 呃,四加四减六,那应该等于二,然后八加六减十二,然后等于二,六加八减十二也等于二十加十,二减三十也等于十二, 所以我想了他们的买的关系呢?就是顶点数加面数减去内数等于二,顶点数加面数减去内数等于二。 那有有同学就问我了,那你是怎么分析出来了?不是我分析出来的,而是这是找规律的。题目给了四组数据,那这地方是四组数据,那我就通过这四组数据来找到一个规律, 因为一个一组数据不具有普遍性,那四组数据都满足同样的规律,那我们就寻找了普遍规律,这个普遍规律经经过总结,那就形成我们能总结的数量关系 好,所以这个顶点数是 v, 面数是 f, 减去内数,内数是一等于多少等于二,所以这一题就这样填 啊。已知一个楞柱有七个面,楞柱有七个面,那他是几楞柱?我想楞柱,哪个是楞柱?我一看这个六面体,他是楞柱,楞柱,楞柱。什么是楞柱?就是底面和顶面就有一个底面,还有个顶面, 他俩的,他俩的形状就是这个楞柱的形状。然后呢,除了顶面和底面,那旁边还有几个面,我们就称为几楞柱, 那现在有七个面,那七个面减去底面,减去底面,那他应该是五楞柱,所以这应该是五楞柱。以这一个多面体只有八个定点,并且过每一个定点有三条了, 每个顶点有三条了,那总共有多少条了?那我这样想,每个顶点有三条了,现在有多少顶点?八个顶点,所以八乘三。 但是呢,一个楞有两个定点,一个楞有两个定点,就一个楞需要消耗两个定点。那现在呢,八乘三,就是每一个顶点含有多个楞, 那现在呢,两个顶点含有一条楞,所以这个八乘三要除二才等于它的楞数。 其实呢,这地方很好理解,为什么来呢?一个顶点三条楞,然后每两个顶点共用一条楞, 那一个顶点三条楞,这个顶点乘以三,那这地方是这个顶点含有的楞数, 但是呢,总的论数不一样,总的论重合了,因为什么呢?因为你这个顶点,还有他论在另外一个顶点也被算上了,所以就重合了一倍啊,所以这是要除以二啊。所以这三八二十四,二十四,除以二应该等于十二,所以论数是十二。那问这个多面体的面数, 那我们利用刚才总结的这个公式就可以求出了面数,面是 f, 然后顶点是八,所以八加 f, f 是 面,减去 e, e 是 棱数。棱数十等于多少等于二,那所以很容易算出这个 f 是 六,那所以是六面,所以这个多面体的面数是多少?六面体或是六面。 好,这个欧拉公式大家一定要有个印象啊。 好,接着我们再往下看。好,第二题比较简单,是一个立体图形,它说棱长为二的正方形毛坯挖去一个棱长为一的小正方形,得到如图的零件,那问这个零件的表表面, 你看这个面是不是缺一块啊?那缺一块,正好这个面补上了, 然后呢,从左边看也是缺一块,那缺一块呢?在这后面这条面补上了,从上面看也是缺一块, 从上面看这个形缺一块,那也是这个面补上了啊,所以我说呢,缺的都被补上了,那还是六个面,那每个面的面积呢?还是一样的啊,所以这个表面积 s 很好做啊,每个面嫩长是二二乘二是一个面, 多少个面?六个面,所以乘以六啊,所以得到他的面是二十四啊。做到这个还不行 啊?不是做到,做到这个就行了,因为这道题没有给单位。没有给单位呢?我就不需要写单位。我以为这道题有单位写到这还不行,那这道题没给单位。他叫嫩长为一,那直接是二十四。他说这个零件体积,那体积我想了,那就是大的正方体减去个小的正方体。 挖走一块吗?挖去一块,把这个挖的剪掉,所以体积就等于总的,总的那就是二乘二,再乘二正。呃,正方题的体积嫩长乘嫩长,再乘嫩长, 减去一个小的小的是一乘一,再乘一好,所以算出来是七好。这道题还是比较简单的。
15优文培训霍 12:24查看AI文稿AI文稿
12:24查看AI文稿AI文稿之前的视频中多次用到了欧拉公式,也有同学私信我,让我好好的分享一下欧拉公式是怎么回事。那么今天我们就来好好分析一下欧拉公式。要理解欧拉公式,首先得理解数,最开始我们用到的就是自然数, 我们要数鱼补了多少条,我们要数苹果摘了多少个。刚开始的时候发现他们够用,但是到了后来发现他们不够用怎么办?有了欠债的时候,我们开始用起了负数啊,那么负整数和正整数合在一起就变成了整数, 用符号 z 表示啊,多余的负数呢?表示的意思就是减少或者说负债。而有了整数 z 发现的还不够用啊。比如说两个人要分一个苹果,每个人只能分二分之一,三个人分一个苹果,每个 怎么分三等级啊?增加了分数之后,分数和整数放在一块就变成了油腻数。我们用 q 表示吧,里面增加的分数往往表示的是分割的意思, 所以我们写的分数里面通常有一个红心啊,表示分割开来。再来看第三种,当有理数不够用的时候,有理数什么时候不够用了呢?算正方形的对角线的长度,得出根号二,他不够用了怎么办?拓展到了无理数和有理数的组合实数, 其中这个五里数典型的代表是正方形的对角线。接着啊,我们发现在球这一元二次方程的时候,出现了一个增根,而这个增根呢,可以用一个另外一个资源的数来表示,虚数 i 等于根号负一来表, 这个时候我们就拓展到了负数。 ok, 你以为这些数?我们再来理解一下为什么说实数实际上是虚数的一个表象。首先一般的一元三次方程值, ax 三次方加 bx 平方加 cx 加 d 等于零, 他都可以画上 x 的三次方,加上 px 加上 q 等于零这种形式。画这种形式之后,我们可以把它的三个根给求出来啊,求出来的四里面,我发现多了一个位置,说 w 啊,这个 w 实际上是 二分之负一加根号神癌。我们再看一下他的一个一元三次方程的一个图像,我们发现啊,他的解有可能是一 二三三个,也有可能是一两个,也有可能是一个,不管怎样,他总有一个结。 我们考虑三个解的情况,三个解都是实数解,那么这个时候我们知道 w 等于二分之负一加根号三挨,把它带到里面计算,我们会发现, 即使这里有虚数,但是他整体表现出来的还是一个时速,所以说时速 只是一个虚数的表象。从这个一元三次方程的的求中数我们就可以看出来,也就是说我们许久所认识到的一个实数,实际上只是虚数的一部分啊。理解完一元三次方程,我们再来看一看负平面上的单位元, 正常的鉴定一个 x 轴, y 轴是我们所熟悉的,当我们把 y 轴变成虚数轴, x o 变成时速轴,这个就构成了一个负平面。 如果在这个副平面里面选一个圆啊,画一个圆,单位长度是一的话,我们会发现任意点的坐标是什么呢?我们角色的角度是吉他的坐标是狂闪是一趟, i 沙也是一趟,这是他的一个坐标, 这个可以表示负平面上圆的一个坐标,你理解了这个坐标,我们再来看看负平面上加法和乘法的一个意义。我们举最简单的例子啊,一和挨在一起啊,一加挨表示什么呢?我们不知道,但是我们可以把它画出来啊。一表 的是这个点或者这个项链,从原点吧指向他的一个项链,而 i 表示这个项链,一加 i 这个点在哪里?在这里表示的是这个项链。 ok, 我们看这个加这个用平时变形的法则, 刚好就可以把这个项链给画出来,也就说一加 i 实际上是我们标个字母吧, o a 项项加 ob 项链,他是项链的一个项项,这是他加法的一个含义啊。而关于他乘法的一个含义比较理解啊,一乘以 i 一表示这个响亮,把乘以 i 变成了这个响亮啊,我们可以理解上把一旋转成九十度,我们再把这个 i 乘以 i, 发现到等于负亿啊, 在这里我们可以理解成乘以 i 又旋转的九十六万,所以说他可以表示一种旋转,但是他仅仅表示旋转呢?不只是啊,如果 i 乘以 六,哎,他就是负六了,所以说他从 i 这个单位一长度变成负六,他不只是旋转了九十度,他还身长了六倍啊。虚数相乘表示的是 长度的拉伸和角度的变化,这个长度是他到这个圆点的长度,这个角度变化也是他和圆点还有 xo 所形成的一个角度。理解的负平面的加法是项链的加法,负平面的乘法,长度的拉伸和角度的变化。 我们再来探究一下货拉公司最早是如何看出来的?是如何被发现的?首先有个叫太累的人啊,使用他的方法把三 s 给展开了,他同样把科三 s 给展开了, 接着呢,一的 x 方等于,他发现这三个数字很像,但是又有些区别啊,那这个区别到底在哪里呢?当他发现虚数的时候,他带入了一个虚数,然后每一项都带了一个虚数,最后他发现把虚步和十步写在一起, 竟然是和上面两个狮子成对应关系的红色 x 加上 id 三十。实际上这个在欧拉之前 就已经有人发现,只不过欧拉对这个公式的研究更深入,所以啊,这个事就叫做欧拉公式。他有 有哪些比较奇妙的应用呢?或者是该如何理解他呢?说到理解,他还得从一的一个本质说起吧,一是三底数,他等于根去向英雄,那的时候一加 n 分之一的人吃饭,但是他,但是当他碰到虚数 a 的时候,你的 a 吃饭,他是怎样一个减 n, 他实际上是等于 n 去 m, 那的时候 e 加 i 除以 n 等于吃饭, 那这个数字该如何理解呢?我们可以画附数平面,这个是实轴,这个是虚数轴。哀,我们可以把,恩从小到大开始取,就能发 现在的规律。比如说我们首先取这个 n 等于三,那么这个一加上 a 除以 n 的 n 次方,就写成了一加 i 除以三的三次方,这个是一加 i 除以三的一次方,他成了一个之后就变成这个点, 那成了一个之后,他变成这个点,我们会发现这个长度增大,角度也增大了。当我们把 n 取另外一只的时候, n 等于十的时候,我们发现啊,他的长度也在增大,但是增大的很缓慢,这角度也在增大。当我们取 n 非常大的时候啊, 这个是 n 等于一百,一加上二除以一百的一百之分,我们可以看到它的长度几乎没有什么变化,只是角度变化。角度变化了多少呢?这个角度将近是一啊, 也就是说 e 的 x 方等于一,加上 i 除以 n 的 n 次方。当喷去向右胸大的时候,他的这个长度半径是没有变化的,他变化的只有这个角度。 这个角度是多少呢?我们再把它写一遍,一的 i 乘以一,这就是一的 i 四方的一个几和一。你写成一的 i 四方的一个几和一啊。我们再来看一看一的 ipad, 四方的几个一啊,一的 i 四方可以写成这样, 而 e 的 ipad 脂肪同样可以写成这样。我们用相同的方法,当 n 取二十的时候,他是长度增加,角度也在增加。当 n 取一百的时候,我们会 发现他的长度几乎没了增加,但是他的角度会变得增加,这个转弯的角度就是派,那么 e 的 ipad 就很明显,他的意思就是 单位长度是一,胯部的弧度是派,就是这一点。或者说这个项链我跟你演。这个我们再来理解一个非常普通的,好多人都不明白二的 i 次方是什么意思, 我们稍微的把它化点一下,我们知道 x 等于一的 nonax 方啊,这个可以说是一个比较无聊的变化,但是当涉及到负数平面的时候,经常会用到这个,比如说二的 x 方可以写成一的 诺奥迪 s 等于一个 i 乘以诺昂,他的意思就是弧度是诺昂,你 立了这些,最后我们再来说一下欧拉公式与三角函数之间的关系啊。刚刚我们开了展开的方法,探究了狂乱式的 加二乘三四的等于一的 ic 的时候,但是能不能用几何的方式去讨论他们的关系。可以啊, 这是一的 ict 代表的一个圆,加上这个一还是一个相反的啊,这是一的负 ic 大一,这个角度是 c 的,那么这个角度也是 c 的。这两个是一个 等腰的,那么画条线,那么这个肯定垂直的,这个长度是这个总长的一半,这个总长是多少呢? 是一的 ic 塔一减去一的负 ic 塔一啊,这两个项链先减了,再除以二,就是这个项链了,而这个项链是什么东西呢? 刚好是 a 乘以三西塔呀,所以三西塔等于一的 i c 塔一减去一的负 i, c 塔一 除以二来,同理啊,这个扩散式的是这两个项链相加的,形成这个项链的一半。 ok, 我理解了,从三角函数推欧拉公式,从欧拉公式推三角函数,我们再来理解最后一个公式,一的 ipad 十方加一等于零,实际上他只是欧拉公式的一个特质。 一的埃西塔四方等于矿山西塔加上埃及山西塔,当西塔等于 pass。 一个 i 派十分等于科三派加 i 等于十二派,这个刚好是等于零,这个刚好是等于负一。 一项意大利派次方加一等于零。他之所以如此的著名,是因为他把自然数,把圆周率派,把自然底数, 还把虚数给紧密的联合在一起了,而且还产生了一个神奇的结果,您有关于欧拉公司的另外一些奇特的应用,我会放在本视频的合集里面啊,感兴趣的可以去看一下。
7422火星课堂 05:32查看AI文稿AI文稿
05:32查看AI文稿AI文稿好,我们今天来看一下这样一道抢集奇,已知非零时数 x y 满足 x 三次方加 y 的 三次方加三倍 x 方 y 方等于 x 的 三次方加乘以 y 的 三次方, 则 x 分 之一加 y 分 之一的可能取值为多少?那么在讲这个式子之前,我们看到这有 x 三次方,这有个 y 的 三次方, 然后呢后面是 x 三次方乘以 y 的 三次方,那这个式子要应用的时候呢?有点像我们前段时间我们讲过的什么立方和立方差那个样子,对吧?但是他有一些不一样的地方。我们先讲一个公式,叫欧拉公式, 那欧拉公式是什么呢?欧拉公式的可能有一些同学都没有认识过啊,是 a 的 三次方加 b 的 三次方加 c 的 三次方减去 三 abc, 他 就等于谁呢?他就等于 a 加 b 加 c 去乘以 a 方加 b 方加 c 方减去 ab 减 ac, 再减 bc, 这就是我们这块所讲的欧拉公式。那么所对这个题目来说的话,我们先对等号两边同时除以 x 的 三次方, y 的 三次方,那第一个呢?就会变成这样, 这是第二部分加上第三部分,那么上下去除一个 x 方 y 方以后,他就是 x 乘 y 分 之三,那么右边是一个一,那么再进一步整理,那其实就是 y 的 三次方分之一,那就可以把它写成 y 分 之一的三次方,那这个的话呢,可以写成 x 分 之一的三次方 去加上他,那么就是把这个一移到左边来,变成这个减去一,对吧?或者说写成加上这个什么呢?负一的三次方,对吧?啊?加上负一的三次方,那你可以把它写成这个样子, 那么最后这块呢,把它就可以写成什么呢?减去三倍的它,那这位可是个加号,你看刚好正对的是我们的公式三,乘以 s 分 之一,乘以 y 分 之一,再乘一个负一, 那么结果等于什么呢?零,好,那我们这个呢,其实我们看到左边就是我们欧拉公式的左边部分,对不对?那他就应该等于谁呢?他就应该等于 a 加 b 加 c, 套公式啊,所以你看我们知道了这个公式以后呢,非常的好用,直接套公式就可以。 所以 s 分, s 方分之一加 y 方分之一,再加上这个负一的平方,就是加一, 再减去两个的乘积,那就是 s 分 之一乘以 y 分 之一,然后再减去 s 分 之乘负一,那就是加 s 分 之一,然后呢后面这个 y 分 之一乘以负一,那么就是加 y 分 之一,就会变账。 那么前面我们讲过,我们说后面遇到这种式子,对吧?这种式子的话,它可以看成三个数的什么呢?平方和的平均值,那么就是 a 加 b 的 平方,加上 a 加 c 啊,你像我们这个地方,其实就是 a 方, b 方 c 方,减去它和 a 减 b 的 平方,再加上 a 减 c 的 方,再加上 b 减 c 或者一个平方,三个完全平方式,再乘以二分之一就可以了,相当于是给这个式子呢,本身先乘二,再乘二分之一就会变账。变账以后呢,我们再进一步一个整理,就是 s 分 之一加 y 之一,再减去个一, 然后呢那么再乘以二分之一,乘以这个 s 分 之一,我们会发现这个地方是减,对吧?所以 s 方 y 方,然后呢我们就是减去 s 减 y 分 之一的平方,再加上 这个 y 分 之一,那后面就是 y 分 之一去加上一或的一个平方,然后后面这个地方呢,就是 s 分 之一去加上一或的一个平方,就会变这样,然后呢,我们把它分解成两个一式相乘了, 那么就是分别每一个音式就等于零,所以 x 分 之一加 y 分 之一减一等于零,或者剩下的部分为零,剩下部分为零的话,它出现了三个完全平方式,那么三个完全平方式之合是大于等于零的。要想结果为零,那就是每一项为零, 那就是 x 分 之一减去 y 分 之一要等于零, s 分 之一加一等于零,那 y 分 之一加一要等于零,所以我们从这里面知道, s 等于负一,那 y 等于负一, s 等于负一,往这边带的话,那就是负一,这个 y 分 之一结果也是负一,前面有一个减号,所以它结果就是零,满足这块的式子,对吧?那前面这块呢,是 x 分 之一加 y 分 之一,结果等于一,所以我们这一块呢,其实我们看到另外一个 x 等于负一了, y 等于负一了, s 分 之一加上 y 分 之一,结果就等于负二,所以我们这块看到一个答案,就是它可以 等于一,它也可以等于负二啊,所以这个题选它的可能取值是负二和一。
26玩转数学陈老师 08:54查看AI文稿AI文稿
08:54查看AI文稿AI文稿大家好,欢迎来到这里。在数学的世界里,有些方程它们怎么说呢,简直就是艺术品。而今天我们就要深入探索其中最著名的一个欧拉公式, 它把数学里最重要的五个常数都联系到了一起,听起来很神奇对吧?但它到底是怎么运作的呢? 好,这就是我们今天的寻宝图,你可以把它想象成一个侦探故事。我们一步步寻找线索,最终要解开一个核心的谜题,那就是一个指数上竟然带着一个虚数,最后怎么就能画出一个完美的圆呢?听起来是不是有点匪所思?我们这就出发。 行,那我们就这开始吧!第一步,咱们先来看看这个谜题本身到底长什么样 呐?就是它欧拉公式。我知道我知道,对,一眼看上去有点哎,吓人,但别担心,咱把它拆开看就明白了。你看右边有 cosine cda 和 sine cdo。 如果你还记得中学数学,这其实就是在一个圆上某个点的 x 坐标和 y 坐标嘛。 所以这个公式本质上只是用一种全新的看起来有点怪的方式来表示一个二维平面上的位置。 接下来就是见证奇迹的时刻了,当这个角度 theta 开始变化的时候,你猜 e 的 i theta 这个点会怎么样?是到处乱跳吗?不是的,它开始移动,然后描绘出了一个完美无瑕的圆。说真的,这难道不酷吗? 这就演出了我们最核心的问题,对吧?为什么啊?数字 e 就是 那个自然对数的底数,他跟圆跟旋转到底有什么关系?这俩东西听起来完全是两个世界的好吗?好,这就是我们今天要破解的谜题,那么是时候开始寻找线索了。 好的,我们的第一个线索就藏在一个你可能听过的概念里,变化,但不是普通的变化,而是瞬时变化,也就是在一个极小极小的瞬间,到底发生了什么? 怎么找到这个瞬时变化呢?其实很简单,想象一下,你先在一条曲线上随便找两个点,在它们之间画一条直线,没问题吧?好,现在让这两个点开始互相靠近,越来越近,无限的靠近, 会发生什么事?你画的那条线,它会停止摆动,最终变成在那个点上的一条完美的切线,而这条切线的斜率是多少? bingo, 那 就是倒数。 所以简单来说,导数是什么?它就是一个函数在任何一个点的精确变化速度,或者说就是它的斜率,你可以把它想象成是数学函数的速度。记 好了,来看第二条线索,这条线索的来源你绝对想不到,它来自一家银行,当然不是普通的银行,而是一家能解析数字 e 的 奥秘的神奇银行。 设定是这样的,这家银行给你一个难以置信的利率,每年一百拍,你存进去一块钱,一年后你就有了两块钱,很简单对吧?但好玩的地方来了,如果我们不等一年,而是更频繁的去结算利息,会怎么样呢? 比如说,我们一年算两次利息,过了半年,我们先结算百分之五十的利息,把利息加到本金里,然后让新的总额在下半年继续生息,到年底你就会得到两块两毛五。嘿,比刚才多了点。 好,我们再疯狂一点,一年算四次怎么样?每个季度都算一次,现在我们年底能拿到两块四毛四啊,你发现什么了吗?钱虽然还在变多,但是每次多出来的那个增量他在变小,这个增长的幅度变缓了。 那终极问题来了,如果我们不是每天每秒,而是计算复利会怎么样? 你可能会觉得钱会涨到无限多,但实际上并不会,他会触及一个上限,无限的逼近。一个非常特殊、非常具体的数字,这个数字就是 e, 大 约是二点七幺八二八。 好,这个故事很酷,但它真正的意义是什么?这种连续的、每时每刻都在增长的模式,对于数字 e 的 本质到底意味着什么呢? 这句话就是关键。在连续增长的情况下,任何一个瞬间,你账户里钱增长的速度都和你那个瞬间账户里的总量是完全相等的,你的规模决定了你的增长率。 现在咱们把线索串起来了,还记得第一条线索导数吗?它衡量的是变化率。我们刚从神气银行那学到了什么? 增长率等于当前的总量,所以我们在寻找一个函数,它的导数就是它自己。在整个数学世界里,只有一个函数拥有这个超能力,那就是 e 的 x, 这就是它的定义属性 e 的 x, 这个函数的增长率永远等于它当前的值,这就是 e 的 精髓。 好了,关键时刻到了,我们把所有线索都摆在桌上,一边是我们的第一条线索导数,它告诉我们关于变化的一切。另一边是第二条线索数字 e, 一个为自我增长而生的数。现在我们引入最后一块拼图,虚数单位 i, 当这三者相遇时会发生什么呢? 谜底就要揭晓了。注意看,函数 e、 x 的 天性就是增长,它的导数是它自己,意思就是它会沿着自己当前指向的方向增长,你可以把它想象成一个一直往前冲的火箭, 但是现在我们在指数上加了一个 i, 在 负平面上乘以 i 意味着什么?意味着旋转九十度。所以现在指令不再是向前冲了,而是变成了朝着与你当前位置乘九十度角的方向增长。 你仔细想一下这个画面,你站在一个点上,你下一步的方向永远和你当前的位置垂直,这会走出一条什么样的路径?一条完美的圆,它只能画出一个圆。而这朋友们就是为什么正弦和余弦函数会出现在这里,因为它们就是描述圆周运动的数学预言。 所以你明白了吧?谜题解开了,欧拉公式根本不是什么巧合,它是 e 和 i 这两个基本概念相遇后,一个美丽又合乎逻辑的必然结果。 e 提供了持续增长的引擎,而 i 则负责把这种增长掰弯,变成了一个完美的圆周运动。 好的,最后我们来思考一个问题,刚才这趟奇妙的旅程之所以能够成型,是因为我们愿意接受一个所谓的虚数的存在。这会让你想,对吧?数学是不是一个我们可以随便制定规则的游戏? 如果我们能发明负一的平方根,那为什么我们不能?呃,比如说定义一下除以零等于多少呢? 咱们试试看会发生什么?假设我们就这么规定,一除以零等于某个数,叫它 z 兄吧。这就意味着 z 乘以零必须等于一。好,现在我们把等式两边都乘以任意一个数,比如 x, 稍微整理一下,你就会发现 z 乘以零等于 x。 但等一下,我们一开始就说了, z 乘以零等于一。如果这两句话都对,那就意味着 x 等于一, 可 x 是 任意一个数啊。这就意味着五等于一,一百等于一,圆周率也等于一。整个数学体系就崩塌了,它完全说不通了。 这就是最关键的区别。当我们定义 i, 也就是负一的平方根时,我们没有破坏数学,我们扩展了它,我们把一维的数轴打开,成了一个美丽的二维平面,它创造了新的可能性和新的工具。但是尝试去定义除以零呢? 他什么也创造得了,反而会摧毁一切,他会把整个丰富多彩的数字世界贪缩成一个所有数字都毫无区别的没有意义的点。一个是创造,一个是毁灭。 那么这就给我们留下了一个很深刻的问题,去思考数学究竟是我们发现的,就像发现宇宙隐藏的规律一样,还是我们发明的一套只要不自相矛盾就足够优美和强大的游戏规则? 欧拉公式的故事似乎告诉我们,它可能两者兼有,而这个想法,嗯,它本身几乎和欧拉公式一样优美。
13光锥启示录 05:31查看AI文稿AI文稿
05:31查看AI文稿AI文稿各位,这道题啊,非常的有意思啊,非常的烧脑,为什么有意思?我们来看一下啊,说已知 x 六次方,减 x 五次方,加 x 四次方,减 x 立方,加 x 平方,减 x 加一等于零,求 x 的 七次方。那有的同学说了啊, 很简单吗?左边进行生次对不对?我左边都乘上一个,什么乘上一个 x, 这边不是变成七次了吗?我们求的就是七次,生次之后之后能得到什么呢? x 七次方对不对?减 x 的 六次方 加 x 的 五次方都生一次吗?减 x 四次方,再加 x 立方, 再减 x 平方,再加 x 等于零,对不对?左右都乘上 x, 我 们求的是 x 七次方,大家有没有观察出来,这个负六 r 负六,呃,不是负的, x 六次方加 x 五次方和这个你看到没有? 正好互为什么相反数呀?各位,这个和这个是不是互为相反数?正好都是 r 相反的, 这样的话,上面这个加下边这个是不是直接变成 x 七次方加一等于零了呀?这一步能不能看明白? 就这么一大坨和这个是相反数。所以说 x 七次方肯定等于负一啊。到这一步,各位,有的同学说了, x 七次方等于负一,我能不能推出来 x 等于 负一,带回去,你试一下行不行? x 等于负一,负一带进去一, 这变成加一,变成二了,这是一,这也是一,一这也是一啊,不成立啊。有同学说了, x 等于负一不成立啊。那 x 等于七,不是 x 七怎么等于负一?他成立不成立?各位,他是成立的, 为什么成立?因为这个七字啊,是有七个根。各位,七个根,这个六次的是六个根, 这为什么会多一个根呢?多了一个 x 等于负一,这个增根它是增根,也就是说还有六个根隐藏起来了。 x 七次方确实等于负一,它等于负一,那六个根在哪?今天给大家说一下啊!这六个根 我给大家列出来啊,这牵扯到大学里边数学了啊,下面比较高能啊,请谨慎观看啊。那六个根在哪?就说 x 七次方等于负一啊,他的其他的根在哪?我给大家一一列出来啊。第一个根是一旦 七分之一派二,这个二是虚数啊,二是虚数,还有一个是还有一个跟什么呢?七分之三派二,还有个什么一的七分之五 派二,还有个什么一的七分之九派二,还有个什么一的七分之二十一派二 几个了?一二三四五六,还有一个啊, e 的 七分之十三拍啊,哎,这七个根怎么这么奇怪?看着大家有没有发现一个问题,这个第四个根啊, 第四个根是不就是 e 的 派 i 次方呀? e 的 派 i 次方,各位,不就等于负一吗?这不欧拉公式吗? e 的 ip 次方等于负一, 这个增根就是他,其实他不应该是这个,他不是这个方程的根,但是这六个根,各位,剩余这六个根是这个方程的根,不相信大家可以验证一下啊。怎么验证?你看啊,第一个根对他进行七次方, 你看他的七次方,那不就等于负一吗?对他进行七次方,各位, 那是多少?一的三派 i 次方,三派 i 次方也是负一,这是多少?五派 i 一 的五派 i 次方也是负一。那个同学问,为什么 派 i 和三派 i, 五派 i 还有什么七派九派十一派,相差了两个派,两个派为一圈, 这个道理能没明白?我给大家练这个画一个极坐标系啊,大家能不能听懂啊?听不懂我也没办法呀,这是大学里边数学,听个大概就行啊。但是咱俩人思维加上这是个极坐标轴啊,这边是负,这边是一,这边是负一啊, 这个一呢?它是多少呢?一的零次方。各位,这个负一呢?是一的派二次方, 他从这转半圈,转半圈是一个派,他就变成负一了,那再转半圈呢?变成两派了,两派二就变成一了, 那三派二呢?你看又转了半圈,一的三派二呢?三派二也是负一,又转一圈呢?一的四派二,四派二就变成正一了,这个五派呢?五派二呢? 他又变成负一了啊,他就这样转来转去的。所以说这个啊,大家能不能明白?所以说他相差两个派,你看一个派,三个派,五个派,还有七个派啊,回头大家自己再好好演算一下,讲不明白了,各位。
5746马老师数学课堂 06:51查看AI文稿AI文稿
06:51查看AI文稿AI文稿维勒斯 formula 是 一座桥梁,连接了指数 exponients、 三角 trigonometry、 负数 complex number、 几何 geometry、 微分方程, differential equations 和物理世界的振动 isolation 与相位 phase weyls formula 真正做的事情是把 geometry 变成 algebra, 把周期变成指数,把旋转变成乘法,把微分方程呈现行化。它是 complex analysis 的 起点, fourier analysis 的 核心, quantum mechanics 的 语言以及工程与物理的通用工具。 例如,量子系统的动力学本质上被编码为负平面上的旋转,而这种旋转由负指数 complex exponential 表示。 weelys 封面了,也是负分析 complex analysis 结构的基石。它连接了 power series 密集数解析函数 analytical functions, culture raymon 方程以及流数定律 recipe theorem。 它是负指数函数周期性和负对数多值性的根源。 本视频将讲解证明 weelsc formula 的 三种方法作为本频道深入学习 complex number 和 complex analysis 的 基础。当然,推到 weelsc formula 的 方式取决于你如何定义 exponential function。 最常见的定义是密集数 pair series。 用这种方式来定义 exponential function 也是证明该公式最经典的方法。我们把 pair series 中的奇数项和偶数项分开,然后利用定义 i 平方等于负一对每一个括号内的表达式稍作改写。 接着我们就能识别出第一个极数对应的是 cosine theta, 第二个极数对应的是 sine theta, 于是就得到一次的 i theta 等于 cosine theta, 加上 i 乘以 sine theta。 但这个证明并不是特别有启发性,因为问题在于,为什么这些极数会对应正弦和余弦函数呢?为了解决这个问题,人们通常干脆直接用这些极数来定义正弦和余弦函数。 从严格意义上说,这样做并没有问题。但这些级数究竟是如何与正弦、余弦的几何特征联系起来的呢?我们在以后的视频中来专门探讨这个问题。 现在来看 x potential function 的 第二种定义。这种定义利用了它与微分 differentiation 有 关的性质,也就是说,它的 derivative 就是 它本身乘以爱。正是这一性质构成了一个非常漂亮的格式化证明。 在解释这个证明之前,我们需要一个小事实,也就是 complex number 如何与 i 相乘。当 a 乘以 i 时,不出意料地得到 a i, 而当 b i 乘以 i 时,会得到 negative b, 因为 i 的 平方等于负一。这意味着点 a b 乘以 i 之后,被应射到点负 b a。 不 过,这里有一个非常直观的几何解释, 这是点 a b 乘以 i 之后,我们会得到这里的点负 b a。 如果把向量和角度一起画出来,就会更清楚地看到与 i 相乘到底做了什么。没错,它就是绕圆点逆时针旋转一个直角。因此,我们可以进入正式的证明了。 首先,我们需要理解这个导数究竟意味着什么。 et 的 i theta 可以 被看作是在 complex plane 上的位置,但这个位置会随着 theta 的 变化而变化,因此,这些变化的位置形成了一条轨迹。 在这里,这条轨迹并不是随机的,而是由这个导数方程所控制,左边表示沿着轨迹运动的粒子的速度, 右边则是将未知向量绕圆点逆时针旋转一个直角后的结果。这种关系再加上,当 f theta 等于零时,指数函数的值是一,这两个事实共同决定了这条轨迹。 于是我们画出 complex plane。 当 f theta 等于零时,值是一,所以粒子从这里出发。 由于速度向量 velocity vector 始终与未知向量 position vector 垂直,因此促使速度 initial velocity 指向正上方。但是在极短的时间之后, velocity vector 就 不再完全指向正上方了,因为此时 position vector 已经不再是完全水平的。 事实上,随着时间的推移,这条轨迹恰好是一条单位圆 unit circle。 在 整个运动过程中, position vector 的 长度始终为一,因此速度的大小也始终为一。因为速度只是对 position vector 做旋转而没有任何拉伸。 于是在经过时间菲塔之后,运动的路程正好是菲塔。根据弧度 radian 的 定义,这一点的俯角 argument 恰好就是菲塔。 由于这个点是一次的 i feta, 我 们最终得到一次的 i feta 等于 cosine feta, 加上 i 乘以三 feta, 这就是微了四伏米了。 这个精彩的证明被 fable one brown 频道所采纳改编。现在来看一个特殊情况,当菲特等于派时,有扣三派等于负一以及三派等于零,因此一次的 ipad 等于负一。这通常被称为为了死 identity 欧拉横等式, 它常被认为是最美的公式。第三种证明,基于极限的定义。从 exponants 的 极限定义出发,我们来直观地看看这个极限定义是如何运作的。 首先,我们确定一和一加 i f t 除以 n 所在的位置,这里我们暂时取 n 等于二。然后,我们以零一和一加 i f t 除二为顶点构造一个三角形,并像之前展示的那样对这个三角形进行旋转和拉伸,从而得到它的平方。 但这只是 n 等于二十的情况,我们应该增大 n 的 值。这些三角形组合在一起会逐渐形成一个扇形。那么该如何解释这一现象呢? 在画出所有三角形之前,我们先关注图像中非常微小的一部分。我们在图中加入单位圆的一小段。虽然这个点并不完全在圆上,但随着 n 的 增大,它会越来越接近圆。 由于这里的距离是 f 除以 n, 根据 radian 弧度的定义,对应的圆心角也正是 f 除以 n。 因此,我们可以说在极限意义下,它近似等于 cosinefeta over n plus i times sine feta over n。 现在, e t 的 i feta 作为一加 i feta 除以 n 的 n。 次密的极限可以写成这样的形式, 根据 the mother's theorem, 角度会被乘上 n, 因此极限就是 cosine feta 加 i 乘 sine feta 再次得到。为了 si formula。
127Wondererus 03:04查看AI文稿AI文稿
03:04查看AI文稿AI文稿欧拉公式真的很美吗?反正欧拉本人肯定不知道,因为他从来都没写过这个式子。这是我们现在看到最网红的欧拉横等式形式,哎,确实好看哈。零一一派 i 对应了五个数学当中最常用的常数,用的运算最好也是加法、乘法和密。 目前数学公式搞选秀,好多大神都选择 c 位出道。不过数学毕竟不是比美,欧拉自己在论文里边从来没有写过这样的形式,而是会写成一个三角函数形式的横等式。这就我们邀请他老人家亲自来解释一下。这个公式的精髓在于,从这个等式展示了虚率数是如何被表示成实三角函数的。 我们沿着还有两个线索往前走,第一个叫虚对数,第二个叫三角函数。首先,虚对数这第一个线索呢?欧达得感恩他生活在一个好时代呀,当时虚数大论战已经过了气,所以遇事不就加个 i 玩,不仅不会被视为离经叛道,甚至还有点小时髦。我这视频啊,要是搁当年,那求赞求评论,那都得求挨个比方说这里欧达的一封信就提到,跟他亦师亦友的 约翰不努力,早就发现了一个圆的扇形,居然可以用虚对数来表示这一约翰大兄弟莫非才是真正的发明人?可惜他自己后面写的文章漏气了,他非得说 low 负 x 永远等于 low x, 并且坚持说 low 负一就等于零。哎,这个对负对数的理解啊,还是太浅了,甚至跟他自己之前的结论矛盾。不过 同时也确实给了欧拉很多灵感,他意识到啊,曾经仅仅是用来解三四方程的虚数,实际上可以在真实的扇形当中出现。 第二个线索是三角函数。这回咱又得聊聊牛顿了,因为三角函数此前的发展恰好是牛顿的三个好朋友一起推动的,他们是哈雷克特斯跟蒂莫夫。这个也很好理解吧,当年去做三角学应用的就是以天文为核心的物理学, 牛顿是这方面的行家呀。科特斯之前算天体物理的时候,琢磨着怎么算这个妥球的鞋面,结果一不小心摸到了这个公式的边后面丁默福沿着好哥们的路再往前走一步,他发现啊,这个里边的形式很有意思,这里也是个虚数,那假如把他自己称上自己一下,稍微换点之后就能发现他居然是 q 赛 r x 加上 i 倍的 c r x, 这就有意思啦,还可以接着再乘。最后蒂莫夫得出结论,这 q c x 加上 i 倍的 c x 的 n 次方,结果就是 q c n x 加上 i 倍的 c n x, 这就是传说中的蒂莫夫公式了,到此为止都没欧拉啥事。所以最后肯定是欧拉把所有理论给大一统,成就无敌的欧拉公式了吧。结果当然也不是 各路科普大神把欧拉红等式的几何意义演绎的美轮美奂,在欧拉本人证明的时候,真的就是直接拿泰勒展开给正的,也是丢一个学过数学的现代人过去看欧拉正这个,那真是吐槽停不下来。 首先他把一的 x 方的无穷极数直接带进去个 ix, 严格来说吧,这很不严格,这复变还说性质都还没研究呢,你下带再出问题可怎么整啊?接着他把这个无穷极数的顺序轻轻一调,哎,大家千万别跟他学,要知道这极速下改顺序甚至有可能影响到收敛和发散的性质,这个涉及到篱笆重排定理,跟条件时候两个绝对收敛之类的有关。总之,欧拉就这么非常不严, 紧紧的把结论给推了出来,完全没有我们想象中的轻松写意,而够像是一个莽撞鬼。这么看,欧拉好像没有传说中的那么神呢。没错,欧拉确实不是爽文男主。数理科学从来不是没头没脑,天降猛男就能拯救世界的,但欧拉在科学家里面 绝对是最有灵感且最勤奋的代表。至于 ol 公式到底是不是史上最美最神秘的公式,我只能说这个公式的真正伟大之处 就是结识了虚顿术跟三角海柱之间有根本的关系,这虚实之间的深刻联系将陆续由达朗、贝尔、拉格、朗日跟柯西给完善。总之,别管一个公式长得有多好看,比形式更美妙的,永远是对他背后真理的探索呀!
8480王耀绅 02:12查看AI文稿AI文稿
02:12查看AI文稿AI文稿两分钟彻底搞懂拉格朗日,求极限!首先看看这道题你会用什么方法做好?同学们,我们来看一下这道题目啊。首先这道题目其实方法是有很多的,但是我觉得最快的方法就是用拉格朗日去做啊,什么时候会想到用拉格朗日呢? 当你极限中啊,发现函数名相同的两个函数相减的时候,我们就要用到这个拉格朗日。拉格朗日的公式我已经写到上面了啊, f a 减 f b 等于 f 克 c, 撇乘上 a 减 b, 这个克 c, 它是介于 a 到 b 之间的一个数啊,主要是由于我们不知道 a 和 b 谁大谁小啊,反正就是克 c 在 两者之间嘛,对不对?嗯, 那么接下来呢,我们第一步先呢啊,根据这个公式咱们套一下好,套完之后我们是不是应该变成这个样子啊?扩散的导数是不是复散啊?那是不是直接写成复散克 c 啊?然后里面变量值相减,跟这个公式一样,是不是写成 x 减三 x 啊? 那 x 减三 x 呢?这个公式大家必须要记住啊,当 x 趋近零的时候,它减它啊,之间等价于六分之一, x 三次啊,所以说我们先进行不等价, ok, 等加完了之后呢啊,我们上面这个 x 三次和 x 四次是不可以约分一下好,整理完之后,我们是不是得到了下面这个极限,我们把常数提到外面嘛,对不对?那最终的问题就聚焦在 这个函数的极限到底是多少呢啊,我们根据那个公式啊,知道可 c 它是介于 a 到 b 之间的,那我们这道题 a 和 b 是 不是 x 和三 x 啊?所以说这个可 c 它应该是介于 x 与三 x 之间,对吧?那么接下来重点来了,我们一道题到底能不能用拉格朗去算?那其实本质上你要根据夹逼定律去判断一下两侧的极限到底是否一致啊?为什么要这么去想呢? 因为你看我这个刻 c 啊,它是处于 x 和三 x 之间,那我们这个函数的极限是不是应该夹于这个极限和这个极限之间啊?我们接下来去算一下这两边的极限是否相同啊?这两个极限应该很简单,是不是应该都是一啊?所以说两侧的极限是不是刚好相同啊? 那我们最终呢,由加倍定律可得,我们这个目标函数的极限是不是也是一啊?因此它的极限是一啊。我们最后答案呢,是不是就是负六分之一?你做对了吗?
6542小魏老师讲高数







