板块问题共速之后怎么分析
粉丝1.0万获赞2.1万
相关视频
 07:07
07:07 13:14
13:14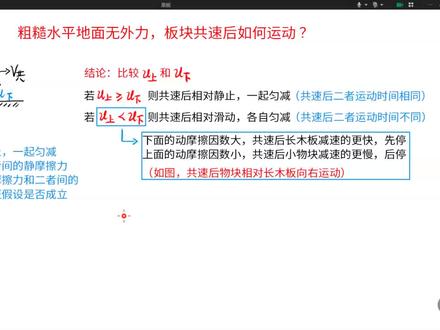 07:28查看AI文稿AI文稿
07:28查看AI文稿AI文稿哈喽,同学们大家好,我是物理祥老师,今天要跟同学们探讨的是粗糙水平地面无外力板块供塑后如何运动。没错,我们今天要探讨的不是物块与长木板是怎么供塑的,而是探讨板块供塑后如何运动。 如果地面是光滑的,我相信同学们都知道,板块供塑后会相对静止,在光滑的水平地面上一起做匀速直线运动。可如果地面是粗糙的呢?板块供塑后如何运动?同学们,你们是怎么认为的呢? 此时啊,很多同学会想当然的认为,既然地面是粗糙的,那么板块供速后一定是相对静止,一起做云减速直线运动,直到停下来。其实不然, 这里我们先讲结论,一会再来带同学们证明这个结论。板块共诉后,我们应该比较缪上和缪下, 谬上是二者之间的动摩擦因素,谬下是长木板与地面之间的动摩擦因素。板块供述后,我们应该先比较谬上和谬下。若谬上大于等于谬下, 则供速后二者相对静止,一起做云减速直线运动,那也就意味着供速之后二者的运动时间相同。 若没有上小于没有下,则供速后二者会相对滑动,各自做云减速直线运动,那也就意味着供速后二者运动时间不同。这里啊,同学们可以这样记,下面的动摩擦因数大, 所以供速后长木板减速的更快,他会先停。上面的动摩擦因数小,所以供速后物块减速的更慢,他会后停。既然供速后物块减速的更慢,那就意味着供速之后物块跑的更快。所以如图所示, 共塑后五块相对长木板向右运动,同学们,你们听懂了吗? 我们接下来啊,来证明一下这个结论,我们用假设法来证明,我们一起来看一下证明思路。我们假设共诉后,二者相对静止,一起做云减速直线运动, 我们就可以先对整体受力分析列牛顿第二定律,求出共同的加速度,再隔离小物块,对物块单独受力分析列 牛顿第二定律,求出二者之间的净摩擦力。我们用假设前提下求出的净摩擦力与二者之间的最大净摩擦力去比较,来验证假设是否成立。 如果在假设前提下求出来的净摩擦力大于二者之间的最大净摩擦力,你不觉得很离谱吗?那就说明啊,假设不合理,假设不成立。如果你在假设前提下求出来的净摩擦力, 二者间的静摩擦力小于等于二者间的最大静摩擦力,说明你的假设是合理的,则假设成立。好了,在证明之前啊,我们先对物块和整体受力分析。 板块共诉后,我们先受力分析。由于地面是粗糙的,所以地面会阻碍长木板,地面会给长木板一个向左的摩摩擦力啊,这个摩擦力是滑动,摩擦力是地面给长木板的。 那共塑之后,地面阻碍长木板,那长木板是不是得拉一个垫背的呀?所以他也会去阻碍小雾块,那长木板给雾块的摩擦力是向左的, 因为我们假设二者相对静止,所以二者之间的摩擦力是静摩擦力,我们用 f 静来表示。根据牛顿第三定律,力的作用是相互的,你给我一个向左的静 摩擦力,那我当然也得给你一个向右的静摩擦力了。二者大小相等,方向相反, f 静就等于 f 静一撇, 那 f d 呢,是滑动摩擦力,我们可以把它表示成缪下啊,小 m 加大 m 乘以几,那二者之间的最大径摩擦呢? 啊,就等于二者之间的滑动摩擦,就等于没有上小 m g。 好了,准备工作我们已经做完了,那么我们就可以先对整体受力分析列牛顿第二定律。 对整体受力分析时,同学们要注意,我们只考虑外力,不考虑内部的力,二者之间的 力属于内力。那这个整体啊,受三个力总的重力,地面给的支持力,还有地面给的向左的摩擦力。对整体受力分析列牛顿第二定律。 这个地方我们得用整体的质量,我们就可以求出二者共同的加速度了。 接下来啊,我们再单独隔离小物块受力分析练牛顿第二定律, 我们就可以把这个静摩擦力给他求出来了,我们将共同的加速度带入啊,那我们就可以解得 f 静啊,就等于缪下小 mg。 那怎么验证假设是否成立呢?我们要拿假设前提下求出来的二者间等 静摩擦力与二者间的最大静摩擦力,就和这个啊去比较弱。假设前提下求出来的静摩擦力就是这个缪下 m g, 他小于等于二者间的最大静摩擦力, 即缪下,小于等于缪上,则假设成立,那就意味着共诉后,二者会相对静止,一起做云减速直线运动。 若我们在假设前提下求出来的二者间的净摩擦力大于 大于二者间的最大径摩擦力 没有下,大于没有上,则假设不成立,那就意味着共诉后二者会相对滑动,各自做云减速,直线运动。 好了,那这个问题啊,就给同学们讲到这里,我希望同学们能够在理解的基础上,能够在会证明的基础上啊,要熟悉这个结论,那以后再碰到类似的情景,我们就可以轻松的迎刃而解了。 关注蒋老师,你搞不懂的知识点,你容易丢分的易错点,你需要加强的重难点,都在这里,同学你不关注一下吗?
346金牌物理蒋老师 10:22查看AI文稿AI文稿
10:22查看AI文稿AI文稿朋友们好,我是邢科一高中李慧老师。今天我们来看一道关于板块的应用题。首先我们来简单读一下题,要说如图所示, ab 质量均为一千克, ab 之间和 b 与地面之间的动量关系数都告诉你了,一个是零点五,一个是零点二。刚开始, a 静止在 b 左端, b 停在水平地面上,某时刻起给 a 施加一个 大小为九牛的拉力, f 一 秒以后撤去 f, 最终 a 恰好停在 b 的 右端。啊,那我们看到这是一个重要的临界条件,我们之后可能要用到 a 恰好停在 b 的 右端啊,挂在这。然后我们来看题,第一问,他说通过计算说明前一秒内木板 b 是 否运动好,我想考虑木板 b 的 运动状况,是不是得对 b 进行受力分析啊? 好,那我们要想啊, a 和 b 之间,它到底是近摩擦还是远摩擦呢? 好,那这是不是一个关于相对滑动零件的问题?关于相对滑动零件,我们怎么求的? 对了啊,就是球相对滑动的那个瞬间,那时候我们的拉力是多少?那我们的做法应该是对了,此刻 a、 b 之间的摩擦力应该恰好为滑动摩擦力,也就是最大劲摩擦, 然后进行整体隔离啊,或者说隔离 a 隔离 b 列两个牛顿第二定律公式就可以把大 f 解出来了吧。好,那我们可以先整体后隔离,假如整体法,整体法,那把 a、 b 看做一个整体,它们的受力是怎么样呢?受到一个外力 f, 还有一个地面的摩擦力。 来,我们来写一下, f 零减去 f 地面的滑动摩擦力就等于二 m a。 接下来可以隔离 a 或者 b 都可以啊,那我们在这可以就先隔离 a 吧, f 零减去 a b 之间的滑动摩擦力啊。 f a b 等于 m a。 好,通解方程啊,我们可以求出 f 零等于六纽, a 等于一厘米二次方秒。 ok, 好, 又因为我施加的力 f 是 大于 f 零的,所以 ab 有 没有相对滑动?哎,对了,所以 ab 产生了相对滑动。 产生相对滑动以后,我们对于 b 进行受力分析就好分析了吧, b 受到什么力?那我们在这里画一下, b 受到一个来自 a 的 摩擦力,方向向右大小呢?大小?其实刚刚我们在这的时候就应该把 a b 摩擦力表示出来了。 of a b 应该是等于五牛, 地面滑动摩擦力也是在第一步的时候就给它求出来了,地面摩滑动摩擦力应该是等于四牛,你会发现,哎,这个 f a d 是 大于滑动摩擦力的,大于地面的滑动摩擦力,那所以 a 能够带着 b 一 起跑,对不对?我们说了,那谁的最大劲摩擦力越大,那么 b 就 跟着谁跑,所以 b 应该是可以运动的。 然后看第二个角,求一秒末物块 a 的 速度,那我们想求它的速度,是不是要对它进行受力分析?对 a 来说,它受到一个拉力,还受到一个 a b 之间的摩擦力。 我们来求一下, f 减 f a b 就 等于 m a。 好, 我们求出来,这个 a 应该是等于 四米每二次方秒,所以 v a 就 等于 a e 乘以时间 t 等于四米每秒。 好,没问题,我看第三问,它让你求木板 b 的 长度,那求木板 b 的 长度要看哪个 条件呀?对了,这块长度是跟运动学有关的,那我们肯定要去找重要的零件,也就是这个最后一句话,最终 a 恰好停在 b 端,那同学们想, a 恰好停在 b 端, a 的 速度就是一定是为零吗? 不一定啊,他恰好停在 b 的 右端,这个零件应该是 a 和 b 共速的时候 啊, a 和 b 共速时, a 就 一直在 b 的 最右端。抓住这个以后,我们来去想一想 啊,共速,那我肯定要把 a 和 b 的 速度都给表示出来,并且 a 恰好停在 b 的 右端。那我们来画一画,刚开始从这走了一段时间后, a 在 b 的 右端, 你会发现 a 和 b 它们俩的位是不是有一些关系啊?啊,假如 a 啊,我就看它最左侧,它的位是这块 b 呢?哎,从这到这 x a 和 x b 有 什么关系啊?对了,它们有一个数量关系,就是 x a 减 x b 等于 l, 这个 l 就是 木板的长度。好,我已经找到我要求的东西了,那把我刚刚说的第二个零件点也给它放在上面,就是 ab 共速, ab 共速 a, a 就 等于 ab。 好, 接下来我们想办法去表示这两个零件。 我们先看这第二个理念,因为有了速度以后,你更容易去找我的胃液哦, v a 等于 v b, 那 我想啊,刚开始 a 是 一个什么样的运动? 刚开始由于我有一个 y f, 所以 a 是 一个匀加速直线运动,并且在第二题里面第二小问里面我们已经求出来了,在前一秒钟内,我匀加速直线运动的加速度是二, 结束这个一秒的那瞬间, va 的 速度是四米每秒。那我们讲,等我把这个 f 给撤去以后,撤去 f 后, a 的 运动状态是不是要改变?对啊,那现在 a 它应该做什么运动?撤去 f 后, a 应该是,哎,对,零减速。零减速。那加速度如何?求加速等于 mu a m g 除以 m 等于 五米,每二次方秒,它是一个减速,零减速写在旁边,不然等会忘了出速度为多少。出速度为四米每秒。我们可以假设 呃到 a 达到 b 右端,一共运动了 t 秒, 然后我想办法表示一下运动 t 秒以后,我的末速度应该是多少?那末速度其实你可以只看第二段运动啊。只看撤去 f 后, a 它是一个匀减数,它是一个初速度为四的匀减数。好,嗯,那 撤去 f 后,它的运动时间我是不是直接用 t 减一能够表示啊?好,那 v a 就 等于 用 v a 减去 a 乘以 t 减一,因为我们只要看第二段的时间就可以了。放上去应该是等于四减去五乘以 t 减一。好, v a 表示出来,再看 v b, v b 在 f 撤去前和撤去后,它的运动情况一不一样。 当我有 f 的 时候, b 受到来自 a 的 向右的摩擦力, f a 对 b 还受到一个地面的滑动摩擦。那等把 f 撤去后呢?由于 a 它速度更快,所以 b 还要受到来自 a 的 一个滑动摩擦力,那同时地面的摩擦力是不是也不变?所以不管是撤去前还是撤去后, b 的 运动状态一直是处于一个哎,零加速直线运动状态。 a b 可以 算出来是等于和之前一样啊。 f d 除以 m, b 等于一米,每二次方秒, 那 v b 它就更好求了,因为它全程运动状态都是一样的,等于 a, b 乘以左右时间, t 等于 p。 好, 这两个我们求出来之后,它们相等就可以了,但是我们还缺一个求缺位移的关系。好,那,那我先把 a 的 等位移给表示出来, 把 a 的 运动分成两部分,第一个是一个匀加速,第二个是一个匀减速啊,把它两段分别求,那先求匀减匀减速, 然后我们让一二连立,一等于二,一等于二,所以我们能解出一个 t, t 解出来应该是等于一点五秒。好,从刚开始状态到末状态,但总运动时间是一点五秒。然后我们来表示谓语,是不是好表示啊?首先我们来算 a 的 谓语, a 的 谓语它分成两部分,一个是匀加速,一秒钟时间为 的谓语应该是二分之一, a 乘以一的平方,再加上后面匀减数,匀减数多长时间?就是一点五减一嘛,也就是零点五。好,再加上四乘零点五减去二分之一乘以 a。 撇,把这个标一下啊,这是第二 个运动过程的加速度, a 撇乘以零点五的平方。好,求出来就等于四减八分之五了, x b 更好求吧。应该是用二分之一 a, b 乘以一点五的平方,最后等于八分之九, double l 就 等于 x, a 减去 x, b 等于四分之九。 好,那这一题呢?一二小问比较简单,那主要是对 a b 之间是否相对滑动这个临界进行一个把握。第三小问需要用到最终, a 恰好停在 b 的 右端这个临界条件,这个临界条件告诉我们是 a b 共速的时候, x a 减 x b 等于大于 l 啊。首先我们去解这个速度方程,要注意 a 的 运动状态分成两部分,第一个是匀加速,第二个是匀减速的部分。
猜你喜欢
- 2967小八阿














