粉丝6903获赞3.0万
相关视频
 01:37查看AI文稿AI文稿
01:37查看AI文稿AI文稿你敢相信吗?一个简单的三门问题,百分之九十九的人都会输。假如你参加一档综艺节目,摆在你前面有三扇门,其中一扇门的后面有一根金条,如果你选中金条的那扇门,那么黄金直接送给你。首先你选择了一号门,此时主持人突然打开三号门,这是一扇空门, 紧接着他问你要不要换成二号门,请问如何做出对优决策?你会觉得每一扇门的后面都有可能是黄金,概率是一样的。大部分人也是这么想的,对,他们会坚定且自信的选择不换门。但真相往往恰好相反,如果坚持不换门,从三扇门里面选择金条的中奖概率是三分之一。 如果我们始终选择换门,那么它有两种情况。第一个,我们一开始选择了一扇空门,此时主持人会打开三号空门,我们知道二号一定带有金条,我们换门之后就会成功拿到金条。也就是说,刚开始我只要选中了空门,就一定可以中奖。第二种情况,我们一开始就选择了带有金条的这一扇门, 此时主持人打开三号空门,我们知道二号门一定也是空的,换门之后,我们会失去原有的金条。也就是说,如果我们刚开始就选中了带有金条的门,最终我们就会不中奖。 有可能会说,亮亮,你这要么中奖,要么不中奖,换与不换好像没有什么区别。如果我们坚持换门,你只要一开始选到了空门,我们就一定可以中奖,而你要知道空门有两扇, 因此我们选到空门,也就是中奖的概率是三分之二,而我们一开始选到金条反倒不中奖的概率是三分之一。也就是说如果你坚持不换门,我们中奖概率是三分之一。而如果你选择换门,我们最终中奖的概率是三分之二。所以当主持人问你是否换门的时候,我们一定要选择换,跟着亮亮无脑学习。
1451亮亮巧解数学 01:03
01:03 01:56
01:56 01:54查看AI文稿AI文稿
01:54查看AI文稿AI文稿用拍摄模拟三门问题,到底要不要改变选择呢?保证杠的人特别多啊!说是有三个长得一样的金蛋,只有一个有奖品,你先随机选择了一个,这个时候主持人会在你没有选的两个蛋当中用锤子敲碎一个没有奖品的 第一次机会,你可以换掉手中的,但选主持人没有敲碎的那个,请问你应不应该换?但是呢,这里有一个至关重要的条件,就是主持人是明确知道哪个带有奖品,主持人一定会敲掉一个没有奖品的,空弹给你五秒钟啊五,你 答案是应该换。哎,没想到吧,大部分人肯定觉得自己的蛋和主持人没有敲的蛋其中一个有奖啊,概率是百分之五十,换和不换有什么区别呢?这里我提供一种思维啊,当你选择了一个蛋的时候,你中奖的概率是三分之一,也就是另外两个没有被选的蛋。看了闫博君老师的讲解,我们用计算机来模拟一下吧, 来模拟十次不改变选择吧,每次只选第一扇门,然后不改变选择, 一看起来 夫多甚少。 再来模拟十次,还是先选第一扇门,但是改变选择 哈,这次看起来胜率很大了,但是实验次数还是太少。我们用拍照代码来模拟一百万次, 给大家看一下代码为了简化计算,另三号门总是大奖,而选手并不知道每次都是随机选择,我们分别执行一百一万,一百万次, 可见执行一百万次改变选择的得大奖的概率为零点六六六六七。 大家看这个图就比较好理解了,最初选择时,有三分之一的概率选择汽车艳阳和碧阳,但是改变选择后的胜率为三分之二。看都看完了,不关注一下再走吗?
1093程序员小帅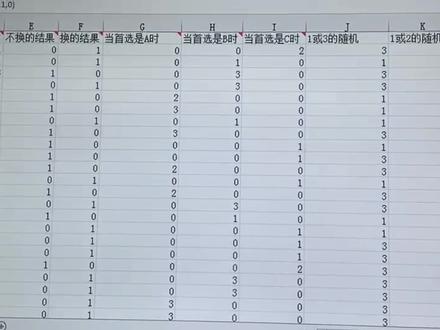 02:06查看AI文稿AI文稿
02:06查看AI文稿AI文稿之前我在网上发的一个三个问题的一个视频,引起了很大的争议和讨论,很多的网友呢就私信我跟我说可以做一个实验跑一下程序,因为他们实在理解不了,他们不相信这个结果。 之前呢,我们用这个 max love 做了一个程序,发到网上去了,但是很多人不理解,所以呢,这次我们就用最简单的 excel 做一个程序跑一下,大家自己也可以回家去模拟跑一下试一试。这里我把公式给大家公开一下。好,我们看一看这个实验首选呢,首选是这个公式, 用这个 rapp 正函数,大家可以看一下 rappe 正函数。然后 这个车在哪一个门门里也要有一个软软的特函数,软软的特函给大家解释一下,就是一个随机数的一个选择,在一到三之间随机选择的一个数,然后这个洞是这个 公式,这里用到一个 a 函数。这个公式,这个公式,这个公式,这里用到了一个 a 函数,用到一个处死函数,大家可以回去查一下 rap 最函数, ok, 这个公式处此函数 rand 最函数。 然后呢,我们得到一个不换的结果,不换的结果是用一来表示,如果不换选到车,我们用一来表示, 如果没有选到,没有名来表示。最终呢,把他们累计,我做了二百次模拟二百次的实验,所以呢,这个不换的结果呢,就是最终的总成绩就是八十次,然后换的结果,换的结果呢总成绩就是一百二十次, 然后因为他们就是随机的嘛,所以我们每次点这个公式都会得到一个随机数,所以我们看呼唤的总成绩就变成五十八,换回 从地变成一百四十二,然后这是概率,五十八除以四十五二百就得出了一个零点二九相当于三分之一,零点七一除以二百相当于四,约等于三分之二的概率。然后我们再模拟一次,随便,只要因为单这是一个随机数字嘛,然后我们只要呃敲这个公式 就会有变化,数据的变化,最终我们可以发现几乎都是三分之一,三分之二。再敲最后一次,你们看约等于三分之一,约等于三分之二。
284原思维说本质 00:36
00:36
猜你喜欢
最新视频
- 3822就这样吧(只爱米莱狄)
- 2087花椒炒肉沫
- 2087花椒炒肉沫











