考研机械设计基础真题成都理工

如图所示，摆动平底，从动件的盘形凸轮机构给了你凸轮的轮廓半径圆，然后圆心是 c 白杆处于最低位置作为初始位置 啊， a b， 俺看到这里标的 a b， 也就是描述的其实就是，嗯，凸轮的旋转中心到它的曲率中心的距离，对吧？然后 o a 的 长也给你了， 让你分析。第一问啊，他说标出凸轮从初始啊，从这个初始位置接触点 b 零到 b 的 时候的转角以及推杆的角位移， 那标转角肯定要用反转法去标了，对吧？那么它处于最低位置，初始位置他说了吗？摆杆最低的时候为初始位置，所以呢，初始位置 b 零是说明是什么处于什么处于机缘的那个位置的时候 啊，也就是说接触点什么在机缘位置，因为只有在机缘，他才是最低位置。所以第一步啊，咱们先要把啥呀？你得把机缘半径划出来，把机缘半径划出来。 机缘半径怎么划？机缘半径是以我突轮的旋转中心为圆心，以突轮的理论拓线到旋转中心的最短距离为半径画圆，那得到的就是机缘 那。呃，凸轮的理论拓线到它旋转中心的最短距离是哪里啊？那就是连接什么呀？连接我们的 o c， 对 吧？它一定在过 o c 的 这条线上， 这边这个焦点其实对应的是最高点，而另一侧的焦点呢，对应的就是最低点，也就是我的理论拓线距离旋转中心的最近位置。比如说我们这里啊，实际上 b 零点已经出来了， 那这里呢，就是我们的 b 零点，然后咱们可以把基圆画出来，以 o 为圆心，以 o b 为半径画圆，那么这个 b 零点啊，是我们，呃，这个 摆动平底，从动键处于最低位置的时候，它的一个接触点， 那我想找到凸轮转角，咱们利用反转法，咱还需要找到什么？他处于最低位置的时候，对应的这个白杆的回转中心，我们得找到。有些同学说，不就是 a 吗？不是 a 啊，我们现在是利用反转法，反转法现在凸轮固定，我们要让这个从动件转， 而我们现在看啊，这个凸轮呢，是逆时针转动，所以说这个白杆呢，应该让它反转法的时候是顺时针转动啊。顺时针转动，那我们就要找到，当它接触点为 b 零的时候，通过反转法，它的白杆的旋转中心在哪里 啊？在哪里？那首先我们要明确啊，反转法我这个白杆的旋转中心一定在以 o 为圆心，以 o 为半径的圆上吧， 对吧？因为你正常转的时候是什么？正常转的时候是这个 a 不 动，对吧？这个 a 不 动，旋转中心 a 不 动，然后我凸轮绕着 o 逆时针转，那你现在反转法就变成了凸轮不动，我的这个 a 绕着啥呀？绕着这个 o 顺时针转，这不就叫反转法嘛，对吧？凸轮不动了，然后我这个 a 呢反过来转，所以说 a 一定在以 o 为圆心，以 o 为半径的圆上，所以咱们要把这个圆画出来啊。 哎，这个蓝色的圆呢，代表的是我们的这个白杆的旋转中心， 通过反转法以后，他应该就是他的一条轨迹，对吧？他的轨迹，那现在接触点是 b 零，我怎么找这个 a 呢？也就是说我怎么找这个 a 零呢？ 那注意啊，我们利用反转法的时候保持的原则是啥？你反转法，你要保证我的凸轮和从动件它的相对运动以及相对位置关系是不能变的。那你，你现在不想反转它正常运动的时候，我凸轮这样 逆时针转我的这个白杆，我的这个白杆是不是永远都要和我凸轮的理论拓线相切啊？ 没有问题吧？所以你反转法的时候，你也要保证这个原则呀，你不能改变它俩的位置关系。所以反转法的时候，我们的这个 a 零、 b 零 也一定和什么相切，和它的理论拓线相切，而我们圆的切线一定是和半径垂直的，所以 a 零、 b 零是怎么样的？垂直于 c b 零的？当然啊，也垂直于 o b， 因为它们都在一条线上， 所以说我们的 a 零点一定在什么？一定在过 b 零且垂直于 c b 零的垂线上吧，对吧？一定在这条垂线上，所以咱们要把这条垂线画出来啊，我们画一下， 哎，过 b 零点做 c b 零的垂线， 那也就是说我们的 b 零点一定在这条。呃， a 零点啊，一定在这条垂线上，而且它又在这个蓝色的圆上，那你说它在哪？那它俩的交点呗。所以其实我们就得到了 a 零。 有些同学说这个垂线他另一侧还有一个呢，对吧？这边垂过来还有一个，他说为什么这不是 a 零，你注意啊，你想象一下，我们是利用反转法，咱们利用反转法， 你想他可能在这个位置吗？如果在这个位置，他就变成什么样子了。变成这样， 那你想我无论是正转法还是反转法？这个 a， 我 们的这个机架永远都在白杆的左侧呀，它再怎么转，它也在白杆的左侧，你这样画，这个机架就跑到白杆的右侧去了，它是不可能存在的， 能懂吧？他是不可能存在这个情况的啊。因此说只有下面这个焦点是符合的，上面是不符合的啊，所以这个不用讨论，因此我刚才做垂线也没有把它垂过来，所以咱们的 a 零就是他啊，刚才涂掉了，咱们再画一下， 这是我们的 a 零位置，有了 a 零位置，它说的是从接触点从 b 零到 b， 我 们的一个转角。那咱刚才说了，凸轮是逆时针转，所以呢，我们反转法呢，就让这个白杆和这个 a 它顺时针转动，让从动键顺时针转， 那它顺时针顺时针转是绕着谁在转？咱刚才说了是绕着 o 在 转，也就是说这个机架 a 绕着 o 在 在转，所以它转过了多少角度是什么？就是这个 o a， 就是 这个 o a 和 o a 零的角度嘛，因此咱要把这个 o a 零连上啊， 连上， 这样我的 o a 零和 o a 的 夹角代表的就是从出使位置到啊，就也就是说从出使位置 b 零到接触点 b 的 时候，凸轮的转角，咱们利用反转法求出来了， 这个位置代表的就是嘚儿它脚，那它还让你求什么了呢？求推杆的脚位移啊。推杆的脚位移，也就是说它在这个过程中啊，我这个推杆它是有一定的摆动的， 对吧？他是有一定的摆动的，他就是从，因为他可以绕着这个 a 在 转嘛，这个大家能理解对不对？所以说他在这个过程中，为了适应我这个凸轮的这个理论拓线的变化，他肯定会有一定的摆动，他让你求的就是这个摆角。 那咱们想他为什么会摆动啊？为什么会摆动？刚才也说了，他是为了适应凸轮的理论拓线，那咱们想他什么时候不摆动， 它什么时候会不摆？不摆动？如果我突轮的旋转中心和它的至心时刻时时刻刻都是重合的，它就不会摆动了， 对吧？那正是因为它的旋转中心 c 和啊，它的旋转中心 o 和它的至心 c， 它时刻都不重合，才会导致它摆动， 是不是这个意思？所以说你想啊，他在这个最低位置，在机缘位置处啊，接触点是 b 零的时候， 他在这样一个位置，如果我的突轮就长什么样子，就长机缘这个样子，就长机缘这个样子。他如果就长这个机缘样子，他的至心和回转中心是不是都是 o 啊？这样的话，他就不摆动了， 对不对？这样它就不摆了吧？那么它摆动以后，它所在的位置是哪里？是 ab， 对 吧？就是这个实际位置 ab 这条线， 那如果不摆呢？不摆，我们只需要现在把这个凸轮的理论拓线就看成这个机缘，它理论拓线就是这个机缘，当它转动到 a 这个位置的时候，也就是说它从 b 零点转动 der 角儿， 然后让这个 a 零转到 a 的 位置的时候，他所在的位置，这就是他不摆动的时候所在的位置。那么当我的 a 零点转到 a 一 的时候， b 零点跑到哪里去了？ 那此刻其实无非就是换了一个理论拓线而已。之前呢是我们题目的理论拓线，现在变成了这个机源作为他的理论拓线了，怎么找？ b 点 是不是过 a 点做什么？做机缘的切线吧，对吧？因为你 b 点，你正常来讲，这里的 b 点是怎么怎么得到的？当然题目本来就有，对吧？那正常 b 点有什么关系呢？和我的这个， 呃，和我的这个图轮的理论拓线，我们讲了 a b 是 和理论拓线相切的，对吧？同样的道理，你现在理论拓线变成了这个机缘，那我的 a b 呢？也要和它相切啊，所以说你现在的 b 点就变成了什么？我过 a 点做我这个 机缘的切线，哎，这个线，比如说我们这里呢，你可以写这是 b 一， 这是 b 一 点，那么我的这个 b 一 点就是啥呀？ 就是我这个凸轮，或者说我这个摆杆啊，摆杆啊，你说推杆也行啊。题目说的推杆一个意思啊，这个推杆不摆动的时候，它， 呃反转法转到 a 点时它的位置，而它摆动的时候，它的位置是啥？摆动的时候就是实际的题目情况的位置，它是在 b 点，所以说它的摆角是多少？不摆动在 b 一， 摆动在 b， 它的摆角是不是就是角 b a b 一 啊， 明白吧？是这个这个原理啊，所以这里就是我们的推杆的脚位以外，也就是推杆的摆角是这样来的。 第二问，标出摆杆的最大角位仪和推程运动角。咱首先呀，先标这个推程运动角，什么叫推程运动角啊？就是我这个凸轮处于推程的时候，它转过的角度，再换句话说，指的是我这个推杆，它的摆角 从最低达到最高的时候，凸轮对应的转过的角度，所以说呢，这个推程运动角和它的最大角位移是什么是对应的？ 因为推程的定义指的就是你的从动件的位移，从这个机缘位置的零达到最大的时候， 凸轮转过的角度代表的就是推乘运动角，而我们这个从动件，它不是这个往复运动的，它不是往复运动的，如果是往复运动的，那就是它的行程 h， 对 吧？就是行程 h， 但它比不是往复运动，它是什么？它是摆动的，所以呢，那就是它从零度到摆动最大角度的时候， 凸轮对应的转角就是推乘运动角，所以这两个是一个位置，能明白吧？你找到推乘运动角，你就能找到最大角位移，因为它俩是对应的，那推乘运动角很好找啊，因为凸轮在这了它最低点的时候，接触点是不是 b 零啊？ 对吧？是 b 零，那它最高点的时候呢？最高点是哪里？就是它对面呀，它最低点其实对应的是它的回转中心和至心连线上啊，回转中心和至心的连线，这是一条非常关键的线啊， 只要是凸轮，这条线非常关键，那么这个回转中心距离凸轮理论拓线最近的位置的接触点，那就是最低点，最高点呢，就是它的回转中心距离理论拓线最远的位置，所以这个点就是我们的最高点 b e， b e 啊，这样的话，我们找到了当它达到最大角位一，或者说它当它达到推成运动角时候的接触点， 那么推乘运动角怎么画？我们讲推乘运动角是 o， 咱们刚才这个怎么画的？就是刚才这个 第一问的，这个转角咋画的？是不是 o a 零和 o a 的 加角啊？然后你来到最高位置就变成啥，那就是 o a 零和 o 什么 o a 一 的加角，所以接触点为 b 一 的时候，你需要把啥？你需要把 a 一 画出来， a 一 画出来以后， o a 零和 o a 一 的加角代表的就是接触点在 b 零时候的 转角，也就是推成运动角。那怎么画？和刚才一样呀？过 b 一 点做切线啊，做这个凸轮理论拓线的切线，也就是说过 b 一 点做什么？做 c b 一 的垂线，一个道理，对吧？因为圆的切线肯定是和它的半径垂直的，所以说咱们就画呗。 哎，这面做垂线啊，大概交在这个点是吧？那这个点的话呢，就是我们的 a 一 点， a 一 点，然后呢，我们要连接 o a 一 o a e， 哎，连上以后推乘运动角指的是哪里啊？就是 o a 零和 o a e 的 夹角，然后注意啊，哪个夹角啊？我反转法，反转法，我的这个， 呃，从动键要怎么转？凸轮是逆时针反转法凸轮，是啊，不是凸轮啊，反转法的话，我的从动键是顺时针，所以是从 a 零顺时针转到 a e 的 时候，这个角度就是我们的推乘运动角 der 零 推推成运动角，有了，对吧？那最大角位移呢？最大角位移其实和刚才的方法是一样的。咱们刚才呢，画了什么？画了他这个转到 a 的 时候，角位移 啊，不是角位移啊，是角位移啊，就是他的转角啊，他的摆角。在 a 点时候摆角是怎么做的？实际上就是过 a 点，我做理论拓线的切线，再做机缘的切线，他俩的什么？ 这两个切线的焦点对吧？加的角度就是我们的角位仪，那最大角位仪呢？最大角位仪只不过就是说你突然达到这个白角最大的时候，或者说达到最最高位置的时候，对应的角位仪。那同样的道理嘛，过 a 一 点干什么？ 做？首先做理论拓线的垂线已经有了，对吧？就是 ab 一， 然后呢，再做什么？再做这个机缘的切线。这里呢，我就不用指，我就不用指了啊，大概这个意思，哎。做机缘的切线，然后呢，它俩的这个夹角就是啥呀？最大角位一， 好吧，其实这个第二问和第一问它的方法都是一样的，你只要能找到 b 一 点，方法是一模一样的。 来，咱们清理了一下啊，太乱了，我们看第三问，他说标出凸轮从初尺位置转过九十度的时候，推杆的角位一，其实一样。这个题啊，你基本上第一问做出来后面的方法就是一模一样的，初尺位置是 a 零对不对？转过九十度说明什么？此刻的 a 跑到哪里去了？ 跑到什么垂直于 o a 零的直线上去了呗。所以说咱们只需要过 o 点做 o a 零的垂线呀。哎呀，这样画直线啊，不要这个咱们画成直线，过 o 点做 o a 零的垂线， 这样的话，它的转角比如说交在我的这个 a 的 这个轨迹上，比如说这是 a 二，那这里是垂直的，这不就代表他转过了啥？转过了九十度对不对？转过了九十度，他跑到了 a 二，然后我们的脚位仪怎么着，怎么画？和第二问以及第一问一样呀，过 a 二点做理论拓线的切线， 再做啥？做基元的切线，那它俩的加角是不是就角为一块撇，这不就完事了吗？那这就是咱们第三问的最终的解法吗？

吉伦机构中采用指挥吉爪主要是为了什么？考察这个吉爪的一个目的，对吧？我们看到这是一个吉轮机构，它的一个基本运行原理是这样的啊，比如说此刻我的摇杆 逆时针的摆动啊摆动，你看在这个逆时针的摆动下，这个吉爪就会给到吉轮一个什么 这个方向的力，对不对？所以他带动吉轮呢，也做一个逆时针转动，当然这是摇杆，摇杆做的是往复摆动，所以当这个摇杆摆动一定角度后，他会带动这个吉轮也转过一定的角度，也就是一般咱们这个吉轮嘛，就是从这个尺一的位置，然后呢 转过一个尺，也就是此刻的尺二呢，会跑到尺一的位置，此刻摇杆就达到了一个极限，就是他 这样转的话，他向左摆动，哎，达到了左侧的一个极限位置，那此刻呢，摇杆就该怎么样了？就该往回走了，所以说摇杆会这个顺时针的往回走，在这个往回走的过程中呢，他是无法带动吉轮运动的，所以在他往回走的过程中，这吉轮是干嘛？吉轮就是静止不动的对不对？ 然后呢摇杆回到原位以后，他再次的逆时针转，然后这个吉轮呢，再继续的跟着他一起转动。所以我们也知道这个吉轮机构他是什么摇杆的一个往复摆动，转化成了一个吉轮的什么间歇转动，他不是时刻都在转， 而我们的指动爪就是为了摇杆啊。咱讲这个摇杆顺时针，他往回转动的时候，吉轮是不动的，你得保证他不能动，你不能让这个吉轮反行程运动，所以你看到如果吉轮想反行程运动，这个指动爪是不干的，因为指动爪在这里顶着你呢，因此这个吉轮转不动， 所以他的目的就是防止吉轮反转。好吧，这是考察这个吉轮的一个基本的运行原理。

给大家分享一个接设计的真题书写我的一个评价案例哈，大家可以看一下，现在是凌晨三点哈，继续熬吧，你们考完我也解放了哈， 继续熬住所有阶段，只拿自己会的，把自己会的一定要准确拿到分数哈，别去做那么多新颖题去。好，咱们来看这个案例， 这是我手里边一个长安的同学哈，他中间一个过程门道，首先看他的选择题，一到五六到十，你可以这样排，填空题一到十二可以这样排下来，对不对？好，关键看解答哈。解答，很多同学的书写逻辑是有问题的，解答怎么写呀？ 你的标准的提纲得分点，加上延伸性的一句话，很多同学连答都不写是不是？然后你要书写清楚你的八分到六分的简答的得分逻辑在哪，得分点给出来之后，后边延伸性的一句话，你不行就强制自己写三行，明白吧。 一般来说，如果不知道写啥，你就想他的原因是啥，是什么造成的后果，有啥东西对不对？把这一想清楚哈，好，再往后走就是到了你看他这个 滑动招生题目看多好，一个一个文字一个公式，一个文字一个公式，对不对？下面就到了大家都有的齿轮受力分一题，这个呢，这个原图不需要腾称啊，当然如果你做题时间比较充裕，你可以腾称，但这个图费了他很多时间，所以说我后来给他建议就说你不需要腾称，你不行就啥呢？ 用文字描述假设一二的捏合点为 a， a 点的受力，分析如下，把这俩错开。还有同学说我要不要在这里去会真那个受力点不需要哈，把它错开一点，要不然你就点差分不清楚，不要在这个鞋盖上画哈，把它错开。还有同学用文字描述也可以，是不是 a 点的受力分析如下，老夸这俩便宜，下来也行， 塞往左看这个轴承体，轴承体呢，很多同学在这里出现问题了，正负号方向镜像反力出错概率很高很高，这里我建议大家复检一下这个位置啊。呃，不少同学都在这里出问题， 下一个出错题就螺栓，这里螺栓严格按照三步走进行螺栓栓状态分析，分析完之后分析单个螺栓，分析危险螺栓受力，随后对螺栓进行强度计算，所有的简化都是要同螺栓所的情况简化。当单个螺栓 在这里大家都出错的点在于螺酸素的状态，那个 c 呀，结合面 i 呀，都分不清楚，要不然就是最终结果。这个第三步，最后一步一点三，这里没有成老问题，明白吧，计算结果都是在这里延伸出来的问题，所以说一定要把基本的数学逻辑搞清楚。 再来就是这个轴系改错，我这里强调一下啊，这个问题比较多，首先呢，你看看你需不需要腾抄，绘图原图哈，如果给你序号你就不需要腾抄了，如果没给你序号是不要腾抄，包括改正，同学上下各一半。 接下来就是关于改错所描述，你看这里哈，很多同学就是说我不知道怎么写，那你就写指数加结果哈，这样话就可以延伸下一行话了。

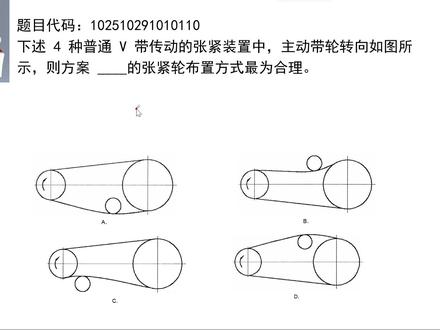
哎，给了你四种张紧带的布置，问你哪个合理？张紧带布置，咱三个字，松 大内。什么意思啊？放在松边，靠近大带轮，而且要放内侧，你一个一个排除呗，你最最方便看的就是内侧， 那 c 肯定就不对了，对吧？你要放内侧， c 很 明显这里是放在外侧了啊，你要让带把它包起来，所以 bc 它都不对啊，排除的很快。然后呢，就是放靠近大带轮，那你看到 a d， a， d 它都是靠近大带轮，那这个没有问题，那我们只能看放松边， 那这是主动轮，我们绕绕入主动轮的是紧边，所以这里是紧边。那你不对啊，这个就放紧边了，对吧？这就错了，那 d 呢？绕入主动轮的是紧边，这里是紧边，那绕出主动轮的上面是松边，所以 d 是 满足的，因此最终选 d 选项就是这么去判断啊。

若将坚顶坚顶从动键改为滚子推杆，其他参数不变。问你运动变化规律，那运动规律是否变化取决于啥呀？取决于理论拓线是否变化。那么如果啊，这是同一个突论机构， 那对于尖底从动线来讲，他的基点就在哪里，就在这个凸轮的这个轮廓线上。也就是说，对于这种尖底从动线来讲，理论拓线和实际拓线是重合的，都是我现在画红的这条线，对吧？ 但是如果你改为滚子呢？那滚子他是怎么样的？他是有半径的。这样的话，理论拓线是指了哪里是滚子至新他走过的轮廓线，那和我们实际的红色线差了一个什么？差了一个滚子半径啊， 对不对？所以说，如果是尖底，这是尖底的理论拓线，而而改为滚子呢？那虚线是滚子的理论拓线，他俩的理论拓线是不一样的呀，因此变化规律他肯定是怎么样？不同的，不同的啊，无论是推程还是回程，因为理论拓线在任何地方都是有变化的。