如何画多边形面积小报装饰

多边形的面积手抄报来了，喜欢收藏起来背电子版！

这个视频张老师和孩子们分享五上数学第六章多边形的面积里面一类非常经典的题型，就是在图形当中减或画最大的图形。 结合两个具体的例题，我们进行分析。首先来看第一个题目，在一个上底为五厘米，下底为八厘米、高为六厘米的梯形中减下一个最大的平行四边形。 减下的平行四边形的面积是多少平方厘米，剩下部分的面积是多少平方厘米？解决这类图形面积题，画图是最关键的解题工具。把文字描述转化成集合图形，能让题目里的所有信息变得直观又形象， 这也是孩子们学习这部分知识必须养成的思考习惯和做题能力。第一步，我们先根据题意画出梯形，标注出上底五厘米，下底八厘米，高六厘米。接下来要在梯形里面剪一个最大的平行四边形， 那这个最大的平行四边形有什么特征呢？核心就是要充分利用梯形的空间，让平行四边形的面积尽可能的最大。梯形有上下两条长度不同的底，要做出最大的平行四边形，就要以梯形的上底作为平行四边形的一组对边， 因为上底更短，能完整贴合。并利用梯形的高，在梯形的下底上再截取和上底等长的线段，找到五厘米所在的端点。 当然，截取这五厘米我们可以从左侧进行测量，也可以从右侧进行测量，道理是一样的。找到这个点之后，连接相对应的顶点，这样就画出了梯形里面最大的平行四边形。 这个平行四边形的底就是梯形的上底五厘米高和梯形的高是一致的，都是六厘米。 根据平行四边形面积公式，面积等于底乘高，就能算出它的面积是五乘六，也就是三十平方厘米。 接下来求剩下部分的面积有两种思考方法。第一步可以先算出梯形的总面积，再减去平行四边形的面积。 梯形的面积公式是上底加下底乘高除以二，也就是五加八的和乘六除以二是三十九平方厘米，再用三十九减三十，得到九平方厘米。 第二种方法就是直接观察剩下的部分，它是一个三角形，这个三角形的底就是梯形的下底，减去上底的差，也就是八减五，等于三厘米高，还是梯形的高六厘米。 根据三角形面积计算公式，面积等于底乘高除以二，就可以求得它的面积是三乘六除以二，也就是九平方厘米。 再来看一道同一个类型的题目，第八小题，这是一道和平形、四边形、三角形面积相关的经典题目。来看题目已知，一个平行四边形的底是八厘米，高是七厘米， 则它的面积是多少平方厘米。若在这个平行四边形里画一个最大的三角形，则这个三角形的面积是多少平方厘米。 这道题目一共有两个问题需要我们求解。第一个问题是求这个平行四边形的面积。题目已经给出了平行四边形的底和高，底是八厘米，高是七厘米。 我们可以直接利用平行四边形的面积计算公式，面积等于底乘高，代入数值计算，就是八乘七，也就是五十六平方厘米。所以这个平行四边形的面积就求解出来是五十六平方厘米。 接下来看第二个问题，在这个平行四边形里画一个最大的三角形，求这个三角形的面积。要解决这个问题，首先要弄清楚在平行四边形里面画的这个最大的三角形到底是什么样的，它有什么特征。 既然要求三角形最大，其实就是要求他的面积最大，怎么让三角形的面积最大呢？我们知道三角形的面积公式就是面积等于底乘高除以二，所以要让面积最大，就要让三角形的底和高尽可能的最大。 因为这个三角形是画在平行四边形里面，所以他的底和高肯定不能超过平行四边形的底和高， 那我们就可以让三角形的底和高和平形四边形的底和高完全对应起来。以平行四边形的一条底作为三角形的底，再以这条底对应的平行四边形的高作为三角形的高，这样画出来的三角形就是这个平行四边形里面面积最大的三角形。 而这样的三角形，它的面积正好是这个平行四边形面积的一半。我们已经算出平行四边形的面积是五十六平方厘米，那这个最大的三角形的面积就应该是五十六除以二，也就是二十八平方厘米。 视频的最后，张老师再给孩子们总结一下在一个图形里减或画出面积最大的另一个图形。这类题目的解析思路和方法， 第一步就是紧扣图形的特点。解题时要紧密结合已知图形的特点，以及要减或画的目标图形的特点， 比如在平行四边形里面画最大的三角形，就要先想清楚平行四边形对边平行且相等面积是底层高的特点，也要明白三角形的面积和底高直接相关。 第二步，要充分利用已知边长和高。要让目标图形的面积最大，关键就是充分利用已知图形给出的底和高，因为图形的面积大多和底高相关，只有让目标图形的底和高尽可能贴合已知图形的底和高，才能最大程度的扩大它的面积。 第三步，确定底和高的取值。结合已知图形的条件，思考目标图形的底和高能取到的最大值。比如在平行四边形里画最大的三角形，就可以直接用平行四边形的底，当三角形的底，用平行四边形的高，当三角形的高。 第四步，结合数据计算面积。确定好目标图形的底和高之后，再带入这个图形的面积计算公式，结合题目给出的数据，就能算出最终的面积是多少。

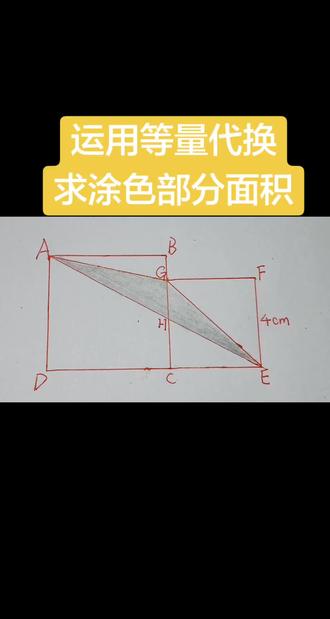
这个视频张老师和孩子们分享一下运用三角形面积公式和等量代换的知识。求图色部分的面积。首先来看题干，如图所示，它是由两个正方形拼成的，小正方形的边长是四厘米，要求求出图色部分的面积。 首先来观察图色部分的图形，从整体上看是一个三角形，当然也能看成是两个小三角形拼在一起的图形。但不管是把它当成大三角形，还是拆成两个小三角形，都找不到它现成的底和高，所以没有办法直接用面积公式来进行计算， 就算给图色部分来加辅助线，分割成其他的图形，也没有办法直接求解。这个时候我们就需要用间接的方法，可以先画一条辅助线连接 a、 c。 接下来我们看三角形 a、 j、 c 的 面积就等于 j、 c 乘 ab 再除以二。 三角形 a、 c、 e 的 面积就等于 c、 e 乘 a、 d 再除以二。这里 j、 c 和 c、 e 都是小正方形的边长，所以 j、 c 等于 c、 e、 ab 和 ad 都是大正方形的边长，所以 ab 等于 ab。 这样以来，三角形 a、 j、 c 和三角形 a、 c、 e 就是 等底等高的三角形，它们的面积肯定相等。 为什么要研究这两个三角形呢？因为它们有一个共同的部分，就是三角形 a、 c、 h。 用面积相等的三角形 a、 g、 c 和三角形 a、 c、 e 分 别减去这个共同的三角形 a、 c、 h， 剩下的部分面积肯定也相等，剩下的部分就是三角形 a、 g、 h 和三角形 c、 e、 h， 所以 这两个三角形的面积是相等的。 这一步等量代换之后，原图里边的土色部分的面积就可以转化成三角形 g、 c、 e 的 面积了。我们知道 c e 和 c g 都是小正方形的，边长也就是四厘米。再根据三角形面积公式，面积就是底乘高除以二，也就是四乘四除以二等于八平方厘米， 所以图色部分的面积就是八平方厘米。最后总结一下，这道题的解题关键就是通过辅助线找到面积相等的三角形，再利用等量代换得出三角形 a、 j、 h 和三角形 c、 e、 h 的 面积相同。 把不好计算的图色部分转换成容易计算的三角形 c、 e， 也就是综合运用三角形面积公式和等量代换的知识，间接求出图色部分的面积。

我们今天来挑战五星学霸多边形面积的新素养题，这道题求图色部分的面积是一个不规则的图形，看看怎么样巧妙地解决。 我们再看一下这道题，这是一个正方形，求的是图色部分的面积，我们一起读一下这道题。正方形 a、 b、 c、 d， 它的边长是十二厘米， e、 f 呢是 这个边的中点，求图色部分的面积。那我们分析一下这道题，图色部分呢是一个不规则图形，我们要求它的面积就是把大正方形的面积求出来，再减去空白的部分的面积，就是图色部分的面积了。 好，我们看一下，思路就是这样求图色部分的面积，用整个正方形的面积减去空白部分的面积，那正方形的面积知道它的边长是十二了，所以它的面积就是十二和十二乘以十二，这个非常好求。那我们的关键点就是求空白部分的面积。 我们发现空白部分它也是一个不规则的图形，但它是由三角形组成的，我们这时就要借助辅助线先连接一下 b、 g， 这里呢就把空白部分分成了四个三角形，我们给它标上号，一号、二号、三号、四号，我们只要把一、二、三、四号的面积求出来，相加就是空白部分的面积了。 好，我们逐个分析一下。先看三角形一和三角形二，因为告诉了 e、 f 是 这个边的中点，也就是 e 是 中点，那就说明 a、 e 是 等于 e、 b 的。 那我们看一下三角形一和三角形二， 对于一和二来说，也就是它们的底是相等的，因为 a、 e 等于 e、 b， 再看一下它们的高呢？ 我做的这条线呢，就是三角形一和二的高，它们的高也是相等的，那等底等高的三角形，那面积自然也是相等的，所以我们推导出来，一号的面积就等于二号的面积， 那同理，我们看一下三号和四号，因为 f 是 b、 c 边上的中点，那就说明 c、 f 就 等于 f、 b， 那 我们做一下三号和四号的高，看一下， 我们发现三号和四号，它们的高也是相等的，那就证明了三号的面积也等于四号的面积，因为它们也是等底等高。 接下来我们看一下二号三角形和三号三角形，我们发现它们的这两条高是相等的，那底也是相等的，因为 e、 b 是 这个边长的一半，应该是六，那 f、 b 也是六等底等高的话，可以推出二号的面积也应该等于三号的面积， 那一号等于二号，三号等于四号，二号又等于三号，那就说明这个一、二、三、四都是相等的， 就是这几个小三角形的面积是相等的，因为一二、三、四号，它们都是等底等高。那么我们接下来就要看它们的面积分别是多少。我们看一下三角形 e、 b、 c， 我 给它圈一下 那三角形 e、 b、 c， 我 们发现它等于二三四相加，我们写一下三角形 e、 b、 c， 它的面积就等于二加三加四， 那么 e、 b、 c， 它的面积我们能不能求出来呢？ e、 b 是 等于六，因为是边长了一半，那 b、 c 呢？刚好是边长十二，所以我们根据三角形的面积公式，用底底就是十二乘以高是六，然后再除以二，就可以得出三角形 e、 b、 c 的 面积，算一下，它是三十六平方厘米， 那因为二三、四是相等的，所以我们可以把它写成就是三倍的二号三角形，三倍的二号三角形等于三十六，我们就可以推出，那二号三角形就等于三十六，除以三可以算出来是十二平方厘米， 因为一二三四的面积是相等的，那求出来一个就知道了，四个一二三四，一等于二等于三等于四，都等于十二平方厘米。那现在呢，我们可以就把空白部分的面积求出来了， 空白部分就是一加二加三加四，这四个三角形相加，就等于十二乘以四 等于四十八平方厘米。那我们涂色部分的面积是用大正方形的面积减去空白部分的面积，所以我们可以求出涂色部分的面积 就等于大正方形的面积是十二乘以十二，边长乘以边长，再减去空白部分的四十八平方厘米，计算一下应该是九十六平方厘米，所以空白部分的面阴影部分的面积就求出来了。记得点赞关注哦！