六年级95页的扇形怎么画
来吧,六年级的同学们,黑板上的这道题你们有思路吗?这道题是来自于人教版六年级数学上册同步练习册上的一道拓展题, 如图,这是一个圆心角为四十五度的扇形,其中等腰直角三角形,它的斜边长为六厘米,让我们求阴影部分的面积。看到这道题,很多学生啊,都交了白卷了,各位 不知道怎样去做?其实这道题很多同学的思路就是我,我要求出以圆心角为四十五度的这样一个扇形,这个面积能求出来,因为这个半径是六, 那关键这个三角形它的面积直接求,没法求,因为只知道了斜边,那么这两个边长度没有告诉我们。其实这道题我们可以这样分析,既然这是四十五度对不对? 那如果我再找一个和他面积完全相同的给他,并在一起,那么他将变成,各位啊,我又找了一个,那王老师在这里呢,我简单的来画一下,画一画啊,当然我画的呢,可能不一定标准, 那么同学们来观察,现在这两个面积是不完全相同了,这个角四十五度,那这个角是不是也是四十五度,那这个角是不是就是一个九十度? 因为这两个面积是相同的,那么我们是不是就可以用这个整个这个大扇形的面积啊,减去这个等腰直角三角形的面积,这个是六,这个是不是也是六啊? 然后我再除以二,是不是就直接求出阴影面积?哎,王老师你这个方法太好了,那我们一起来求。圆形角是九十度,那么圆面积的四分之一圆的半径是六,所以就是三点一四 乘六的平方,然后再除以四,我们很好算这个啊,来,六六三十六,三十六,除以四是九九派,九派是二十八点二六平方厘米, 这是这个大扇形的面积。那我再求出这个直角三角形的面积,直角边都是六厘米,所以直角三角形的面积是底层高,然后除以二 六六三十六,除以二是十八平方厘米。我用这个大扇形的面积减去这个大直角三角形的面积,就是这两部分,阴部分面积也是二十 八点二六减十八。那我求出的是上下两个完全相同的应用面积,所以我还得再除以二,就能求出其中的这一个应用面积。 二十八点二六减十八是十点二六,十点二六,除以二呢,是五点一三平方厘米。那对王老师所讲的这个题,这个方法你学会了吗?如果你也喜欢王老师的视频啊,给王老师点赞、关注、收藏,起来教娃吧!
粉丝122.4万获赞590.0万
相关视频
 02:12查看AI文稿AI文稿
02:12查看AI文稿AI文稿同学你好,这节课我们来学习扇。行,再来完成一个问题, 画一个半径两厘米的圆,再在圆中画出一个圆心角,是一百度的扇形。好,首先我们画出一条 半径是两厘米的圆,半径两厘米,旋转一周,这样我们就得到了一个半径是两厘米的圆, 这时我们要画圆心角,是一百度的扇形,我们要借据工具,什么工具?两脚气 圆心,再点欧刻度线与半径重合,找到一百度 点住点,然后利用直尺通过圆心在圆上做出另外一条半径标上点 b, 这时角 aob 就是一个圆心角,是一百度的扇形了。 学习了新知,你有哪些收获呢?赶快和老师来总结一下今天的学习内容。 今天我们学习了扇形,知道了一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形, 同时知道顶点在圆心的角叫做圆心角。还知道在同一个圆中,圆心角越大,扇形就越大,反之,圆心角越小,扇形就越小。 你记住了吗?这节课就上到这里,没有听懂的同学,请你再仔细的看一遍,再见!
148点通互动微课堂 05:11查看AI文稿AI文稿
05:11查看AI文稿AI文稿六年级今天我们来学习扇形统计图拓展题,妈妈从单位下班交车到菜市场买菜,再步行回家。 第一题,观察图号,坐公交的时间是买菜的百分之几,百分号前保留一位小数。 首先我们先看图二,这个图表示离家距离与时间的关系图,它的横轴表示经过时间,它的正轴表示离家的距离。那妈妈 是从单位下班回家的,所以最开始距离家的这个路程是三点五千米。那先乘公交车,那就乘公交车到菜市场后, 其实也就是在这个位置,他到菜市场了,那这时候离家的距离就是一千米,然后去买菜,你看这段 路程对应的时间,经过的时间是十分钟,因为从零到十,也就是十分钟。那接下来他去买菜, 买菜后再步行回家,那买菜的过程当中,他距离家的这个路程是不变的,都是一千米,所以这段时间里面他就是去买菜的这段对应的时间就是从十分钟到二十四分钟, 我们就可以用二十四减十,也就等于十四分钟。那这个十四分钟就是妈妈买菜用的时间。 你看坐公交十分钟,买菜十四分钟,求一个数,是另一个数的百分之几。我们用的方法是除法计算,所以用十除以十四,因为十除以十四,它是无限小数。 那现在要求百分号前保留一位小数,所以我们先给他保留三位小数, 那么我们就先看前面的四位,零点七四二,那你看保留三位小数,我们就看小数的第四位,二二不满五。所以呢,舍去,那就约等于零点七一四, 要改成百分数,那就小数点向右移动两位,变成七十一点四,在天上百分号。所以坐公交的时间是买菜的百分之七十一点四。 第二题,观察图二、公交车每分钟行几千米 公交车坐的这段时间是十分钟,那这段路程呢?它是从三点五到一,所以路程我们就用三点五减一求出来是二点五千米, 二点五千米花的时间十分钟。那球每分钟行多少千米,你就用路程除以时间求出来就是速度,所以每分钟行零点二五千米。第三题,观察两幅图, 妈妈从单位下班先买菜再回家,一共用了多长时间? 第一幅图,时间分配统计图。从图中我们能看到,把买菜、步行回家和乘公交车的总时间看作单位一。其中步行回家的时间是占 四分之一,因为这个扇形的圆心角是九十度,那么一个周角是三百六十度。九十度除以三百六十度, 等于四分之一,所以步行回家的时间是占四分之一的。 那买菜和坐公交的这个时间合起来,就是一减四分之一,等于四分之三。 这两部分合起来,时间是占总时间的四分之三。做这两件事情一共花费的是二十四分钟, 二十四分钟占总时间的四分之三,所以我们用二十四除以四分之三求出来,等于三十二分钟。 所以妈妈从单位下班先买菜再回家,一共用的就是三十二分钟。
349豆豆老师•家长课堂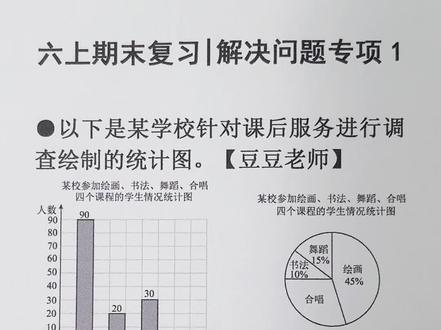 04:26查看AI文稿AI文稿
04:26查看AI文稿AI文稿六年级今天我们进行期末复习解决专项一、以下是某学校针对课后服务进行调查会制的统计图, 这里有两个统计图,第一个是这个学校这四门课程学生情况统计图,横轴表示四门课程,纵轴表示人数。那第二个统计图 他是这个学校四门课程学生情况统计图,这是一个扇形统计图,里面表示四门课程的占比,也就是分率。 第一题一共调查了多少名学生,并将条形统计图补充完整。首先我们看 这个四门课程,在条形统计图当中,我们可以看到这三门分别有多少人,但是合唱的这门课程 他的人数未知的,所以不能求和。那这时候我们要结合第二个扇形统计图当中的数据来看。例如说你看书法, 他的人数是在四门课程总人数的百分之十,那说法的人数是二十人,也就是总人数的百分之十是二十人,那么总人数我们就可以用 二十除以百分之十求出来,等于两百名学生,那说明调查的学生一共是有两百名。然后我们要将条形统计图给他补充完整。你看两百名学生, 合唱的学生是几人未知,那我们就要补充。你看绘画九十,书法二十,舞蹈三十,合起来是一百四十人,那把两百 减去一百四十,等于六十人,那就说明合唱是有六十人,那六十在这个位置,那么我们就对应过来,画出条形通缉图, 记得标上数据六十。第二题,参加合唱的学生占参与调查学生的百分之几,你看把四门课程的学生的总人数看作单位一, 其中书法占百分之十,舞蹈占百分之十五,绘画占百分之四十五,所以我们用一减去这三门课程的 分率和,就是百分之十加百分之十五加百分之四十五,合起来是百分之七十一,减百分之七十等于百分之三十,所以参加合唱的学生 占参与调查学生的百分之三十。第三题,参加舞蹈课程的学生比参加书法课程的学生多百分之几。 你看舞蹈课程的学生是三十人,书法课程的学生 是二十人,我们就用三十减二十求出来是十人多的十人。跟什么比?比参加书法课程 学生多百分之几,所以比的后面书法课程的学生就看作单位一,那就再除以书法的二十 会等于十,除以二十等于零点五,零点五,也就是百分之五十,那就多百分之五十。
333豆豆老师•家长课堂 00:58查看AI文稿AI文稿
00:58查看AI文稿AI文稿来看题目四,某校六年级有一百二十人,英语竞赛中优秀的二十四人占六年级学生的百分之多少。 若制成扇形统计图,对应的扇形圆心角的度数为多少度,告诉了六年级的总人数一百二十人,优秀的二十四人,那么优秀的人数占六年级的百分之几, 求一个数是另一个数的百分之几是多少?用除法计算,所以用二十四优秀的人数除以总人数 等于零点二,等于百分之二十。若制成扇形统计图,对应的圆心角是多少度呢?周角是三百六十度,那百分之二十,它也就是三百六十度的百分之二十, 所以用三百六十度乘百分之二十,等于七十二度,所以这里的圆心角是七十二度。那这道题应该选择 d。
173大王教数学 03:17查看AI文稿AI文稿
03:17查看AI文稿AI文稿大家好,我是孙老师,今天我给大家分享的是六年级上册扇形统计图,我们一起来看黑板上的题。 已知棉花的种植面积比油料的种植面积多三十公顷,根据统计图回答一、三种作物共种了多少公顷?首先我们先来看 上行统计图,粮食占了总数的百分之六十,棉花占了总数的百分之二十五, 我们可以求出油量所占的百分比,我们把整个圆看作一,也就是百分之百求出油量所占的百分比,用一减百分之六十,减百分之二十五等于百分之十五。 好,再来根据这句话,棉花的种植面积比油料种植的面积多三十公顷。 让我们求的是三种作物共种了多少公顷。求我们可以用对应的数来除以对应的分率。 这三十公顷呢,指的是棉花比油量多重的,它对应的分率也就是百分之二十五减去百分之十五, 所以用三十除以括号,百分之二十五减百分之十五,括号等于三百公顷来看第二问, 油料种了多少公顷?棉花种了多少公顷?我们由第一问可以知道,总的是三百公顷,油量占了总数的百分之十五,所以用三百乘以百分之十五等于四十五公顷, 棉花占了总数的百分之二十五,总数是三百,也就是三百乘以百分之二十五等于七十五公顷。我们来看第三问, 粮食比棉花多重了多少公顷?我们先算出粮食占了总数的百分之六十,总数是三百。 三百乘以百分之六,算出粮食的有多少公顷。再减去棉花的七十五公顷,也就是多重的三百乘以百分之六十, 减七十五,等于一百零五公顷。我们来看第四问,油料的种植面积是棉花的百分之几, 带柿子的我们要用除法,用油料的面积来除,以棉花的面积, 再转化成百分数四十五除以七十五乘以百分之百,等于百分之六十。好了,我的分享到这里,感谢您的聆听。
13小孙老师数学课堂 06:38查看AI文稿AI文稿
06:38查看AI文稿AI文稿我们今天来学习选择合适的统计图,那在每个小学阶段的话,我们学过的统计图,这个是条形统计图,这个是折线统计图,这个是扇形统计图, 那他们每个图形的话都有他们各自的特点啊,条形统计图的话,他是能够清楚的看出数量的多少。折线统计图啊,他的话能够直观的看出数量的变化趋势。扇形统计图的话,他能够 看出的话呢,各部分数量与总量之间的一个关系啊,这就是我们三个图形的话它的区别。如果说我们要表示某一个数量的多少的话呢,我们就要选择用我们的条形统计图,如果说我们要选择它的一个变化趋势, 就选中的折线统计图,而我们的扇形统计图的话,它是表示各部分与总量之间的一个关系。所以的话,这三个统计图的话是我们整个小学阶段呢学的根据他们的特点来选择合适的 统计图。我们看第小题,他说关心他人,奉献爱心。我是某中学举行慈善一日捐活动,活动中七年级一班五十名学生自发组织 献爱心捐活动啊,班长的话将捐款的情况进行了统计,并绘制成了条形统计图啊,根据图中提供的信息,全班同学捐款的总金额是多少? 他要求的是全班同学捐款的总金额,那我们的话捐十元的有六人,捐款的总钱的话是六乘以十等于六十元, 这是我们抖团,捐十元的,捐二十元的有十三人,那就是他们十三人,捐的款的话就是十三乘以二十二百六十元, 然后捐三十元的有二十人,那就是三十乘以二十等于我们的六百元。捐五十的有八人,那就是五十乘以八等于四百元。捐一百的有三人, 那就一百乘以三就等于三百元。要算的是全班同捐款的总金额,那我们已经算出这些钱的话,我们再总共加起来,那这里的话就是我们的六十,加上我们的二百六十,再加六百, 再加四百,再加三百,等于一千六百二十元啊,那所有的话,我们就会算出全班的话捐款的金额是一千六百二十元。这是我们来看一下第二题啊, 他说小王家今年的一到五月份的用电量情况如图所示,则增长率最大的是几月份啊?是几月份增长率最大。首先我们来看一下,一月份是一百二十千瓦,二月份是一百千瓦时, 三月份是一百一,四月份是一百二十五,五月份是一百千瓦时,那我们增长率最大的话,我们要知道增长率的话是用增长的量除以我们的原来的量, 那在这里的话呢,增长率最大,首先的话呢,肯定是线的话,增长呢可是往上走,所以我们的一月份到二月份的话,他是负增长,然后我们的四月份到五月份是负增长,所以我们要算增长的,我们只需要算 二月份到三月份就是三月份的增长率,还有到三月份到四月份,四月份,这只需要算三月份和四月份的增长率就可以了,我们看一下三月份的增长率怎么算啊? 三月份的增长率呢?三月份是一百一十千瓦的用电,然后减去二月份一百的用电量,然后再除以我们二月份,他是和二月份做比较,再乘以 百分之十,这是三月份的增长率,那么四月份的增长率呢?四月份是一百二十五千瓦时,然后三月份是一百一十千瓦,它的增长的量就是我们四月份的量,减去我们三月份的量,再除以三月份 乘以百分之百是百分之十三点六,所以的话我们三月份它的增长率是百分之十,四月份的增长率是百分之十三点六,所以的话增长率最大的话呢,它瘦是我们的四月份, 这是我们的这一题啊,这题为什么我没有算二月份和五月份呢?因为的话一月份到二月份的话,它是降低, 所以说他的增长率是负增长。然后四月份到五月份的话呢,他五月份这里的话是一百千瓦,他也是负的,他也是在降,所以的话我就直接考虑增长的这两个月啊,三月份和四月份,这是我们的第二小题啊。三题,他说某中学的话,七年级若干名同学的室内调查情况,如图, 假性近视的同学有六十人。假性近视啊,这里 b 的 话呢,这里是假性近视, 然后假性近视的同学比近视的同学多多少人啊?假性近视的同学的话占的是我们总人数的百分之三十, 然后的话他假性近视的同学是六十人,这百分之三十对应的是六十人。然后他要问的话呢,是假性近视比近视的同学,那么近视的话,这个角它是九十度,那这个角是九十度的话,那他所占我们整个图的百分之二十五啊, 这个是我们用圆形角去除,以三百六十度的话就得到,这个扇形的话占整个圆的四分之一,那它化成百分之的话就是百分之二十五。那么看一下,要我们求我们假近视,假性近视等于比近视等于多多少人,那我们肯定要算出我们的 近视的同学,那在我们算近视同学的话,我们要先算出总数,因为哪些近视的这六十人的话,对应的率是百分之三十,那所的我们量取率的话就会求出总数,那就是六十除以百分之三十算出来两百人, 我们的话近视的同学,那么近视的同学的话呢?是不是可以算出来,那么就是两百乘以百分之二十五就得到我们近视的同学的话是五十人,这里的话是近视的同学, 近视的同学是五十人,那么假性近视的是六十人,那么假性近视的同学比近视多多少人,那就减出来等于我们的十人,所以这个空填的是我们假性近视比近视的同学多十,这是用扇形统计图来解决问题。
 17:38查看AI文稿AI文稿
17:38查看AI文稿AI文稿同学们大家好,这节课我们继续对本学期的知识进行整理和复习。这节课要复习的主题是元,请同学们想一想,关于元,本学期我们学过哪些知识呢? 我们可以从以下几方面进行整理和归纳,圆的认识,圆的周长,圆的面积还有扇形。首先我们来看有关圆的认识这一部分内容的整理,请同学们回忆一下圆的各部分名称都是什么呢? 在一个圆中,它的中心就是圆心,一般用大写字母 o 来表示。连接圆心和圆上任意一点的线段是圆的半径,用小写字母二来表示。通过圆心并且两端在圆上的线段是圆的直径,用小写字母 d 来表示。 在回忆了圆的各部分名称后,想一想圆有哪些特征呢?在同一个圆中,直径是半径的二倍,也可以说半径是直径的二分之一。圆是一个轴对称图形,像这样的对称轴可以画无数条。 那么怎样画一个圆呢?我们可以借助圆规来帮忙,圆规两角之间的距离就是所画圆的半径。 在回顾了圆的认识这部分内容之后,我们继续来看圆的周长。第一个问题,什么是圆的周长呢? 像这样的围成圆的曲线的长是圆的周长。在此基础上,我们认识了圆周率。 圆的周长比直径总等于一个固定的数,这个数就称为圆周率。用字母派来表示。派是一个无限不循环小数计算中通常派取三点一四。 在认识了圆周率的基础上,我们学习了圆的周长的计算方法,可以利用 c 等于派 d 或 c 等于二派二来计算圆的周长。接着我们来看圆的面积。同样的第一个问题,什么是圆的面积? 圆的面积就是它所占平面的大小,那么圆的面积该怎样计算呢?请同学们回忆一下推导过程。 通过减拼法将圆转化成了近似的长方形。根据长方形的面积公式,我们就得到了圆的面积的计算公式, s 等于 pi 二的平方。在转化过程中体现了划趋为值的重要思想。 在学习了圆的面积的基础上,我们又认识了圆环。像这样的两个半径不相等的同心圆之间的部分就是圆环,外圆的半径一般用大写字母二来表示,内圆的半径一般用小写字母二来表示。 圆环的面积该怎样计算呢?我们可以利用外圆面积减内圆面积,求圆环的面积用字母表示为 s, 等于派乘大二的平方,减派乘小二的平方, 根据乘法分配率还可以表示为 s, 等于派乘大二的平方,减小二的平方的差。 同样是在学习了圆的面积的计算方法的基础上,我们还讨论了两种圆的面积的应用问题,外方内圆和外圆内方。 在外方内圆、中方与圆的关系是,正方形的边长等于圆的直径。在外圆、内方、中方与圆的关系是,正方形的对角线就是圆的直径,并且正方形的两条对角线相互垂直。 借助这些关系,我们就可以求正方形的面积,圆的面积以及正方形和圆之间部分的面积。以上就是圆的面积这一部分我们所学习的内容。最后来看扇形。什么是扇形呢? 一条湖和经过这条湖两岸的两条半径所围成的图形叫做扇形。在扇形中有圆心角的存在,像角 a、 o、 b 这样顶点在圆心的角叫做圆心角。 扇形的大小和圆心角的大小有关,也和扇形所在圆的半径大小有关。 这样我们就完成了对圆这部分知识的整理和归纳。接下来我们再通过一些练习,进一步的巩固学过的知识。首先请你来判断下面的说法正确吗?第一小题圆周率派,就是三点一四 圆周率。 pi 其实是一个无限不循环小数,在没有特殊说明的情况下计算时通常保留两位小数,取三点一四,因此三点一四是 pi 的 近四值,而不能说 pi 就是 三点一四,这个说法是错误的。 第二小题,两个圆的直径相等,它们的半径也一定相等。由直径相等可以知道这两个圆是等圆,因此它们的半径也是相等的,这个说法是正确的。 第三小题,半径相等的两个圆周长相等。根据圆的周长的计算方法, c 等于二派二,可以知道这个说法是正确的。 第四小题,圆的半径扩大到原来的二倍,周长和面积也扩大到原来的二倍。同学们是怎样思考这个问题的呢? 在这里我们分享几种解决这个问题的思路。第一种思路,假设法,假设原来圆的半径是一厘米,那么扩大后圆的半径是两厘米。 通过计算可以知道,原来圆的周长是六点二八厘米,扩大后圆的周长是十二点五六厘米,扩大后是扩大前的二倍。 再来看面积,同样通过计算,原来圆的面积是三点一四平方厘米,扩大后圆的面积是十二点五六平方厘米,因此,扩大后圆的面积是原来面积的四倍。 所以,当圆的半径扩大到原来的二倍时,周长扩大到原来的二倍,面积扩大到原来的四倍。所以题目中的这个说法是错误的。 再来看第二种思路,利用公式进行推导。扩大前的半径可以用字母二来表示,那么周长可以表示为二派二,面积是派二的平方。 当半径扩大到原来的二倍后,可以用二二表示现在的半径,那么现在的周长等于四派二,现在的面积等于四派二的平方。 对比一下,扩大后的周长是扩大前的二倍,扩大后的面积是扩大前的四倍,也得到了刚刚的结论。 第三种思路,利用比,我们可以得到一个更为一般性的结论,如果用二一二二分别表示两个圆的半径,那么两个圆的周长比 c, 一 比 c, 二化简后就等于二一比二二, 两个圆的面积比 s, 一 比 s, 二化简后就等于二一的平方比二二的平方。 因此,如果我们把圆的半径扩大到原来的二倍,理解为现在的半径和原来的半径比为二比一, 那么周长比就是二比一,面积比是二的平方,比一的平方也就是四比一。这样就得到了刚刚的结论,周长扩大到原来的二倍,面积扩大到原来的四倍。在完成了这组判断问题后,我们再来看一组填空问题。 第一小题,一个圆的半径和直径的比是多少?根据在同一个圆中 d 等于二二这一关系可知,同一个圆的半径和直径的比就是一比二。 第二小题,甲、乙两个圆的半径分别是二厘米和三厘米,它们的直径的比是什么?周长的比是什么?面积的比是什么? 借助我们刚刚分享过的思路,如果用二甲二乙分别表示两个圆的半径,刚刚得到的结论是,周长比等于半径比,面积比等于半径的平方比。 与此类似的,我们也可以得到两个圆的直径比其实也等于半径比,由此就可以完成这道填空了。它们的直径的比就是二比三,周长的比也是二比三。面积的比是二的平方比,三的平方也就是四比九。 接下来看第三小题。在一张长八厘米、宽六厘米的长方形纸片上画一个最大的圆,这个圆的半径是多少厘米?如果画一个最大的半圆,这个半圆的半径是多少厘米? 这个问题该怎样解决呢?请同学们动手试着画一画吧! 我们一起来分析一下,如果在这样一张长方形纸片上画一个最大的圆,可以怎样画呢? 之前我们曾经讨论过在正方形中画最大的圆的问题。圆的直径就等于正方形的边长。在长方形中,与正方形不同的是,长和宽是不相等的。如果我们要画圆,该以哪条边的长作为直径呢? 如果以长作为直径可以吗?显然,这个圆不能完全画在长方形纸片上。 在长方形纸片上能够画出的最大的圆,其实是以宽为直径的圆,因此它的直径就等于六厘米,那么它的半径是三厘米。接下来想一想,如果要画一个最大的半圆呢?方法和画整圆是一样的吗? 我们试试看,如图所示,这是以长方形的宽为直径所画的半圆。想想看,这个半圆是最大的吗? 这一次如果用长方形的长作为直径,能不能在长方形纸片上画出这个半圆呢? 我们再来试一试,如果以长方形的长八厘米作为直径画半圆,那么这个半圆的半径就是四厘米,而长方形的宽是六厘米。显然,这一次以长方形的长为直径的半圆是能够画在长方形纸片上的, 因此,这个半圆才是长方形纸片上最大的半圆,它的半径是四厘米。 我们就这个问题再延伸一下,请同学们想一想,在长方形纸上画最大的半圆,一定是以长方形的长作为圆的直径吗?如果像这样的长方形又会出现什么情况呢? 显然,这一次如果我们仍然以八厘米作为直径,这个半圆就没有办法在长方形纸上画全了。这是由于长方形的宽只有三厘米,而半圆的半径有四厘米。 因此,在像这样的长方形纸上画最大的半圆的问题,我们不仅仅要考虑长方形的长与半圆直径之间的关系,还要考虑长方形的宽与半圆半径之间的关系。 请同学们课后在不同的长方形纸上试着画一画其中最大的圆和最大的半圆吧, 这样我们就完成了这组填空问题。接下来我们来看一道解决问题。如右图,街心公园有两块半圆形的草坪,他们的周长都是一百二十八点五米,这两块草坪的总面积是多少? 如果我们把这两块半圆形的草坪拼一拼,可以发现,原来要求的这两块草坪的总面积其实就是圆的面积。想要求圆的面积,就要知道圆的半径。那么如何根据已知条件,这两个半圆的周长都是一百二十八点五米来求半径呢? 我们以一个半圆来进行分析。先来描一描这个半圆的周长,它包括圆周长的一半 和一条直径的长,因此可以写作 c。 半圆等于二,派二乘二分之一,这是圆周长的一半,再加上二二,这是直径的长度,整理一下就等于派二加二二。 根据乘法分配率将相同的因素二提取出来,也可以写作派加二的和乘二, 因此根据半圆的周长等于派二加二二。第一种方法可以用方程的方法解决问题。设半圆的半径是 x 米, 那么在派取三点一四的情况下,这个方程可以列为三点一四, x 加二 x 等于一百二十八点五。解这个方程可以得到 x 等于二十五,也就是半圆的半径是二十五米。 这样在已知半径的情况下,我们就可以求整圆的面积了。三点一四乘二十五的平方等于一千九百六十二点五平方米完成达画。 如果不用方程方法,还可以怎样解决这个问题呢?可以借助刚刚的研究结论,半圆的周长等于派加二的和乘二。 那么在派取三点一四时,我们就可以用半圆的周长一百二十八点五除以三点一四加二的和,求出半径等于二十五米。在此基础上,利用三点一四乘二十五的平方求出这两块草坪的总面积,结果和刚刚是相同的。 再来看这个问题,如图,中间是边长一厘米的正方形,与这个正方形每一条边相连的都是圆心角为九十度的扇形。整个图形的面积是多少? 根据中间是边长一厘米的正方形,我们可以知道,周围这四个圆心角为九十度的扇形,它们的半径也都是一厘米。 因此,如果像这样进行一下平移,这四个扇形就可以拼成一个完整的圆,这个圆的半径是一厘米, 因此要求的图形的面积其实就是求半径为一厘米的圆的面积,加上边长为一厘米的正方形的面积。因此可以列式三点一四乘一的平方,加上一乘一,计算后,等于四点一四平方厘米。完成答话 再来解决一个实际问题,如图,学校操场的跑道由正方形的两条对边和两个半圆组成。小陈在操场上跑了五圈,一共是多少米? 由操场的中间是一个正方形,可知两边的两个半圆的直径都是五十米。小陈在操场上跑一圈的距离如图所示,这其中包括两个半圆中弧的长度, 如果平移一下,这两段弧的长度合起来就是整圆的周长。除此之外,还有两条正方形的边长。 因此我们可以列式三点一四乘五十求圆的周长,再加上五十乘二,求正方形的两条边长,通过计算等于二百五十七米。 这说明在学校操场的跑道上跑一圈的距离是二百五十七米。小陈跑了五圈,因此用二百五十七乘五求得一共是一千二百八十五米。完成答话。 最后,我们再来看这样一个问题,从半径二分米的圆形纸里减去一个最大的正方形,剩下多少平方分米的纸? 如右图所示,这其实是一个外圆内方的问题。由半径十二分米,我们可以先求出直径十四分米,那么正方形的面积就可以利用二分之一乘四乘二的积,再乘二等于八平方分米, 圆的面积用三点一四乘二的平方等于十二点五六平方分米,这样剩余部分的面积就是十二点五六减八等于四点五六平方分米。完成答话。 这是一种方法,我们也可以借助在研究外圆内方问题时所得出的结论。如果圆的半径用二表示, 直径就可以表示为二二,这样正方形的面积就等于二二的平方,圆的面积是派二的平方,正方形和圆之间部分的面积可以表示为派二的平方减二二的平方。 当派取三点一四时,这个式子可以写作三点一四二的平方。减二二的平方等于一点一四二的平方。当二等于二分米时,一点一四二的平方就等于一点一四乘二的平方等于四点五六平方分米, 和我们刚刚的计算结果也是一致的。好了,在本节课的复习中,我们在梳理了圆这部分知识的基础上,通过一些练习巩固了所学的知识。请同学们课后按照自己喜欢的方式也整理一下圆的相关知识吧。
22名师课堂 03:31
03:31 02:46查看AI文稿AI文稿
02:46查看AI文稿AI文稿今天让我们来做一道关于扇形统计图的问题。首先我们先来读题,下图是某商场一个月的营业额统计图,如果斜末部这个月的营业额是六点二万元,那么家电部这个月的营业额是多少? 做完题目,我们来看这个图,嗯,家电的占这个一个月营业额百分之四十二,服装类占百分之二十五,鞋帽类占百分之二十,食品类占百分之五,其他的占百分之八。 我们再来看他给信息,是这个鞋帽部的营业额是六点二万元,他占百分之二十,这个百分之二十就是部分量所占单位的分率。这里这个六点二万元就是一个部分量就有 六点二,除以百分之二十就等于三十一,但是是万元, 所以这一个月的营业额三十一万元。但是我们要求加电部的就用单位一三十一乘以加电部,比如部分量所占的分率 百分之四百二十,也就等于十三点零二 万元。所以家电部这个也这个月的营业额是十三点零二元,十三点零二万元。答, 家电部这个月的 营业额是 十三点零二万元。打家电部这个月的营业额是十三点零二万元。
5小孔同学 02:30查看AI文稿AI文稿
02:30查看AI文稿AI文稿六年级上学期呢,期末考试一定会考这一类扇形的统计图,来看一下这个例题。六年级的某一个班,统计了一下他们喜欢的 体育运动有哪些,其中呢,喜欢排球有百分之十八,篮球有百分之十九,喜欢足球的这里没有直接告诉我们,但是呢,从这里是个九十度,你可以推出它其实是四分之一, 大家都写成百分比,那四分之一写成百分比呢,是百分之二十五。上面这里呢,乒乓球的也没有告诉我们,我们可以用 一半减去排球的百分比,也就是百分之五十减去百分之十八,你也可以用 百分之百减掉其他这四部分,算出乒乓球的占比是多少,那我们就把五类体育运动的百分比全部都算出来了。来看第一题,喜欢足球的有十五人,让我们算一下全班总共有多少人。用全班的人数去乘以这一类 球类的百分比,就可以算出这种球类喜欢的人数有多少。所以呢,我们的足球也用同样的方法,全班的人数不知道,那他可以用足球所占的人数是十五人, 去除以足球所占的百分比是百分之二十五,算出了全班的同学一共有六十人。 这一类也属于用题呢,记得要有一个答语答,全班有六十人。第二题, 那我们找一下最受欢迎的两种运动是什么运动,他们的百分比之合呢?有多少?在扇形统计图里面所占的百分比越大,说明喜欢的人就越多。乒乓球我们先算出来是一减去百分之十八, 算出来乒乓球的占比是百分之三十二,乒乓球所占的百分之三十二和足球占的百分之二十五是最多的,说明最受欢迎的两项运动就是乒乓球和足球, 那他们所占的百分比有多少呢?乒乓球是百分之三十二,足球是百分之二十五, 我们把这两部分加在一起,可以算出来它是百分之五十七。最后把我们这一类应用题的答语也给他写出来,那么这个题我们就完成了。
119蔡蔡老师数学分享






