合肥一模化学卷标准答案
粉丝7.2万获赞44.1万
相关视频
 00:27
00:27 01:41查看AI文稿AI文稿
01:41查看AI文稿AI文稿合肥一模今天刚结束啊,我认为还是有难度的,像刚刚结束这个数学啊,挺难的,计算量也比较大,于是最后一道题的最后一问,估计很多同学都写不出来啊。再说下来,先从第一天开始说这个语文, 嗯,我认为也比较有难度啊,挺抽象的,所以说就是语文基础不太好的话,可能做起来也不是特别简单。嗯,再说一下这个理科啊,物理,我认为物理啊,物理还是挺简单的啊,就相当于送分的。 嗯,生物和化学呢,你像这个生物难度不大,但都是基础化学可能就是有点计算量偏大一点。 这是理科啊,然后这个文科啊,文科,然后我认为他的难度系数要比理科的难度系数大,就是小两门啊,我认为还是挺难的。 你像英语吧,英语的生词还是,呃,比较多,我认为英语还是有难度。对,就是有阅读理解 c 篇和 d 篇啊,包括七选五 啊,生字比较多。听力吧,听力的话,呃,前面还好,后面的话就上强度了。所以说我认为这个英语也有点难度,但是没有像这个省时,还有这个江淮学校那个英语那么难啊。这是整个这个合肥一模的卷子啊, 这个卷子不错,大家呢,如果想做的话,那个拿回去下载打印,我给大家整理好了,电子版包括打印解析都有,趁着这个寒假去做一做,看看我们哪哪里有这个弱点,抓紧去补啊。其实一模最主要就是查缺补漏 啊,查缺补漏,不要去在乎这个分数啊,但到时候大家可以看看我们的校排名吧。
159皖北教育圈~星途李不开 00:26查看AI文稿AI文稿
00:26查看AI文稿AI文稿咱们安徽高三合肥一模这两天的考试已经结束了,整体来说呢,还是有难度的,除了物理,相对于其他科目是比较容易的,等于送分了。语文呢,作文零点,人生还是比较抽象的,数学的计算量也比较大。 我这里整理好了合肥一模的试卷,还有答案解析,如果有想对答案的可以给我发信息。
32安徽星途朱老师 01:10查看AI文稿AI文稿
01:10查看AI文稿AI文稿咱们合肥一模上午已经结束了啊,语文和化学,先说下这个难度,语文还是有难度的啊,无论是我们这个阅读理解,包括我们这个语言文字运用, 乃至我们这个最后一题,这个作文啊,写的是零度人生,嗯,都是有的难度,像这个作文如果你基础不太好的话,写起来还是挺困难的啊。化学呢?我认为就,嗯,很常规吧啊, 不是特别难,但考验的都是基础。其实这个一轮,这个这个一模啊,主要就是检测你在一轮的复习过程中有没有夯实你的基础。那如果考的不是特别好的话,那接下来我们从一轮啊到二轮之间, 你该如何调整方向,对吧?其实一模就是查缺补漏啊,所以说那个大家一定要趁这个寒假好好去找找你的弱点, 然后没有考这个,这个我们合肥这个一模这个考试的想做卷子的啊,然后给大家整理出来,然后拿回去下载打印去做一做合肥一模很有参考性,大家都懂的。
145皖北教育圈~星途李不开 02:23查看AI文稿AI文稿
02:23查看AI文稿AI文稿怎么说呢,今天也是刚考完那个和平精英啊,考三科,然后完了之后我太想念,太想对答案了,我说我要答案了,在小红书上找答案,也不知道,也不知道,也不靠不靠谱啊,我先对一下啊,好紧张啊, 我跟你说,我考我考这三科之前我都虔诚的拜了一拜,拜拜。哎呦,我这么勤奋爱笑的女孩运气一般,一般都不会太差啊,我看对了, a, b, c, b, c 哈哈哈哈哈哈,什么?哈哈, dc 出现了 a, b, 啊,这不可能吧,答案不错了,哎呀,对吧对吧! c, e, t 啊,这个前面太棒了,太棒了! dc, 我靠,这里面有哪些狗屎? b, b, b, b。 好, 可以破一个圆形的,这种破几个?这几个破太多了,我就说一个两个三个四个, 总共多了一二三四五六七八九十,哈哈哈哈! next 倒计时了啊, a, a, b, b, b 哈哈哈! b, c, d, b, c, d, c, d, d, a, c, d, d, a, c, d, d, a, c, d 这个小姐, c 哈哈哈,一个两个,三个四个五个, ok, ok, 我 可以接受,但他妈还是吐好多呀我,现在,我现在是不是想哭 哈哈哈。 d, a, d, a 哈哈哈哈,哎呀妈,记错了, d, a, d, a, d, a, d, a, d, a, d, a, d, a, d, a, d, a, d, a, d, a, d, a, d, a, d, a 哈哈哈, 嗯,行不行?一个两个三个四个五个,哎呦妈呀,哎呦,我受不了了。
682xxoie_xx^ 00:26查看AI文稿AI文稿
00:26查看AI文稿AI文稿大家通报一则消息,那么合肥市的有关部门已经公布了二六年的合肥一模的均分,那么除了语数外这种科目之外,小三们当中赋分的两科已经赋分完成, 那么这个均分是赋分后的分值。由于合肥市不公布特供线和本科线,所以请大家关注老师的预测。
138钞老师聊升学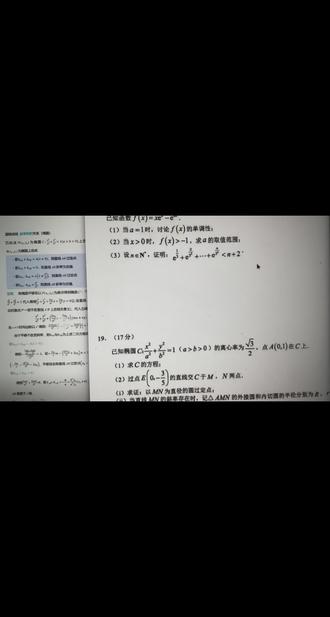 01:44查看AI文稿AI文稿
01:44查看AI文稿AI文稿我们来看一下最近这个合肥一模的压轴题,这个第二问的第一小问,求 m n 为直径的圆过定点,那这个定点它你直接算是很难算的, 一般我们就先简单先做最简单的情况,那就是什么呢? m n 平行于 x 轴,就是水平的一条线的时候,你找圆的,找圆上的点,很好找,对不对?你这个时候你发现这个手以 m n 为直径的圆,正好过这个 a 点, 过这个 a 点啊,也就说过椭圆上的这个上顶点,那既然过椭圆上上顶点,那你就应该想就是,那你猜大概大概率,也就是这个 a 点,也就是定点了啊, 这就是由特殊到一般的思想里面,你得大胆的猜,然后你既然有这个猜测了,那你自然联想到这个 原值曲线里面斜率合集关系,这是我之前发的一个视频,去年就发的。然后这个第三点,你看这个 p 点就是原上的一个椭圆上的一个点, 那你这边就相当于是斜率至极,等于负一为定值,因为是圆嘛,对吧?斜率负一为定值,那对应的直线 a b 过定点,就对应这个题里面的 这个题里面 m n 过 e 点,对吧?实际上把这个结论但凡记住了,过定点反推过来就很好反推了。
27北顾. 03:15查看AI文稿AI文稿
03:15查看AI文稿AI文稿先来对下这个物理单,刚对完这个三十四分的化学,这个在物理上面找点安慰,因为他们说这次物理非常简单,我觉得比之前的真的是简单好多好多。 他说对 a d c d a d c d。 可以 可以可以, c b c b b c b b, 我 靠,单选就错一个, 创造历史,创造历史,然后 b c a c d b c a, 我 靠,把自己排了是干嘛呀? 这。我选的 a d, 那 就是那就是这个。呃, a, c, d, 选了两个,错了一个 c, 选不全,得三分就扣两分,减两分,加上四分,六分,谁一辈子?算了算了算了,这次太简单了,真的没办法。 f 呀,方向大小 f 啊,是 f 吗?还是看不清楚啊?是 f 吧, 后面标点符号是 f, 然后 c 错了。我写的是一直减小啊,不是,写的是 a 六,最大八十九啊。我答题卡上应该没加零,因为我感觉不对劲,二点七,一点,哎。啊,一点四差不多,二点七,一点四差不多吧。对,所以说我这个实验题也是只错了一个。扣个两分吧,行不行?扣个两分 好,再来对大对,大题零点五我也不确定,好像是对的吧。零点五应该是的,我觉得是二分之一吧。应该是的哈,七十五,哎,等会 七十五吗? f 等于七十五吗?哦,对对对,在这在这,可以可以可以,这题满分吧,说实话,算了,不扣分了,给自己一个鼓励吧。满分,然后第二题呢? 第二题一百牛吗?一百牛,好像是的吧,我不记得了呀。哎,我打底卡, 我靠,完了,这里错了一个大小和方向,然后这个算了,扣个三分吧,行不行?这个的话是扣个六分,这对的减零分,这个, 呃,一百牛。对的,第二小题是两千克。对的,第三小题是一千二百牛。减零分。可以可以,最不糖的一次。然后第三大题二 m v 零方比上 q l。 对的对的,可以,可以。最后,嗯,第二小题是 l 三 l。 对, 对,这题不会啊。嗯,减个多少分呢?这多少分?第三小题一共是三三四四四五七分。减个七分吧, 加七是七分,所以七加上这个三十十六分。我靠,这物理一共就扣十六分。我靠,是最好的一次啊,也就是说考个八十四分,对吗?我靠,这谁一辈子?哈哈哈哈。
386少女严冬 00:46查看AI文稿AI文稿
00:46查看AI文稿AI文稿合肥的一模已经正式考试结束了,根据同学们和老师们的反馈情况来看,合肥一模今年的总体难度实际上是适中的,化生的难度其实并不大,对于学霸来说, 考到九十五或一百分还是比较轻松的。数学的试卷尤其最后一题,体现了高考数学的风格,很多同学在最后一问上做出来还是比较困难和吃力的。 结合全省一模考试试卷的情况来看,全省一模试卷的难度和水平总体来说是适中的,大部分的特空线都处在四百六到四百九的分数段。 目前我们已经把相应地市的联考试卷和一模试卷上传到了网站上,欢迎大家和老师联系。
32钞老师聊升学 01:15查看AI文稿AI文稿
01:15查看AI文稿AI文稿合肥高三一模已经结束了哈,先说一下这个难度,语文呢,还是有点难度的,无论是我们这个阅读理解,包括我们这个语言文字运用,乃至于我们最后这一题,这个作文写的是零度,人生都是有难度的, 像这个作文,如果说你基础不是特别好的话,写起来还是挺费劲,挺困难的。化学呢哈,我认为就是比较偏常规吧,不是特别难考的呢,都是一些基础。 这个一模哈,主要就是检测你在这一轮的复习过程中有没有夯实你的基础, 但如果说考的不是特别好的话,也不用特别的灰心,那接下来应该从一轮到二轮之间,你该如何的去调整方向对吗?这就是咱们考试的秘密。那其实一模哈就是查漏不缺, 所以说大家一定要趁着这个寒假好好的去找一找你的弱点,中考高考看合肥,这个不用说,大家都懂,懂的都懂哈,这套卷子还是非常有价值,去看一看,拿回去让孩子刷一刷的 卷子我已经拿到了哈,想让孩子看看真题的和我说一声哈,不要钱。合肥一模的试卷很有参考性,高一高二高三的真题试卷哈,咱们都有,想看题的和我说一声,加油!
 43:12查看AI文稿AI文稿
43:12查看AI文稿AI文稿哈喽,大家好,今天给大家讲合肥一模这张试卷,这张试卷难度比较适中,题型也都比较常规,对于刚一轮复习完的同学们来说,是一张不错的练习试卷。 一题已知集合 a, 集合 b, 那 我们可以先把集合 b 的 一个二次不等式解一下,那解出来就应该是二到五,所以我们 a 交 b, 就 应该是三到五选 c。 第二题,我们可以先把这边展开,展开之后就是一个五加 i, 那我们 a 就是 五, b 就是 一,所以我们五减一等于四选 d。 第三题,我们先看充分性 abc 三点共线是直线共面的一个什么条件?就是它是否能推出来。我们先来看在一个平面内有共线的三个点 abc, 那我们这三条直线是不是只需要过就行了?那是不是他可以随便画?比如说我这里画一条,我这里画一条,我这边这样画一条,对吧?所以很明显我们的 abc 三点共线是推不出直线 abc 共面的,那相反,如果我们三点共呃,这个三条线共面呢? 那是不是因为我这三个直线共面了之后,我这两个平面之内只有一个交线,它交线只有这一条,它交线只有这条的话,所以我如果它这个平面内的直线要与另一个平面相交,是不是这个交点一定在交线上? 那所以我们这交点全在交线上,那是不是就可以说明这三个点是共线的?所以我们必要性是成立的,所以是必要不充分条件。第四题,平均数,平均数全部加起来除以五十,算一下应该是四六四零 中位数,应该看第二十五个和二十六个除以二,对吧?因为现在是五十名员工,所以说我们第二十五个、二十六个全是四千四,所以 我们第二十五个、二十六个都是四千四,所以我们中位数四千四,重数呢?最多的四千四,所以我们 a 大 于 b 等于 c 选 b。 第五题, 两条渐近线,那两条渐近线分别是 y 等于正负 a 分 之 b x, 我 们把 y 等于二代去,就可以得到 x, 但是等于正负 b 分 之二 a 的, 对吧?我们把这两个点的横坐标解出来了,那解出来之后,因为他们动作表相同,所以他们的距离又是横坐标之差,所以这个等于二应该什么? 是不是应该是我们 b 分 之四 a 两式相减, b 分 之二, a 减 b 分 之负二, a 等于二,所以我们就有二 a 是 等于 b 的, 我们进一步 c 就 等于根号五 a, 所以你先列根号五。第六题,他被偶函数则犯了最小之位。前面这个是我们熟知的奇函数,对吧?我们带一个负 x, 就 应该长这个样子, 然后给他上下同乘二的 x 次方, 那是不多一个符号啊。那前面就是奇函数,我们要整体是个偶函数,是不是我们后面这个必须是一个奇函数, 那么 cosine 是 个什么? cosine 是 个偶函数,对吧? sine 才是奇函数,所以我们应该把后面这个东西让它变成 sine 就 可以了,对吧?那我们说既变偶不变符号,看象限,所以我们 sine 减六分之 pi 就必须是一个二分之差的奇数倍,因为这样的话,我们才可以变成三,也成为一个奇函数。那奇函数乘奇函数就是一个偶函数,所以就这样。那我们 k 属于 z, 我 们看翻译大于零的时候,最小值应该是多少?最小值应该是我们 k 取零的时候,对吧? k 取零的时候,我们翻译是个三分之二,所以选 c。 第七题,它要求 a 在 b 之前, c 与 d 的 时候,对吧? k 取零的时候,我们翻译成三分之二,所以选 c。 第七题,它要求 a 在 b 之前, c 与 d 的 时候,我们翻译成三分之二,所以选 c。 第七题,它要求 a 在 b 之前, c 之前, c 与 d 的 三分之二,所以选 c。 第七题,它要求 a, 它要求 a 在 b。 我 们不太好 直接翻译,那我们可以稍微来看一看情况。那 c 和 d 相邻,我们是不是首先有 c、 d、 d、 c 两种组合,也就是我们这里有两种组合。然后呢,我们现在把它捆绑之后,我们把它看做一个新的,比如说 f 从现在就是 a、 b、 e、 f 四个在排,然后 a 在 b 之前,如果我 a 在 第一个,我们后面三个是不是随便排? a 一定在 b 之前,所以 a 三三。如果 a 在 第二个, 那是不是我们 b 必须在后面两个,然后前面必须是 e 和 f 的 其中一个,所以我们这里 c 二幺,把 e、 f 选出来,后面 a 二二随便排。那如果 a 在 第三个,前面有两个, 那是不是 b 必须在后面这一个呀?那前面这两个是不是 e 和 f 随便排? a 二二,所以这里六种,这里四种,这两种总共十二种, 再加上我们的这个捆绑有两种,所以再乘以二,整个就是二十四种,所以选 b 选项来看。第八题,已知函数 f x 等于洛弦 x 平方加 a 倍, x 乘上洛弦 x 减 x 方,有且仅有三个零点,则 a 的 指数范围是, 那么怎么来分析呢?首先你看到只有一堆洛弦 x 平方,还有个 x 平方,首先是 x 乘洛弦 x, 其实我们稍微换个角度想,如果你把洛弦 x 看成 y, 那 它是 y 方加 a x y 减 x 方这形式,那你会想到什么? 我们会看到这些都是二次的,所以我们会想到一个很重要东西,叫什么?是不是叫其次化呀?对吧? 我们这个东西有零点,那是不是我们可以同时除以 x 方或同时除以 y 方,使它变成一个 y 除上 x 的 一个形式,对吧?那在我们这里不妨同时除以 x 方,所以它有三个零点又等于什么?等价于 lo in x 除上 x 的 平方加上 a 倍, lo in x 除上 x 减一,等于零有三个根,对吧?那我们这个是不是就是一个复合函数零点问题?我们内层函数 f x 就 等于 x 分 之零 x, 外层函数 g x 就 等于 x 方加 a x 减一,对吧?那么先来分析下这两个函数。 首先我们内层函数长这个样子,这个就不多说了, 我们的外次函数呢,我们算算 delta 等于 a 方加四,那肯定是有两个根的, 所以就长这个样子, 这是我们的外次函数。 那由于我们要三个零点,那我们外次函数有两个根了,不妨记作这个。呃,我们拎这个等于 t 吧, ln x 除上 x 等于 t, 那么解出来这个 t 一 t 二啊,它应该在什么样的一个区间里面呢? 我们看我们需要三个,对吧?那我们是不是其中一个?比如说 t 一 小的,我们不妨小的时候是 t 一, 那 t 一 是不是应该属于富穷到零? 应该是 b 选项, t 二数一个零到一分之一就可以,这是一种情况,对吧?因为 t 在 下面有一个根, t 二在这里就会出现两个根,总共三个根,对吧?那第二种情况,是不是我们 t 二属于零到一分之一, 那么我们 t 一 属于零到一分之一, t 二是等于一分之一的,这样的话是不是刚好也是两个加一个等于三个,那么看有没有可能呢?所以我们将分析下外层函数,这是我们内层数应该有的情况, 那 y 函数 g x 等于 x 方加 a x 减一,那么就发现我们的 g 零 一定是小于零的,对吧?所以是不是我们的这个 t 一 t 二它分别在两边啊?证明 t 一 必然小于零, t 二必然大于零,那是不是我们第二种情况就排除了?只有第一种情况,就是这种情况的时候,我们是可以满足他有三个零点的,那他有三个零点,我们 t 已经满足了,我们 t 必然小于零,那么只需要 t 二控制在零到一分之一里面就可以了吧。 那么说记零是小于零的,那现在还需要什么?是不是还需要我们记一分之一大于零就好了,对吧?那么带进去就是一方分之一加上一分之 a 减一大于零,那我们同时乘以 e, 那 a 就 应该大于 e 减一分之一,所以选择我们的 c 选项。这道题我们可以画竖轴分析,也可以画我们的这个绝对值函数图像分析,画一个图像吧,我们这是绝对值 x 减一,这个图像, 我们 a 呢,大概就在这两个点其中之一,然后下一个是我们的 c, 因为我们这个函数值是越来越小的嘛,所以下面还有个 b, 我们就来看我们这些能取哪些值啊?首先你 a 是 最小的那个 a, 这两个点取一个,你如果取右边的 a 是 不是最大的?所以说 a 是 不是只能取左边这个,所以就是我们的 a, 那 c 呢?我们说 c 是 最大的 c, 如果在这里,这里如果是 c, 那 是不是这两个 b 都会比 c 大? 所以我们 c 要当最大的,你 c 只能取右边,所以我们 b 就 这两个点之间夹一个都可以, b 一 b 二,这两个都是可以的。然后我们这里是 e, 我们来看看选项, a 小 于一,对了, a 必须在左边, b 大 于一不对, b 有 两个点, c, a, c 小 于一,那我们就来看 a 和 c 的 关系, 我们现在是不是知道 a 它在左边了,所以我们就开出来一减 a, 它是不是大于我们 c 减一,因为 c 在 右边,所以我们是不是有 a 加 c 是 小于二的,对吧?那我们再由基本公式传递一下 a, c 小 于一就没有问题。 我们来看 d 选项,如果我 b 在 右边就是我们 b 二,那是不是 b, c 肯定大于一,因为你 b 也大于一, c 也大于一,如果 b 在 左边呢? b 在 左边的话,我们这个不等式是不是变成了 c 减一大于一减 b, 对 吧?我们就会有 b 加 c 大 于二,那 b 加 c 大 于二,一定能推出来 b, c 大 于一吗?不一定啊,对吧? 比如说一个我们取二,一个取一个三分之一,那你乘起来不是三分之二吗?对吧?所以说它不一定大于一,我们由不等式创造拨序反号了,所以说 d 不 对,所以第九题选 a, c, 再来看第十题, 第十题,这两个乘积等于四,那我们知道 f x 等于三, omega x 加三分之派,它的取的范围是不是负一到一?那你要乘积等于四的话,是不是这两个都只能等于一才行,对吧?所以说 a 是 对的, b 选项,若 x 一 减 x 绝对值,最小值为 pi, 则 omega 等于一,那 x 一 减 x 绝对值是不是就就是我们的一个周期,或者说就是它周期的一个倍数?因为我们看,因为我们都是这个极大值点, 那是不是极大值点跟极大值点之间相差了我们周期个单位,对吧?那当然你也可以是其他极大值点,比如说这个极大值点,那就相差两个周期,那最小值就是我们的一个周期,对吧?所以说一个周期就是二, pi 除以 omega 等于派,那 omega 等于二,所以 b 不 对。我们大家看 c, 若 x 一 x 二属于零到派,则 omega 取值范围,也就是说我们在零到派里面一定要干嘛? 一定要有两个极大之点,对吧?那么极大之点怎么写的?极大之点是不是我们的 omega, x 加上三分之派等于二 k 派啊?加上我们的周期,然后 k 除以 z, 我们要在这个里面至少有两个极大之点,所以我们就来看我们是哪两个。第一个的话肯定是等于二分之派,第二个的话是不是这边 k 取一,那是 omega x, 我 们算一下,等于六分之十三派, 这是我们的第二个极大之点,就是说我们 k 取一的时候,那这个极大之点一定要在我们的零到派里面。我们现在 x 是 属于零到派,那么我们 omega 能取什么? 我们欧米伽是不是最小?最小的是六分之十三?因为在六分之十三的时候,我们是不是 x 取 pi 的 时候,我们刚好是六分之十三? pi, 如果你比六分之十三还小,那我们这两个乘积是不是一定比六分之十三 pi 要小?所以说我们最后这个值是不是一定不会在这个里面,对吧?我们这里面就不会有两个其他值点,对吧? 所以 c 是 没有问题的,六分之十三倒置无穷, d 这个的最大值为欧米伽 分之四派,那是什么意思呢?我们刚才才说过,我们这两个之间的差值是不是周期的一个倍数?周期的整数倍?那我们一个周期叫欧米伽分之二派,那欧米伽分之四派是不是代表两个周期? 也就是说我这个里面至少包含了极大值两个周期,那是什么意思呢?我们来看一看, 我们不妨画一下。所以说就说我们的第三个极大之点是不是也必须在里面,我才会有 omega 分 之四派出现,因为这样的话,我们这里才是两个周期 omega 分 之四派,对吧? 那第三个极大之点在里面,由于它是最大的,也就说我这里面不能比它更大了。如果我有四个极大之点在里面,那我最大是不是可以间隔三个周期?那三个周期是不是 omega 分 之六派? 所以说欧米伽分之四又限制了你必须有三个知识点,就是极大知识点在里面,但是你不能有四个极大知识点在里面,因为有四个的话,你就间隔了三个周期是可以的。所以说我们看一看第三个极大知识点,什么第三个极大知识点在这个基础上再加二拍,那就是一个六分之二十五拍, 那第四个极大值点再加二派就是六分之三十七派,那我们说第四个极大值点不能有,所以说我们这边你 x 属于零到派嘛,我们现在把派约掉,所以这边是 b, 这边是开,对吧? 还是一样的,你 x 属于零到派,如果你的 omega 小 于六分之二十五的话,那你乘起来就不可能得到一个六分之二十五派。相反,如果你 omega 大 于等于六分之二十五的话,那你就存在一个 x 属于零到派,使得你俩乘起来是一个六分之二十五派,那这面是同理的, 所以我们知道 omega 的 指数范围,六分之二十五到六分之三十七左 b 右开,所以 d 选项是正确的。 一题十一题,我们这个是一个老结论题了,就是说我们这个过焦点 f, 然后这个 x 等于负一,这个直线是他准线吗?那我们过他直线,然后做的这个垂线呢?我们这个 a、 o、 n 一定是共线的, b、 o m 也一定是共线的,这都是老结论了,对吧? 我们看 a 选项证明向量 o a 平行向量 o a, 那 我们知道向量的平行跟共线其实是一样的,所以我们只需要证明 a、 o、 n 共线就可以了,那这个就非常好,知道就留给你们自己证吧。不管是射线还是射点,你最后把 a 点跟 n 点的坐标表示出来,我们去算 k o a 和 k o n 的 斜率,它就是一样的 变向,若 m f 等于 m a, 则 o m 等于 m f, 在 这里它等于我们 m a, 我 们 m a 呢?又等于我们的 af, 对 吧?所以说就是一个等边三角形,等边三角形,这里是六十度,六十度的话,这里垂直,这边就是个三十度, 对吧?那这里是三十度,我们知道底下这里是二,那我们这段长度是不是一个二倍?根号三,那么 o m o m 是 不是再加上这里,这里是一,所以我们 o m 是 不是根号十三没有问题, c 选项则直线 a b 的 斜率为幺三。那我们知道了你的这两个共线之后,你的这个叫 a o n 共线之后,我们这个 a o 等于二倍的 o n 是 不是可以转成我们的横坐标? 这一段是不是等于二倍的?它那么知道这边是一,这边是不是就应该是二?这边是二,我们又有 o f 是 不是一,所以这段是不是一,对吧?这段是一,我们整个这个长的是不是三?这是三的话,我们 a f a m 相等,是不是也是三? 那我们由勾股定律,我们这条边是不是二倍根号二,所以我们的 k 是 不等于二倍根号二的,对吧?所以不等于根号三,所以我们 c 不 对。 d 选项三角形 a b n 面积最小值,那你不管是设点设限都可以最后化成一个单位量函数求导算最小值就好了,最后算出来是正确的,没有问题的。这里需要提醒下,就是说你如果是设点的话,你的 b 的 纵坐标,你记得它是一个负数,你在算这些面积的时候记得加一个 呃,绝对值,或者说你加一个符号, ok, 这是我们的十一题填空题部分,十二题已知等差数列满足这样一个式子。那我们知道 a 三是不是等于一个二,加上二 d, 我 们的 a 二呢?等于一个二,加上 d, 所以 我们就可以把 d 解出来等于负四,所以我们的括号式就是负四 n 加六十三题,我们先画一画圆台, 告诉我们上里面半径为一,下里面半径为二,母线长为根号五。然后呢,告诉我们这个上下底面的圆周均在同一个球的球面上,那是不是我们这个球的球心肯定在这条直线上,对吧? 那我们不妨把这里设为它的球心角 o, 所以 我们就利用它到上里面的圆周的距离相等来建立方程,算出来我们的 r, 那 就是我们的 r, 那我们算之前,我们是不是需要知道我们的高是多少啊?那我们母线是长,是根号五,那这里做一条垂线下来,这边是一,这边是不是二,对吧?所以我们的高是不是二?高是二的话,我们不妨设这边为 x, 这边是一个二减 x, 所以 我们就会有一的平方,加上 x 的 平方是等于二,加上二减 x 的 平方,对吧?我们解下这个方程,可以解出来 x 等于四分之七, 于是我们的 r 就 等于多少呢?或者我们的 r 方就等于我们的十六分之四十九加一一的平方加 x 的 平方嘛,等于十六分之 六十五,我们的表面积呢?是不是四 pi r 方,所以就是我们的四分之六十五 pi, ok, 这我们十三题来看,十四题已知直线 l 与我们的这个曲线 y 等于 x 方减为 x, 然后满足这样的一些关系式,让我们求这数量积的最小值, 那么知道求数量积的话,如果它的对边是固定的,我们现在 pm 点成 p n, 对 吧?我们 m n 是 固定的,那我们一般采用什么方式呢?我们一般是不是采用极化恒等式的方式?比如说我在这里先画一个 p 出来, 因为我们对边固定下来之后,我们只需要算我们的这个点,到我们对边中点的这个中线长就可以了。也就说我们用极化函数 p m 点乘 p n, 就 会等于我们 p h 的 平方减掉一个我们 h m 的 平方,那等于我们 p h 的 平方 减二,对吧?所以我们就要来算这个 p h 的 平方的最小值, ok, 那 p 怎么来的? a 又在动, b 又在动,生成了一个 p, 那 这种多变量问题,我们一直在强调一个思路,叫什么?是不是主元的思想。不管在立体几何里面有两个动点,还是说我们的这个导数里面两个变量, 我们遇到多变量问题,如果不能整体换元的话,就是比如说你既有 x 又有 y, 但是我们可以把 x 加 y 看作一个整体,之后就成个单变量的一个函数,如果不能这样做的话,一般都是一个主元的思想,也就是说我们先控制一个,比如说我们现在 a 不 动,我们 a 就 在这里, 那靠我们 b 怎么动的时候,我们 p h 取最小,因为我们现在 a 不 动了,对吧?相当于 a 是 一个定点, a 是 一个定点的话,我们又有 ap 等于三倍的 pb, 那 是不是我们就知道 p 的 轨迹肯定是一条平行于这个 b 的 轨迹的一条直线,并且是一个, 这边是一个三比一的一个关系。 ok, 那 我们看 p 在 这个直线 l 撇上面动的时候,什么时候最小?那是不是垂直的时候? 也就是说我们在这里有一点 p 一 撇,那就是我们在 a 固定的时候, p 一 撇这里,我们这个 p 一 撇就可以取最小值,那么此时 b 在 哪里? b 是 不是在这里?所以我们知道最小的时候是垂直了,所以其实我们要求了什么?我们发现这里是不是很有一个三比一的关系,那是不是这里又是垂直? 所以我们实际上算的是不是就是我们 a 到这个直线的这个距离的最小值就可以了?把这个最小值算出来,我们再乘以四分之一,是不是就是我们这一段了? 那这一段是不是我们最小了?所以说我们一直在强调有多变量的话,一定考虑主元先定一个动一个,先解决掉其中一个,再去解决另一个。我们这里先把 a 确定下来,然后去解决 b, 那 确定 a 确定下来之后,就有这样一个 b, 然后在这个时候我们这个 ph 取最小,那么再去动 a, 使得 在 a 在 什么情况下我们这个 ph 最小就可以了。所以我们知道我们现在要算的就是我们的这个曲线上的一点 a 到我们这直线的距离的最小值,对吧?所以不妨 a 就是 x 零 x 零的平方,减零 x 零, 那么这个距离就可以写出来,就是根号二分之 x 零减 x 零的平方加上 loi x 零加二,所以我们就需要算这个 x 减 x 平方加 loi x 的 最小值,对吧?我们求个导,它等于一减上二 x 加上 x 分 之一,很明显它在 x 等于一除以最小值, 所以我们来算一算 f 一, f 一 就等于零,对吧?那 f 一 等于零的话,我们这个式子的最小值 是不是就等于根号二,那它等于根号二,我们这段 p h 是 不是它的一个四分之一,所以我们这段是不是四分之?根号二, 那么最小值是 p h 的 平方减二,那它平方是不是八分之一?所以八分之一减二等于多少?等于负的八分之十五,对吧?所以最小值就是负的八分之十五。 数题已知,这个式子让我们证明 a 方等于 b 方加二 c 方,那么知道可算 b 加 c 是 不是等于负的可算 a 的 呀?咱们就有 c 加上二 b, 可算 a 等于零。那么看到证明一个全是边的式子,我们是不是想到肯定是可算 a, 写成一个什么 二 b, c 分 之 b 方加 c 方减 a 方,给它带成边,对吧?所以我们带进去就会有 c 加上 二 b 和二 b 约掉 c 分 之 b 方加 c 方减 a 方等于零。两边同时再同时乘一个 c, 我 们就会有 a 方等于 b 方加二 c 方,这我们第一问,第二问,让我们求这个 c 的 最大值, 那我们知道我们现在都是边的关系,所以我们求 c 的 最大值的话,我们应该用余弦,对吧?因为现在只有边,所以我们口算 c 就 等于 二 a, b 分 之 a 方加 b 方减 c 方,我们上因为有边的关系,我们这里下面又是 a b, 上面又是 a 方加 b 方减 c 方,所以我们想就是把这 c 方看能不能用 a 方和 b 方代掉,代掉的话最后剩一个其次式,不管你用基本公式还是其次化都是可以的,对吧?它又等于二 a b, 我们把这个 c 方代掉,上面就剩二分之一 a 方加上二分之三 b 方,那么分子是不是大于等于我们的二乘上二分之根号三 ab, 然后底下是二 ab, 这就等于二分之杠三,或者你这里奇次化也是可以的。我们是不是整体这个口袋 c 就 会大于等于二分之杠三,那口袋 c 将大于等于二分之杠三,我们 c 是 不是小于等于六分之派,对吧? 那么算一算去,等,那是这两个相等的时候,也就是我们 a 等于根号三 b 的 时候,我们这个火灾 c 就 刚好等于二分之根号三,所以我们 c 就 取最大值六分之派。 ok, 这门数题 第一问,第一问是一个超几何分布问题,我们直接写就可以。 p x 等于零,就等于 c 五三,然后 c 三零, c 啊, c 二零,黄球取零个,然后 c 三三就等于十分之一, p x 等于一就等于,还是 c 五三上面呢?需要取一个黄球,所以 c 二幺 c 三二就等于五分之三, p x 等于二,就等于 c 五三分之黄球两个全取 c 二二,然后 c 三幺,取个白球就等于十分之三, 所以我们整个分布列就可以写出来, x p 一 呃零一二十分之一,五分之三,十分之三,所以我们就可以把期望写出来,就是一个五分之六。 第二个在取球过程中已取出的白球个数始终不小于黄球的个数,那这个是不是很像我们之前讲过的卡特兰数的一个取法呀?所以说我们这里直接因为只有五个嘛,所以我们就每举一下有哪几种情况就可以了。第一个是不是只能取白球? 因为第一个取黄球的话,你黄球上来就比白球更多了,对吧?那么第二步呢?是不是可以取白,也可以取黄? 那你注意啊,我们这个口袋里面只有两个黄球,所以我取了两个白球之后,剩下什怎么取都可以,对吧?因为剩下我再怎么取,最多也就取出来两个黄球, 那是不是始终就这个白球都是不小于黄球的?那下面这种情况呢?那是不是我还有可能取白是可以的,那这个我们说取了两个白球也可以了,然后接下来,然后如果他取黄呢?是不是不行?所以说我们这边是不是也只有这一条路,也就说取我们的白球, 所以说我们总共的情况是不是就这两种,白白或者白黄白,对吧?我们算一下概率,第一个取白球是五分之三,第二次取白球是二分之一,第二次取黄球是二分之一,取了黄球之后再取白球是三分之二,所以整体就是一个五分之三 乘上一个二分之一,加上二分之一乘三分之二,整体就等于二分之一。 ok, 这我们的十六题我们来看十七题。第一问,让我们证明 m n 平行于平面, b c e 这里这里看着 m n 很 像终点,就你这个 e n a 连过来,甚至是共线的, 但你千万别被他骗了,就说我们知道这两个长度相等,但是并不知道他是否是终点。 ok, 来看一看题目值,三棱柱,那就说侧面都是垂直的,然后所有的它都等于二,那要是侧面都是正方形,对吧?然后上下都是一个正三角形,对吧? 所以说我们不妨令这个 c m 等于 x, 这边是不是 x, 那 么你想想怎么正呢?现在既然他不是 这个 a n e 共线,也就说我们 m n 都不是终点,他有可能画成这样,那么怎么正呢?那我们是不是要平行于平面 b c e 的 话, 我们是不是得往这边找一条线跟它是平行的呀?咱们就不妨给他做过去一个,这里就称作 m e 撇,这里就称作 n e 撇,做一下平行线, 那我们这个 m a 一 撇, n 一 撇就在我们的这个呃平面 b c e 内了,我们就看它能不能是一个平行四边形。那首先你做平行于里面,做平行于里面,你的这个 m m a 一 撇跟 n n 一 撇肯定是平行的,对吧? 那么看它长度是不是相等的呢?那我们知道你这个是个正方形,你做平行的话,是不是这个也是垂直的?这里也是四十五度,所以说我们这个是不是二分之根号二 x, 这个是不是也同理是二分之根号二 x, 对 吧? 所以说我们这个 m m 一 撇跟我们的 n n 一 撇是相等的,所以平行且相等,它是什么?平行四边形,对吧? 平行四边形的话,那是不是我们这两个线段就平行了?他俩平行的话,那我 m n 是 不是平行于平面 b c e 了,对吧?第二问,若 m n 等于一,那这个等于一,这个等于一,我们就可以利用这个三角形来建立方程,对吧? 因为我们有这边的 x 吗?这边是二分之高二 x, 然后你拿这个再减一下,就是这个东西。所以说我们有这两个之后,我们可以利用这个三角形,因为我们上下底面都是一个正三角形,这里是这个六十度,所以你可以用这个来建方程。建方程之后我们就可以解出来,这些都其实都是终点啊, 这些全部是终点,你现在又都有垂直,所以说怎么办?随便找个点间隙就好了吗?这个间隙并不麻烦呀,底下都是垂直的,对吧? x y z, 比如说 b 点,那你用 a 点什么的也可以啊, z, 对 吧?你接完戏之后,剩下的计算就用你自己算啊,最后算出来是一个七分之一。这个还是一个比较简单的例子,集合看我们的十八题。第一问, 当 a 等于一时讨论 f x 单调性 a 等于一的时候,我们 f x 是 不是等于 x 乘上 e 的 x 方,减上 e 的 x 方?我们求导,就等于 x 乘上 e 的 x 方,所以我们整个 f x 是 不是在 我们负无穷到零到递减,零到正无穷到递增,对吧? ok, 这我们第一位。 第二问,当 x 大 于零时, f x 大 于负一,求 h 的 范围,我们不妨令 g x 就 等于 x 乘以 x 的 平方,减上 e 的 a, x 次方加一,我们需要在 x 大 于零的时候,我们 f x 大 于零的,对吧?哦,我,我们的 g x 大 于零的,对吧? 我们注意到 g 零是等于零的,所以我们可以拿短点效应来做, g 零是等于零的,所以我们的 g 撇零 小于零的话,是不是就会产生矛盾?因为我们需要它大于零,我们现在零在这里,那它小于零是不是出来是往下走的就会矛盾?所以说我们看一看这种情况一, 呃,我们先求导吧,还是 g 撇 x 又等于我们的 x 加一,乘上 e 的 x 四方,减上 a 乘上 e 的 a x 四方,我们的 g 撇零就等于一减 a。 第一种情况,若 a 大 于一,则 g 撇零小于零,于是我们一定存在一个 x 零大于零,使得 我们 g x 在 零到 x 零上到递减,那么此时 g x 就 会小于 g 零等于零,矛盾,对吧?那如果有的省短点效应要求你找点的话,你可以稍微找一下, ok, 那 么第一种情况,第二种情况弱, a 小 一点一, a 小 一点一,我们就要证明它成立,对吧?那我们此时 x 乘上 e 的 x 方减 e 的 a, x 方加一, 它是不是就会大于等于我们的 x 乘上 e 的 x 方,再减到一个 e 的 x 方加一,那再由第一问,它是不是大于等于零的,对吧? 由于我们第一问是在零处去的,我们这里是 x 严格大于零,所以最后改成一个严格大于零,所以就挣完了。这我们第二问,我们来看第三问, 第三问,我们由第二问是不是得到一个不等式叫 x 乘上 e 的 x 方减上,或者是第一问的不等式减上一个 e 的 x 方要大于等于我们的负一,对吧?我们现在需要 e 的 多少东西?所以我们需要把这个 e 的 x 方单拎出来, 说明他是 x 减一,乘上一个 e 的 x 方大于等于负一。由于我们这个指数都是在零到一的范围里面,所以我们这里不妨约束一下, x 属于零到一,那么此就会有 e 的 x 方小于等于 一减 x 分 之一,对吧?包括我之前在讲那个数列导数放松的时候也讲到,你一定要会用前两问去造这个放松, ok, 我 们现在有了这样一个式子, 有了这样一个式子之后,我们就带入这些东西,我们就会有 c 个码,这个啊,这些上下标我就不写了,有点麻烦。 e 的 三的 k 次方分之 k, 它就会严格小于我们的 sigma 一 减上三的 k 次方分之 k 分 之一,对吧?我们就把这个再化简一下,它就会等于 sigma 三的 k 次方减 k 分 之三的 k 次方。我们再给大家分离常数一下,就是 sigma 一 加上三的 k 次方减 k 分 之 k。 于是我们有了这个之后,我们下面就证明我们这个式子 sigma 三的 k 次方减 k 分 之 k, 它要小于二就可以,对吧?因为前面这个一你 c 个码加起来,前面 n 个数码刚好加起来就是 n, 对 吧?所以我们需要证明这个式子, 证明这个式子的话,你一看右边小圆,你就想到这个东西能不能放成个等比初恋呢?或者说有关等比的,比如说一个这个等比分之等差,这种错位相减的形式也可以,对吧?但总而言之,你需要能放成个求和的形式,所以说我们观察这个形式啊, 你要是能放成一个求和的形式,其实主要在哪里?主要在我们这个 k, 对 吧?因为如果这个 k 你 能放掉的话,比如说我们三的 k 次方分之 k, 或者三的 k 减一次方分之 k, 这些我们都是会求和,对吧?所以说你的重点在于这里,那这里我们给他怎么处理一下就能变成 k 求和的形式了呢? 那首先整体是小于号,小于号的话,我们这个底下是大于号,这底下要大于号,我们 k 前面一个负号是不是要 k 这整体 k 需要有小于号,咱们就看 k 小 于什么, 那么就想到前面是三的 k 字方,你只要放的跟它相关,是不是我们就可以求和了?那比如说我直接放三的 k 字方可以吗?这是不可以的呀,因为你这里是不是减号,你就嗯直接减成零了就没有意义了, 所以我们可以尝试一下三的 k 减一次方,这个也可以证明一下它成立了。那三的 k 减一次方的话,我们带进去就是什么这个 c 个码,三的 k 次方减 k 分 之 k 就 会小于 c 个码, 我们把三的 k 减一次方带进去就是二乘上三的 k 减一次方分之 k, 那 这个设置我们进行一个错位相减,它就等于 八分之九减上四分之三,里面是二乘上三的 n 减一次方分之一,加上三的 n 次方分之 n, 那 这个我们说是小于八分之九的, 所以它还是严格小于二的,所以我们第三问就正完了。第三问整体还是利用前两问给出的一个放缩去进行一个放缩,最后再处理一下后面放缩的式子就可以。这个题也整体上难度不大, 我们来看看十九题,这十九题比较简单啊,第一问就不多说了,这个方程呢是四分之 x 方加 y 方等于一,我们来看第二问过点 e 的 这个直线交于 m n 两点。然后第一问,让我们求证 以 m n 为直径的圆过定点。 我们怎么来看这个问题呢?首先 我们由对称性以及我们的中垂线结构就可以得出这个的直径的圆过定点,那这定点一定在 y 轴上,对吧? 这个我们之前在那个对称性那里也讲过。呃,所以在这里就不多讲。所以我们可以由对称性加上我们的中垂线结构得到这个定点,不妨叫做 t t 呢?一定在 y 轴上, 那由于我们是这个以它为直径的圆过定点,所以我们相当于是不是要证明 k tm 乘上 k t n 等于负一, 那斜率乘积是一个定值,是不是我们之前讲的轴点弦顶点角问题啊?轴点弦顶点角是不是就可以出来我们斜率乘积是一个定值,对吧?所以我们就想这个 t 他大概率或者说他只能说我们上顶点了,因为其他点都不可能出来。斜率成绩是一个定值,你这是一个定值线,因为你这是一个轴点线,我们只有顶点角所形成的这两条线的斜率成绩才会是个定值。所以我们只需要验证上顶点 这个与这两个点就是我们的 t m k t m 乘 k t m 是 不是等于负一就可以了?我们只需要验证一下上顶点就可以了。 当然你也可以证明更一般的情况,就说我设一个在 y 上的 t, 对 吧?我设一个在 y 上 t, 然后利用伟大定律表示这个 ktm 乘上 ktm。 最后再说明这个 t 上顶点都是可以的。 你直接验证上顶点,验证完,你把它验证完之后,我们就可以说,呃,只过它这一个定点。因为如果还有其他定点的话,两个定点,比如说这里是 k, 那 我这个 m n 的 这个圆心,这个以它为中心的圆的圆心,是不是已经过 t k 的 中垂线?那显然这是不可能的, 对吧?所以说你证明了上顶点是可以的之后,我们还可以说明他的唯一性,所以也可以这样来做,都是可以的。这个也比较简单,我们前面都讲过类似的东西。第二问, 当直线 m n 斜率存在的时候,它的外接圆和内切圆的半径分别为这个 ok, 这是直角,然后我们的这个外接圆 r 是 不是等于二分之一 m n, 对 吧? 主要是看我们这个内切圆 r 怎么来表示内切圆 r。 当我们顶角是一个直角的时候,这个 r 其实有一个比较特殊的公式,这个在很多题里面都会用到,在今年以及去年已经反复出现了,包括呃,二零二五届八十中学实验卷九 也是考这个东西,就是顶角是一个直角,我们怎么来表示内切圆半径?我们来看,这是我们的一条角缝线,于是这里是 a, 我 们来写这个 这个东西,这里是垂直的吗?这是 r, 这是 r, 所以 加上顶角是垂直的。其实我们什么,其实我们这边不妨设为 a, 这个 a 和 r 是 不是相等的?因为这个是一个正方形嘛,对吧?我们首先这里都是直角,所以它是个矩形,它这个矩形我们 r 跟 r 又相等,所以它是不是一个正方形?它这个正方形的话,我们 r 是 不是等于 a? 那我们在讲到内切圆的时候,经常说,我们经常按照切点来给它分成三个长度来算,那我们就来看这边是不是 b, 这边是不是 b 和 c, 我 们这里再做一个垂线 坐在这里吧,那这张就是 c, 这张是 b 嘛?所以有一个角是直角的内切圆半径,我们经常怎么表示它就等于我们的二分之一。这个, 呃,我们是 t, 或者这个叫 a 吧,因为这里刚用的是 t, 但实际上它上的链应该是 a, 我 们的 am 加上二分之一 an, 再减掉二分之一 m n, 这个非常常见啊,也是非常好用的一个代换。当你的顶角是个直角的时候, ok, 对 吧?因为我们 r 就 等于 a, 我 们 a 的 话就可以这两边相加,然后再减到这边再除以二这东西,然后我们就根据这个来套进去,我们就会有我们的 am 加上我们的 a n, 应该是等于我们根号二倍的 m n 的, 又是直角又是 a m 加 a n 等于根号二倍的 m n。 其实你套一个购物店里,或者说你直接瞪眼法,你都能瞪出来,我们 a m 是 不是应该等于 a n, 对吧?当然你也可以写个购物定里,然后把我们这个带进去,也同样可以得到我们这个结论, ok, 我 们到这个结论之后呢?我们下一步是不是简单了,也就说我们现在有一个顶点 a, 有 一条直线是过这个 q 点的,对吧?啊?这个 e 点的,不好意思 或者一点的,然后它是一个等腰直角三角形,然后求 m n 的 斜率。那首先是不是我横着这根一定是可以的,对吧?那我们就看其他的行不行,其他的行不行的话,你只需要设一个 k, 然后我们进行计算就可以了。那这个过程是比较简单的, 我们只需要把这个 k 设出来。设出来之后呢,我们看怎么表示,那是不是我们取它的中点, 对吧?那我们这里是垂直的,你就可以把它解出来了吗?这就比较简单了,对吧?那我们最后解出来呢? k 等于零, 或者 k 等于正负五分之杠五。那这个解的过程就不再去多说了,就是一个比较轻松的一个计算的过程。 ok, 这是我们的十九题。
 01:30查看AI文稿AI文稿
01:30查看AI文稿AI文稿合肥市一模考试马上就要开始了,就在二月九号十号正式进行,前两天,合肥市教科院召开了一模考试的相关启动会议,这里呢,我也跟大家简单的汇报一下本次考试的一些整体情况。先说报名数据啊,本次考试合肥市加上四线一市总报名人数达到了七万三千二百二十六人,涉及了一百零六所高中学校,整体体量还是相当可观的。 全市共设置了两千两百个考场,其中合肥市区三十九所高中总共有两万五千六百一十五名考生参加, 选择历史方向的学生一共有七千一百九十五人,物理方向报考人数为一万八千四百二十人,四线一式合计参考人数为四万两千两百零九人。 具体来看,巢湖市十三所高中共有五千九百六十九名考生,肥东县十八所高中报名人数一万两千六百二十六人。长丰县十四所高中参加考试的人有八千六百五十二人。庐江县八所高中参考人数七千七百二十二人。 再说月价安排啊,考试结束后,将于二月十号十一号在合肥一中滨湖校区集中阅卷,到了十二号各校就可以把答题卡领回。 不过需要说明的是啊,这次考试成绩不对外公开,也不进行排名,原因很明确,一模的作用更多是用来发现问题,查漏补缺,而不是给学生下结论。对于同学和家长来说,合肥一模这么多年来的认可度一直不低,也是高三阶段迄今为止规模最大的一次统一考试。 如果你不是合肥考生或者人在外地,但属于安徽省内,合肥一模试卷还是很有参考价值的,建议一定要认真做一做。关注我在后台私信合肥一模考试结束后,我会把试卷发给大家。
 04:43查看AI文稿AI文稿
04:43查看AI文稿AI文稿同学们,安徽省顶尖名校合肥一六八中学的异模卷来了!别被他朴实的题面骗了,这套卷子没有一道题是白给的,做完它,你只会感慨基本功不扎实,大题直接压火, 思维不灵活,小题寸步难行,易整体评价。这套异模卷前六题是标准送分题,集合必要条件定义不等式判断 分段函数、单调性周期偶函数,但第二题必要不充分,条件转化。第四题不等式作差比较,已经暗示了他重视逻辑推理的基调。 从第七题奇偶性加单调性减抽象不等式开始进入中档难度区。第八题多元最值,需要整体换元加判别式锁定范围,是很多同学的第一个卡点到多选题。第十题 抽象函数性质第十一题同够零点比较,已经完全是高考压轴小题配置解答题第十七题任意存在问题第十九题地铁运营建模,则体现了用数学解决现实问题的新高考风向。二、 重点题目第八题多元最值问题考点,等式变形,整体换元倒数求最值。解析思路,从 a b 减一等于 b 变形出一大加一, b 等于一,发现 a 加 b 有 a b 可统一设为 利用方程。有十根条件, delta 大 于等于零求出 t 大 于等于四。构造函数 f t 等于二分之一 t 二减 t 减三零 l n t 求导,找最值一错点, 忽略 a、 b 大 于零的范围,导致 t 范围扩大,求导后忘记检验 t 等于四的端点值。备考重点,遇到双变量等式,先想整体换元最值问题,务必先定范围再求导。第十题抽象函数性质考点,函数方程负值,其偶性对称性推导 解析思路,观察 f x 加 y 加 f x, f y 等于二, f x f y 联想于弦和差公式,例, x 等于 y 等于零,但 f 等于,若为零,则函数恒为零,舍去 例, x 等于零,推出偶函数对 f, e 加 x 加 f, e 减 x 等于零, f 求导得导函数对称性易错点,误以为 f 零等于零,未发现 f e 加 x 加 f, e 减 x 等于零是关键桥梁。备考重点,抽象函数多元于三角函数或指数函数模型求导是研究对称性的利器。第十一题,同构双零点比较考点,反函数对称性同构变形 构造函数比大小。解题思路有,一加 x 一 等于零,有 x, 二加 l n, x 二等于零,发现 x 一 等于减乘一, l n x 二等于减乘二,利用反函数对称性得 x 二等于 x 一, 进而有 x, e 等于 l n x 二比较大小,需构造 f, x 等于 x 减 l n x。 研究单调性易错点为识别出 x e 与 x 二,通过指数对数互为反函数关系范围判断不准备考重点, 零点差问题,通法构造单调函数求值域多画图帮助理解反函数对称。第十七题,任意存在行双变量考点,逻辑条件转化参数分离同构换元解析思路,任意 x 一 存在 x, 二转化为 f, max 小 于等于颠敏 分离参数的 e 大 于等于 x, x 加 x 减 l n x 换元 t 等于 x 减 l, n, x 化为 a 大 于等于 at 加 t 求 t e 时的最小值 e 错点,逻辑条件转化错误,换元后为注意新元范围。 备考重点,任意存在题必须先翻译逻辑参数分离后优先观察能否同构换元。第十九题,函数最值应用题考点,分段函数见模加最值解析思路,见模 三小于等于 t 十十 s t 等于负三十 t 平方加四百八十十小于等于 t 小 于等于二十十 s, t 等于四百八十化解 m t 第一段两百零八减十二 t 加一百九十二 n t 第二段一零零八 t 三十二求最值。第一段用基本不等式 t 等于四十取等 m 等于一百一十二。第二段单调减 t 等于十十 m 等于六十八 eight 比较得 t 等于四分钟时收益最大为一百一十二元易错点望定义域三小于等于 t 小 于等于二十会验 t 等于四,能否去到备考重点,分段函数先建模再分段求最值。对勾形用基本不等式虚远等号应用题,答案需符合实际意义。 三、备考指引九十分档四科第一到六十二十三十五比十六题,保证基础题零失误,一百二十分档突破第七十一、十四十八题 重点训练,代数变形与逻辑转化一百四十分档,吃透第十一一一四一七题,理解题目背后的函数模型与思想方法。下期想看哪个省市的异模名校卷解析评论区告诉我,如果觉得这个视频对你有一点点帮助,记得点赞收藏,这对我很重要!
84高一高二高三试卷




