sin arcsinx等于多少
嘿,大家好,数学是思维体操,我是考研数学杰哥。反三角函数的欠套一直以来是很多学生学习的疑惑点,好多同学搞不清楚三引二克三引 x 等于多少,以及二克三引三引 x 等于多少?很多同学会误认为二克三引三引 x 呢,直接等于 x, 其实很容易知道这是错误的,因为 a x 三以三 e x 很明显是周期函数,以二派为周期,但是 x 呢,并不是周期函数,所以显然不相等。 好不容易搞懂了三引二克三引 x 等于多少,以及二克三引三引 x 等于多少?我们 cosine 二克 cosine x 以及二克 cosine cosine x 又等于多少呢?又不知道啊。然后呢,二克 tangent tangent x 以及 tangent act tangent x 又等于多少呢?直接很多同学就一脸懵逼,被我说中, 同学呢,可以在弹幕上扣个一,大家看视频学知识,多跟杰哥互动互动啊,你们都是我的弟子,虽然不会见面,但是希望我的课程对大家有用,今天我就用一节课的时间教会你直接把阿克三以三以 x, 阿克扣三以扣三 x 以及阿克 tangent x 图像给画出来, 我让你知道,不论 x 取什么,你都能够把它解出来。那我们系好安全带,安全发车上课。 好,我们一起来上课,反三角函数欠套,一个视频帮你永久解决啊!听完我这节课呢,可以直接超神 反三角二千套,是很多题目的设计的一些细节啊,由于很多颜宝呢,呃,在课程中没有专门学习过此细节,所以在做题过程中会理所当然的认为某一些错误的结论啊,所以说很多时候呢,很多同学会问, 今天呢,我希望把这个问题呢给终结掉啊,这个课呢,适合所有学习数学的考研学生,我们首先要知道以下几个常识,首先第一个, saying 二和 saying cosine 二和 cosine tender act tender 永远都等,都等于 x, 横等。 接着我们再说 ak 三以三以 x, ak cosin cosin x, ak tangen tangenex 啊,就把他俩的位置换一下,他俩位置换一下,他俩位置换一下就不等了。很容易理解, 这三个函数全部都是周期函数,而我们的 x 并不是周期函数,所以你要画等号是不可能的,对不对?这是第一个。第二个就是我们 y 等于三, x 在 x 属于负二分之派到正二分之派上的反函数是 x 等于 x, 以 y。 好,我们现在呢,我们看一下, y 等于 x, y 等于三 e, x 啊,这是咱们 y 等于三 e, x, x 属于 r, 那 y 等于三 x, x 属于 r 的过程中,它不是一个单调函数, 它不是一个单调函数,就会导致一个 y, k 对应很多个 x, 所以 y 等于 c, x, x 属于,而这个呢,它是无法函数的。 好,现在我只需要做一个改变,我让 x 呢属于负二分之派到正二分之派, 也就是说,我现在选取这么一小节,我们知道 y 等于三, x 在负二分之派到正二分之派上,它是单调的, 单调递增的,一个 x 对应一个 y, 一个 y 对应一个 x, 所以这个情况下呢,它的反函数是 x 等于 r, c, c, y 啊,这个呢,是咱们这个数学家规定的啊。好,紧接着 我们再说,如果说呢,我想要知道,我想要知道, y 等于三 x, x 属于二分之派到二分之三派上的 反函数,怎么去求呢?你看,我们这一段也是单调的呀,所以它理音是存在反函数的,怎么去求?各位注意,我们呢,可以通过 x 等于 a x n y 去求,我现在画一条线,这就是 y 等于 y。 好,各位注意,当有了 y 之后,这个 x 呢,横坐标就是 a x n 以 y, 对吧?好,那我们来看这一点啊,这一点的横坐标,它实际上就是派减 ac 三引派, 为什么呢?因为这两点呢?关于直线 x 等于二分之派对称,所以它们的坐标之和除以二,应该是等于二分之派的。你看,派减 x 三于 y, 加上 x 三于 y 除以二,正好是我们的二分之派。 好,那也就是说它的反函数实际上是谁?是 x 等于派减 act 散以外, 对吧?当然,我们的 y 呢,全都是属于负一到一的,这个毋庸置疑。所以你会发现我们三 e x 呢,它在不同的 单调区间内,它的反函数呢,长相是不一样的。好,那比如说我们这一段,我再画一段这一段, 哎,这一段的是三 x 呢?在二分之三派到二分之五派啊,比如说 y 等于 三 e x, 当 x 属于二分之三派到二分之五派的时候,它的反应是什么呢?它实际上是二派加一个 r c c y。 有同学说,为什么呢?你看这个点和这个点,相当于 他挪了一个二派到这了,对不对?好,我只要知道这一点,坐标是 x 三以外呢?我加个二派,就知道这一点的坐标,横坐横坐标就是 xa, 二派加一个 x 以外, 对吧?好的,那么我们先把这个第二个给记住啊,这个是比较重要的。好,接着我们看第三个, y 等于 cosin x, x 属于零道派的反函数,是 x 等于 act cosin y。 那我们来看一下 cosin x 图像, 我们 cos x 图像呢?长这个样子。那么接着我们刚才所讲的 y 点 r 和 cos x 呢? y 等于 q 三 x 啊, x 属于 r, 它是无法函数的。我如果说想要去 求反函数,必须要指定某个单调区间,那好说,现在我就指定一个领导派,哎,指定一个领导派,那当 x 属于领导派的时候, 数学家规定它的反函数是 x 等于 a cross x, 呃, crossing y 啊,好,那当然, y 是属于我们负一到一啊。好,那同学们,现在呢?我把这个领导派给他摆改成了派的二派, 我想再去求我们 y 等于 q 三 x 的反函数。那好说,现在呢,我们实际上说的是这一段了, 就是二排, pad 二排啊,这一段的反向数是多少?各位来看,我画一条线, 这是 y 等于 y。 好,当 y 已知时,这一点的横坐标呢?实际上就是 arc 啊, cosine y 啊。好,那请问我现在这一点啊, 这一点它的横坐标是多少呢?运用咱们刚才对称的理论, 这一点坐标应该是二派,减去 a, q, c y。 很显然嘛,这个点和这个点关于直线 x 等于派对称,所以它俩相加除以二,应该是等于我们的 pa 的,所以很显然,这个时候反而说是 x 等于二派,减去 a, c, q, c y, 对吧?哎,依次类推,我只要知道 y 点, cosex 在零道派上的,反而说是它,那我可以求出来, y 等于 cos x 任意的单调区间上的方函数。好,那紧接着呢,我们 y 等于 tangent x, 我们 tangent x 呢,它周期是 pa, 对呗,啊,它还有一个间接线,它方函数是 x x x 等于 act tangent y。 那么如果说我们想要去求 x 属于二分之派到二分之三派上的反函数的话,怎么去求呢?我还是画一条线 换颜色之后呢?我们知道啊,这是 y 等于 y, 那么已知这一点呢?坐标是 uptangeny, 那么他俩呢?周期相当于他加个派啊,所以这边应该是派加一个阿克 tangine y, 所以 y 等于 tangine x x x 属于二分之派到二分之三派时,这时候反而说是派 x 等于派加阿克 tangine 的 y, 对吧?好,所以这几点常识呢?首先得知道好,知道这个常识之后呢,我们现在把二科三以三 e x 图像给画出来啊,通过这个图像呢,以后同学们呢,就可以直接把二科三以三 e x 呢,到底等于多少直接写出来啊。 那这时候你看啊,首先 y 等于 arc 三 n 三 e x, 它的周期是多少? 周期为二派,因为三引的周期是二派,对吧?好,呃,我们现在规定一下啊,叫什么呢? 当 x 属于负二分之派到正二分之派的时候,当 x 属于负二分之派到正二分之派的时候,我们 y 等于三 e x, 它的反函数 是谁呢?是 x 等于 arc 三以 y 嘛,这是咱们刚才的常识。那现在呢,我们在这儿,由于 y 等于三 x, 反正说是他,所以我可以直接我 a x c 引我把 y 呢等于三 x 往里带, 哎,你就会发现, x n e x 呢,这时候就等于 x, 哎,就等于 x, 好,那么就是 x, x 属于负二分之排到正二分之排,这是很显然的嘛,对不对?好的, 当 x 属于二分之派到二分之三派的时候,我们 y 等于三 e x, 它的反函数 此时是多少呢?哎,我们已经说过了,我们二分之派到二分之三派是这条线,对不对?好, 我现在呢,这是 y 等于 y 这一点,这一点的横坐标是 a x saying y, 对不对?好,那 我们这一点的横坐标应该是一个派减 a c c y, 好,所以我们 y 零三 x 在二分之派到二分之三派上,反函数是派减 up 三以外,对吧?好,此时 我把我们的 y 等于三 x, 因为这时候 y 还是等于三 x 嘛,我往里带有派减去 ac 三引三引 x, 那么就说 x 是等于派减二克三引三引 x, 所以我们推出来 ac 三引 三 e x 呢,实际上是等于一个派减 x, 所以这些时候是一个派减 x。 i x 属于二分之派到二分之三派。好,那你看,从负二分之派到二分之三派,正好一个二派周期, 所以这个情况下呢,我们可以来画个图。好,这是我们负二分之派,这是我们正二分之派,这是我们的派,这是我们的二分之三派。很显然,负二分之派到正二分之派呢,是 x 啊, 好,那 x 斜率为一。好,那我们二分之 pad 到二分之三 pad 呢?是派减 x, 那么零点呢,是 pad 斜率为一,对, 对不对?好,那一个周期已经画完了。这种王二派,那在其他方面的都都都长这个样子了,对不对啊?就一直是这种直线。那很显然,你看这个呢,是方程,是 y d x 啊, 这个方程呢,是 y 等于派减 x, 那请问这个方程是什么呢?当然我们很明白的知道他的斜率是一,肯定是 x, 然后呢,加一个 b, 对吧?加一个 b, 由于呢,它的零点是多少?零点是二派,零点是二派,所以当 x 等于二派的时候呢, 它是零啊,所以零等于二派,加一个 b, 显然 b 呢,是负二派好,所以这个方程是 x 减二派,也就意味着是 什么呢?当我们 x 属于二分之三派到二分之五派的时候,我们这里应该是写上 x 减二派, 当 x 这个范围的时候, x 三与三 x 仍然是等于它。好,那我们这个图画出来了,是不是一切都一目了然了?那这个呢,是不是好像斜率也是负一嘛?负 x 加一个 b, 由于呢,它的零点是多少? 零派,二派?三派,那这就是我们的一个负 x 加三派啊,三派减 x, 所以很容易能够搞定。那我们 ark 三三 x 图像帮助大家画完了啊,那我们来看一下 ark q 三 q 三 x 图像,实际上它也是周期函数,它长的样子呢,也是这种折线形式的。很显然, x 属于零道派的时候呢, y 等于 q 三 x 与 x 等于 r x q 三 y 呢, 是互为反函数的。那这种情况下呢,我们把 y 等于 cos x 往这里可以带啊,那就是 arc cosin cosin x 了,那你看它等于它, 那这个情况下呢, a 和 cosin cosin x 是和 x 相等的啊, 当 x 属于零到派的时候,那么当 x 属于我们派到二派的时候呢? 我们 y 等于 cosine x, 它与 x 等于二派减二 x cosine y 互为法函数啊,那这刚才已经已经解释过了,对不对? 好,这是零道派,这是派的二派,画一个 y 等于 y 啊,这一点呢,由于我们知道 是 a x cosine y 啊,这个是 x 等于派,所以我知道这一点的横坐标就是二派减去 a x cosine y 啊,因为这两者关于直线 x 等于派对称,所以它们的 横坐标相加除以二,应该是等于我们的派啊,那这个情况呢,我们可以把 y 等于 q 三 x 再往这里带啊,有二派减, 减去 a c 扣三,这边是扣三 x, 好,所以 a c 扣三扣三 x 这时候等于多少呢?把它往这挪,把它往那挪啊,那就是一个二派减 x 了。好,那这是二派减 x 啊, x 属于一个 零道派。呃,二派的二派,我们知道二个 cosin cosin x 也是周期为二派的啊,所以我现在呢,把一个周期先画出来。零到派上, 这是二分之派,这是派,这是二分,这是二分之三派,这是二派。零到派上是 x, 那就长这个样子,零到派上好,派到二派上,二派减 x, 这是 一个周期,好,那么在其他地方呢,也是这样画,对不对?很好看了啊,这个呢,是 y 等 x, 这个呢是 y 等二派减 x, 这个呢?哎,由于它的 斜率呢,也是我们的一,有 x 加一个 b, 零点呢,是二派,那让他减二派,对吧?好,所以我们可以把所有的这个图像都给画出来,而且这个方程也容易求,什么二可扣三扣三, x 也画出来了。 好,紧接着我们看 arc tangentinex 图像,那你看, 我们知道,当 x 属于负二分之派到正二分之派的时候, y 是等于摊进的, x 与 x 等于 arc tangent y 互为互为反函数,这个时候把 y 等于 tangent x, 可以往这里带,那就是 arc tangent tangent x。 好,那这时候呢? x 等于它。好,所以 x tangen tangen x 等于。当 x 属于负二分之派到正二分之派的时候,它就是 x。 注意到我们 time in x 周期是派,而负二分之派到正二分派正好是一个周期。哎,所以这个图呢,就画完了啊。那各位来看,负二分派到正二分之派是 x 啊,是 x, 那么所以它的周期就一直长这个样子,哎,它就一直长这个样子 好,比如说 x 呢,属于二分之派到二分之三派,那这个方程等于多少呢?啊?它斜率是一, 我的 x 加 b 零点呢,哎,这是零,这是我们的派好,那就是减派,就是 x 减一个派,所以 a x tint x, 当 x 在这个范围内时候,它是等于 x 减派的,对吧?好,所以这个图像呢,也帮助大家画出来了,全是周期函数。 好,那我们再看 y 等于 a q c 三 x 图像,各位来看啊,这个里面呢,有一个比较重要的等式,叫什么呢?叫 a c q 三 u 加 a c 三 u 等于二分之派,这个是横等式,以及 a 克 type g 的 u 加 r c 靠 t t 的 u 也是很等式,也都等于二分之牌。所以我们想要画出它的图像,那我们要知道, y 等于 r 克 call saying c x 实际上可以写成, 我把把这个里面的 u 呢,看作是三 x 的话,它就可以写成二分之派,减去 a c 三 三引 x, 对不对?而 arc 三引三引 x 图像呢?我们刚才是不是已经已经画出来了,哎,是长这个样子对不对?好,填一个符号, 填一个符号,在网上整体挪一个二分之派,对不对?咱们就出来了,所以说很好弄啊,我们这个时候呢,谁要是随便可以写一下,当 x 是属于负二分之派到正二分之派的时候,那这个呢?是 x, 所以它是二分之派减 x, 那当 x 属于二分之派到二分之三派的时候, 那这个呢?实际上是它等于派减 x 啊,那二分之派减去派减 x, 那现在就是 x 减去一个二分之派啊,是不是很容易能写出来啊?所以 accord cosine 呢,也是一个很简单的这种周期函数的形式, 周期是个二派,我们把二分之派减 x 画出来, 这是二分之派。另外呢, x 减二分之派是这样的,哎,他是长这个样子的,这是负二分之派,这是二, 二分之三排好,周期二排好。所以这个图呢,是我们 arc causing 三 x 图,实际上如果让你去再去画我们 arc saying cosine x 图,也就是说想要去求它等于多少也是一样的。我把它写成二分之 pad 减去 arc cosine cosine x 嘛,利用它的特性来把它计算出来。 好,那如果说我让你计算 arc tangent cold tangent x, 怎么算呢?哎,我让你写成二分之 pad 减去 act tanging act cold tangent cold tangent x, 对不对啊?或者说这边呢? arc call tangent tangent x, 哎,我让你写成 arc tangent tangent x, 总之,你知道这个就可以把它算出来,所以呢,混搭也是可以的啊。 那我讲到这里呢啊,应该是属于说是讲的比较清楚了,同学们呢要下课把,这几个呢要总结总结,真的,当你总结过后,你会发现 三角反三角,他们互相欠套,对你来说是易如反掌,就跟翻个手掌那么简单好不好, 听懂同学可以在弹幕扣个六六六啊。扣个六六六。好,那咱们今天课程到这里啊,如果视频对大家有帮助的话啊,希望大家能给杰哥三连,多多支持杰哥创作好不好,那咱们今天课程到这里,我们下节课再见。拜拜。
粉丝2.4万获赞21.7万
相关视频
 04:33查看AI文稿AI文稿
04:33查看AI文稿AI文稿哈喽,大家好,数学式思维体操,我是考研数学杰哥,关注杰哥学习更多的考研数学技巧,养成先在后干的好习惯。那今天呢,我们的课程主题呢,就是我们 accent 三 e x 和三 a ac 三 e x 到底等于多少?杰哥呢,可以在几分钟之内让你快速学会并且记住啊。首先我们要 看最简单的三引 a c 三引 x, 这个呢,我们就把它记成,它就是等于 x, 只要 x 属于负一到一都成立。但另外一方面呢,我们 y 等于 a c 三引 x 呢,它的定义域 就是 x 属于负一到一。好,所以只要这个 x 呢能够带到咱们 accent x 里面,那么三引 accent x 就等于 x, 所以一般我把它看作是一个横成立的。那第二个就是我们 a x 三引三引 x, 它等于 x, 有一个条件,就是 x 属于我们的负二分之派到正二分之派。 那不同于上面我们三 e x, 它的定义域呢,是一个 r, 那也就是说在这个定义域内,只有 x 满足从负二分之派到正二分之派这一小段的情况下,我们 a x in 三 e x 才等于我们的 x, 那如果 x 属于其他区,怎么去计算呢?比如说当 x 属于我们二分之派到二分之三派时,我们 up saying 三 e x 怎么去计算?那这时候呢,我们就以它为基准啊,以这个为基准咱们去计算啊。同志们,我们这时候就利用咱们的诱导工 是我们 seine x 和 seine 派减 x, 这是咱的诱导公式吗? seine 啊法等于 seine 派减啊法。那么现在只要 x 属于二分之派到二分之三派, 那么负 x 呢?就属于负二分之三派到我们的负二分之派,那么派减 x 呢?是不是就属于我们的这个负二分之派到我们的二分之派啊?好,那么根据咱的诱导公式,三引 x, 我给它写成三引一个派减 x。 好,那你看这么一坨呢,我给它当成是一个 u 啊,我给它当成是一个 u, 那这个 u 是属于啥? u 是属于负二分之派到正二分之派的,根据我们这个第二啊,根据我们这个第二, 只要 x 属于负二分之派到正二分之派,那么二克三引三引 x 就等于 x, 那也就是说他应该等于我们这个 u 啊,实际上就是等于我们的派减 x。 哎,那么我们是不是就通过咱们的诱导公式把它给写出来了啊?他就是我们的一个派减 x。 那你想,如果说我们这个 x 呢, 熟于二分之三派到二分之五派,我现在又让你去计算 upsein 三 e x 等于多少,你看我将这个区间呢?我让他向左平移二派个单位,他是不是就变到负二分之派到咱们的正二分之派了? 那好,那么我们还是一样根据我们三音呢,它是个周期函数啊,我们 x 减掉一个二排, 三引 x 减二派和三引 x 呢,是相等的,而且这个时候我们 x 减二派,把它当做是一个 u 的话 啊,把它当做这个 u 的话,那这个 u 呢,就属于我们这个负二分之派到正二分之派,又根据我们的二呢,可以把它写成我们的 u, 就等于我们的 u u, 是,这时候就是我们 x 减去我们的一个二派, 对吧?好,那这个呢,就是我们在二呃,在决定我们二个三引三引 x 等于多少和三引二个三引 x 等于多少的一个小技巧啊。那再总结一下, 三引二克三引 x 等于 x 一般都是横成立的,只要保证我们二克三引 x 呢有意义。第二个就是当 x 属于负二分之派到正二分之派的时候,记住这个公式,然后当 x 不属于我们负二分之派到正二分之派时,我们就使用咱的诱导公式, 将我们这个 x 呢从其他区间呢拉到我们的这个负二分之派到正二分之派之间。今天这个知识点讲完了,那如果视频对你有帮助的话,希望大家能够给杰哥多多点赞,投币转发收藏,多多支持杰哥的创作,那我们下期节目再见了,拜拜。
1808考研数学杰哥(线下)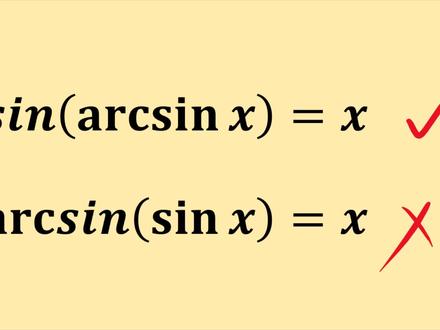 03:01查看AI文稿AI文稿
03:01查看AI文稿AI文稿最近看到一个十分特别的知识点啊,三 x 的反人数外面再套一个三等于 x 是对的,但是三 x 外面套一个反人数啊,等于 x 却是错的啊,大家可以思考一下,为什么会这样啊? 好,我们看啊,首先啊,我们去看一下三 x 本身的一个函数图像,然后再去了解一下他的反函数的图像, y 等于三 x 的图像有个特点啊,一个外字可以对应好多 x, 但是一个 x 只能对应一个外字啊, 也就是说有一个 x 的话,肯定能够产生一个唯一的 y, 这就是函数的一个特点,那么他的反数图像该怎么画呢? 凡数不就是把 xy 互换吗?大家开始画的时候肯定会画成这个样子啊,但是这个肯定是错的啊,如果这个是 y 等于 x 三 x, 那么他的一个 x 可以对应好多外啊,这跟函数的一个一应射的关系,一对应的关系是违背的啊,那如何让他产生一对应的关系呢?我们只能取一个区间啊,这个时候他的定义啊, 是负一到一,他的直域是负二分之派到二分之派,只有在这个区间里面啊,我们才能截取出一段啊, 一一对应的一个关系啊。所以啊,在这个定义直域的一个前提之下,我们才能判断 这两个是哪个式子是成立的啊,他给出了这样一个式子,那么肯定就可以判断出 x 的一个定义啊, x 属于负一到一之间,在这个前提之下啊,我们假设 y 等于, 那么这个 y 的范围啊,是负二分之派到二分之派之间,得到上外肯定对应啊,一个唯一的值啊,它的值也是对应 x 的, 所以啊,他成立啊,他是一对应的一个关系的。但是针对于这个二来说啊,却不确定呢, 因为这个是只能确定三 x 的范围是负一到一之间啊,而三 x 就飞到一之间的话, x 的值可以取变富无穷到正无穷啊。但是呢,这个的值欲啊,注定呢,这个整体的这个值 只能属于负二分之派到二分之派。也就是说啊,本来这个 x 是可以求出各种各样的值的啊, 现在他把他的纸给缩小了,所以说啊,这个不成立啊,关注我,让学习变得更有趣。
996火星课堂 07:07查看AI文稿AI文稿
07:07查看AI文稿AI文稿大家好,这期讲欧拉公式,在漫长的数学历史长河当中,诞生了无数美丽的数学公式,他们宛如一颗颗璀璨的明珠,光彩夺目,而只有他被称为上帝公式,他就是欧拉公式。那我们来看一下他有什么特别之处啊。 它的形式是这样的,一的 i x 次方等于 cosine x 加上 i 乘以三 x, 其中一是自然长数, i 是虚数沙眼, cosine 呢,是三角函数。当 x 等于派的时候啊,公式就变成了一的 ipi, 次方等于负一,这个就是欧拉横等式。 这个等式包含了自然长数、虚数、圆周率和自然数。每一个单拿出来啊,在数学史上都是非常炸裂的存在。而欧拉公式竟然以一种极其简洁的形式,轻描淡写般把他们 结合了在一起,在以简洁唯美的数学世界里啊,难怪他会被称为上帝公式吧。事实上,与欧拉公式相近的公式,在此之前就已经被发现了。其实这也不奇怪,我讲虚数的那期视频呢,也有推导到类似的结果啊, 例如一七零七年,法国数学家蒂莫福就发现了一个这样的公式, cosine x 加减 i 乘以三 x 的 n 次方,它是等于 cosine n x 加减 i 乘以三 n x 的。 又例如,一七一二年,英国数学家罗杰科特斯在研究螺旋线无常的时候呢,就得出了一个这样的公式, l n cosinex 加上 i 乘三 x 呢,它是等于 ix 的 啊,这里注意一下啊, l n 这个符号呢,是后来欧拉取的啊,是表示自然对数的意思。在此之前,数学家们呢,都是用别的方法去表示自然对数的啊,这里我为了大家好理解,直接就用 用了 l n 啊,包括虚数 i 也是后来欧拉给的符号,在此之前呢,虚数都被写作根号负一,我为了方便表达啊,也是直接用了 i 的啊。 这个公式呢,可以说是无限接近欧拉公式了,只要两边同时取一为底的指数操作就可以了。不过科特斯在一七一六年突然离世,这一结果呢,也从未正式发表过。接下来为了说明欧拉公式,我得先讲一下这个自然长数是什么啊? 自然常数一,其实我们在高中的时候呢,就接触过了,他和 pi 一样,也是一个物理数来的,他约等于二点七一八二八。 自然长数又被称为欧拉数,但是欧拉数却不是欧拉发现的,是雅阁部博努力在研究存款复利的时候发现的。注意一下这里的博努力和流体力学的博努力啊,不是一个人, 流体力学的是丹尼尔博努力啊,他是雅格布的侄子。这里说明一啊,其实是有两个数学模型可以选的,一个呢,是一年之内无穷次存取 gc 啊,博努力用的就是这个。第二个呢,就是定期只存取一次啊,但是你可以存无穷多年, 不过不同年份的定期啊,就会对应到不同的利率,因为时间无穷细分这个事情对我来说呢,有点离谱啊,所以我这里用的就是第二个模型。 假如银行规定了一个这样的规则,存一年利率就是百分之一百,存两年利率就变成了百分之五十,也就是二分之一,存三年利率变为三分之一,而存 n 年呢,利率就变成 n 分之一, 复利的意思就是今年的本加息呢,会变成下一年的本啊。好,那么我们用一个具体的例子来说明啊,我有一块钱, 存一年之后,到手就是一加上一乘以百分百等于二。存两年,最后到手呢,就是一加上二分之一,加上一加上二分一,再乘以二分之一的,也就是一加二分一的二次方,等于二点二五。 存三年,最后到手的就是一加上三分之一的三次方,等于二点三七的,以此类推啊。存 n 年,最后呢,到手就是一加上 n 分之一的 n 次方。哎,这个时候好像发现存的越久,赚的就越多。如果我存无穷多年,那么本息会不会最后就是无穷多呢? 不会,他只会无限趋向于二点七一八二八点点点点,对吧?甚至呢都到不了二点七二。我们可以画一个一加上 x 分之一的 x 次方的函数图像啊,可以明显看到,函数值到了二点七一左右啊, 就上不去了。欧拉在他后来的注册中多次引用到了这个数,并且给了他一个符号一,所以这个数也被后人叫做欧拉数了。这个自然长数有什么特别的地方呢啊,我们来看一下啊,假如有一个指数函数是以一为底的,也就是 y 等于一的 x 次方, 我们随便找一个点吧,例如 x 等于二,那它的函数值呢,就是一的平方,在这一个点的倒数,也就是切线的斜率,它也是一的平方。 函数曲线与 x 轴围成的面积呢,它也还是一的平方。放眼整个数学界,这个函数的特性啊,也是独一份的啊, 当然,三角函数三 x 啊,求两次导之后呢,会变成自己的相反数啊,这个特性倒是和 e 的 x 方啊有点类似,感觉这两个函数冥冥之中就是有关联的。当然,对复数领域和三角函数领域研究颇深的 欧拉也是这样认为的。一七四八年,欧拉发表了一篇名为无限研究导论的论文,里面就引用了蒂莫夫的公式啊, 我们来看一下啊,两式相加除以二,就得到了 cosine 的 n x。 两式相减除以二 i 就得到了 cyan 的 n x。 欧拉大胆的把 x 取了无穷小,于是呢,就有了三眼 x 是等价于 x 的,扣上 x 呢,是等价于一的啊,那么式子呢,就变成了这样, 然后再取 n 为无穷大,令到 n x 等于 k 啊,那么就有 x 呢,是等于 k 除以 n 的。最终的式子呢,又变成了这样。 哎,大家看,这不就是我们刚刚讲过复利的计算形式吗?这个其实就是一的 i k 次方,而这个呢,就是一的负 i k 次方, 所以最后 q 三 k 和三 k 呢,就变成了这样。哎,我们看这两个式子,拿二式乘以 i 再加上一式, 于是乎,我们就得到了欧拉公式的最终形式码, q 三 k 加 i 三 k。 之前讲虚数的时候就提到过,它可以在副屏面上表示旋转,所以呢, e 的 i k 四方也是一样的。 举个例子,五乘以一的 i 三分之拍次方,这个数表示了负平面上五为半径,逆时针旋转了六十度所在的位置。 又例如一个负数一加 i 化成负指数,形式是怎样的呢?在负平面上画出来一加 i 的点在这,它的半径就是根号二全过的角度刚刚好是四十五度,也就是四分之派。用三角函数表示呢,就是根号二乘以 扣上四分派,加上 i 乘以三四分派,也就是根号二乘以一的 i, 四分之派次方。好。至此,欧拉公式就跟三角函数和旋转关联了到一起。 你想想啊,复离液激素还得用沙哑和抠上两种函数做基底去分解,如果用一的 ic 塔次方去做基底的话呢,一个就够了。好了,这期讲到这,下期我们讲复离液变换在复数域的展开,我们下期见。
1574有趣的理工男 00:56查看AI文稿AI文稿
00:56查看AI文稿AI文稿看到这道题的第一眼,如果你的答案等于一,那么你就掉坑了。这是一道二零二二年专升门考试数学真题天空题的第一题,当年很多同学都写的一,我们来看这道题考察的并不是第一重要极限, 那么第一重要极限这里是趋向于零的,所以我们需要对这道题进行变形,我们可以把它变成 n 分之一,呈上算以 n 的形式,那么当 n 趋向于无穷的时候,大家来判断一下 n 分之一趋向于几 分?母无穷大,那么整个分式是不是趋向于零的,对吧?所以说前面是零。好,那么当恩需让于无穷的时候,算也无穷,它是不是在正负一之间来回拨动,所以说它是一个有界变量, 零是一个无穷小量,无穷小量乘以有界变量,最终答案是不是还是无穷小量?所以说这道题等于零,你做对了吗?
3359熊哥教数学 00:38查看AI文稿AI文稿
00:38查看AI文稿AI文稿手指法,秒记三角函数,让你一辈子都忘不掉。三十,三十度往下数一根手指写一,三十,四十五度往下数两根手指写二, 三元六十度往下数一,二,三,三根手指写三口。三元三十度往上数三根手指。 火山四十五度往上数两根手指 扣三,六十度往上数一根手指, 是不是非常简单?
33.3万数学思维茹老师 02:09查看AI文稿AI文稿
02:09查看AI文稿AI文稿大家好,我是罗老师, r q 三应根号 x 的导数怎么算? r q 三应根号 x 的导数球法如下, r call 三引,根号 x 的导数等于根号下一减 x 分之一乘根号 x 的导数等于根号下一减 x 乘二倍,根号 x 再分之一等于二倍,根号下 x 减 x 平方分之一。 好,我们来讲解一下这道题。那咱们授 y 等于 r, c, c, n, 根号 x, 那这就是一个符合函数,所以我们要用换元法来求到。另, u 等于 n 号 x, 那么 y 呢,就等于了 r c, c, n 啊 u, 然后啊,咱们的 u 岛也就等于了根号 x 的导数,根号 x 也就是 x 的二分之一,所以他求导之后就为 二分之一啊,再乘以根号 x 四分之一,所以他俩合起来呢,其实就是二倍根号 x 分之一。 好歪倒,也就是二颗三一啊右的倒数呢,他就等于了 根号下一减六的平方再分之一。那因为又等于根号 x, 根号 x 平方呢,他刚好就等于了 x, 所以这里就为根号下一减 x 再分之一。 所以最终儿科三引啊,根号 x 这个函数,他的导数 就等于根号下一减 x 再分之一,乘以二倍,根号 x 分之一。乘在一起,咱们就得到了二倍根号下 x 减 x 平方再分之一。 那这个呢,就是儿科三引根号 x 导数的一个推导过程,有看懂吗?我是罗老师,关注我,咱们下期再见。
71罗姐数学 02:05查看AI文稿AI文稿
02:05查看AI文稿AI文稿哈喽,大家好,我是爽哥,那么今天给大家分享的是三角含粪指人,他的求职方法, 很多的孩子啊,从高一到高三学完之后三角还不直,还是记不住,那么今天呢,爽哥教给大家一种方法,让你快速的记住 siri 的他们从零度到九十度,所有的三十。 首先咱们来看一下适应二,那么适应零度是等于零,适应三十度等于二分之一,适应四十五度等于二分杠二,适应六十度是二分零,杠三适应九十度是一,那么这个一我在这里把它写成二分之二十,同学们看清楚啊, c 三十等于二分之一,接下来一次让他递增就可以了。那么因为 c 二法和 ctrl 法他们是不一的,所以他们的三角函数值正好是倒过来写 扣信,零度就等于一,扣信三十就等于二分之二,三四十五度,二分之二六十度,二分之一,九十度就等于零。那么同样摊位呢,他也有对应的方法看, 因为他记得三十五是三分之二三,那么他记得四十五度是一。这里啊,他们之间的关系就是三分之根号三,再乘以根号三,那么就等于一, 相当于每一项都乘以钢化三就可以了。三分之二三等于一,一乘以钢化三,就只看见了六十度 他的值,而他这个九十度是没有值的。同学们,这个是跟他的函数图像性有关系,因为咱们摊这个函数图像,他呢永远是趋于二分派,而不等于二分派,所以在 k 派加二分派这一点处是没有函数值的。那么这种方法教给大家之后,你学会了吗?
51爽哥说 03:07查看AI文稿AI文稿
03:07查看AI文稿AI文稿三十八度等于多少呢?那么一部分同学看到这个度数可能会束手无策,哎,有一部分同学他知道黄金三角形哎,这顶角为三十六度,顶角为七 十二度的,这样的一个等腰三角形,哎,他会把三十八度和这个三角形联系起来啊,为什么?因为你看一下这个三角形顶角是一个三十六度,一旦我知道 abc, 你这个三角形的三边支笔就 就可以去求三十八度了,对吧?所以呢,我们现在就去解一下这个黄金三角形,看他的三边比是多少。那这里呢,我们可以射腰是一个一底, 底边和他满足一定的比例关系,所以呢,我们设底边为 x, 然后接下来看一下七十二度,是三十六度的二倍,所以我们可以去把底角平分啊,做底角 角平分线,此时就会出现两个三十六度,那么这个度数呢,是一个一百零八度,这边呢是一个七十二度。 好,现在来看一下 a、 b、 d、 b、 c、 d 都是等腰三角形,所以这里的 b、 c 和 b、 d 以及 a、 d 都是相等的啊,都是 x x, 那么我们就可以推出来 cd 就是一个一减 x。 好,你看,设一个未知数,就可以把这个黄金三角形里面所有的线段长都给他的 x 表示出来了。接下来再做一件事情,我们发现 abc 和这里的 bcd 应该是相似的啊,跟 去 abc 啊,和这里的 bcd 相似,利用对应编程比例,一比 x 等于一个 x 比上一个一减 x, 那我们解出来 x 等于一个二分之负,一加减跟号五,显然这里的负的就给他折掉了啊。因为 x 表示的是什么 线段的长,所以呢,我们解出来 x 等于一个二分之根号五减一,哎,你会发现这个二分之根号五减一,就是我们所记得那个黄金分割笔的笔值啊,其实他也是黄金三角形这个名字的一个由来,所以啊,现在呢,我们就得到了这个黄金三角形 a bc, 他的三边比一比一,比二分之根号五减一。好,接下来要求三十八度,最直接的一个做法就是,哎,我去评分你的顶角 去求就行。那么这里老师在告诉大家另外一个做法,我可以延长 b a 到点 e, 使得 ae 等于这个 ac 都等于一个一,接下来把 ec 给他连起来,那你看一下这个角是不是就十八度啊?这里也是一个十八度,这边原来是一个七十二度,所以, 所以呢,可以得到这里的 bce 是一个直角啊,那我们就可以把这个十八度呢放在 bce 这个直角三角形里面了,所以 用他的对边 bc 比上一个斜边 b e, 也就是二分之根号五减一,比上一个一加一啊,比上一个二,所以最后的结果就是四分之根号五减一。
2641叮当-ding初中数学 04:08查看AI文稿AI文稿
04:08查看AI文稿AI文稿这是一个非常简单而且易错的方程,考场三 x 等于三,考场 x, 要解决方程啊,大家可以暂停挑战一下,我们看大部分同学是如何错的啊, 把这个看成阿法,这个看成贝塔,他们俩相同,那么阿法加贝塔肯定等于二分之派,也就是三 x 加 con, 三 x 等于二分之派, 这个可以写成根号二乘以口号三四分之派。三 x 加上三四分之派乘以口号三 x 等于二分之派,也就是根号二乘以三 x 加上四分之派等于二分之派。 而这个的范围就是负根号二到根号之间,因为这个是负一到一之间啊。 而二分之派大于公号二,因为派是三点一四嘛,一五九除以二,这个是大于一点五的啊,而一点五肯定大于公号二,所以说超过子欲了,五减五十速减, 那他到底错哪了呢?大家可以暂停调整一下,能不能找到他到底错哪了, 错在了第一步啊,他可能加个二 k 派,因为二 k 派并不影响他们相等啊。还有另外一个非常重要的原因啊, 他们不只是货鱼才能够相等,我们可以画一下,我们假设这个是阿法,这个是贝塔, 如果贝塔有一个结 在这里,那么肯定有一个贝塔一,可以跟他取一样的字啊,三贝塔等于上贝塔一。 所以说还有另外一种情况需要讨论啊,这个时候贝塔加贝塔一等于派,因为他们关于二分的派对称嘛,这个派是二分的派乘以二。 ok, 理解了,这个实际上还要讨论另外一种情况啊,第一种情况,三 x 加上考场 x 等于二分之派加二 k 派,也就是更换二倍的三 x 加上四分之派等于 二分的派加上二 k 派啊。假设他是 m, m 的范围肯定是负公号二到公号二,而这个二分的派 加二 k 派。在 k 大于或等于零时,二分之派加二 k 派 是大于一点五的,就不在子欲范围之内。当 k 小于或等于负一时,因为 k 是整数嘛,可以这样取啊,二分之派加上二 k 派要小于或等于负二分之三派肯定小于负跟二 也不在子欲范围之内啊,所以无解。同样的啊,三 x 加上一个中间亮盘阿法等于二分之派和另外一个 考三 x 加上这个啊法是等于拍的,就能够满足考三三 x 等于三考三 x 啊。 别忘了加个二 k 派,上下相减得到三 x 减空三 x 等于负二人派加上二 k 派, 也就是更换二倍的十二 x 减四分之派等于负二分之派加二可以派,同样可以证明这个无解啊, 因为这个超出了他的直域负公号二和公号之间。 ok, 更多的有趣的趣问题,可以翻看我的合集和订阅我的赞赞,关注,晚上学习变得更有趣!
1223火星课堂 03:27查看AI文稿AI文稿
03:27查看AI文稿AI文稿好了,说回咱之前那个问题啊, limit 狗区域零, sunny 狗比成狗等于一,它是对的还是不对呢?其实它是对的,因为什么呢?你平时见到的是什么?你平时见到的是 limit s 区域零, sunnys 比上 s 等于一, 现在你把这里的 s 全换成狗,他自然不也是对子吗?并且这里头已经告诉你了,这个狗是区域零,但不等于零的啊。 但是你平时常见的不是他啊,你常见的是类美,他比如说 x 区域零,这只是其中之一, x 还可以趋于其他的,比如说区域无穷,比如说区域一,比如说区域二之类的啊, 然后三人狗比成狗,并且这个狗是无穷小。好了,现在如果在 x 区零这过程中,也就是 x 不断的接近于零,但不等于零的这个极限过程中,狗也是不断的接近于零,但不等于零的,则直接写成他等于一,这是没有问题的。 比如说雷美特 x 区零散以散以 x 比上散以 x, 他等于一,这是没有问题的,因为在这个 x 不断的接近于零,但不等于零这个极限过程中,散以 x 也是不断的接近于零,但是不等于零的,所以直接写成他等于一。但是对于后面这个啊,对于后面这个例子,你来看一下 类美塔 x 区域零啊,这个极限过程就是 x 不断的靠近于零,但是不等于零了啊。看一下这个赛呀, s 乘上赛呀, s 分之一比 以上, s 乘上三呀 s 分之一,这个极限结果他就是不存在的。因为什么呢?你取这么些点,你令这些点设成一个数列, xn 等于 n 派分之一,当 s 区于零时, xn 是区于零的, 那么 n 就是在趋于无穷的,则怎么呢?则这些点是位于这个无限的被压缩的右邻域内的,这是没有问题的,并且把 xn 带到这 这个分母的函数啊,形成了什么? x n 呈上善意 sn 分之一,他就可以写成 n 派呈上善意 n 派。他是零, 你不要看他,你看他这是实实在在的零啊!零乘任何数都等于零啊,这是实实在在的零,则怎么呢? 则在这些点处会形成分母为零点,分母为零点,这个函数不存在,与函数极限定义矛盾了。定义要求的是在某空心领域内处处有定义,而你找不到, 因为他怎么的?就算你把这个空心领域无限的压缩,你总能在这个领域中找到这些点,使得什么?使得这个函数的分母为零,与函数极限定义矛盾了,则怎么的?既然与他定义矛盾了,则这个极限是不存在的。好了, 此时狗是等于 x 乘上三 s 分之一的 x 趋于零时,狗会不断的等于零,而不是趋于零,但不等于零,则怎么呢?不能说成狗趋于零,但不等于零。 如果你见到了勒美他赛运狗比成狗,你必须要看这个狗是否趋于零,但不等于零。 如果一旦像之前这个例子一样,他会不断等于零了,则这个结果应该就是不存在的了啊。对于无穷小量等价代换表扩展的时候, 我们见过这个狗区零散运狗等价与狗狗捡,散运狗等价于六分之狗立方,这个是对的,也是超级好用的,特别实用的。 因为怎么的呢?因为他已经告诉你了呀,他告诉你了什么狗去领,但狗不等于零了,所以这些都是适用的,对于表里的其他的问题,你也可以这么扩展的。
636徐子恒(考研数学) 03:45
03:45 05:11查看AI文稿AI文稿
05:11查看AI文稿AI文稿分享一个比较特别的知识啊,在一二三四五六七八九这些数字里面啊,找到一个数字,它里面藏着派,也就是说这个数字跟派的联系是最紧密的。 大家可以看一看啊,是哪个数字啊?好多人可能会选三啊,因为三点一四一五九二六吗?最开始一个是三,实际上不是的啊,是五啊, 五里面藏着这个派。好多人就疑惑了,这个五里面怎么藏着派呢?我们来看一下啊。大家可以拿出自己的计算器啊,或者打开网页啊,求三二一除以五等于多少?三二一除以五十五等于多少?三二 一除以五百五十五等于多少?我们今天去按一下啊,三一除以五等 等于零点一九八,好像跟派没有什么关系啊。再来看一个啊,等于零点零幺八,好像跟派也没有什么关系。再来试一个, ok, 零点零零幺八零跟派压根就没有关系啊,难道我要翻车呢?实际上不是的啊,是因为我们计算方法的不一样,我们采用的是一个弧度制。如果我们采用这个角度制的话,我们看啊, 第一个是零点零零三四九啊,我们写过去啊,第二个啊,等于零点零零零三幺七。 再来看第三个啊,零点零零三幺四。 ok, 我们把它写成这种形式啊,三点四九乘以十的负三,三点幺七乘以十的负四,三点一四乘以十的负。 ok, 他是不是跟三点一是越来越接近了,区别在于后面这个啊,在慢面变小哎,那我们是不是可以推出来一除以好多个五, 他是不是非常接近于三点一四一五九二六乘以十的多少次方呢? n 个五的话,他是负 n 加二。 ok, 三点一四一五九二六九二七啊。没错啊,六的后面是五啊,他近了一位啊,所以他变成 齐了。那为什么会出现这种巧合呢?这种巧合从哪里来的呢?这个就得从弧度字说起了啊,正常的啊,这样绕一圈啊,是三百六十度啊,写成弧度字是二派。我们再来看一看单位员啊。 那么这根线的长度就是十二 ct, 而这个弧长是 ct。 很明显啊,这个 c 塔比这个三 c 塔要大。但是呢,当这个 c 塔很小的时候,我们会发现啊,这个弧长和这个直线长是越来越接近的。也就是说三 s 的很小的时候,它是等于 c 塔的 前提啊。这个 c, 他用的是弧度制啊。实际上啊,这是泰勒展开的一种形式啊。 当 c 塔很小的时候, c 到五十方, c 到七十方啊,是比 c 塔更小的无穷小。所以说,他们可以忽念不计啊,只保留这个影响这个组织的 c 塔。 ok, 明白了。这个啊,我们就可以明白三一除以五,五五,好多个五,为什么 约等于派乘以十的。假设有 n 个五吧。负 n 加二。这个是怎么来的呢? 首先要知道这边的这个是度数啊,刚刚注意到啊,注意到刚刚我们的动作啊,我们刚开始算的是不相等的。最后我们换成角度制之后才能想到啊,啊, ad 是弧度制的意思。 a 点啊, d e g 啊,是 dgree 啊,角度的意思啊。 所以这个应该是角度啊。这个角度换算中,弧度是什么呢? 一除以这个乘以派除以一百八十度,这是换算乘弧度值啊。而这个跟这个有什么关系呢?非常的巧。一除以一十八是等于零点零五五。 也就是说这一段啊,可以写成一除以一十八乘以十的 n 加一次方啊。然后这一段化解就变成了三二 派除以十的 n 加二次方。我们知道这个 n 很大很大的时候啊,这个整体的数字很小,他就是派除以十的 三加二释放。这个完成了角度和弧度的一个转化。 ok, 关于这个有趣的问题,我们就分享到这里,关注我,让学习变得更有趣一点!
3089火星课堂 02:48查看AI文稿AI文稿
02:48查看AI文稿AI文稿把 a 倍的散音 x 加 b 倍的 coco x 这种形式转变成咱熟悉的正弦形函数。先提个根号 a 方加 b 方,看看,里面就变成了根号 a 方加 b 方分之 a 倍的散音 x 加根号 a 方加 b 方分之 b 倍的 coco nx。 不难看出,他俩的平方和就是一。把这个看作扩散范,那这个就是散义范。利用两角合的正线公式,他就可以写成散义 x 加范看,这不就把 a 倍的散义 x 加必备的扩散 x 变成咱熟悉的正线形函数了吗? 看来以后再遇到这种形式,你就可以直接提出根号下 a 方加 b 方进行化解。这引入了一个辅助角发,所以这个就叫做辅助角公式。注意了,这里的发一定是个具体的角,他的余弦 值就是根号下 a 方加 b 方分之 a, 他的正弦值就是根号下 a 方加 b 方分之 b。 有了这一步转化,就可以直接分析这个函数的性质了。 比如二倍的散音 x 加三倍的扩散 x, 提出一个根号下 a 方加 b 方,那就是根号十三倍的散音 x 加范。从这个式子可以直接看出,他的最大值就是根号十三,最小值就是负的根号十三。当然也可以直接看出他的周期就是二派,除以一得二派。 看来以后再遇到这种形式的三角函数,你就可以直接写出最值和周期,最值就是正负。根号下 a 方加 b 方,周期就是二,排除以 x 前面的系数。 当然在使用辅助的公式时,后面也不一定都得是 x, 都是二 x 或者都是二 x 加三分之派 照样可以做,只要他们后面跟的是完全一样的东西,你都可以用这个公式,比如三倍的散以二 x 加三分之派,加上四倍的扩散,二 x 加三分之派,因为这里都是二 x 加三分之派,所以你还是可以直接写出最大值和最小值, 最大值就是三的平方加四的平方再开方也就是五,同样的最小值就是负五。另外你也可以直接写出周期就是二派,除以二德派。 看来不管下映和扩散后面是什么,只要相同就可以用辅助角公式。以上就是辅助角公式的全部内容,一起来总结一下。 以后只要看到 a 倍的下映, x 加 b 倍的扩散 x 这种形式的函数,你就可以直接提出根号下 a 方加 b 方进行化解,它的最值就是账户根号下 a, a 方加 b 方,周期就是二排除以 x 前面的系数。注意,只要上一和扩散后面的式子相同,就可以用辅助角公式。 怎么样,明白了吗?明白的话就速速刷题去吧!
583高中数学 04:06查看AI文稿AI文稿
04:06查看AI文稿AI文稿来看今天的这道中考状元题,题面非常简单,球赛印十八度的直,但是有点为难你们了, 三十、四十五六十的正于闲置,可能你们还知道,但是十八度到底是个啥?别说初中生了,高中生都有点困难。今天咱们来通过黄金三角形这个经典模型,帮助大家解决这个问题。 对于这个三角形来说,他的顶角是三十六度,并且 ab 和 ac 相等,等腰三角形,而 而且底角七十二度,这边的 abc 也是七十二度。我们来做出角 abc 的平分线,你会发现这两个小角都是三十六度。既然三十六度三十六度,说明 ad 和 b、 bd 一定相等,那么相应的这个角度七十二度, bd 和 bc 也一定相等。 我们得到了三个等腰 abcbcd 和 adb 都是等腰三角形,我们来射出 ab 的长度 m, 射出 ad 的长度 n, 接下来我们也就能知道 cd 的长度应该是 m 减 n, 这里是 n, 这里还是 n, 接下来怎么办呢?既然知道了 bcd 的顶角三十六度, abc 的顶角也是三十六度,并且两个都是等腰三角形,那么他俩必定相似。 我们用大三角形的长边 m 比上小三角的小三角形的长边 n, 用大三角形的短边 n 比上小三角形短 短边 m 减 n, 我们得到了这样的一个分式,对于这个分式方程来说,交叉相乘,我们能得到 m 方减去 m 等于 n 方。然 然后大家一起来看,我们把他们先都挪到同一侧,挪到同一侧之后,我们得到的应该是 n 方减去 m 方加上 m, n 等于零。很多同学到这一步就被卡住了,这个方程叫什么呢?他叫做其次方程, 其是整齐的,其次是次数的次。这个内容本身应该在大学才讲,但是今天咱们把它梳理一下,大家应该也能解决问题。我需要给这个方程的两侧同时除以 m 方,得到了 m 分之恩的平方,加上 m 分之恩再减一等于零。那么这个方程你会发现 m 分之恩是不可以看成一个单独的变量了,那我就这样, m 分之恩等于 t, 也就是 t 方加上 t 再减一等于零。这个方程我们是不是会解了, t 等于什么呢? t 等于 二分之负一加减根号五,因为 t 必然是正数,所以他只能是负一加根五替的值就知道了,也就是说 n 比上 m, 我们知道了等于二分之根 五减一。如果有的同学知道的话,二分之跟五减一就叫做什么蒙娜丽莎的微笑,对不对?什么呀?零 点六一八,黄金分割数,既然他是黄金分割数了,和我们的问题有什么关系呢?我们现在过 a 点做一条垂直于 bc 的直线,你会发现这个角度就是多少度,三十六度的一半就是十八度, 那么十八度的正弦值就是 bc 的一半的长度和 ab 长度的比,也就是二分之 n 比 m, 二分之一比 m, 也就是 n 比上二 m。 孩子们把这个式子带入进去,得到的就是四分之根号五减一,黄金分割三角形,大家学会了吗?下课!
6799数学赵观察 01:14查看AI文稿AI文稿
01:14查看AI文稿AI文稿i got a question for you sure who's the president on the one dollar bill, george washington, one dollar two are you kidding me? you're the this really for me though yeah hold on i got a second question i'll go what's seventy seven plus thirty three wait a minute seventy seven and twenty three wait a hundred and tennis oh, my god dude you're for real yeah you want to keep going okay what's the next question? what is the smallest state in the united states? here's fifty for you? what is this? what are you doing? i just want to help people and have fun you know how much this is gonna help you really how come? i was recently diagnosed with a bong marrow disease so i'm so sorry no it's gonna be okay! i have faith that it's gonna be all right you know god is good how much is it that's thirty dollars man that's blessing thank you very much stop here's a hundred yes, oh my god i hope this helps god busted no no, no god bless you! i've never had anything like this happened before like this stay in touch okay, yeah! i like that all right god bless you thank you! i hope you had some fun today thank you。
16.0万张鸡米 02:48查看AI文稿AI文稿
02:48查看AI文稿AI文稿what's nine plus? nine plus? nine nine plus? nine plus? nine twenty one? yes okay! what's seven plus? seven plus? seven? uh? is that also twenty one yeah they're both one yeah? hahaha what's eighty? five plus? twenty five credit card? one hundred one hundred thirty five? yes one eleven one eleven yeah that's not that bad a hundred how many countries are in the uk? i'm gonna have to pass on that one i'm not gonna lie to you if you had a guess maybe like countries yeah maybe like twenty one yeah maybe like twenty one countries okay all right for sure oh wait no is it no zero right okay no yeah! i'm just gonna i'm just gonna stick with twenty one how many wheels are on 18 wheeler? wait wait isn't it like twelve yeah yeah exactly twelve yeah wait? no it's not what is it yeah? is it okay yeah on an eighteen wheeler it's usually twelve wheels okay yeah how do i know though okay? what's three times three times three? that's not what's three times three times three is it twenty eight or thirty six twenty eight? i think twenty eight which one well three times three is nine and nine times three think is twenty eight yeah twenty eight okay yeah perfect! nine plus nine plus nine twenty something twenty four why am i so stupid what central where are we in we're in the twenty second right yeah? well how do you how do you come up with that how do i come up with that yeah twenty second because it wasn't last century the twenty first what's eighty five plus twenty five hundred and five yes wow what eighty five let's twenty five high i will say 97 what is 85 plus 25 oh my gosh i know 85 plus 25 yeah um five ten five six sixty sixty good job thank you can you tell me what time this is right here five o'clock five or four five o'clock five or four okay um last guess last guess uh one one forty five okay there you go yeah see it's not one forty five。
4.0万William 03:31查看AI文稿AI文稿
03:31查看AI文稿AI文稿今天我们来求一个十分特别的角度啊,三十三度。看过我之前视频的同学可能会说啊,太简单了, so easy 啊, 用太的整个四三 x 是等于 x, 一次方除以一的阶层减去 x, 三次方除以三的阶层加上 x 的五十方除以五的阶层。当这个 x 很小的时候,我们直接用这个代入就可以求得。三十三度等于多少。因为三度等于派除以六十嘛, 所以说直接带入到这个里面啊,三二三度等于派除以六十,后面就不算了,是约等于啊,因为这个数很小, 那这样做对不对呢?这样做在大学里面啊,是勉强可行的,约等于可以,但是在初高中里面肯定会被打个大叉。那如何求这道题目呢?利用初高中的知识我们看一下啊, 三度恰好等于两个特别的角度啊,十八度和十五度相减,大家可以去尝试一下,看看自己能不能解决啊。我们就直接往下说,三二三度等于三二 一十八度,减去一十五度,把它展开啊,终于全变换,他等于三,我们设这个十八度等于阿法十五度等于贝塔展开,他是这样的啊,三,阿法狂闪,贝塔减去 山白茶,空山好把法白茶带进去啊,就是山一十八度, 孔散一十五度,减去三一十五度,孔散一十八度, ok, 那么三一十八度和孔散一十五度怎么求呢啊?在这里跟大家简单介绍一下。三一十八度求法是画个三角形等腰的啊, 顶角是三十六度啊,然后做一条垂线啊,把它分成两半,一十八度,一十八度啊,这是个思路啊,然后就可以求三十八度了,三十五度该怎么求呢?画个直角下面写啊,因为三十五度等于四十五度减去三十度啊,我们画四十五度角,这是直角啊,再画一个三十度角啊, 然后这个是十五度角,这个垂线啊,我们就可以把这个上一十五度求出来啊,这是初中的方法,高中的方法,当然是通过二百角公式或者说挣钱变换的,在我之前的视频中也详细介绍过,该怎么求啊, 大家可以自己先求一下,然后你看一下我的这个结果,我会把视频的衔接放在这个视频的下方啊,让我们继续求这个啊,求出来。三二一十八度等于四分之根号五减一, 一十八度等于四分之四分之十加二倍的根号五开根号。而三二一十五度和狂闪一十五度的直接比较有特点啊,特别对称啊,四分之根号六减根号二,四分之根号六加根号二。 我们带入到原式啊,原式等于四分之根号五减一乘以四分之根号六加根号二,减去四分之根号六减根号二 乘以四分之一和十加二不对,跟号五,所以最后求出来啊,是这样一个式子啊,等于十六分之一, 有没有什么化解的形式呢?没有啊,他不能再继续化解下去了,所以说这个三十三度虽然可以求出来,但是是这样一长串啊, 这个整体的值实际上跟那个派除以六十是比较接近的,大家可以去算一下啊。 ok, 关于这个三三度,我们就分享到这里啊,关注我,让学习变得更有趣一点。
1033火星课堂 04:07查看AI文稿AI文稿
04:07查看AI文稿AI文稿最近看到一个十分有趣的问题啊,要证明三十度是五里数。之前我们曾经分享过如何证明公号二是五里数,还有一些关于五里数的一些运算。今天我们来看一下三十度为什么是五里数啊?首先找到一个跟他最相近的特殊角 三二三十度,他是等于三十度,乘以三,他又是等于二分之一的。而我们可以通过一些方法求出三倍角公式啊。与三二法和三二法之间的关系。 求解的方法有多种啊。之前我们使用过高中方法和差化解极化和差的方法。今天我们使用一下用万能的欧拉公式推倒一下这个关系啊。我们知道 e 的 ic 塔等于 狂闪 c 塔加上 i 乘以十二 c 塔,那么 e 的 i, 三倍的 c 塔等于 e 的 i c 塔的三字方,也就是这个的三字方啊。 展开之后啊,他是狂闪 c 塔的升值方,加上二乘以上 c 塔的升值方, 加上三倍的狂闪 ct 乘以 i 乘以十二 ct 的平方,加上三倍的狂闪 ct 的平方乘以 i 乘以十二 ct。 化解之后啊,他等于 而 e 的 i 三 c 塔,这方式等于狂闪三 c 塔加上 i 乘以十二三 c 塔。对应的相相等啊。你就能够求出三三倍的 c 等于三倍的狂闪 c 的平方,乘以十二 c 塔,减去十二 c 塔的升值方,把这个等于一减去十二 c 的平方带入啊,变成只有三十 c 塔的设置。 最终是三倍的十二,按 ct 减去四倍的十二 ct 的升值方。所以得到十二三乘以十度 等于三倍的十二十度,减四倍的十二十度的三个方,他是等于二分之一的,我们让三十度等于 x, 那么这个试纸就变成了三 x 减四 x, 三次方等于二分之一,花减之后是八 x 三次方减六 x 加一等于零。这是个一元三次方程啊。这个三十 度肯定是他的一个根,那这个时候能不能把他根求出来呢?好像比较复杂,那这个时候该怎么办?有一个定理啊,叫有你跟定,你 这个定理跟四跟法比较像啊。而且掌握了这个定理的话,因式分解的问题一般都会变得很简单啊。我们找到最高次向 x 方前面的系数八,他的因素 有一、二、四、八,找到最低四项一的因素只有一用这个一除以一,用一除以二,一除以四, 一除以八,前面都要加正负号,有八个可能的有你跟啊。有你跟。定理的意思就是啊,如果这个方程有有你跟的话,那么他的有你跟 肯定在这八个中选啊。如果这些都不符合,那么他就没有有你根了。把这些都带进去,发现没有一个符合的,所以无有你根。而三十度又是他的一个根。所以三十度 不是有理数,是无理数得证。不需要掌握有理跟定理的推导过程,只需要知道这个存在,就能够帮助我们解决好多因式分解问题或者球根问题啊。他的根无非在这些中选。 我们只需要看最高次项的系数和最低次项的系数啊,根据他们特点,找到他们可能的有理根,然后一一带入计算就行了。而关于有理根定理的证明,大家可以订阅清华强基专栏,关注我,让学习变得更有趣一点!
498火星课堂 04:30查看AI文稿AI文稿
04:30查看AI文稿AI文稿这道题如果你都不会做,那么你的数学真的是白学了。这是一道二零二二年专升本考试数学真题计算题的第一题,我们一起来看求极限等于多少。那么求极限是有固定的方法和步骤的,在我们的全程班里都为大家进行了详细的讲解,我们带着大家再回顾一遍。 那么求极线的第一步是先把点带进去,看能不能算出来,对吧?那把点往分子取代,这里是零,算以零还是零?因此呢,分母是趋向于零的。 把点往分子去带,把零往这里去带,算以零是零,那这里是一的零四方,对吧?一的零四方等于一,把零往这里去带,算以零还是零,再减去一,一减一还得零,因此呢,分子也是趋向于零的。所以说这道题是一个 典型的零比零的未定式,我们没有办法直接计算,那么我们只能想到第二步去化解。这道题化解是比较复杂的,因此我们不采用这种方法,那只能想到第三种方法,能不能等价替换? 我们都知道啊,这个分母有一个上瘾 x, 对吧?并且这个上瘾 x 是跟这个整体的柿子是相成熟的关系,所以说我们能够把它等价替换,当 x 趋向于零的时候, 上瘾 x 是等价成 x 的,对吧?所以原式就等于分子,我们保持不动,分母把上瘾 x 等价成 x, 那么分母 x 乘以 x, 可以给他变成 x 的平方,没问题吧?现在我们再把点往里去带,你发现还是零比零的形式,对吧?带一点行, 第二步化减也行不通,那只能想到第三步,等价替换。这道题等价替换是明显行不通的,因此我们只能想到最后一种方法是落必打法则,落必打法则就是对分子和分母同时对 f 子求到就可以了,对吧? 那么我们来看,这里是 e 的上瘾 x 求导, e 的上瘾 x 很明显是一个复合函数,复合函数求导,我们首先要把内层上瘾 x 看成一个整体,看成一个整体优,对吧?那 e 的优求导还是 e 的优, 也就是一的上瘾 app 四,但是大家需要注意,复合函数求导不要忘了,对最内层上瘾 x 再求一次,等上瘾 app 四求导等于扣上瘾 app 四,对吧?减去这里上瘾 app 四求导还是扣上瘾 app 四,那么一求导师 零我们就不用管了,再对分母求导 x 平方求导等于二 x, 那这道题继续带点,我们发现还是零比零行不通,那只能想到第二种方法化解, 那这道题化解的话,分子我们可以把扣上瘾 x 是不是可以提出来,对吧?那么扣上瘾 x 提出来,前面还剩下一的上瘾 x, 次方后面还剩下一分母,我们保持不动, 那大家来观察一下,当我们把零往里面去带的时候,分母是零,分子也是去向于零,对吧?但是大家需要注意,我们观察这里有一个抠算引 f 四 这个扣三 x 跟整体的这个表达是是相成熟的关系,对吧?并且我们把零往里去带,这里是扣三也零,扣三也零是等于一的,那么扣 算以零能算出来一个具体的数,对吧?我们把它叫做非零因子,非零因子是能够优先计算的,所以这个地方一我们就不用写了,对吧?那么给他整理一下,当 f 四趋向于零的时候,分子呢,就变成了一的 cx, 四方减一,分模 保持不动。转到这里我们观察分子很明显能够用等价替换的方法,当 x 趋向于零的时候, e 的 x 减一,是等价乘 x 的,对吧? 这里大家需要注意,只要右上角这个方框趋向于零,那么他就直接等价成方框。所以我们来判断一下,当 x 趋向于零的时候,这个方框 sonyax 是不是也趋向于零,那么 e 的 sonyax 减一,就直接等价 成这个方框,上瘾 x, 分子就直接变成了上瘾 x, 分模保持不动。那么当 x 趋向于零的时候,上瘾 x 是直接等价成 x 的,分模保持不动,上下都有, x 直接约掉,最终答案等于二分之一。这道题你做对了吗?
1.6万熊哥教数学
猜你喜欢
最新视频
- 963陈聪
