绘制nyquist图一般方法
我们接着往下看,就是我们怎么来绘制这个奶亏斯特图。首先我们要抓住几个特殊的,就是比如说 我们说我们是要画无穷大到正无穷大,阿米卡从无穷大到正无穷大这个范围,他哦他的呃这个 dj 欧米伽这个复变函数, 呃,他的端点在扶贫面上少过的轨迹。这样的话呃,因为富无穷到零和零到正无穷他是关于十轴对称的,那么我们只换呃阿米卡从零到正无穷就 可以了。如果你要你要补充负无穷到零的话,你把给他翻上去,那么就可以了。 这样的话我们先去抓住两个两头就是阿米卡七零,阿米卡七无穷这两个点。然后我们再去找一些特殊的点,我们看呃能发现什么样的规律。 所以首先我们来看阿米达七零,或者说等于零直接等于零的时候。 对于这样的一个复杂的环节,我们来看他有什么特点。 好,我们看这个表达是当阿米卡等于零的时候,我们可以看到注意他是尾巴是一,注意一定要确认他已经是尾巴是一了。阿米卡 等于零,那么后面的这个有阿米卡的相全部等于零了。所以后面的一整串就是等于一,等于一。只保留了前面的这一项,我们写到这里来。 k 除以 j 阿米卡的六十米, 那么我们可以直接写出他的扶贫和橡皮,就是 a 啊米杆,因为这里 j j 平方等于负一了,所以他对他的扶贫没有没有任何影响,所以他是阿米杆的六次米粉丝。 k。 然后这里所要判断的就是积分环节的个数,我们说积分环节,他的奶溃式特图是负吸轴,他的向平特性是负的额分之派,或者说负九十度。所以有一个积分环节,那么就有 有一个负的二分之派,那么这里有六个,那么他就是负六二分之派。 这样的话我们就知道了。欧米伽七零或者说等于零的时候,他是一个这样子的情况,就是 a 欧米伽 fi 欧米伽是这样的表达是, 所以说低频段它的福值和上角都是与系统的形式有关的,都跟这个 nil 有关,就是 no 是多少很重要,它跟低频段就是阿米卡。其余零的时候,它的一个状态是密切相关的。 接着我们来看一下六不同的时候,他到底 a 和 f 到底是什么。对于菱形系统,我们说六等于零,一二的时候分别是 菱形系统、一型系统,二型系统。呃,对于三型系统,我们之前也提到过,就是比较少会遇到三型系统,因为呃开环式三型系统的话,那么闭环是很难稳定的。 所以对于菱形系统,六等于零,那么我把我们把零带进来,那么 a 零是等于 k, 然后再零是等于零度,因为六等于零。同理。对于一型系统,六等于一的话, 我们看因为六等于一。下面就保留了一个阿米卡,因为阿米卡七零,那么 a 零是区域无穷,然后呃范零,这里一是富的二分之派,富的二分之派,我们看他是什么意思,就是说阿米卡七零的时候,他会趋于他的福 会趋于无穷大,然后他的向位会趋于富的二分之派。 同样的道理,对于二型系统的话,带进来也是无穷的,然后这里是二的话,就是复派。对于六型系统的话,呃,比如说三型以上,那么 他还是无穷的。然后是还是这个表达是负的二分之六派。所以低频段他有这样的一个特性,就是对于菱形系统,妞等于零的话,他会从他出发点,就是啊米卡七零的时候, 他会在这个正式走出发,因为我们说 k 是大于零的, k 大于零,他会从这个正式走出发。呃,至于他之后走哪里,我们现在还 没有去讲到这个点,呃,我们就只知道他从这里出发,他大概的形状会是这样,或者走上面,也有可能这是对于菱形系统。 而对于一型系统,我们来看,他的 a 是等于无穷大,就是非常呃,非常大的一个, 呃,也不能说非常大吧,就是是一个无穷眼的一个地方,然后他的向位是在这里附近,就是在这根富溪轴,他的附近是富二分之派, 当然他在左边和右边,我们还不确定就是他大理会是这样子,就是跟他平行的 无穷眼的地方。而对于恶性系统,他是从这根富的石轴出发的, 就是他,他的向角会是复派,然后也是从无穷演出发。这样的话我们就知道了。对于菱形系统,一型系统,二型系统,当奥米卡七零的时候,他出发的位置分别是这个正时轴,复习轴,然后副时轴, 当然对于三型系统就是在上面,当然我们一般很少会医的。 接着我们来看阿米卡去无从大的时候会是一个什么情况,就是我们还是看之前我们做过的这个例子,就是传递函数是这个表达式,然后 a 是这个表达式, fy 是这个表达式。 我们看 amiga 七无穷大的时候会是什么情况?呃,我们看 a amiga, a amiga。 我们把无穷带进去,因为 呃这里这里开根号出来,就保留一个阿米卡,然后跟一个阿米卡消掉之后,底下就是啊米卡的立方这样的一个接触。那么因为啊米卡区域无穷大,那么 a 是区域零的对吧? 然后我们来看 fifi, 我们这里阿米卡用无穷带进来,用无穷带进来。我们知道呃阿克听进无穷。我们看阿克听进的函数是这样子向下的。当阿米卡去无穷的话,他是正的二分之派, 正的二分之派。我们看呃这两个可以消掉了,一个是负的二分之派,一个是正的二分之派,那么这里还留下了一个二分之派,所以呃他是负的二分之三派,就是他七零, 然后是负的二分之三派就是呃,我们稍后会看到他是呃从正西走减入原点的。 好。我们来看一般情况下奥米卡七零的话,奥米卡七无穷的话,那么 a 奥米卡会等于零。如果下面的分母的接次会比分子要大的话,就会是零。就是我们刚才看到的,因为分母的接次就是他会多一多至少一个奥米卡, 因为阿米卡其余无穷就是无穷分之一,那么他是零。然后 fire amy guy fire amy guy 就是比较 两个接次的差,就是 n 减去 m, 然后二分之派,注意他是负的。就是一般情况下 n 是会 大于 m, 或者说等于 m, 等于 m 的时候,那么他刚好是零大于 m, 就 n 减 m 等于一的时候,就是负二分之派。这是他在无穷的时候。 呃,如果说 n 等于 m, 如果说 n 等于 m, 就是分子分母的接次一样的话,那么 a 无穷会等一个长数,因为呃,无穷分子分母,呃它的接次都一样的话,无穷就消掉了,那么前面的长数就留下,前面的长数就会是 a 无穷。 当 n 大一 m 的时候,起线的终点他都会回到原点。就是这个表达是他的福值都会等于零。并且他的高频段,他的起线是 以什么姿态减入这个原点?是以 n 减 m 数字,看他跟哪个坐标轴相切,减入原点是跟 n 减 m 有关的。 好详细的,我们来看一下。就是我们把这两个狮子还是写在这边。就是 n 带 em 的时候, a 啊敏感会去零,然后 fy 会去。这样的一个表达式。 我们看 n 减 m 等于一的时候,坏无穷是负的二分之派,然后等于二的时候是负派,三的时候是负的二分之三派。所以我们就可以画出这样的一个图。 就是 n 大于 m 的时候,他会减入原点。但是以何种姿态减入原点,就要看 n 比 m 大多少。如果大一的话,比他刚好大一,那么就是负的二份自派,负的二份自派是负吸轴,这里 他就会以这个负吸轴相切的这样一个曲线减入原点。当然我们不知道他是从左边减入还是从右边减入,所以 n 减 m 等于一的时候,他的姿态就是有这两种可能。 同理,对于 n 减 m 等于二的时候,就是复派,复派在这里负的十轴,然后 n 减 m 等于三的话,就是负的二分之三派,就是看他们的差到底是一二三。他是以这样的姿态减入原点的。 呃,要注意的一点,如果说 n 减 m 等于零, n 减 m 等于零,那么坏无穷还是等于零。那么他还是在这个正的时轴。正时轴的话,呃,他可能从上面下来,或者从下面上去回到这个正时轴, 这样的话我们就有了起点。起点。我们说看积分环节有几个,就是他是什么形式的系统。第一,菱形系统,从正式招出发,一型二型、三型系统。 呃,就是他出发的位置,然后终点。终点捡入的位置是看他分子分母的结实,谁比较 高,就高多少。就是 n 减 m, 如果 n 减 m 等于零,就是分子分母的皆是相同,那么他还 会回到这个十轴还是一。如果 ntm 等于一的话,他会从这里回来,从负的西轴回来。二的话是这里,三的话是这里。所以说数数数的时候, 正时轴永远是零对吧?就是正时轴是零。所以对于呃数积分环节, 这里是零数,呃, n 点 m 这里也还是零,就是零一二三这样子数,就是顺时针的数。对于起点, 起点的话,我们就看积分环节的个数。对于终点的话,我们就看分母比分子的接次高多少,高多少个接次都是数零一二三,顺时针这样子数。 好了,刚才讲到了起点和终点。而对于中频段的话,我们是要去计算特殊点来确定,比如说他跟坐标轴的焦点,我们要找到这个焦点的时候,他的频率和敏感的数值, 还有焦点的坐标,我们要给他确定下来,这样的话我们获得了起点和终点, 和一些他跟坐标轴的焦点,或者其他一些特殊点。这样的话我们就抓住了他的首尾,还有中间部分,相当于呃拉网一样。我们提高提高气力,把它 把他给可以,给他拉起来就是可以。呃,通过这几个特殊点,可以把奶亏斯特图的一个近视的图像给他画出来。 好比如说。我们再看这个习题。习题三说下面哪张图是这个系统,他的奶亏式的图。呃,大家也是可以先把视频暂停一下,然后思考一下到底选哪个。 如果想好之后,我们就一起来看一下。我们看这个传递函数 g s。 他有两个积分环节,然后有两个惯性环节。 我们前面提到就是对于他的起点和终点,我们就数他的积分环节的个数和 n 减 m 到底等于多少。 对于这样一个系统来说,我们说这里 s 平方,所以它是二型系统,所以又是等于二的。我们就开始数就是零, 所以正时轴是零零一二,所以他是他是从这个负时轴出发的,就是跟他平行在无穷演出,所以不会去选 b 和 d, 然后 a 和 c 都有可能。 然后我们来看 n 减 m 等于几,因为我们说有一个 s, 就有一次,这里 s 平方。然后有两个惯性环节,那么 n, n 等于四,对吧。 n 等于四,然后 m m。 注意这里 k, k 相当于是零次的。呃,以往有些同学认为这个常数是一次, 一定要注意,只有有一个 f 才算一次。所以这里 n 减 m 就等于四,因为 n 等于四, m 等于零,那么它是四次的,所以我们就 就可以数,就是看他终点是以何种姿态减入原点。就是还是正十轴是零,零一二三四,所以他是跟正十轴相缺减入原点。 所以他不会是 a, 他的答案是 c, 就是我们是选 c。 然后我们也会看到,就是对于这样一个系统,他的乃克斯特图就是这种形状, 因为他是二二二型系统,就是 s 平方有两个积分环节零一二,那么他从这根轴出发,他是跟他这样平行, 然后 n 减 m 等于四,就是零一二三四,以正时轴相切减入原点。呃,如果你 不记得刚才的那个图像也没有关系,我们刚才提到过,对于一个这样的传递函数,你看到就能够写出他的 a 和 fai。 我们直接把 fai 写出来看也是一样的,就是 fai amiga 等于。因为 s 平方一个 s 就有一个负的二分之派,两个的话就是负派。然后两个惯性环节分别是两个给他写出来。 好了,有了这个之后,我们把阿米卡七一零,七一零带进来,那么他是零。因为我们知道阿根廷景的图像是这样子的,一个下来的一个图像,阿米卡等于零的时候等于零,所以 fi 呃阿米卡七一零的时候就是复派,就是这样子复派。 然后阿米卡之一无穷的时候,阿米卡之一无穷。我们知道阿根廷进无穷,阿根廷进无穷的话是二分之派, 所以这里有个二分之派,这里有个二分之派,所以他是负二派。负二派的话刚好是跟这个零就三百六十度是一样的,所以他是这样减入原点的。 所以对于如果大家呃如果忘记了,或者说对刚才我们提到的起点和终点不熟悉的话,呃,你也可以把 five five 写出来。这样的话你做这样一个判断是比较迅速的。 好,接着我们来看。呃,对于绘制奶绘师的图,我们教材给出了一般方法就是 我们先给出,就是传递函数 s, 用 go 美感来代替,之后获得他的屏蔽特性,然后求出他的食品。 就是这边是他的十步啊,一级这样敏感。呃,我们教材是这么写的。我们我们写成 a fiu v, 就是扶贫向平,食平,虚平,这这几个 扶贫向平,食平,息平。我们全部呢把这些表达式给他求出来。这是第一步。第二步我们求出几个特征点,就是起点,终点,还有跟坐标轴的焦点, 这样的话我们把它标在及坐标上面去。第三个是补充必要的几点, 是根据他们的变化趋势和 gjome 卡所处的象限,然后可以做出奶亏斯特图的大 至极限。所以我们换奶馈师的图不要求非常的精确。呃,只要差不多就行了。因为我们我们不会像计算机一样画出非常准确的图形。 而且画奶块式的图我们也不需要,不需要把呃很多的坐标,比如画的很细,比如一格一格一二三这样子去画,我们只是抓住他的大字的图形, 比如说焦点坐标,我们给他画出来,然后如果有间接线的话,我们把间接线的平行线给他给他,这样子做出来就可以了。 呃,有些东西可能会问啊,就是我们我们说我们说一个平地特性 g j 哦,敏感。它是一个复变函数。复变函数我们可以用扶贫和橡皮来 表示,就是 a 和范,他们作为一组已经能够完整的表达了这个频率特性。当然你用优和 v, 就是食品和西品来表达也是一样。 那么现在的问题是,为什么一定要把这四个求出来?为什么我们不只求其中的一组,比如说我们就只求十平和西平一组,因为他已经足够完整的表达了这个负面函数。 或者说我们只求 a 和 fai, 只求他的扶贫和橡皮,我们能否就可以把这样的一个奶亏斯热图完整的表达出来?呃,关于这个问题,我们后面会看到,就是如果说某个 系统,我们给大家,然后你只把 a 和 f 写出来。呃,很多的时候有些特征是没办法完整的表达的。 呃,但是有的时候 a 和 fi 就已经足够了。就是我们后面会讲一个渐进线,如果他没有渐进线,那么我们 a 和 fi, 因为我们知道 a 和 fi 我们之前前面讲过。我们 看一眼这种特殊的,有五个典型环节组成的这样一个系统,我们一下就能够把 a 和 fy 给写出来。 这种情况下可以不去求他的食品息评,因为呃,对于求食品息评算起来还是比较麻烦的,因为一旦复杂起来,你要去算还是比较费时的。呃,很多很多的时候,很多同 同学最开始的时候一算就算错了,尤其是接平方等于负一这一点,就很容易很容易把它算错。 我们接着往下看。我们说绘制奶溃师特图的方法就是三点一线,就是抓住三个点和他经过的象限。所以所谓三个点就是起点,终点和焦点。 就是阿米卡其余零的时候他从何处出发,然后阿米卡其余无穷的时候是以何种姿态减入原点,然后阿米卡等于多少的时候,他会过坐标轴,他的坐标轴到底是多少, 然后他经过了哪几个象限。要注意的是他的起点我们说过就是根据他 有多少个积分环节,就是六等于多少,他是几型的系统。然后来数从正十轴,然后顺时针的数零一二三,看他的起点是从哪里。 而对于如果 n 大于 m 的话,那么他一定会减入原点。他是以何种姿态减入原点,就看 n 减 m 等于多少, n 减 m 等于零 的话,他是会回到正时轴,一的话,他是会以腹膝轴相切,这样减入原点。相应的一二三就 n 减 m 等于一二三四一是我们顺时针数那个坐标轴就可以了。 然后对于呃跟坐标轴的焦点,我们要令 u 等于零或者 v 等于零,这样我们来 求出呃阿米杆他的阿米杆数字,然后再带回去求他的坐标中。另外他经过的象限,我们要去看他的外角到底是怎么样变化。 好,我们来看呃我们的做法是怎么样的。就是第一步我们要把它写成这种尾巴是一的表达形式,因为我们后面要一记这个扶贫相乘相平相加来写出 a 和 fin, 如果不是尾巴上是一的话,我们就呃没办法获得这个 t, 因为我们就直接写这个。比如说对于惯性环节就根号下一加 t 平方哦米卡平方的,如果 t 不对,那么写出来的东西就是不对的。所以千万千万注意。 第一步就写成尾巴上是一的,然后根据扶贫相乘相平相加。我们总是可以把 a 和 fa 直接的写出来。 之后我们有 a 和 fi 的话,我们可以把阿米卡七零,阿米卡七无穷带进来,求他的起点和终点的姿态。当然我们也可以根据刚才提到的起点和终点,他跟 neil 和 n 减 m 的关系来这样子判断。 呃,保险起见,你把费解出来之后,这样子判断也是可以的,就万一你记错了,呃也是可以用费来费缴来验证。大家一定要注意,换来亏斯特图的时候的一个中心就是抓住这个费缴, 你一旦能够抓住坏脚的话,就是能够呃比较容易的把它画出来。 好。这就是之前提到过的起点,我们看等于零的时候,零一二这样子数,然后终点就是 n 减 m, 零一二三也还是这样子数。 呃,要注意的一点是, n 等于 m 的时候,他会是一个常数,会回到这个正时走。 当 n 大于 m 的时候,他会回到原点。以何种姿态回到原点,就看 n 减 m 等于多少。
粉丝434获赞2527
相关视频
 20:49查看AI文稿AI文稿
20:49查看AI文稿AI文稿我们来看第一个例题,就是系统的传递函数 gs 会是这样一个表达式,现在要大家绘制他的奶亏斯特图, 呃,我们看到这个传递函数之后,我们就可以来分析他的起点和终点,因为 s 有一个,那么六等于一,那么他是从负吸轴出发, 就是六等于一,然后 n 减 m, 我们知道 n 这里等于二, m 等于零,那么呃,零一二,他最终会以负十轴相切,这样减入原点, 这样的话他大体的形状我们就知道。然后根据一般的做法,我们就先要写出他的 a, fyu v, 这里我们先来看一下他的 uv, 因为 a 和 fy 我们一下就能够写出来, 我们把 s 用 jome 卡带进去,带进去之后就获得他的平易特性, 之后我们看分子分母同时乘以他的共额复数,然后有 j, 分子分母同时乘以 j, 然后我们整理一下,就可以获得这样一个表达式, 前面这一项就是他的 u, 就是扶贫,他就是他的食品,然后后面是他的西平,要注意这里还有个负号,这样的话我们就把 u 和 v 可以写出来了,然后 a 和 fi, 我们就可以看着他 就能够把它写出来,一一对应 k 和 k, 对应 s, 对应奥秘感。然后这个冠心环节的开根号这里, 然后因为有一个积分负九十度,然后有一个惯性环节负的阿根廷阿米杆,呃,要注意的是我们求得的 uv, 呃,当然你也可以 a 求 a 的时候你用 u 平方加 v 平方开根号,但是求坏的时候没有那么简单的,就是你挨个听进 v 比上 u, 呃,就不好不好去算了,我们就直接用这种方法扶贫,相乘,相平相加的方法就这样子来做 好。接着我们就来看把阿米卡等于零带进来,带到,带到 u, 我们可以看到带到 u 这个表达是阿米卡等于零 的时候,就留下一个负的 kt, 然后带入 v, 因为呃等于零,上面是一个常数,那么他就是负无穷,然后带入 a 和 fi, 依次获得正无穷和负九十度,我们在等于零的时候是九十度,我们来看 这个 u v a fight 表达的什么意思,就是阿米卡等于零的时候,他的 u 是负的, kt 就是他的横坐标是负的 kt, 然后 v 又在无穷眼处,无穷眼处 就是相当于是这么一个点,就是负 kt 是他的横坐标,然后呃 v 是无穷。也这样的话,我们就知道他是有一条这样的间接线的,就是以负 ktj 零点过这这个点得跟这个虚轴平行的一条直线,这作为他的渐进线,呃,当他趋于零的时候,他就会 跟这条线从点,就是无穷眼的时候,是从这条线的那个点出发的, 然后 amiga 等于无穷的时候, amiga 去无穷的时候,我们呃对于 u 和 v 都是零,然后 a 也是零,呃 fi 是因为这里 啊敏感,等于无穷,这里还有一个负九十度,所以他是负一百八十度,所以因为 n 大一 m, 所以他肯定是减入原点,负一百八十度是这里这样减入原点,所以跟我们刚才的判断 是一样的,他从这个负吸轴出发,然后以负食轴这样子减入圆点,这样的话我们就把这个图线画出来了。 要注意的一点,刚才我们提到的问题就是,如果说我们只是把 a 和 fai 写出来,我们没有写 uv 的话,那么我们就不知道阿米卡等于零的时候,因为阿米卡等于零的时候, a 啊,米卡是负无穷,然后他是负九十度, 我们只可能知道他是从负的,他负西轴出发就负九十度,然后再无穷演出,我们就不知道他有这样一条渐进线存在。所以对于这样有一个积分环节的我们,如果不把优和 v 写出来,我们就没办 办法判断这个渐进线就是渐进线作为他的一个特征,我们就不知道如果我们只有 a 和 f 的话,所以,呃,最开始我们提到能否说只是用 a f 这一组或者只用 uv 这一组来判断, 呃,像这种情况只用 a fight 是不行,就是找不到这个间接线,就是没办法去判断它,所以,呃,很多的时候我们都是需要把 u 和 v, a five 都写出来,这样子来判断 才是比较合理的。呃,但是要注意的一点,呃,对于渐进线来说,大家不要 过分的去强调他。呃,为什么这么说?就是很多很多教材不去管这个教 电竞线,因为我们画奶馈斯特图主要是为了第五章用奶馈斯特判进,利用开环的奶溃斯特图来判断闭环的稳定性。而对于这样的一个判断稳定性,这条渐进线是基本没有作用的, 就是他压根没有作用,我们到时候的判断是找这个负一 j 零点,然后看他左边这个奶亏思的曲线穿越的次数,那么他在无穷眼到底有没有间接线,有还是没有?对于这种判断他是没有用的, 所以有些教材就不去管这个间接一线,而是呃就直接画这样一个草图,至于他有没有间接一线,我们不去管他。然后 如果你不去管电线线,你直接用 a 和 find 你就可以知道,因为呃这里 amiga 等于零的时候,那么他是负一百八十度,如果 amiga 会稍微大一些的话,他就有一个这样的一个比喻, 比负九十会稍微更小一点,所以我们知道他是在这个负吸轴的左边出发,那么我们直接这样画一 画,这样我画一条线,就可以画一条线上线从无从严,然后终点是这样点入圆点的,那么你画出这样的一条线,你没有把这根线画出来也是可以的。 呃,但是这门课我们还是去强调他的渐进线,他作为奶亏斯特图的一个这样的一个特征,我们是要求 大家把渐进一线画出来的,虽然他最后在工程上没有作用,但是作为学习的话,我们还是要知道他的这样一个特点。所以将来如果呃遇到有渐进线的情况,大家一定要把渐进线都给他做出来,好,好吧。 呃,然后它是积分环节改变的起始点,就是低频段的一个特点,就是呃,我们可以稍微先讲一下,讲一下他的起始点的一个问题,我们看这个这个这个函数,这个这个系统 就是惯性环节,是 ts 加一份子 k, 那么我们现在给他给他加的一个积分环节,我们说积分环节他是什么积分环节, 他就是从这里复无穷演出发,然后回到,回到这个原点,那么他有一个负九十度的向位, 负九十度的向位相当于是什么?相当于把原来的冠心环节的这样一个半圆,然后顺时针旋转的九十度,就是加上了他那个九十度。 之后还有一个操作,就是他把起点拉到了无穷远处,就变成了这条线,本来是这样一个半圆,然后他把这个半圆旋转的九十度,然后把这个起点拉向了无穷远处,最后就获得了这样的一个奶溃石的土。 所以说积分环节是改变了低频段,也改变了他的起始点。稍后我们会在奶会斯特图的演变详细的区域 说自己点,这里先提一下。好,我们来看第二个例题,就是设系统的开环传递函数,是这个两个惯性环节的成绩,然后试着绘制开环频率特性图,也这样来,快试着图好,我们来看怎么来做。 对于这个我们可以先做一个判断,因为他没有积分环节,所以是菱形系统,那么他从正十轴出发,然后呃 n 减 m 等于二,他也是呃负的十轴减入圆点,这样的话我们可以把大字的图像画出来, 然后 a 和 fi 我们是直接可以写出来的,当然也可以先求一下 u 和 v, 就是我们把 s 用 jia 敏感来代替,获得他的 频率特性,之后呃都乘以分子,分母乘以他的共二,之后就写成这样的表达式,能够把 u 和 v 注意这里有个符号 u 和 v 给他写出来。呃,具体的计算我们不去看了,我们就把这个食指列在这里, 就是 a fiveuv, a 和发是直接可以写 uv, 就是需要这样子来计算,呃,算起来还是有一点麻烦的, 我们重新把它写在这里,然后我们刚才说了,就是你根据 a 发 uv 来判断也可以,然后根据我们刚才的起点终点也可以 就是从正十轴出发,然后以副十轴相切的这样子的姿态剪入圆点,那么从这条线我们就可以看到他是 是有一个焦点的,现在我们要问这个焦点的频率是多少,因为这里是零,这里是无穷的,那么他在中间有一个焦点,这焦点频率怎么来求? 因为这是一个焦点,所以我们知道它是 u 等于零,对吧? u 等于零,然后有一个 v 的字,我们就把 u 等于零带进来, u 另优等于零,那么分母不会等于零,然后只能是分子等于零, k 又不等于零,那么只是这个括号里面的等于零,那么他就等于这个等于零, 因为我们知道阿米卡他是一个正数,因为我们是零到正无穷,那么开根号之后,我们就获得了 t 一乘以 t 的开根号分之一,这样的话我们有了这个阿米卡的数值,然后给他 带到 v 也可以,给他带,带到这个 a 也可以,就是比如带到 a 算出来就是通过计算 把它直接带进来,就是这个表达式,那么这一段的长度就是他,然后他的坐标就是零 j 负的这个数字,这样的话我们就把焦点的平易和他的焦点的坐标值给他算出来了。 好,还有一个特点就是我们说我们找这个焦点坐标,除了 u 等于零的话,还有一个就是 fai 等于负九十度,就是 因为刚好这里这个点,他刚好在负吸轴上,所以他等于负九十度。因为 u 和 v, a 和 f 这两组分别是完整 的表达了这样一个复变函数,所以呃,用优等于零可以算一次。然后这个 fy 等于负九十度,也是他的一个特点。这样的话,我们来看,如果 fy 等于负九十度的话,我们就有这样一个式子, 因为这里都有一个负号,所以两个加起来等于九十度,然后这个怎么来算? 我们说我们有一个这样的一个三角函数,呃,这个三角函数大家可以把它记住,就是 x 听景 a 加上 x 听景 b, 可以等于 x 听景 a 加 b 除以一减 a b, 就是这个 这个三角函数的公式,大家把它记住。有了这个公式之后,我们就把这两个 t 一啊 打 t 二,你敢带进来,那么就是这样一个表达式,我们说阿个清净这样一个函数等于九十度,我们回忆一下,阿个清净的函数是这样子下来的,那么他要这个数要等于无穷大,他会才会等于九十度, 所以他的分母要等于零,他才会是无穷大。同样的也是这样的一个表达式,跟上面是一样的,然后也是求出来啊,一个等于一,除以根号下 t 一 t 二, 这样的话,我们就用两种方法,一个是 u 等于零, fi 等于负九十度,这两种方法分别可以去求出啊敏感的数值,然后啊敏感的数值带到,带到 a 里面之后,我们就可以求解。 呃,关于这道题,就是这样一个系统,他没有没有积分环节,他没有鉴定线, 所以,呃,可以不一定去求他的 u 和 v, 对吧?就是我们可以看到我们只列出 a 和 fi, 然后我们就用 fai 的一幅九十度就找到了这个点, 所以对于这种情况,呃不一定去求 u 和 v, 因为我们前面看到 u 和 v 的整个计算还是比较麻烦的,所以我们只要抓住 a 和 f, 就可以把他的 这样的一个大字的图像和他的焦点坐标都可以给他算出来。呃,是这个例题是可以不用用 u 和 v 的。 呃,然后这里是列出了,如果说遇到遇到这样的问题,我们就直接 a fi, 然后负九十度, fi 等于负九十度的时候找出这个米杆的数值, 然后带进去求出他的绝技,这样的话我们就把所有的耐克斯特图要表达的特征给他抓住了。 好,我们来看第三个例题,就是有这样的一个开环传递函数,现在,呃要画他的奶亏斯特图怎么来做? 呃,对于这道题,大家先暂停视频,把他的 uva fi 给他写出来好吗? 如果做好之后,我们就继续往下看。呃,我们可以大致的判断一下,先判断一下他的形状,就是因为他有一个积分环节,那么他从这个 负虚轴出发,然后 n 减 m 等于三零一二三,最后他是会以正虚轴相切这样子减入原点的,因为零一二三。好,接着我们来看怎么来求他的 uv, 我们把这个狮子立在这边,呃,看起来是有一点复杂,就是 s 用 j 敏感来代替获得他的平地特性,我们详细的就看这个详细的步骤怎么来解他。呃,然后带进来之后,因为有一个 j 分木于 有个锥,我们分子分母同时乘以锥,那么就有个锥平方了,然后后面的两个分别乘以他的共额复数,分子分母同时乘以他的共额复数,就是这样一个表达式。 下面的因为接平方有一个负一,我们把负号提上来之后,你敢保留之后的这两个相乘,留下的这个,然后上面的是造型, 我们把后面的这两个括号的乘出来,乘出来是这样的一个表达式,要注意的是 g 平方等于负一,所以这里 t 一 t omega 平方前面有个负号,然后这个负号是本身所记录的,算出来就是这个表达式。 之后我们看他的食食品,食品是这个 j, 这里有 j, 这里有 j, 等于负一,负一的话负负得正,又还有一个负一,所以他还有负 k 负, 然后踢一加踢二敏感是这个表达是,然后西平的这里就要命 复 jk 照写,然后里面还保留了这一项,写成这样的表达,是这样的话我们把它分开,分开的话前面就是 u, 后面的话就是 v, 这样的话我们就把 u 和 v 给写出来了,呃,看起来还是有点复杂的 好,我们把 u v a five, a five 的话也是一样,照写 k s 是 amy 感,然后这两个是对应过来, 然后因为 k 等于 k 的负角等于零,然后 s 的负的二分之派,这个这个是分别是这两个表达。是这样的话, a 发 u v, 我们都写出来了, 然后我们另啊米卡等于零,我们会看到,就是啊米卡等于零的时候,呃 u 零,我们带进来,下面这个的为零,这个也为零,下面是一,然后它是负的, k 乘以 t 加 t 二括号 是有这样一个,然后 v 零,那么是富富无穷,就给他带进来。我们就知道, 因为这里是等于零,然后这里只有一个欧米伽的平方向有一个负号,所以他是负无穷。相应的 a 和 f 我们也可以写出来。 呃,我们看到这个 u u 等于这样一个长数,然后 v 等于富无穷,我们就知道他有一个间接线,就是 v, 就是 阿米卡。等于零的时候,他会相当于是过这样一个点,那么他的渐进一线就是 这样子,就是一条通过这个点负 kt 一 t 二这样一个长数的,负的,这个长数的接于零点,那么他平行于西轴的这样一个直线,这是他的间接线, 然后阿弥卡七零的时候,呃,可以看出,呃, uva five 都等于零,因为它是简露的原点, 然后敏感等于无穷带进来,因为这个有一个二分之派,各有个二分之派,所以他是二分之三派,就是负的二百七十度,所以他是以正的西轴减入原点的,所以他是这样一个图像有这样一条进进线, 然后是从上往下这样减入圆点的,那么这里有一个焦点,有个焦点,我们要把焦点坐标给他求出来,这样的话我们令 v 啊敏感一等于零,解出这个焦点的平粒值,然后带到 u 里面,可以算出来,他带到 a 里面,也可以算出他的捷径, 这样的话我们就获得了他的耐克斯特图。当然这里 这里我们举了一个特殊的例子,就是传递函数是这样的一个表达式的,然后呃 t 一 t 二等于一到五,然后 k 等于一。我们可以画,用 max table 可以画出他的奶亏斯特图。
52正均 05:16查看AI文稿AI文稿
05:16查看AI文稿AI文稿啊,大家好啊,这次我们来看一下这个就是有积分环节的耐克斯特图的绘制,这个有积分环节啊,他是画起来是比较麻烦的,他有相应的规则, 我们看这个对于一个系统来说,如果是最小香味系统啊,它的起始的这个香味啊,就是积分环节的个数乘以负九十度, 如果是非最小项目系统,那就是积分环节乘以九十度,这个最小项目系统,就是他的这个几点都在左半平面,对吧?就是除了积分环节之外啊,他的这个 几点都在左半平面,就是最小香味系统啊,最小香味系统啊,是是稳定系统吧,对吧? 那我们看这个啊,这个香味啊,你看这个如果是七一,这个是零度了,他零度的时候,七一远点的时候,他有这两种方式,七一负九十度的时候,这两种方式啊,七一负一百八十度的时候,这个样子啊,负二百七十度,这两个两种方式,对吧? 那这个这个终点就是欧米克七无穷大的时候了,他如果分母的接持大于啊分子的话,那,那那这个他的极极限, 这个传递函数的极限一定期于你吗?所以终点位于坐标原点,如果等于 m, 嗯,那那就是一个场数了,嗯,如果画好了之后呢,还要补线,像像这些规则啊,他他都是那个都会有相应的证明,这个呢,我们如果只是为了考试就死记硬背了, 对吧?啊,像这个这个内容啊,我也是从网上看到别的老师啊,觉得讲的还可以,我在这在这里啊介绍,重新重重重复介绍一下给大家啊,这个比如这个例子, 他这里有两个积分的环节啊,这个呢啊也是是替代领吗?他这个就是 啊最小项目系统,对吧?因为这个几点在左半平面,然后把把这个啊,这个系统用用用平利特性表示,就是把 s 用结,我们一个带进去,然后得出来的相应的十步和七步,然后我们那个七一零的时候呢? 我们那个七一零的时候,因为这个分母是零嘛,所以他十步西部都是无穷啊,无穷那那那这个他的政府也就是无穷的,那么他的起始的下 上位啊,这个是因为他等于他的积分环节的个数乘以负九十度,就这里啊,乘以负九十度是最小项目系统的,所以他是负一百八十度,负一百八十度,就这根轴啊,这根轴前面说过,他是有这种方式去于原点,也有这种方式去于原点, 那么他到底是从上面去远点还是从下面去远点呢?这个其实我们很好判断,因为 k 大于零, t 也大于零, 所以我们看到他的虚实部小于零,也就是在这左半周,但是他的虚部是大于零的, 所以他他应该是在上面区域里,是吧?就开大一点,提大一点嘛。这个终点呢,我们看到终点,他就是你把这个我们这个区域无穷大, 这十步西部都是零吗?所以七进于原点啊,七进于原点呢,那么他的向位是负二百七十度,为什么呢?我们看到这个七原点的时候,他可以啊,负二百七十度,他可以这样七进,也可以这样七进 这个终点的二百七十度,我们可以这样认为,你一个积分环节,你把接我们一个带进去,对吧?这有两个接我们一个,那就两个负接,一个负接是一的啊,接的负二分之派,那两个就负派了。然后这里还有个阿克天津的 啊,这个,这个 t omega 除以 omega 其无穷,它不也是一个负瓦文字派吗?所以可以可以这样理解,这个 omega 其无穷,它的终点啊,向位它是负二百七十度,就等于这个分母在接触 是三,这个分子的接次是零啊,一个接次就贡献一个负二分之拍吗?那起点他就必须按照这个来哈,积分的环节的啊,个数乘以啊,乘以负九十度,所以呢?画好的这个那不是在曲线,就他就是这个样子啊,他当然 这个负二百七十度,他是肯定是从这边取进的,不会从这边取进,因为他的这个虚啊,这个十步,刚才已经说了,他的这个十步十步是小于零的,所以按照他的十步小于零,就只能从这边取进 画出来,也就是画出了这这一半,然后要要补线,要补一个这样的线,把它成为一个啊,一一个环形,那这个这样补,它是逆时针转,对吧? 补,补成的逆时针转的这个样子啊,你,你如果这样补,那就是顺时针转就不对了,就这样补啊。像这种这个这个画的缺陷肯定需要很多的理论证明了,这个只是我们把它的规则记下来,背下来。
 21:38查看AI文稿AI文稿
21:38查看AI文稿AI文稿我们接着往下看第四个例题,绘制这个开环系统的奶馈斯特图, 我们可以看到他是 s 平方,就是 u 等于二,那么零一二,他是从这个负十轴出发的, 然后 n 减 m 等于四,对吧?因为上面是零,下面有四次,那么是零一二三四, 所以,所以他是以正十轴这样相切卷入圆点的,所以大致的形状我们就可以知道他是从这边出发,然后卷入 这样子与他相切,与正式轴相切减入圆点的。好,具体我们来看一下, 我们看系统的平地特性,就是 s 用 jobe 卡带进去,带进去之后我们可以把 uv 给解出来, 就是这一项和这一项 gt。 我们不计算了,然后 a five, 我们直接可以写 uv, 就是写成这样的表达式,我们看看 a 的,看 a 啊,那个就是 k, 照写 s 平方是欧米伽平方两个造型,然后 s 平方是复派,两个对应下来是分别是这两个。之后我们看欧米伽等于零,欧米伽等于零,带入 u 带入 负一,那么一个是负无穷,一个是正无穷,然后 a 的话是正无穷,然后角度是负一百八十度就是负的实走, 然后你敢去无穷的时候, uva 都等于零,他是减入原点的,你这个负三百六十度就是零度,零度就是正十轴减入原点,那么可以画出是这样的一个图像, 就是这样,因为 u 是这里附的,然后 v 是这里正的,所以他是从上面上面下来的。 好了,有一个焦点,这边我们可以看到他有这一个焦点,我们看焦点频率的话,我们是另 u 等于零,因为他是在西轴上面,那么 也可以解出来令 u 等于零,刚好是上面等于零,然后很敏感,等于这个数字带到 v 里面,刚好求出来是这个字,然后这点坐标我们就知道。 呃,刚才我们可以看到,其实对于这个来说,我们不并不是一定要把 u 和 v 求出来,就是我们因为他没有电竞线,我们并不是并不需要 uv 这两个数字,所以我们直接写 a five, 然后因为我们知道焦点是这个负的两百七十度,那么把它带进来,带进来一样求解啊,米卡等于这个数值 带到 a 里面,我们就知道这个绝技是这个 a 啊米卡,那么,呃,对于这道题来说,也是并不需要有 uv。 好,接着我们看第四个习题,就是开环系统频率特性是这样表达是,然后当奥米卡等于一的时候,他的频率特性他的橡角是多少度? 呃,请大家暂停一下视频,然后朝高之上计算一下这个橡胶是多少, 如果做好之后,我们就来看一下对于这个怎么做,就是我们知道他的传递函数了,就是 g s 等于一加 s 的三次方,然后分子三,呃,我们可以直接写出他的 角,因为我们要求上角就是 fine amiga, 因为是三个,所以我们依次 t 等于一,那么我们就写这三个,然后我们把 amiga 等于一带进来,带进来,因为阿根廷进一刚好是四十五度, 所以就是负的一百三十五度,这样的话我们他需要平一侧性的橡胶,我们就给他 fai 写出来就可以了。 接着我们看 ct 五,就是某个环节他传递函数是这个表达式,那么现在问奶亏斯特图他的终点坐标是多少? 呃,请大家把视频再暂,视频再暂停一下,然后计算一下他的终点坐标是多少, 如果做好我们就一起来看一下,就是给另一个传递函数之后我们要求他的终点坐标。 呃,当然你可以先把 uv 气除出来,其实我们说没有必要,只要他没有,没有这样的一个间接线的话, 呃,对于我们画呢克斯特图 uv 其实用处不太大,我们直接写出 a five, 就是我们知道一个惯性环节加一个 ejv 分,那么我们就直接写 t 平方 一百的就是一万,十的就是一百,然后赛角阿克廷仅一百好米杆,然后减去阿克廷,这里是十,因为上面是呃分子,所以是正的,分母是负的, 这样的话要求终点坐标,我们就令阿米卡去无穷,去无穷带进来,因为无穷比无穷消掉了,消掉之后就开根号出来,一一忽略不计的话,一百除以十,那么 a 等于十, 然后呃 amiga 等于无穷带进来,都是二分之派,两个都是二分之派,就是阿克天津,无穷是二分之派,两个一相减就是零度,这样的话我们就知道他的终点坐标是十距离, 现在我们问他起点坐标在哪里?起点坐标我们把零带进来,对吧?我们把零带进来,零带进来,这里都是零的,只留下了一,这里零零,那么他就是一追零点,也就是说他在哪块式的, 他的起点是正十轴的一,然后终点是十,那么他是在哪个象限? 是在上半平面,是第一项线还是第四项线?呃,关于这个我们要看坏角,坏角啊,米卡,比如说我们把一带进来前面的大,对吧?我们说阿根廷警,他是一个真函数, 阿根廷仅一百会比十大,所以这个外角是一个正数,所以,呃,我们初步可以判断他的奶亏石的曲线,就是从一出发正十周的一,然后经过第一象限之后回到十, 我们用麦特莱堡画一下,就是写出他的传递函数奈克斯特,然后就出来这样一个图像,呃,在麦克里面他是 把负无穷到零,然后零到正无穷统一划出来了,他就是这样的一个圆,他是起点是负一阶零点,然后是这样一个半圆上去到达这个十是他的终点, 然后富无穷到零是这边跟这个十轴是相互对称的, 这样的话我们就知道了他的整个的耐克斯特的曲线。呃,我们挤这个,呃, ct 的是因为我们要判断一下,就是 n 等于 m 的时候,他是如何从, 因为他刚好是一型系统,这刚好是菱形系统,菱形系统的话从十轴出发,然后 n 减 m 等于零,就是 n 减 m 等于零,他会有 又要回到这个证实中,所以他是这样子。接着我们要问,如果他们交换一下子会怎么样?就分子分母交换一下会怎么样?他从哪里出发? 分子分母交换,交换之后就是这两个交换,呃,然后一比旁边加,等于零的时候,他还是等于一,还是从一点这样触发,然后终点,终点会在哪里? 终点我们交换一下,交换一下就是零点一这里,然后这个两个一交换的话,呃。前面的就比较小了,然后负的就比较大,所以他在下面, 所以他还是从一 j 零点出发,经过第四象限也是一个圆,呃,半圆,然后之后又 回到这个零点,一 j 零点,这样的话我们就知道了,有这样的惯性环节和一节微分,就是 n 减 m 等于零的情况是这样子。 好,接着我们再来看几个,比如说对于这个场地函数是 s 平方,然后 t e s 加一份之 k, 我们看它起点在哪里? 起点,因为 s 平方,那么零一二,他是重复的十轴出发, 然后 n 减 m 等于三零一二三,所以所以他是以正的虚轴减入原点,所以我们就可以画出一个这样的一个图像。 呃,这种 来看,这是我们刚才的例题,就是这样子,从负的十轴出发, ntm 等于四零一二三四,这样子卷入圆点, 接着我们来看这一个,这一个传递函数是这个比上面的多了一个,多了一个这样子。 t 一平方 s 加一,那么他的图像会是怎么样? 我们看起起点,起点在哪里?起点还是跟他一样,就是因为 s 平方,所以从这边出发, 然后 n 减 m 等于几? n 减 m 等于二零一二,所以他是呃以负的十轴减入原点的, 那么我们看他的图像是这样,要注意的一点是,我们这里只有提大于二的时候才 会是这样一个图像,为为什么踢大于二的时候会是这个图像?我们可以看到啊,就是我们等一下会看他的上脚,如果踢一小一,踢二会怎么样?他会是下面的这一只, 就是我们稍后会看他的相角,才能够呃,明白他到底是第二相线还是第三相线? 因为我们要我们说起点和终点,只是说起点在这边,终点也是以这个负的时早减入原点,那么他到底在哪一只?就是在上面还是在下面, 还是会不会穿过这个石走,我们都不太清楚,我们只有把他的外角橡皮特性给他写出来 我们才清楚。细心的同学可能,呃,还发现一个问题,就是我们这边写的是阿米卡区与林正,呃,那么林到底在哪里? 呃,我们现在还解答不了这个问题,我们说我们在这边无穷远处只能标零证,我们还没办法说零到底在哪里,呃,等到第五章的时候我们再也会去谈零到底在哪里,他会在这个证实走这边 我们在第五站的时候再说这个问题,我们我们现在只是知道他是横屏卡,是去领证的时候是这样这样一个点。 好,我们看刚才左边的,左边的这个,我们把快脚负一百八,因为 s 平方负一百八,然后 然后下面的 t 啊米卡的他是一个负的,上面的是正的,所以我们来看这样一个食指啊米卡等于零的时候没问题,就是负一百八十度,所以他在无穷人数就是负的一百八十度, 然后我们看我们取一个稍微大一点的奥秘感,就是零点一,比如六七或者零点零一,稍微比零大一点的,那么我们就知道阿克廷警他是一个真函数, 而这个是会比较大的,至少,呃,踢一踢一是大于踢二的,比如起零点一,比如说踢一等于二,踢二等于一,那么阿根廷级零点二会, 呃,这个是零点一,那么他会比较大,他会比会比较大,就是负的比较大,比如多了五度, 就是负的一百八十五度,那么他肯定是在上方是这样来判断, 然后他为什么会呃付的越来越大?就是比如说这里是付的一百八十,一百八十多,然后大到比如说付的两百二了, 为什么他会这样增大?是因为这个系数比较大,就是他一开始就是他踢二而敏感,竞争不过,踢而敏感,因为踢一比较大,所以他还是会变得越来越富。 但是到达一定程度的时候,比如阿米卡很大的时候,比如阿米卡等于十万,那么他们之间基本上可以忽略不计了。就是他一开始要这样上去,就是角度越来越富,之后的话他会 衰减,他有一个集值,就是会有一个最大值,之后他最后趋于无穷的时候,两个就抵消了,他们都是二分之派,一个正二分之派,一个负二分之派就抵消了,然后他会以这样的姿态 以这个负十轴相切,减入这样的一个圆点,所以他在无穷远处是负一百八,然后这里可能上升的上升到,比如说最大是负的两百二,那么他又下降回去到负一百八,这是他的整个这样的一个过程。 我们来对比一下,如果说如果没有,没有上面的这样的一个一阶微分,他只是 s 平方,然后 t e s 加一,那么他的图像 大体上会是这样,就是我们就是把后面的这一项给擦掉,我们看他的向角啊,那个等于零的时候负一百八,然后因为阿克勤仅是一个增函数,所以他的角度是一直增大的, 就是他他的整个橡角是一直这样增大,增大到这个边负两百七,然后呃啊敏感区无穷的时候,是以跟这个正的西轴相切,这样子卷入圆点的。 我们对比这两个图,我们就可以看到,当我们增加了一个一阶微分的话,那么他就变成了这样的一个一,他的橡胶有一个最大值,就是在这里他是一个最大值,造了之后他的橡胶就又回到了负的一百八, 所以这里就提到因为增加了这样一个开环的零点,就是有这样的一个导权环节,那么起线从第一平段到高平段联系变化的时候,项位是先要滞后,就是越来越富, 到达一个极大值之后又开始减小,减小回呃负一百八,这样的话,整条曲线就出现了这样的凹凸,然后因为 gs 它包含了一个一阶微风,我们称它为倒墙环节,或者叫呃向位超前,它是一阶微风, 这个时候由于向位是不是单调,单调下降的,那么奶亏斯特图就会发生这样的弯曲,这样的话我们就呃清楚了,如果我们上面 加上一个这样的一节微分的话,是会有这样的变化。 好,我们再来看一下教材第一百三十七页的这个例题,就是他现在是 上面上面的 t 是比较大的,那么他画出来的图像就是这样这样的一个图像,因为呃 跟刚才不一样,刚才是 s 平方,这里是 s, 所以他零一,他是从这个负的虚轴出发,然后 n 减 m 等于一,他又会回到这个负的序轴,然后我们这里可以看到他有一条间接线,因为他有一个积分环节,他有一条间接线是 过这个三十 g 零点,然后跟这个虚轴平行的这条间接线, 他画出来的图像就是这样上去,上去,然后注意他是现在是在第四下角这样上去,然后这样子减入。我们可以看一下零到一百的时候的一个情况,就是我们零到零到一百的范围,我们来再看一下, 他是这样上去,然后最后是以这样相切减入零,减入这个零, 他是一开始的向位还是负二分之派,就负九十度,然后 会稍微稍微有一些减小,对吧?就是比如说这里是更小了,更小了,然后又变大了, 是从负的九十,然后可能降到这边负六十负负的三十多,然后又回到这个负九十,是这样的一条线。 呃。我们教材给的给的图像是这样的一个图像,我们可以对比一下。呃,这里画的不太好啊,就是 我们说有了,有了这一个一阶微分之后,他会出现弯曲,呃,但是不会弯的这么厉害, 所以所以这个图画的不太好。呃。有些同学可能会担心,比如考试的时候,考试的时候遇到这种题的话,我们要呃,因为我们是手工绘图,就是用铅笔来这样子绘图的话,能否把这种弯曲描述的 比较精确,呃。一般情况下不用担心,很少会去考这种弯曲的,就是这样子向上有一些鼓起来,又这样子弯的。 呃。因为就像教材一样,就教材本身他自己也画的不是很理想,我们要把这些呃比较细节的东西把它描述清楚的话,用呃徒手去绘图的话是不太合理的。 呃。再比如说,比如说他穿一个整档环节,在下面,我们说整档环节可以在零到零点七,零七的时候他有一个极大的 呃,比如说他串上去之后怎么来描述他的极大值是一个问题。所以很多的时候我们不会不会去作业,考试的时候不会去呃 出一些比较难的,因为我们要徒手去绘制的话是比较困难的。呃。对于比较复杂的,我们以后就直接用计算机直接用 max level 来绘制这样的一个图形就可以了。呃。但是作为 作为一个学习来说,呃先要把基础的概念先理,先理解,将来遇到比较复杂的时候,用计算机来绘制,呃才能够更好更好的理解这个乃克斯特图的本身。 好,接着我们来看,如果交换一下,交换一下,注意他就进入到了第三项线,他不再是第四项线,因为呃下面下面的那个比较大,所以他的角度呃又会负的比较多, 然后我们可以看到他的间距线过的点是负三十这一零点是这样的一个点,然后他也是因为有一个 s 从负的这里 也是这个负的西轴出发,然后又在这里减入,与他相切,减入回原点, 是这样子,就是看上面的梯,下面的梯到底哪一个大, 从而可以判断他到底是位于哪里,位于哪个象限。我们把他的象平特性范尔米卡写出来之后就能够比较容易的判断。
21正均 01:57查看AI文稿AI文稿
01:57查看AI文稿AI文稿各位好,我们介绍一下 next 曲线的一个绘制,然后呢 next 曲线呢?在这个信号系,在这个,嗯,在这个信号系统里面经常用来绘制一个开往船痕的一个 next 曲线,那么用来判断一个系统的一个稳定性, 那么他是根据这个,呃一个开关系统来判断一个闭环系统是否稳定,那么这个用 next 稳定性判距判断返回系统稳定性呢?那么他是绘制欧米卡从零到正无穷的这个耐克斯特曲线,按其包围这个负一级欧米卡点圈数 横和这个开环传函的这个占右半平面的一个起点数啊,那么就是 z 等于加 p 啊,那么确定这个 b 环特 b 环特征方程在什么? 跟着个数,如果这个呢?那么变换系统稳定,否则变换系统不稳定。好,那我们看一下我们怎么来画这样的一个在麦蜡中实现这个来回是这个曲线。绘制好,我们首先定颜色啊,在屏中间先定颜色,那么 那么绘制这个,呃,这个 g s 等于二, s 加一,除以 s 中加二, s 加一,那我们用 my love 自带的一个 x 的一个函数来进行绘制。好,我们实现一下。 好,然后我们共享一下屏幕, 那么这就是呃, my love 绘制的 一个 next 曲线图,然后 next next 经常这个用于判断系统的一个稳定性,那么它是从欧米伽从零到正无穷的一个 next 曲线图啊,那么大家记住,要是开放船。
 17:07
17:07 10:51查看AI文稿AI文稿
10:51查看AI文稿AI文稿这次课呢,我们给大家讲解如何绘制我们的等高线图,前面呢我们讲解了使用 mateltle 绘制的都是二维的,涉及到了两个轴, x 轴和半轴的图形,现在呢我们讲解一个绘制等高线图, 那如何绘制等高线图呢?我们下面看一下这个视力,首先要导入这个模块,接着呢我们创建了一个 x 等于 op 点,拉 xb 式拉 sb 式的话呢,是负十到十一百个点, y 的话呢,也是负十到十一百个等差的点。 那接下来以后呢,我们要将 x 和腕相交的这个点呢计算出来,德高线呢,也 就是首先要计算 x 和 y 相交的点,如何计算 x 和 y 相交的人脸呢?是用 max 格瑞的。那什么是相交的点呢?例如我们现在涉及到的是三个组,首先 有 x 走,有伴走, 还有我们的瑞轴,这个是 x, 这个是万,这个是我们的 z 啊,这个是我们的 z, x 呢现在是一百个点,例如呢我们现在呢画的就是我画的三个点啊,三个点, 麦上面也是三个点, 那 x 和 y, 香蕉 的点, 这些 就是 x 和万相交的点,通过呢满死个瑞的呢进行获取到。那如果我们现在 x 是三个点,万呢也是三个点,他呢生存的就是九个相交的点, 注册的是九个相交的点,根据这些九个相交的点呢,我们计算一个 z, 获取到相同的 z, 把它呢画出来的图形 就是我们的等高线图。 那首先也就是我们需要计算的就是 x 和 y 的相交的点,那我们现在 x 是一百个点, y 呢也是一百个点,使用 max 格瑞的话呢,生成 x 和 y 的话呢,就是一万个点, 一万个香蕉点,我们来计算出 z 的坐标,现在我 z 的坐标的话呢,就是根据 opd sgart, 这是开平方对 x 平方加上万的平方,对着它开平方,计算出 z 的坐标。 使用 cat 方法呢,我们就可以绘制一个等高线图,现在呢我们代版呢进行测试。 绘制等高线图,首先导入模块 mpart matplareapplat splt, 接着呢 apod, 我们要能拍 l, n, p。 接下来我们要创建 x 和 onex, 等于 a, b 点了拉 sbex, 负十到十之间,我们要一百个得差的点, y 呢,也是拉 sb 式 负十到十,一百个得差的点。现在要计算 x, one, 香蕉 香蕉的点,大 x 和我们的大腕,那大 x 和大腕呢,就是通过掉入一个方法, op 点 max pro 的, 他可以就将我们的 x 和万相交的点呢,帮我们计算出来。那计算出 x 和万来以后,我们可以 计算 z 啊,计算 z 这个 z 的话呢,计算的公式不一样,他出来以后等高线,他的图形呢是不一样的, 现在我们的 z 我就等于 op 点是盖它开平方, 怎么样开平方呢?对大 x 平方加上我们的大腕平方,对他进行开平方,计算出我们的 z, 在钓友挑剔里面的 ctrl 这个方法将 x, y, z 呢缠进去,他就可以帮我们绘制我们的等高线图, 发绘制的高限图,例如我们执行 看一下,这就帮我们绘制了一个等高线图。等高线图的话呢,就从我们的高空啊进行俯看啊,继续俯看他一圈 啊,就是现在呢,在同一个圈上面的话呢,他的 z 的值是相同的,也就是我们的等高线,他的高度是一样的, 那曼特拉的内部呢,还可以绘制我们的三维的这个图形, 创建一个十八,绘制三维图形。 那如何绘制我们的三维的图形呢? 哎,看一下这个上面的话呢,跟我们的这个不一样,所以钓物的方法不一样,我们的等高线图里面有 cat, 还有一个呢,和他长得很像啊, 有一个 t, 再看一下这个方法啊,有个 t, 他呢就是把我们的圈呢填充了。 我们看一下这个是 钓友空奥特福啊,不是 t, 是 fx one, 他是将我们这个圈啊进行了填充啊,填充 也是实测的,是等高线图。那如何绘制我们的三维呢? 除了导入我们绘制二维的这个 pwit, 我们要导入这个三 d 的包 s 三 d, 他呢是 mpl tookit, mplus 三 d 里面那三维肯定要准备的,也是三个坐标 xy, 这时候 x 和万啊,他也是有相交的,这个 z, 根据这个 z 画这个三维的图形,主要呢要创建这个三维的这个对象,创建的时候要将我们的 b 梗呢传进去, 我们的这个飞杆画布啊,放在里面,调右 xsplat plus, 将 xy z 穿进去,就可以绘制我们的三维图形, 对吗?继续测试啊,倒入 我们的模块。 首先 mone flogelon, plaplaxplt, 还要倒入三 d 的土,倒入三 d 包 pro, 它呢是来自于我们 mplat kitty 里面的 polat 三 d ampodx 三 d。 接下来以后呢,我们要 创建我们的 xyz 这个 xy 啊, xy 的话呢,必须 有香蕉的这个点。最后呢他和 z 才可以画我们的三维的这个图,我们把这个数据呢复制一下,创建 x 和 onez。 接下来以后 我们要创建 a, x, e, a, x, e, s, i, d 这个对象, 他呢要放一个杯跟啊杯跟,那我们这个画布对象呢?怎么样来深层呢? 通过 rap 交友飞鸽方法 就返回了 杯杆这个对象 xs, 那 xs 呢?调由 plat 去十二分,将 x, onez 把它呢放进去,就可以绘制我们的三维的图形 雕塑继续显示。看一下这个呢就是我们的三维的这个图,他有三个坐标啊, x, y, 还有我们的 z, 而且这个三维的这个图的话呢,在使用我们的 p 二叉五的话呢,可以啊随便的进行旋转。
16第一播放室 03:02查看AI文稿AI文稿
03:02查看AI文稿AI文稿接下来咱们一起来学一下画航向,题里呢,一般他不会给你真航像,他会可以真航像。咱们这道题呢,首先来看一道用石螺经来给航向的 tc, tc, tc 等于 cc 加 v, 二加 d e v 就是四大加之差。本题里呢,罗航像是多少幺 幺二七幺二六啊?嗯嗯,加上继续做,加上罗京时差,再加上自杀。 本题算出来,咱们这个船的真航像是幺二幺。接下来咱们就把幺二幺画到海图上,有两种方法,第一种是用罗金花, 罗金花是在海图上已经有的,咱们只需要用三角,三角板的长边对住罗金花的中心, 另一边找到,在刻度上找到幺二幺幺二幺,来两个连线, 这个线就是咱们的幺二幺。咱们需要把这个航向啊移到这个点上,需要借助另外一个三角板往上移呢,就把它放到左边推, 现在开放好了之后可以往上推了。推吧,推到咱们这个点,这个圆心 现在就可以画腰向下画,就是一百二十一度,长相为幺二幺 方向幺二幺 幺二幺。 接下来还可以用第二种方法,直接用三角板,用三角板的还是一样,首先咱们应该找到幺二幺幺二幺,在哪个位置 找到幺二幺这条线哎。最后用圆心圆心和幺二幺这两条线构成的直线呢,与经线重合, 现在这个幺二幺与经验重合了,现在三角形的斜边就是幺二幺,同样 我们需要做的就是把这个三角板移过去,现在我需要往右移,所以把固定三角板,固定三角板往下边向下移动, 你吧, 现在就是重合了,跟刚才的动作是一样的,你只需要把这条,把这条线画上来, 当你需要画航向的时候呢?高度刚好是咱三角板下边这条线,三个这边线的高度,哎,画幺二幺就可以了,这个是用三角板的方法。
641中运财税 04:25
04:25 03:53查看AI文稿AI文稿
03:53查看AI文稿AI文稿我是建筑学徒,今天呢我们来学习如何在香园空规里面创建一个这样的道路。好,那么我这是完成后的一个效果,好,我再把它撤销回去,我们重新开始。 好,这是我的一个原始地形图,然后这是我画好的一个单线道路的一个图,那么首先我们得到一个原始地形图以后,我们可以观察这里是有标高,有高层点,我们需要把我们的标高识别到相应工会里面,点击地形输入高层 所有 o 方选地形。好,所有的高层呢都已经被识别了,识别了以后呢我们开始创建我们的一个道路,首先呢我们通过 p l 线 来绘制一个我们的一个道路,那么这里呢我是提前绘制好的一个随机的一个路网。好,接下来我们来生成我们的一个道路,道路呢根,根据我们的一个单线道路中心线来生成的,我们点击 道路,这里有个单线转路,那么这里呢可以设置我们的一个道路的板块,有一级路,二级路,三级路,四级路,五级路,六级路是什么意思呢?一级路呢就是单车道,二级路呢就是双车道,三级路呢就是三车道这样的一个道理。 那么这边的断面形式呢,会选择一个道路的宽度,比如说五加四五米的一个人行道,或者是五米的一个道路面的一个宽度,是吧?这样的一个宽度。 好,这里呢还可以设置他的主次干道,一级公路,二级公路,这里好,首先呢我们在这里我们选择二级一个道路的一个板块就行了,我们选择一个二十六米的道路宽度,这里呢我们选择一个主干道确定, 然后呢我们选择这条路和这两这三条路是一个主干道,点击回车,这样道路就生成了。好,我们再来回 试一下支干道粉丝之路,点击我们的一个切换到我们的一个道路板块,我们切换到一个单车道,是吧?我们希望这边是单车道, 他的道路宽度呢是十六米,点击确定好,点击确定回车,这就生成了一个单车道的一个道路,是吧?那么我们希望这两条呢他的路宽度更小,我们希望是十二米,点击十二米就可以了,再点击回车。好, 这样呢我们的道路就可以完全生成了。成,成了后我们再对道路进行一个处理,进行什么处呢?就是倒脚两个处理,点击这里有一个交叉处理 好,这样我们的道路呢就自动形成了一个倒角,那么我们还可以对道路进行一个什么样的一个操作呢?我们可以对道路进行一个标注,点击这里有个道路标注所有标注,然后小数点后三位点击回车,就对所有的道路交叉点进行 一个我们的一个坐标的一个标注好,标注好了以后呢,我们还可以对道路的宽度进行标注,点击这里有一个所有的一个路面宽度,是吧?我们选择零标注一个懂宽度就可以了, 回车,这样我们的道路宽度标注已经出来了。好,那么接下来呢,我们还可以对我们的一个半径进行标注,点击半径再点击回车,是吧?那么我们所有的半径呢也可以标注出来了。好,接下来呢,我们还可以对我们的一个 坡,一个标高呢进行一个标注,那么他标注的原理呢?有两种方式,一种是根据现状标高,就是我们原始地形的一个标高,一种是根据设计标高,就是我们真正 推演一个地形,根据我们的方案设计得到一个标高,这就是设计标高,那么这里呢,我们没有设计标高,那我们根据我们的一个现状标高来进行就可以了。点击零回车,然后小数点后两位。好, 那么我们可以看到我们在实际交叉路点就得到了我们的一个设计标高,是吧?我们生成了一个道路交叉口的一个标高。好,那接下来呢,我们还可以生成我们的一个道路坡度,点击这里点击我们的一个所有坡度, 然后呢设置的方式呢是双行加前后缀来按三就可以了,点击回车小数点后两位。好,可以看到我们的坡度呢,也可以自动生成了,是吧?是不是很简单,很方便,很快捷。好,那么今天呢课呢就先讲到这里,谢谢大家。
115建筑学徒 03:27查看AI文稿AI文稿
03:27查看AI文稿AI文稿我们讲一个应用,例如制作均值截叉控制图,测量目标某零件长度尺寸,抽取一百二十五个样本数据,光二十五组,每组五个样本,这没问题吧? 好,那我们样本抽取方法,一般在一个班次间隔时间内抽取二十五组样本,每组是五个连续生产线是什么意思呢?就是 找我一个半八小时, ok, 我在八小时内抽二十五组数据,那每组五个连续送软件。假如说,嗯,我五分钟隔五分钟抽一次,但我每抽一次要连续抽五个键, 怎么去画绘制控制图呢?好,我们一共有二十五组,就是 k 一 k two, ok, 二十五,一直到这二十五组数据,每组数据,我们每组我们有五个样本数据,那好,我们 均值其差。方法,那我们就先算每组的均值,第一组 x 一八,等于这五个数据相加除以五,这没问题,那第二组就是第二组的五个数据相加除以五,一直到二十。第二十五组数据,五个相加除以五,这没问题,那我们极差怎么来呢? 吉他,第一组的吉他用第一组五个数据的最大值,减去第一组五个数据的最小值,得到了二一, 那第二组就是第二组的最大值,减去第二组的最小值,得到了 r。 同理,第二十五组的最大值减去第二十五组的最小值,得到了极值。第二十五组的极值是 r 二十五, ok, 最后我们要得到 d, 最后我们要得到均值的 均值,也就是这 x 一八到二 x 二十五八的均值,就是说 x 一八加 x 二八一直加到 x 二十五八除以二十五,再均值, 极差的均值就是用 r 一加 r 一直加到二十五除以二十五的均值,这就是我们要得到的这两个数值,这两个数值是用于我们绘制控制图。 哦,看下边这控制图的基本轮廓。好,那我们中间的值就是 x 八,是,我们前面有算过, 上公叉是什么呢?上公叉就是公式,在这边中间中指就是 x 八八,那么上公叉就是 x 八八,加上 a r 二八 r 八和 x 八八,我们的公式在上面已经给出了 重点,就知道我们下工差、上工差,上工差、下工差的值都已经公式都已经有了,那么唯一位置量就是 a 二, a 二等于多少呢? 可以查表,当 n 等于五的时候, a 二是零点五七七,那当 n 等于七大数,这时候可以查表,去去去搜索,当然百度也能也能搜得到。 这个就是均值的控制图已经出来了。极差的控制图呢,这边是中值,就是极差值,那我们中值,呃,上限值就是第四乘以二八, 下线值就是第三乘以二百,那第四第三差不了也能知道。等于五的时候,第四等于二点一五五一一五,第三等于零。 ok, 带进去我们就能出出上线、下线和中值。 知道这个之后我们就可以绘制。呃,我们的控制图,那下一节呢?我会讲一下用 matter 怎么去绘制控制图。好,今天就到这里。
117质量工程师 凯哥哥 03:27
03:27 14:51查看AI文稿AI文稿
14:51查看AI文稿AI文稿大家好,我们来做这个小案例啊,这里有两个小的,然后这边呢还有几个小案例,这里还有几个小案例, 我们都来做一下,用的方法基本上差不多啊,我每个上面呢争取用个一到两种方法教大家做啊,很简单啊,先看到这个吧,这个是快乐公司 的那个 logo, 我们首先可以看到这是一个正方形,七个正方形分别呢排在我们这八这个八边形的边上,对吧?那我们可能最简单的方法就是什么直接画一个八边形啊,对不对啊?我们首先 那设置好一个八边形啊,把这八边形的角度呢,我们调一个二十二点五啊,他就调平了啊。好,当然我们还可以 调频的话,还有一种方法就是删掉这个顶点,那他也可以啊,然后这里呢我们画一个正方形啊,这样画一个正方形, 把它呢放到上面来,然后再把这个正方形呢中心点放到这个八边形的中心点上,拖动,按住 ctrl 键旋转复制一个,然后再 ctrl 加 d, 对吧?删掉这个,删掉里面这个,然后呢再选中他们填上一下颜色啊,去掉轮廓群组一下, 那这个效果就完成了,很简单吗?对不对啊?当然我们还可以使用一些其他的方法,那比如说我们在绘制这个图形,利用八边形做这个 做那八倍镜做,做这个参照的时候呢,做参啊,做这个参照物的时候,我可以使用这个工具啊,三点去,行,那从我从这个点到这个点出发,那然后按住 ctrl 键, 对吧?那就可以绘制一个句型啊,然后再从这里出发,旋转复制 啊,这样刚好这边我就不需要,就不需要再去复制了,对不对?这是用三点进行画出来,可以说应该更简单一点 啊,还有很多其他的方法都可以完成我们这个效果啊,大家自己可以多去尝试一下,我就不再去做过的假设,那我们看到这个,这是那个谷歌浏览器的那个 logo 啊, 平画之后的效果,那我们可以通过什么样的方法来做出来呢?首先我们可以看到这里有几个圆吗?有几个圆我们就可以先画几个圆出来啊,一个圆,对吧?然后呢往外面再复制一个圆,再往外面再复制一个圆,像这样啊, 然后呢这边有条线吗?对不对?那我可以使用画线,那画线工具的时候呢,我可以从这个象限点出发,那往这边水平,按住 ctrl 键水平画长一点也没关系, 然后再从这个点往这边拖出来,那这里有一个过度的阴影阶段,对不对?这样这个我就比较随意的一个角度哈,注意我画的都让他故意画长了 长一点啊。然后我现在选中咱们这一个两个对象,把中心点呢移到这里,按住 ctrl 键旋转复制,注意 看着属性栏上一百二十度呐,一百二十度,然后我们在这个里边呢给他干嘛呢?填填上颜色啊,我们可以使用咱们的 智能填充工具,在这个里面给他填充颜色啊,在这里填色啊,填色的时候,现在我们要稍微要注意一点了,我把这个先给拿开啊,这里 这两天之后,在我们这里呢就经常可能会碰到这样的问题啊,就经常可能会碰到这样的问题,那我们可以把这个 这复制多一点,也没关系啊,那复制多一点,把这个再复制一个出来,就这样 你看一下哪个能填上,那就填哪一个,那对吧?这样就可以填上了,其实我们只需要填一个啊,填一个就行了。那填完了这个之后呢,我们分别给他 填上颜色,那填上一个颜色,这里给他填上一个颜色,然后我们可以再把这个辅助线的可以给他删除掉,辅助线就不需要了,然后呢 这两个图形轮廓也可以去掉,不需要了,选中他们选组一下,把这个中心点呢放到这里来再复制一次, 对吧?然后呢我们分别给他填色就可以了,分别给他填上颜色就行了 啊。其实这个填色在以后我们学习学习了填色技巧的时候呢,会有更简便的方法啊,把外面这个轮廓去掉,里边呢我们填一个颜色,那把这所有的轮廓都给他去掉去, 那我们这个图形呢就绘制出来了呀,对吧?这就是使用了一些旋转并且复制的方法,这两个都是用用了同样的方法给他做出来的 啊,应该是蛮简单的吧。然后我们再来看到灵儿这个文件里面,那这个也一样的很简单,这是一个菱形的,对不对?呃,三菱, 三个菱形组成的一个那个三菱公司的 logo, 那我们可以怎么样先画出一个菱形出来呀?这个菱形教大家画一个标准的用这个三角形画啊,按住可 错键,画出这个三角形,往下面复制一个镜像复制的,然后再给他焊接合并起来,这样一个菱形就出来了,然后我们再把这个中心点呢放在底下旋转一百二十度, ctrl 加 d, 咱们这个效果就出来了啊,就这样,其实我们这个呢,我还可以教大家一个另类的做法啊,一个另类的做法 是什么呢?你可以先做好这样一个参照,然后我们使用多边形啊,绘制一个三边形,在这里绘制一个三边形出来,像这样呐, 然后接着呢我们干嘛呢?接着我们把这个三角形的这个终点啊,那拖到这个底下这个终点上来,那拖到这个点上,然后 然后呢我们再选择我们这上面的点,按一个加号啊,按一个加号,然后他就在这个中点处呢增加了点,我们把这个点呢移到我们这两个点上来,然后我们这个图形呢就出来了啊,多边形 造型的方法呢,可以把它直接造出来,这另类的说法是吧?这个案例我之前在直播的时候呢,我已经 做过了,对不对?其实也很简单,我们可以使用多边形或者是五角星,那先使用这个心形五角星给大家演示一下,啊啊啊,心形 是吧?然后这个五十三的锐度就刚刚好了,然后我们只需要在干嘛呢?只需要把他们给切开了就行了,对不对?切开了,切开的话,我这边呢可以使用 咱们这个刻刀工具来切啊,刻刀啊,刻刀工具呢,我这边有贝萨啊,还有这个两点模式,还有这个手绘模式,那我们分别都来看一下手绘模式是什么样子的,还有啊,应该用贝萨模式,应该更好点啊,贝萨啊, 从这里往下面拉一条线,然后呢到这中心上单击,再到这里呢啊,再到这里啊,这样子 啊,按一下空格洗漱。呃,这里刚刚那个线的问题啊,这个线不好,我们直接用画线吧,因为他那个被撒在那里不是很,他不能够 直接单击画出直线啊,那我们在这里利用这个杯子啊,可以直接单击画直线就会比较方便啊,那我们这里呢可以再画一条线垂直的, 然后得到了我们这样的几块地方啊,得到这么几块地方,然后我们可以接下来在干嘛呢?接下来 我们选中他们的复制就行了,那比如说把这两块内容,那把这两块内容拿出来呀,是吧?颜色我们可以给他填上去啊, 在轮廓可以填一个白色啊,然后我们存储了之后呢,把这个中心点放在这里, 放在这个地方按一个加号复制的时候我设置一个角度,叫多少角度啊?这个正好是七十二度啊,就是三百六十度除以五吗?啊,如果不会算就在这里输入这样三百六除以五啊,对吧?他就可以过来了, 然后我们再按 ctrl 加 d, 是不是效果就出来了呀?啊,那还有很多其他的方法哈,我这里就不详细的说, 在做直播的时候呢,我还教了利用多边形的绘制方法来绘制过,我这里就不再说了。好,我们再来看一个第三第三题这里面啊,第三题 这里两个图,首先可以看到这个好像是那个什么。嗯,微信朋友圈的那个 logo, 是吧, 我们也可以画出来啊,选择多边形工具对不对?那在里边绘制一个八边形啊,八边形的话我们把它角度翻翻一下,可以直接删掉他啊。 然后我们可以再绘制一个圆,从这个中心位置绘制一个圆啊,往外面绘制一个圆出来,然后我们可以再使用画两点线呢啊,两点线,我们从这里 那朝这个角度绘制一条线出来,然后再把这个线呢旋转复制一下,对吧?那这样旋转复制一下,当然其实我们不需要旋转复制这么多,复制一个就够了,那这样子, 然后我们给他这里呢智能填充一下,那么其他的呢就可以不用了,包括这个八八边形都不用了啊,给他填上一个白色的轮廓,然后再给他填上一个颜色,把中心点呢定到这个圆心的位置来,是吧?旋转的时候呢 是四十五度,按 ctrl 加低,对吧?然后就慢慢的给他填颜色就行了 啊,就这样慢慢一步步的把颜色填上,那么我们这个图形呢就创建好了,把这个圆呢可以删除, 咱们这个图形的就搞定了啊,就这么简单。然后我们来看一下这个, 这是那个汽运的一个 logo, 是不是汽运公司的一个 logo 啊?那下一个方向盘吗?那我们怎么做呢?同样绘制一个圆吗?首先外面是个圆,对不对?那我们就给他绘制一个圆,那绘制了圆之后呢, 我们可以看到里边里边这样一个图形,里面这个图形,其实可能有些朋友会想,三角,我们这个正斗边形可以搞定啊,对不对?正斗边形啊,从这个中心往里这样拿一个正斗边形出来,然后再调节一下我们这个啊,往里一拖, 是不是我们这个图形啊?对啊,就是一样的图形。那我们现在把它们加粗啊,把这个线加粗 啊,加到一定的粗细 啊,然后再把他们转一下,把这个轮廓转成对象啊,选择 咱们这个排列菜单里面将轮廓转成对象啊,这样就转了对象,转了对象之后呢,我们 再给他做什么呢?那可以看到这个都没有什么反应,本来是双线对不对?转完之后都是好好的,然后我们要做几个缺口,那这里要做一个缺口对不对?画线呢?那我们可以画一个句型啊,在这里这样画一个句型, 这里做个缺口,然后到这个地方呢也要做个缺口,我们把这个机器拿过来放到这里 旋转的时候把中心点放这里,在这里捕捉到这个点,那捕捉到这个点或这个边旋转到我们这个上面来看,然后可以往上移一点点,因为这个可能有点短, 往上移点,这样子镜像一个,然后移到这里来,那 这里有三个句型,这三个句型呢就可以来干嘛呢?把我们把我们这个圆给修剪一下对不对? 把这个圆修剪一下,但是修剪之前呢,大家先记得把我们这个,把我们这个图形哈,那把这个图形的四个三个角伸出来的这个角呢?先缩回去,那缩到里面去,这样子缩到里面去 啊,然后把他们俩合并一下,合并完了之后呢,我们再来做一个修剪操作,那图形就绘制完成了,对吧?思路很重要哈,我就讲的。
247程门立学 03:39查看AI文稿AI文稿
03:39查看AI文稿AI文稿大家好,这个视频我们利用图像来动态演示,用鱼弦线来画鱼弦汉字的图像。 好在这个图中呢,我们看一下有一个单位圆绿色的,然后呢圆上一点,一通过一点做 s 轴的垂线,这点是 f, 那么在三角形 e b f 中,角 e b f 这个角,他对应的对边是 e f, 那么他的另一边呢,是 b f。 根据余学函数的定义 coss 角,我试一下 coss 角 eb f, 他的定义应该为 b f b b e, 这是余雅涵的定义, 那么我们就把 b f 叫做余弦线,并且 bf 有方向的,和做正选函数的图像类似, 我们要研究的是角 bf 这个角和 bf 的关系,在直角这个戏中把它展现出来, 角 ebf 把它化为弧度,展现在 s 轴, b f 呢,应该展现到 y 轴,但是呢,他和 s 轴重合。那么我们要利用一条直线,就是 yds 这条 四十五度的直线,把它对应到外轴上去。好,我们通过 f 点做 s 的垂线,与外面 s 这条直线求于 m, 那么我们知道 m f 和 b f 是相等的, 然后通过平移 fm 到 f t n 这个地方,我们就知道了 f p, l n 这一条就是余弦线的直。那么在途中这三条红色的线都是代表了余弦的直。来看一下余弦直的变化, 从零开始, 这时候呢,鱼线线 b f 等于一 f, 撇 m 的值也为一。好,这是初始值,就是说扩散零度等于一, 我们开始变化 好,大家可以看到,随着角 e b f 的增大,扩散的直 b f 再减小, 减小,从一开始减小。继续, 当 ebf 这个角大于九十度的时候,余弦线 b f 为负向的余弦值是负值,继续, 当这个角达到一百二十度的时候,库穗为负一于全的最小值,继续, 当一天画到二百七十度的时候, 库线池漂移帘继续。 好,那么这一个完整的周期已经结束,大家看一下。 好,谢谢大家。
89济南冰浩企业店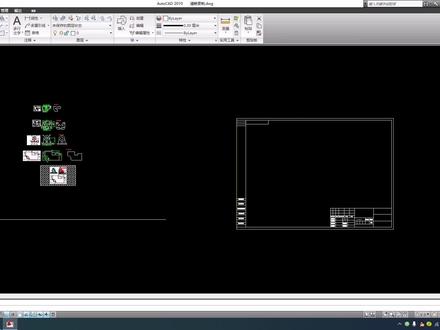 05:19查看AI文稿AI文稿
05:19查看AI文稿AI文稿大家好,我是你的好朋友彤彤。这节呢我们来教给大家一些实用性的一些 cd 里的东西。我们这一节呢要教的就是布局, 我们模型旁边有两个,一个布局与布局二,呃,这个东西用的不是很多,但是呢他是其实要会用的,是情况下这个是非常好用的,我们来看一下啊,我们点击布局一,我们会发现是这样的一种界面, 四周灰蒙蒙的,然后中间一个四口,然后外面是我们的图框区。呃,我们第一步要做的是什么呢?我们可以把这个框的四口给他删除, 也就说我们看不见了里面的模型里面的任何一个东西,这是我们模型的里面东西,然后我们点布局,把这个四口给删除,之后他就什么也看不见了。这里呢我们可以使 使用我们的嗯,一个图框,比如我们这里是一个图纸,我们可以把这个图纸我们 ctrl c 给他复制,然后我们点击布局,然后 ctrl v, 我们可以把这个先把它放在这里啊,把它给粘在这个页面里面,然后我们这里再使用,我们要打开一个四口,也就是说我们在这个画布一样,我们两个开一个窗口一样,我们的快捷键是 mv, 我们点击空格键下面提示我们有不满,或者说任意,我们可以点击任意画一个窗口也是可以的。我们第一个我们选择 f, 也就我们不满,我们发现没有,他就整个给你铺满了,然后我们可以把我们这个图框给他正好套嵌进去。我们这里可以使用 s c, 也就是 我们的缩放,我们点击缩放的基点,这里我们选择参照,然后让我们输入参照的长度,我们点击第一点,第二点也就是我们的这个 a 四图纸的底边,然后我们下面我们选择 p, 第一点,也就是我们把那个图纸正好与我们这个四口大小一样。第二点,然后我们把它给比例给调整好之后,然后我们再把它移动过来, 看到没有,我发现他这个上面这个四口跟我们这个途观是有点区别的,因为是我们这个可能有点问题,是我们图纸的可能有点问题,所以说呢,嗯,他有点问题 不要紧,因为我们这可以调整一下,也就说我们可以把这个图整个就调整好了,然后我们再双击进入我们这个四这个窗口里面,我们发现我们移动的话,在模型里面这么多图纸全部都在我们放大, 然后比如我们这个图,我们把这个图给调整到合适的大小,这样之后我们在右下角啊看到这里有一把小锁,我们把这个小锁给它锁起来,然后我们再点击外侧, 这样我们的点击鼠标轮子的时候,他移动他就会锁起来,如果我们点击进入的话, 他也不会跑,但是如果我们把这个锁给打开之后,我们移动鼠标键轮着的时候,他会跟着我们一块跑,放大与缩小,然后我们这里可以给他锁, 给他锁住就可以了,好让我们跳出来,让我们可以再次使用 mv 开窗口,这一次呢我们不要不满,我们就是这里我们画一个区域,我任意的一个区域,比如我们这里画一个矩形,我们发现没有,我们在这个窗口里面可以继续开一个窗口, 这个好处是显而易见的,因为我们会会图的时候,比如说有些东西我们需要插入各种试图, 我们用到这里我们就非常的好用,我们可以把这里给他点击小锁,把它给锁起来, 然后我们这边的图跟这边的图,而且他们还不是一等比例的,一比一的,我们里面这个可以任意的放大与缩小都是可以的。嗯,这就因为我们有些出图的时候,或者说更有甚者我们后期如果 使用 cd 在 cd 模型里面建模的话,也是可以的。通过一个模型,我们在这个呃里面通过各种四口可以把这个模型可以表达的非常清楚,或者说我们绘制图的是我们粘贴一个 图片啊,或者说一个样式之类,我们放在这里参考,并且我们的绘制的时候可以参考他绘制,非常的方便啊。嗯,这节呢,嗯,我们就先交到这里,至于这个布局后期还可以使用发布啊,很多的东西, 嗯,都是非常非常实用的。我们首先这一节把这个给搞清楚了,我们能够在布局里面把它给开一个四口, 或者说我们能牵套一个图纸进来也就可以了。我们这里如果图纸感觉不合适的话,我们可以继续放大,放大把里面这个有效区域,在这里面我们打印的时候,我们直接可以拉 外侧这个区域,只要一打印也就可以了,或者说我们后期的发布,呃,在发布里面打印,批量打印也都是可以的。好,这节我们就说到这里啊,后面我们就回头继续再说这个布局的其他的一些应用。好,谢谢大家的观看。
2196同同钣金
猜你喜欢
- 3885手绘画者
最新视频
- 4.3万兰小猫





