lineedit怎么和变量绑定

smartly nefe s 软件新功能变量导入 1、 变量导入 smartline 新版本软件支持将 micro win smart 中创建的变量直接导入 win c c flexible smart， 只需三个前提条件便能达到类似国土的功能， 1 win c c flexible smart tv 四、和 stepchi micro win smart 安装在同 epc 二、一、使用 stapci micro win smart 创建项目。 三、已创建 s 七二零零 smart， 连接已经成功导入的变量支持，当 plc 项目变化时再次导入，自动显示差异， 可以按照变量名或者变量地址再次匹配。二、软件操作步骤一、打开 win c c flexible smart tv c 软件，在项目数下通讯电量选项卡 下，单机右键选择从 micro win smart 项目导入变量。二、在弹出的窗口中选择项目的路径文件夹，选择 micro win smart 项目文件，单机打开按钮，随后将显示符号表。 三、从下拉列表中选择连接及匹配规则，选中要导入的符号对应的复选框或选择所有符号。四、单击导入按钮，选中或取消，选中复选框，再次确认要导入的符号。 五、导入成功后，在项目数下通讯变量选项卡下双击左键，确认变量已经成功导入。

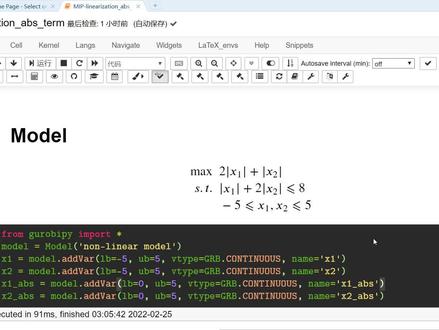
呃，哈喽，大家好，今天我们给大家讲解一下在整车规划中呃，目标函数或者是约束中含有绝对之项的线性化。首先还是希望大家来关注我们的微信公众号运小筹。 好，接下来我们以一个非常简单的例子来讲一下。呃，如果说整车规划中目标函数或约束含有 绝对值钱时的情况下，我们怎么来现现化？首先我们考虑这么一个简单的例子啊，嗯，就是在目标函数和约束中都有， 这个绝对是现实啊，那我们知道 goolby 呢，是可以比较简单的来求解这种问题的啊，是通过他的嗯，广印约束来实现。然后呢，我们来这里来定义四个变量，一个变量就是 x 一和 x 二，也就是 模型中的原来的约束，原来的角色变量。那我们引入两个辅助变量， x 一 abs 和 x 二 abs 分别来表示 x 一的绝对值和 x 二的绝对值，他们都是辅助变量啊，都是角色变量。 然后呢，我们将这个模型写出来，那就是目标函数是两倍的 x 一的绝对值加两倍，呃，一 x 二的绝对值是吧？然后呢，约束是 x 一的绝对值加两倍的 x 二绝对值相等八啊。然后呢，除此之外，我们其实还要加两个辅助约束的啊，这个辅助约束就是我们 用 x 一的绝对值表示了 x 一吗？一的绝对值吗？是吧，那所以说你得加入一个约束，让他去让 x 一的 abs 等于 x 一的绝对值吗？那所以得就得加入一个辅助约束，这个辅助约束呢是通过这个嗯，广运约束来实现。 在古比中的语法就是 id general constant abs 啊，那第一个呢就是你呃绝对值之后的那个变量，这个呢就是原变量，那这个这句话呢，就表示的 x 一的 abs 等于 x 一的绝对值， ok， 那这样的话我们来运行一下，看一下， 那他的解呢，就是 x 一等于五， x 二等于一点五，那目标还是是十一点五？好，这是自由解，这个呢古比呢是求解的是正确的啊。然后呢，我们来看一下我们如何用线性化的方法来给他线性化。 之前我们讲过，一般做线性化的时候呢，是通过引入辅助约束或者是辅助变量来实现等加线性化的，那就是绝对直行式的，也是存在这种 呃，等价现金化的。那首先呢，我们这里的方法就是要引入一些辅助变量，这个辅助变量呢就是 xi 正和 xi 负，我们引入这个 xi 正， xi 负表示 xi 的正数部分的绝对值和负数部分的绝对值啊，也就是这个式子。然后呢我们继续这个我们就能写出来， xi 呢，它是等于 xi 正减去 xf， 是吧？那这里举个例子，如果说 xi 等于零点五，那 xi 正就等于零点五， xi 负就等于零，因为 x 零点五是大于零的啊， 那如果 xi 等于负零点五，那这一项就等于零，这一项就等于零点五，那负零点五就等于零减去负零减去零点五，对吧？那 呃相应的绝对值 xi 就等于 xi 正加 xf， ok， 如有了这个式子呢，我们可以把上面的这个绝对值显示等价的替换成这样，也就是说我们把绝对值形式，我们把绝对值全替换成这个。 嗯，贴好完之后，你就你就可以看到我们的这个柿子啊，就变成了以下的这么两行啊，就前两个就变成这个了， 这里呢，我们是用这个和这个来替换的，是吧？就这这些地方，这是绝对值 x 一，这是绝对值 x 二，这是绝对值 x 一，这是绝对值 x 二。好， 那因为这个还不够，因为我们明明是说 x i 呢，因为我们的真正角色变量是 x i 呀，是吧？是 x i 呀，就是 x 一和 x 二嘛。那这个 x 一和 x 二，他怎么他和这个 xi 一证和 x 一负的关系是什么呢？就是这个嘛，所以说呢，这个呢，我们需要在这写上，也就是 x 把这两个余数加上 x 一等于 x 一证减 x 一负， x 二也是一样。 这引入这么几个约束以后啊，其实还不够，我们还需要引入一些别的约束啊，比如说就是这两个约束。嗯，其实呢， 你确实引入这几这几个约束是不够的啊，只要紧引入后，后面的这几个约束，也就是引入一些 福州别墅啊。呃，这个 x 一 abs 呢，就表示 x 一的绝对值， x 二 abs 就表示 x 二的绝对值。因为我们上面说了，必须有这两个式子才能等等价的替换，那我们 只有这个的话是替换不了的啊，那我们把这个也加进来啊，但是你就得引用辅助约束了啊，引用辅助变量了，我们就得引用这两个，把它写上以后呢，他就等价了啊。 但是有些时候啊，其实你只写前面的四个，就这四个还不够，你还得需要把后面的这四个也写上，也就是说对于一个绝对值呢， x 一的绝对值是比 x 一大，也比 x 也比负 x 一大的，是吧？那这样的话才行， 那 x 二也是一样，把这四个余数加进来才会完全等价，但是有些时候，但是有些时候，我们只需要 这四个就可以了啊。好，我们之后来说一下这是为什么？但是现在我们先把这个代码写一下。好，我们代码呢，就不细讲， 我们这里已经写好了，然后我们运行一下，这里呢也是说，嗯，那假如说我们来验证一下，如果没有这个 x 一的 abs 等于这个 x 正加 x f 这条约束的话，他能不能等价看一下？ 好，那这样一看，哎，他是不等价的，因为你看这个 x 一是负二，但是 x 一的正负分别是三和五，那就是说 x 一明明是我们是想要 x 一等于 x 一正减 x 一负的， 但是他确实等，他是三减五是负二。但是呢，有个问题就是我们还想要 x 一的绝对值，要等于他俩之和，之前不不想等，对吧？说明我们没约束到，没有约束到，我们就得引用新的约束，也就是说 这个 x 一的绝对值和 x 二的绝对值啊，他得等，他得等，他得等才行，把这个约束加上以后，我们再跑一下。 嗯，好，这样的话他就等啊，就是 x 一是五， x 二是一点五，他为什么会这样呢？其实在这还是不是完全完全等价的，只不过这有一个凑巧，因为说三加五等于八，然后我们其实在这约束的这个 x 一的 abs 和 x 二的 abs 必须得在零到五之间，所以说呢，他就没有没有等上，但是无所谓啊，他确实是已已已经成，已经成功了哈。嗯，那如果我们把这四条约束也加上呢？那，那他就是 还是完全等价的，他，他就还是完全等价。 ok， 确实是， 那接下来我们来说一下这个是要怎么推倒出来，就是为什么会是呃这样的一个柿子，柿子呢？啊？我这边已经其实已经推倒好了，我跟大家过一遍， 嗯，这里其实也也说了，就是说我们引入一个呃， xi 的正数部分和 xi 的复数部分，然后我们就能得到这两个柿子，然后我们就能得到这两个柿子，是吧？有这两个可以，嗯，可以推倒得到这两个，这个是没有问题， 这里也举个例子啊。然后呢，我们来想一下，就是这种替换，他为什么是等价的呢？是吧？ 就是如果是等价的，我们需要挣这个，就是说我们带引入了这个，然后我们才能推出这个， 推出下面的表达式，但是呢，我们由下面的表达式能不能推出上面的，如果能推出来的话，那就说明等等价了。那我们这里其实提供了一种证明，也就是说，呃，我们我们把这个前面的两个，就这两个当做一二， 这两个灯三四，然后呢我们把他们加合一下，把他们加合一下啊，就是 三加四呢啊，那就能推出来他俩之和等于啊，两倍的 x 证，那 x 证呢？把它除过去，那就等于 x 证，就等这个啊， 然后呢？三减四呢？是这样的，然后呢我们能推出 x 减等于这个，嗯，然后我们来分情况讨论，如果 x i 大于等于，是吧？如果 x 大于等于 xi 正，哎，那那绝对只有 x 就等于 x， 所以说那这个式子就是 xi 正，他就等于 x， 由于 x 大于等零啊，所以说呢，这个，呃， x 他就等于 max， 另， x 对，因为 x 大等零吗？同样的也可以推出来 x 负，他是 max 零和负 x 啊。同理啊，在小等您的情况下，我们也可以推出来同样的结论，那这样的话，就是我们正推反推都能推过去，那这样的话，就是这种替换就是完全等价的。 好，等价以后呢？呃，其实这里有个小小小，这个，就一般情况下，我们，我们如果把它替换掉以后，我们是默认我们要把绝对值 x， 我们把绝对值 x 替换成这个，嗯，我们把绝对值 x 替换 这个，然后把，然后加约束，让 xi 等于 xi 正减 xi 负，这样的话，呃，那就变成了我们底下的这种情况， 就这种情况。但是这个呢，由于我们这个替换啊，我们并没有显示的表达这个 xi 的绝对值等于 xi 正加 xi 负的，所以说呢，他一般是不等价的啊，一般是不等价，但是在某些情况下是等价的啊，也就是说，如果这个目标函数他是命的话，他这种呢，就就是等，就这前面四个就已就已经可以了。但如果是 max 的话就不行，因为 max 的话，他就是 xi 正和 xi 负都尽量大，他就会最大，也就是说他他会出现这种，嗯， xi 正等于五， xi 负也等于五，但 xix 一等于零的情况下，因为呢，你只 约束的这个吧，你只约束的这个 x 一等于 xi 正加 xi 负吗？那这个五减五等于零，那 x 一也也确实等于零，他也满足你刚刚的这些所有的约束，所以说，但是这个呢，他不是一个可行解呀，对吧？所以说他是有问题，所以说必须得把这两个加进来。嗯， 那这两个加进来以后有的时候也是不太行的，有的时候也是不太行的。在什么时候不太行呢？我们之后再说。但是，但是在刚刚的这个例子中，其实只需要这四个就可以了，就只需要这四个就可以了啊。 但保险起见你还是把这些全部加上啊。但是这个也得看问题啊，一般都是约束加上你的目标函数，还有一些其他约束，他共同导致你要 加哪些约束才等价。就有的时候如果说你目标还是命你，你有的时候你用这四个就可以了啊，或者说你用前两个就可以了。这这都是看是情况而定的。如果说，呃，没有任何其他的约束，或者是说没有其他任何条件的话，你是需要把这些全部加上 他才会等价的啊，他才会等价的。好的，那这样的话就是我，我们，我们之前说了，就是说 我们这里也给了一个例子，什么情况下都不行呢？就是比如说我们 max 两倍的绝对值 x 一，加两倍的绝对值，呃，加 x 绝对值 x 二，但是我们这个约束里面是 x e 加上两位的绝对值 x 啊，你说这个 x e 他没觉得值，这个有绝对值。那这种情况下如果说我们还是用刚刚的说法，就是 我们就是我们只把这个加进来，我们只是把这个加进来， 他是有问题的啊，他是有问题的。嗯，我们可以在这验证一下啊，我们我们可以在这给大家验验证一下，比如说呢？我们在这跑一下这个代码啊。嗯嗯，这个呢就得 啊，这个对，我们我们用用这个代码来跑一下，就是我们的目标还是改成了两倍的绝对值 x 一加 x 二，然后呢是 x 一加两倍的绝对值 x 二是相等于相等于几加？等于八 小等吧，小等零吧，还是小等吧？啊？对，小，我们改成小等零吧，我们改成小等零。然后我们来试一下这个 能不能行啊？跑完以后看一下啊，他这个值是五和负五和负二点五，他目标还剩的是十二点五， 然后我们看一下我们只加这几个约束，这也就是说我们只把这个绝对是 xt 换了，然后呢再把这个呃 x 一和 x 二的这个关系带进来，我们不加 abs 约束。我们来看一下这个情况什么样？ 这就是前面的几个，后面这个呢是两倍的 h 绝对值 x 一加 x 二绝对值 x 一加两倍绝对值 x 等于零。然后呢 x 一等于这个减这个 ok， 那就只放这两个 ok， 只放这两个。我们来看一下他的纸会是什么样？好啊，可以看到不对 是吧？可以，就是我们刚刚说的他就会出现 x 一确实等于 x 一的 pose t 减去 x 一的 next 五减五得零吗？但是呢， x 一却不等于 他俩 x 一的绝对只等于零，但却不等于五加五啊，所以说这个的话就不等价，就是不等价的，就是不等价。但是我们来看一下，如果把这个 x 一的 abs 加上 x 二的 axe 的 abs 等于 xe 的 pose t 加 xe 的那个 t， 这个加进来，他等不等加呢？看一下 啊？这回我们来看一下，这回的话他就等价了啊，他他他就等价了，因为呢， x 一等于负五，那 x e 的 negative 等于五是吧？那这个确实是。那 x 一的绝对值等于五是吧？那就， 嗯，零加五，然后 x 一呢，他等于 x 一的 poseto 减 xe next 零减五的负啊，这个是没有问题，那如果把这几个加进来，那，那就可以了啊，就这种情况下，他是把这个加进来就已经是等价了啊，你不能只加这两个。嗯， 但有的时候啊，你是需要把这几个也加进来的，我只是说有的时候啊，就这种情况下，这种很很多时候呢，你都是，你都是需要经过分析你的约束的，并不是每一个都这样，有的时候呢，就是那样就不会完全等价。好吧， 那另外还有一种比较简单的现象化的方式啊，我这里也说一下，也就是说这种 就是如果你的目标还是是命的话啊，你的目标还是如果是命，然后你命绝对是 x， 那这个时候呢，线下方式就非常简单了啊。那那就是 我引入一个辅助变量 y， 然后呢，让 y 大于等于 x， 让 y 也大于等于负 x， 然后命 y， 这样的话就一定能够等价。先先画，因为呢，它是用目标函数以及约束共同 导致了 y， 他就等于绝对 g x 啊，那这是这是共同导致的啊，但是在这个例子中， 但是在这个例例子中，你是不能这样线下画的，你是不能写这个的，你比如说你在这写一个 x 一大于的，呃，这个这个绝对值 x 一的绝对值，比如说你用万一来代替万一大于等于 绝对值，呃， y 一大一点 x 一， y 一大一点 fx 一，然后你 max 二 y 一加上 y 二，那这样的话那就没边了啊，那就没边了， 那这个麦克斯就直接无界了，对吧？因为 y 一 y 二他，他比 x 大，比副 x 也大，那他可以取一万，一千一百万，什么都可以啊，是不是？那就无界了？那这种情况下你的现金化就不对啊， 所以说呢，这个绝对值得现象化，一定要根据实际情况来现象化，一定要灵活用，他其实不是唯一的，他有好几种方法啊。那总结来看就是呢，如果说目标还是为命，那你是可以视情况而定，采取这种比较简单的方法。如果是 max 呢？ 那我们就建议你用这种引入这个正负啊，正负部分的这种，呃，现情况这一整一个引入正负部分的这种方式来给他实现现象化啊。那这个时候具体的情况呢，你是需要去 你看看这些这些约束你有没有必要加，如果说不等价的话，你就得把这些东西全部加进去，他才能够完全等价。好吧，那这就是我们今天要分享的这个绝对只是线性化，这部分的内容还算是比较细致吧，所以说得需要大家去亲自体会，亲自试，好吧，好，谢谢大家。

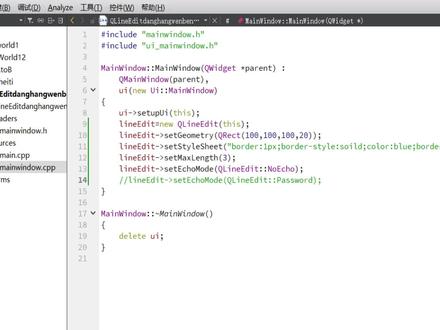
呃，各位好，我们现在来实现多行文本的输入，用 co test id 提示实现多文本书，那么一样的，我们还是在这个，嗯， q t 下去建一个项目。 好，那么一样的，我们在在这个 同音键下， res 包含 金库，包含扣呢，按电梯图文件，那么写好过后，在 cpu 文件下啊进行除函数函数的复写， 那么这里不要忘了要对 ident 实现这个。嗯，声明 for it 多横对着前面有个线，好在视频虚伪的念一下，那么继续书写 啊，我，我们已经在图文件下面进行了声明，那我们这里就可以直接写空键了， 多好。 那么我们进行了空间的创造，然后就对空间的位置和大小进行 我和 city 位置 ok， 然后对它的文本内容进行书写， 比如说第一行，那么这里换行 p r， 这样好，好，我们也可以再加 b r 第三行。好，这里预想中应该是有三行的一个输出， 我们运行一下 啊，嗯，这里我看到的运行结果，这个宽度的高度有点低，我们加加大一点。 好，我们来看一下运行结果。 好，可以看出这个这个多行，这个 b r 没有起作用啊，我们看一下什么原因。 b r say test 谁开始 第一行？ p r q 这个字是创业红吗？