假设增量法技巧
粉丝286获赞2424
相关视频
 01:51查看AI文稿AI文稿
01:51查看AI文稿AI文稿我们今天来学习一个新方法,叫做假设增量,今天我们不仅仅教大家方法,还教大家怎么去估算它的误差。好,这道题的话,我们观察一下,是算一个四八七零除以一加百分之十七点六,再乘百分之十七点六,对吧?但我知道大家有很多计算的方法啊。今天呢,我们来说一下假设增量,我们就假设它的增长量 等于八百七,对吧?那么它的基期值就等于四八七零,减掉八百七多少呀? 四百对吧?好,那实际上的增量呢?我们估一下啊,那是不就可以用这个四千去乘以十七点六?注意哈,这样是估出来的增量。 好,我们选估 a, 那 就等于四六二十四啊,然后四七二十八,三十啊,一四得四七,你算出来的估算值是不等于七零四呀,对吧?大家会发现 七零四 a、 b、 c、 d 是 不?没有这么一个选项,对不对?那说明有误差呀,误差是多少?我们设的是 八七零,对吧?估的是七零四,那实际的呢?啊,需要做一下误差分。误差估算对吧?啊?那实际的就等于七零四,加上他的误差,对不对啊?因为实际上他应该在七零四到八七零之间。好,误差是多少呢啊?误差就等于八七零减七零四 啊,再乘百分之十七点六,除个一加百分十七点六啊,注意下这坨,哎,是不是就是一个一百六, 对吧?一百六乘百分之十多,那也就说再除以一加这个这坨,大概数就是十到二十之间吗?对不对?大十到二十,又或者说你们再猜大一点二十多,问题也不大,对不对?所以他只比七零四大十多到二十多,对不对?那答案不可能是 a, c, b, d 又不可能大到 d 去,那答案不就二 b 吗? 好,各位,假设增量法哈,当大家不太会用百分之它的 d 去,那答案不就二 b 吗?好,假设增量,大家学会了吗?
83杨过数资 08:56
08:56 03:18查看AI文稿AI文稿
03:18查看AI文稿AI文稿假装妹留三位,五百五百的百分之六点五,这个数应该等于三十二点五,对吧?三十二点五,让他是三十三,我知道,多给师傅点。那后面这边十三,这边一,差不多就这么个数。前期是五幺三,变化量是三十四,你算是这两个数吗?好,保留四位。保留四位试一下。 五千,那就是三二五减三二五,这个数等于一四八,一四八的百分之五是这个七点几,那我是给他八,那这边是一四零,对不对?所以前期是五幺四零,变化量是三三三,这两数应该是非常准的吧。 除上一点零六啊。五幺三九吗?差,差了个一无所谓,差个一无所谓。这个数三百去掉一位三百的百分之十三 是三十九,还剩二十二十到百分之十就直接给你二,这边十八,他比百分之十稍微大一点点就行了。所以前期是三幺八,变化量是四十一,你算是这两个数吗?误差多少能接受, 几十都能接受,几十都能接受。你知道这个数的百分之一是三十六,所以只要有个三十二三十的误差都能接受。别说一二了,别超过百分之一都能接受,那这个数他的百分之一是五十四,你别超过五十四的误差基本都能做对。用四位算一下四位一回事吗?三千三千的百分之十三就是三九零, 那还剩多少?还剩一个二零三二零三,他的百分之十是二十,这边是二十的话,这边就是一百八。二十他的。呃,再大一点给他二十二,这边一百七十八,那差不多了。二幺三幺七 八和四幺二,三幺七八和四幺二,对不对?现在你也不用太着急,误差到底留多大呀?之后咱们做题,你就知道误差可以有多大了。绝大多数用甲醛分配,在这一步都是略的一个状态, 可以选了,可以选了,为什么?假设文没好?他第一步基本就能选答案继续了啊?这个数,哎, 两千,这边就是五四零,所以是幺二六幺二六。太好了,这边是一百的话,这边就是二十七,还剩个一,谁还?师傅还呗。九十九,前期是二零九九, 变化量是五百六十七,是不是这个数?我的同学们应该非常准,对吧?因为第二步还非常的好,算是吧,二零九九点二,就差一个零点 点。嗯,二幺零零行不行无所谓啊。这个时候还送假设分配,这边七百多,分了一个一百一十七,一百一十七,把它当做三分之一啊。这边是三份,这边是一份,那大概一份是三十, 这边是还三十,这边还九八十七,差不多这样,因为他要比三分之一大一点。那前期就是一九幺三,变化量是六七零,你是这个数吗?同学们, 二十七咋出来的?一百的百分之二十七不就是二十七吗?一百的百分之二十七不就是二十七吗?对吧?哎,符号别忘了啊,分多了第二步要还别忘了啊。
6716花生十三-四海公考 04:20查看AI文稿AI文稿
04:20查看AI文稿AI文稿各位局长好,大家可以看一下这道题目,他只有百分之四十的正确率,有兴趣的同学也可以暂停视频尝试一下。 好,我们先看一下题啊,就是二零一七年夏粮产量与二零一八年夏粮产产量相差多少?数据我已经标出来了,在就是划线的位置,其实就是一个求增量的问题嘛,他说减产百分之二点一,可以观察选项,这选项 距离就是选项差距非常非常小,特别是 a、 c 跟 b、 d 都只差了二。如果说我们正常做的话,不管你是呃假设分配也好,或者是就是直接直除也好,都就是要算的比较仔细,才能选到正确的答案。 然后今天我想讲的方法就是,呃,在选项差距很小很小的情况下,就是类似于这种情况,只差只差几,只差二,只差呃一点点的话,我们可以把选项就是反向带入进去,我们就假设选项的这个这个值就是它的增量, 然后求出他的基期,然后再根据他的这个增长率算出准确的这个增量。比如说我们观察一下这边都是二百八八十九到二百九十八,大概都是这个区间嘛,我们贷一个好算一点,贷个三百吧。 那,那他这个基期他是多少呢?他注意是减产百分之二点一,那我们基期要加上三百,就是一四一七八,然后再乘上一个百分之二点一, 嗯,百分之二的话是二八三点五, 然后还有百分之零点一的话就是一个十四,那算出来的话就是二九七点五,二九七点五的话,我们只能选到一个 d 选项, 就是你即使,嗯,即使你就是带了一个这个最小的二二百八十九的话,因为二百八十九跟二百九十八也只差了一个九,反应到增量里面的话,九的百分之二点一,也就差了一个,呃,零点几吧,对,最后这个结果也没有影响。 这个方法我觉得是,就是有些像这种就是差距很小很小的题目,你看它正确率只有百分之四十,有时候真的可以派上很大的用场。 我们再看一道题好,也可以看到就这道题的题正确率也只有一个百分之五十四。那为啥他这个正确率这么低呢?其实识别上也很好识别啊,他说比上年增加多少,就是一个求增量的题目,数据也放在这里就划出来了, 主要注意看他的选项,他的选项你看 a 跟 b 两个只差了一个七, c 跟 d 也只差了一个四十二,对于一万四千多的一个数,然后增长又是一个十几,他差距这么小的话,确实如果用,不管是用直图也好,假如分别也好,精度要求就非常非常的高。 嗯,因为这题是 ab 一 组,然后 cd 一 组,我们可以先分组,然后再分别,看一下是 ab 里面选还是 cd 里面选。 用假设分配的思想,我们先看一下,如果是一万的话,那就是增量是一千七,一千七的话还剩下一个两千五左右,两千五左右的话,我们当他是一个两千多的一个数吗?就三百四增量多一点, 三百四加上一千七的话,就是一个大概是两千零四十多一点的一个数,那绝对到不了两千四百多。所以 c、 d 不 对,然后 ab 里面我们选的话,我们带一个数字进去吗?我们取个中间数吧。我们带个二零七零, 带个二零七零的话,他是减一下的话他是一二一九五,然后再乘上百分之十七, 一二一九五,一二一九,感觉不是很好,算你就是当然是一二二零零吧,一二零零的百分之十的话是一二二零, 然后百分之七的话是二十四八五四,那一加的话就是一个 两千零七十四。那我们是不是就直接可以选出这个 a 选项了? 好,今天的分享就到这里了。呃,如果大家还有什么问题的话,也可以在评论区一起讨论一下,我们明天再见。
34灰太狼 14:31查看AI文稿AI文稿
14:31查看AI文稿AI文稿本今天再将假设法再讲一下,之前第一个视频讲的比较详细啊,把原理什么都讲了,然后今天我打算从另一个角度来讲一下假设法, 今天讲的还是有选项的,求增量的,然后我们在假设的时候是根据选项结合选项来假设的,我们一般假设的是选项中间的一个数, 这样子基本上你假设出来基本上一步就能得出答案了。 那我现在就拿下面的题目来讲一下,第一个限期是七百八十五,增长率是二十八点九,先看一下, 像我们在做题的时候,一定第一眼要先观察一下选项啊,你看选项差距有个二三十,对这七百多多的数来说,二三十的一个差距算挺大的了,所以这个率当成二十九来做都没问题。 那么可以假设多少啊?是不是肯定要把这个尾巴给八十五给他消掉啊?那看选项基本上都是一百多,那就假设增量为一百八十五,那是不是反推出他的机器?我们应该假设六百啊, 那六百按二十九个点去挣扎,六乘以二十九是不是一七四?那六百加上一七四是不是七七四啊? 那现在离这个七八五还差了个十一啊,对吧?是小了对吧?那说明机器是估小了,实际要比他大,那增量自然也要比一七四大。那首先 a 选项是不是排掉了? 那你看现在第二步只差了个十一啊,这十一里面一部分是增量的,一部分是 g 七的啊, 那你就算十一全加在这个增量上面,他都到不了西亚西跟地是不是排掉了,就只有一个币了,是不是你看一步就得出答案了?我们假设的一百八十五在选项的中间,他基本上是位于选项的中间啊, 所以基本上我们只要算第一步,第二步再利用一个极限,基本上答案就出来了。那为什么有的时候需要第二步啊?那就是因为你第一步你假设的数不准啊,你不是结合选项, 根据选项来假设的,你可能假设一个是两百八十五,你看两百八十五,是不是肯定不在选项中间啊?那这样子,你看你的机器就是五百五百乘以二十九,那这算出来是一百四十五,那五百加 加上一百四十五是六百四十五,你看离七百八十五还差了个一百四,那你看第二步误差是不是非常大?这就是因为你假设的不准啊。如果你假设的准的话,基本上一步答案就出来了,不管选项差距近还是远,基本上一步都能得出答案。得不出答案, 那是因为你假设的不准,不是根据选项来假设的。然后第二题 限期是一三二七,增长率是四十五点二、看选项啊,三百七三百九,选项差距二十,这差距算挺小的, 因为一千多的数,差个二十算挺小的啦,如果对直除的人来说,那就挺难的啦。那根据选项我们可以假设多少啊?是不是尽量把它尾巴二十七给它消掉啊? 那你看三百多四百多,如果假设三二七,是不是他肯定不在选项中间啊?那是不是可以假设个四二七啊?对吧?他比较接近 d 选项啊,但是差不多也是中间, 他会比中间误差更多一点点,但是也是在选项中间啊,对吧?你看,那么反推出 gc 是不是应该假设九百啊? 九百乘以四十五点二啊?那算出来这个增量是多少啊?九,他是一个好数字啊,九是等于十减一啊, 十个一是不是十倍跟一倍的关系啊?那这九百是不是就是一千减去一百啊?一千乘以四十五点二是不是四五二啊?再减去一百一百四一千的十分之一啊,所以小数点往前推一位就是四十五点二了,那再减一下是不是四零七啊,对吧? 那你看九百加上四零七是不是一三零七啊?你这个真实的限期一三二七是不是还小了个二十啊?那说明你的机器是不是估小了,实际要比九百大,那增量自然也要比四零七大。那首先 a 跟 b 是排掉,你就算二十全加在四零七上面, 他都到不了 d 选项,是不是直接选 c 了,对吧?你看假设的准的话,基本上一步答案就出来了,一步再结合一个极限,根据选项结合一个极限,答案就出来了,那这样子自然就很快了。 好,下一题限期是一九八二,增长率是三十七点九啊。看选项选项,最近的就是西跟地,五八是跟六幺幺差了个二十多啊。二十多对将近两千的数来说算是差距很小了,就一个点, 那用直出肯定算的很麻烦。这题可以利用分数法三十七点五,但是今,但是现在我们只将假设法, 那根据选项我们可以假设多少啊?都是五百多六百这样子,那是不是首先我就把八十二给他消掉,那就假设个五八二,那么你机器是不是就是一千四啊? 一千四按三十七点九去增长,这三十七点九直接当成三十八来做就好了。那这怎么算啊?你可以三十八当成四十减二啊,那四十乘以前面一千四就是五百六啊, 两个点乘一千四是不是二十八啊?那减一下是不是等于五三二啊?那一千四加上五三二是不是一九三二啊?比这个一九八二是不是还小了个五十啊?那说明你的增量是不是要比五 三二大?那 a 选项是排掉了,你就算五十全加在这个五三二上面,而且实际上肯定要比五十少啊,对吧?是不是要小于五八二啊?西跟地是不是排掉啊?所以就选 b 了,对吧?你看你假设的准的话,基本上一步答案就出来了,刚刚这三题双式选项差距 不算非常小的, 然后这是后面三题选项差距会越来越小,然后先期一六二七增长率四十七点四,看选项五零四五幺三五二三差距就死了。 那根据选项,我们是不是首先你看肯定是五百多啊,那是不是肯定是要假设五百多啊?你看正好 尾巴五二二七是不是在选项中间啊?那,那我们就正好可以假设五二七了,因为这样的年纪,其实一千一啊,他好算啊,一千一他等于一千加上一百啊,是十倍跟一倍的关系啊,可以利用错位相加啊。那一千一按四十七点四去增长, 那是不是四七四加上小数点往前推位四十七啊,那就等于五二幺啊,对吧?那一千一加上五二幺是不是一六二幺啊?比一六二七是不是小了个六啊? 那说明你的机器增,你的增量是不是要比五二幺大?那 a 跟 b 是排掉了,那六全加上去都大不到 d 选项是不是又选 c 了?他这个六里面是大部分都是机器的,少小部分是增量的,所以他就算全加给这这这增量, 他肯定也是加不到六的啊,对吧?另一个极限他肯定要小于五二七啊,对吧?所以 d 就排掉啊,所以肯定就选 c 了,对吧?你看,不管选项多近,只要你假设的准,基本上一步答案就出来了, 然后在下一题限期是二七八二,增长率五十四点二。看选项啊,九七三九七八选项差距就五啊,这个应该算挺小了吧。 那首先都是九百多,那肯定是质量肯定是假,是九百多了,看选项,哎,八十二正好在选项中间,那是不是应该假设个九八二啊? 那你的七七是不是就是应该是一千八了?一千八按五十四点二去增长,这怎么算?十八也是一个好数字啊,十八他是等于二十减二啊,可以利用错位相减啊。你看,其实 很多数字他们中间都有很很强的一个逻辑关系,如果你只是去直除或者列数,列数字去乘法的话,你肯定不知道原来数字之间他还有这么巧妙的一个关系啊,对吧?你肯定是分析多了,这些关系你分析多了,那就很熟练了, 你看到他自然就想起来用了,但是你都没这样子去思考过,那你这样去想,你肯定想不到啊。 那,那这个一千八就等于两千减去两百了,两千乘以乘以五十四点二,是不是就是五十二的两倍一零八四啊?那后面 是前面的零点一倍,那小数点往前推一位就是一零八了,你减一下是不是九七六啊?那一千八加上九七六是不是二七 七六啊?比二七八二是不是小了个六啊?那说明你的增量是不是要比九七六要大?那 a 选项排掉六就就算全加上去,他也才,而且是肯定加不到六的,是不是肯定要小于九八二啊? 那 c 跟 d 排掉就选 b 了,看对吧。不管选项差距多近,基本上一步答案也就出来了,差距远更不用说了,只要你假设的准,基本上一步答案就出来了。 还有一题, 可能很多人说就是,如果假设的不准,该怎么算啊?不是,不是假设的不准,而是你假设出来的这个 g 七 不太好算的时候,我们应该怎样算啊?那么可以利用拆分的思想来算啊。看这一题啊,先期是 二幺六幺,增长率是六十二点一啊,看选项都是八百多啊,那肯定我们假设八百多,对吧? 那么就可以假设个八六幺啊,那是你的机器是不是一千三啊?十三测数不太好算啊,对吧?不像前面几题那些都有很强的一个逻辑关系。像十八等于二十减二,十一等于十加一这种, 就是可以很巧妙的有他的一个运算技巧,像十三这个数就比没有什么特殊的一个技巧了。那一千三按六十二点一去增长,这点一 直接给他忽略掉,直接当成六十二来做就好了。因为两千乘以零点一个点就二啊,你选项差距有个二十多,所以直接当成六十二来做就好了。那是一千三,直接拆成一千加三百也很好算啊,对吧?一千乘以六十二不就是六百二, 那三百乘以六十二不就是一八六吗?对吧?那就加起来八零六,那一千三加上八零六是不是二幺零六啊?比二幺六幺是不是小了个五十五啊?那说明你的增量是不是要比八零六要大? a 选项排掉, 那你看这一回我们就不能说通过极限八零六加五十五不到小于八六幺来排除了,因为这时候还有 b 跟 c 啊。但是这里我们可以利用一个原则啊,只要挣扎率是小于一百的时候,这这个 他超过大部分都是机器的。大部分是什么意思啊?就是一半以上啊,五十五的一半以上都是机器的,那说明这五十五里面是这个增量,他的部分肯定是一半以下啊, 五十五的一半才二十多万,对吧?而且你再想一下,你刚刚这个八零六要到到这个八五三,是不是要加个四十多万?你看五十五要分个四十多给这增量,可能吗? 肯定不可能啊,所以是不是肯定就选 b 啊?你只要知道第二步这些这些叉子大部分都是机器的,小部分才是增量的,利用这个原则就可以把 c 给排掉了,那就选 b 了。 然后最后一题,这题更近一点, 而且数这么大,你看限期是四幺三七,增长率二十四点,一看选项七九七九九选项差距就四啊,更小了。那么同样的也可以结合选项来假设啊,那可以假设 多少啊?首先四千一减去八百左右,是不是还有三千三千三百多啊? 而且我们在假设的时候有个原则,就是尽量假设出来的机器要好算啊, 我们通过四千一减去八百左右,是不是肯定是三千三百多啊?那些三千三百多有个很特殊的一个分数啊, 三分之一是不是等于三十三点三三三三三啊,对吧?那我们是不是可以假设机器就是三三三三啊?那你假设的这个增量不就是八三四吗?减一下你的机器不就是三三三了吗?对吧? 那三三三按二十四点一去增长,那怎么算啊?左边不就是三分之一吗?那不就等于右边这个除三吗?除三等于多少?八零三啊,对吧?那你看 这两个相加多少?三三三三加上八零三是不是四幺三六?哎,离这个四幺三七是不是还差了个一啊?那说明增量要比四十零三要大,那 a 跟 b 是不是排了,就算一全加上去他都到不到 d 选项啊? 所以选息这个一的话,实际上基本上都是机器的,所以能能给的这增量的基本是没有的,所以答案就是八零以上,跟这个八零以上是一样的,所以这就是假设的准的话,基本上一步答案就出来了。然后第二步再结合一个极限,根据选项结合极限 就相当于你只算了一步,而且你第一步算的这个也是假设的,都是挺好算的一些数字就乘法有有很多速算技巧的,他们数字很多数字之间都有一个很巧妙的一个关系, 还是要就是做资料还是要分析为主,尽量少计算,如果你计算多了,那你动动脑的肯定少了,你哪道题目一上来就去动笔,所以你肯定不知道 数字之间还有各种各样的一个关系啊。
180拥抱昔日温度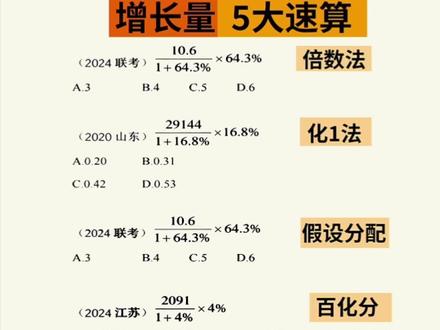 04:25查看AI文稿AI文稿
04:25查看AI文稿AI文稿今天给大家分享一下怎么样去快速计算增长量哈,物大速算方法,咱认真听一遍。先讲点倍数法哈,倍数法适用于限期量与 e 加 r 之间有明显倍数关系的时候去用哈。 选项差距还算还算大啊。那咱们十减六,直接看成十底下保留两位数值啊,保留幺六就可以了。那六十四除以十六,那是不是就相当于是四倍多一点的数值哈?答案得选四左右的个数,选 b 选项哈。 看一下化易法哈,化易法它适用于增长率小于百二十左右的时候去用哈。看一下这道题啊,我们知道增长量它其实就是限期除以一加上增长率再乘以增长率,是不是? 好,那左边这个式子,它是一个机器量,机器值啊,那么看一下这道式子的机器量是多少,机器值是多少?咱们分子分母同时保留有效数值三位数就可以,分子保留二九幺,分母是幺幺六八啊,保留三数幺幺七。好,这时候想办法让分母 约掉啊,幺幺七减掉十七就是变一百了,那就是可以直接忽略分母了哈。但是分母减掉一个数值,分子也得有变化,让分数保持不变了。减掉的十七,咱们可以看成减掉十一,再减掉六十一,他就是分母前两位的一倍哈,那分子也得减掉前两位的一倍,也就是减到二十九,好,那减掉六啊, 减掉了六六,是分母首位的六倍,那分子也得减掉首位的六倍啊,但是首位他都已经接近三了哈,咱们直接看三三六十八,减去个十八不到的一个数值。好,那这时候分母是不直接约掉了这道题,基期值长这样好,那二九幺是不依旧是限期?限期减掉这串数值是基期,那减掉的这个数值他不就是增量吗? 二九加上十八不到的一个数值,增量得选小于四十七,但接近四十七的一个数值,所以答案直接选择 c 选项哈。 再看一下第三种方法啊,叫假设分配,假设分配适用于增长率,他无法百化分的时候去用哈,看一下这道题啊,限期是十点六,十点六,我们要把它分成增量以及基期啊,这时候直接去带选项啊,增量三的时候十点六减掉三,基期就是七点六 啊,那三他都不到七点六的一半,但是人家增长了百六十多呢啊啊,这个 a 选项太小了,不能选啊。那再看一下 b 选项啊,增量为四的时候,十点六减掉四呢,就是六点六啊,六点六乘以百六十,那差不多是三点八多的一个数值接近四啊,这时候可以直接锁定 b 选项, 但不放心的同学,你可以去验证一下啊,看一下 c 选项啊,增量为五的时候,十点六减五,那机器量就是五点六,他都快接近百分百了,他都快增长百分百了哈,所以 c 选项又太大了, c 不 能选,只能选择 b 选项哈。 啊,看一下百分的方法啊,百分呢,适用于我们式子里面有熟悉的特殊分数的时候去用哈。你像这道题啊,百分四是不是可以看成二十五分之一啊?这时候用 n 加一原则的话, n 是 等于二十五啊,那二零九幺除以 n 加一,也就是二十五加一,要除以二十六 分子分母同时扩大四倍不到的一个数值,那分母不就消掉了吗?二四得八啊,选八十啊。再最后看一下这个误差,修正啊,选项需要精确计算的时候去用。 你像这道题啊, ab 选项实在相差太近了哈,那如果有些同学直接用百化分啊,这个百分七点六,你直接看成七点七啊,十三分之一直接去算啊,它会有误差啊,咱看一下,如果用十三分之一,它是一个负增长,所以要用 n 减一啊, 也就是幺二零六五啊,都有一个数值,不看除以十三减一,也就是要除以十二啊,那除出来一个数值,差不多是幺零零六的一个数值啊,它其实存在误差的。百分七点六跟七点七是不是还差百分一的一个数值? 好,咱估大了哈,那要减掉一个数值,减掉多少呢?百分之一,它的增量是在哪里?它是在基期量这边给他估大的哈。那咱们看一下,基期幺二零六五限期加上增量,增量直接用幺零零六代替哈,已经相差比较近了哈, 再乘以百分一啊,那就是幺三开头的数值要减去十三,幺零零六减去十三,是不是等于九九三九九左右的数值?这道题得选 b 选项哈,增长量用这五大速算方法去做,绝对是够用的哈,让你们计算更加事半功倍。 像这样的秒题口诀大概还有一百多个,是我们针对近五年真题整理总结出来的一些高频考点,一两个视频呢,肯定是讲不完的,所以把口诀给大家梳理整理成三天的精品技巧课。第一天讲数量资料啊,不用一个一个单独计算。第二天讲判退言语,二十秒左右去拆分题型,根据题型去带秒题思路。 第三天讲申论或者攻击踪影佩戴,还有思维导图啊,帮助大家梳理思路。另外还有我们自己内部的技巧库,整理好了五大板块,每个题型对应的口诀和真题啊,可以用来学习刷题和复习巩固。需要精品课口诀以及技巧库的同学我们评论见。
5707公考土豆学姐 05:33查看AI文稿AI文稿
05:33查看AI文稿AI文稿详细讲解一下假设分配法,有很多小伙伴让我们再仔细的讲两道题目,这个方法很多老师都有强调过, 假设分配法精确度确实很高,适合算一些选项差距小的题目。我们可以看到这道题目,这个是计算机算出来的选项,这个是假设分配法算出来的两个之间选项差距特别小,所以它是非常适合选项差距小的题目的。第二个特点是算法简单,我们可以看到我们只能把它拆成一些简单的加减法, 乘法就可以算出一个近七厘米的增长量,可以说我们的时间少了一半,算法难度也少了一半。好,那下面详细的来讲解一下这个我们是到底是怎么算的操作流程呢?就是这四步,我会结合立体讲解来讲一下这个流程。看到这道题目二百二十六除以一加百分之四。 第一步是取整式态,就是我们要取一个整百,至少是整五或整十的数,就是从二百二十六这个数里面取,把它分成一个整百和一个和剩下的数。那我们先写分成这个整百数,我们二百二十六取的整百就是两百,这是一步取整式态之后呢?第二步计算增量, 这个时候增量是什么呀?是我们这个时候的增量,是我们这个时候的总百,两百去乘上我们的增量,就是这个增量,把它写到这边把。 然后呢我们要做的第三步剩余分配,剩余分配就是把我们原来的数减去两个分配的数,剩余的量就是这个十八,也就是二百二十六减两百,减八等于十八,这个是剩余的数,剩余的数呢?同样的,我们还是像一个叠代一样,如果剩下的十八是比较大的数, 大的数的意思是他可能对于选项来说,音阶可能会比较大的数,那我们就再一次迭代回去,到这一步,剩余数再取整数。刚刚说了,我们取一个乘五或者整十的数,那就取一个十五。第二步是什么?第二步计算增量,乘过来 十五乘以百分之四,就是零点六,那剩下的这一步就是剩下的就是十八减十五,减零点六,又是剩一点,剩一点,那这个二点四呢?它这个数已经比较小了,我们直接处理调这个误差,也就是把剩余的数归于机器内,所以我们的机器就是这三个数相加 二百一十七点四,增长量呢?就是这样的数相加等于八点六,跟计算机算准是不是很接近?好,我们大概了解了这个操作流程,再做一道题啊,这道题呢,它的特点是增长率很小,数, 也就是计算的会更加复杂一点。我们来看一下取整或者不取整的误差有多小呢?我们来做一个验证。第一个 先不取中,还是一百分之六十点八来计算。对,我们这个假设分配法,第一步是什么?第一步先取中,试探二百六十八,我们取中第一步,取中的话也是同样取二百。第二步是什么?第二步计算增量,增量是什么?就是二百乘上百分之四点八, 得到的是九点六,二百六十八,减去分配掉在这两个数,剩余的就是五十八点四,那我们将呢剩余分配五十八点四,这个数 挺大的,所以我们要再叠带回去来一个。同样的是取整,试探五十八点四,取整最后取的是什么?当然是五十。第二步是什么?第二步是计算增量,五十乘以四点八等于二点四,那剩余的量是多少? 就是五十八点四减五十减二点四乘以六到六。这一步呢,我们其实还可以再分一下,还可以取整,取一个五,再取一个零点二四,剩余的就是零点 六减五减四零点七六,我们就可以得到左边的这一堆和剩下的这个余数记清,等于二百加五十,加五加七点六,就等于二百五十五点七六。 考试的时候如果选项差距没有那么小的话,我们到这一步六就可以直接误差处理了。计算器算出来的这个除数等于二百五十五点 七二,那么我们可以看到假设分配法和计算机算出来的几率相差特别小,那我们再来看第二种方法,因为百分之四点八,我们算这些乘啊减的时候都挺麻烦的,那我们就试一下给他约等于百分之五的时候,会是一种什么情况? 那同样的,首先二百乘百分之五,这个是十,剩余五十三。同样的,我们还是这样,除以五十 五是乘以百分之五,那这个时候差就是二点五,余下的是五点五。同样的,我们如果想再假设分配一次,就是五乘以零点二五,余下的是零点二五, 那我们接起同样是左边的两百加五十加五加零点二五,等于二百五十五点二五,这两个数比起来差距其实也挺小的, 误差是可以接受的,我们考试的时候,如果增长率是一个小数,我们也可以考虑将它化成一个整数来用假设论倍法计算,这是针对于算七七,我们可以 取一个,我们可以化小数约为整数,那我们对比一下这个增长量,九点六加二点四,加零点二四,这样加一下等于十二点二四,那这里呢?等于十二点七五, 实际的增长量等于十二点二八,我们可以看到原增长率计算出来的增长量,十二点二四,十二点二八是非常接近的,但是呢,一旦取了 总数的增长量的,那相差来说还是有这个大概百分之零点五的这个误差,因为你看这个点它就是零点五 三百十二,就百分之零一五多的误差吗?这个时候呢,我们如果是计算等整面的题目,如果它选项差距是在小数,最好是用圆来的增长率计算。好,我们上期讲解完了,大家要做题目,也可以试着用这种方法哦。
148上岸独角兽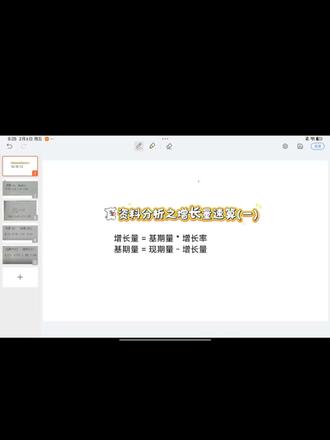 05:59查看AI文稿AI文稿
05:59查看AI文稿AI文稿今天来给大家分享一个增长量的速算技巧,来直接看题目,其实当遇到这种题目的时候,特别是看到这种选项, 很在考场上很容易纠结,也容易慌。其实咱们反过来想一下,给的这几个选项是不是有一个正确答案?而咱们如果用这个选项的话,是不是就在告诉咱们, 如果这些选项差距比较小的话,是不是越就告诉咱们更接近答案?所以这就牵扯到今天所说的一个假设法, 直接来看原理上面所说了,增长量等于机器量乘以增长率,而机器量等于现期量和减去增长量,这是两个最简单的公式。如果咱们现在假设 增长量, 然后再用限期量减去假设增量,增长量是不是假设机器量, 而咱把这个假设机器乘以这里的增长率,是不是又反过来等于这个增长量?所以当咱们假设增长量 和增长量很接近的时候,这个就是就是答案。咱们直接来拿题目演示一下吧, 比如这个题,其实这个题看了之后有一个很快速的方法, 为十百分之十四点五接接近百分之十四点三,就可以看成七一八,对吧?用一二六四除以八就这样。但是我这想说的是假设法, 这直接来看题目,我这会假设一六四,这是为什么呢?因为选项就告诉咱们这里面有一个其中答案,而他这个答案在一百二到一百八之间, 我为什么会假设一百六十四呢?一是他一千二百六十四减去咱们假设增量是不是等于一千一百, 这样就方便咱们计算,而且他在这个范围之内,所以咱们这样再继续一千一百乘以百分之十四点五,是不是一千 一千五百一百五十九点五和一百六十四很接近,所以这个题就可以选 c。 下面咱们继续看这个题,这题用刚才所说的那个,如果是它看成百分之十一点一, 看成九一十,这题就就错误了,这样算出来的话是一六九九,除以个十是一百六十九,可能大部分都会选 b 了。其实这种是错误的, 并不是说方法错误,只是说放在这种差距悬差距小的地方不是不太适用。咱们来这时候同样来看这个题目,直接假设 一百六十九,为什么呢?他是不是在这中间?而且他这个限期量是一千六百九十九,减去一六九是一个比较容易算的数, 这个数算完之后是一百,是一千五百三十,这时候再乘一个一一一三,就可以算出来是一七二, 所以这是一个,这样就算一个乘法就会很快,所以这时候是不是他在咱算出来的更接近一七二,所以这样他在一六九和一七二之间 一七二点多,然后所以这个就选 c, 继续来看一个看一个 d 这个题吧,其实这时候大家可以做一下,把答案打在评论区都可以。其实我先给大家直接演示一下吧,就是咱们不是因为有这几个选项吗? 你可以直接假设为四百七十五点五,咱们纯属是为了方便计算。其实到时候之后熟练了这个四百七十五点五完全可以不用写,直接你知道它属于这个,直接你直接用六千乘以百分之八点一,是不是 四百八十六?四百八十六的话他在四百七十五和四百八十六之间,这这样你就需要稍微调整一下他是不是百分之八点一, 他俩的差距是十左右,如果他这面上升时,这边是不是下降零点啊?所以这题就会选 c。
125world








