origin怎么做一元线性回归

如何用 origin 做线性礼盒？一般我们做礼盒会在 spss 或者 excel 中操作，其实用 origin 也是比较容易操作的，在做完图之后，直接在 origin 中礼盒是非常方便的，给大家操作演示一下，做线性礼盒需要用到点图，我们先选中数据，绘制一个点图， 点击分析拟合。线性拟合打开对话框，打开之后会显示线性拟合的弹窗，点击输出量模块，这里面有很多选项， 一般我们做回归分析的时候要添加置信区间，做相关性分析的时候是不需要置信区间的，选择需要的拟合统计量和拟合汇总后点击确定， 这就是拟核之后的结果。我们可以看到刚才勾选了哪些输出量，它就会输出哪些数据，对于不需要的数据也可以进行删减，选中不需要的 数据后点击叉号即可。做完图之后，在原始表格中会有一个详细的报告，报告里面会显示二平方 p 值等数据， p 值是显著性相关系数，就是你的相关性显不显著， 一般批值小于零点零五，我们认为它是显著相关的，这个 p 二三三二是相关性系数，这个值大于零点七的时候是强相关，零点五到零点七是中等相关，零点三到零点五就是弱相关。

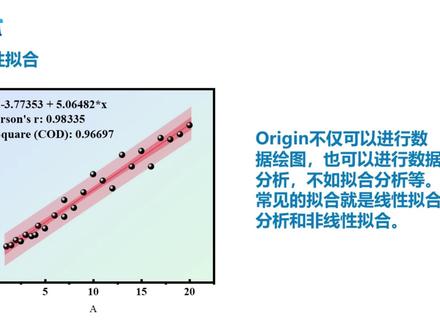
如何快速绘制这种线性回归图？导入数据，然后点击右边的 rap maker， 将 s 和 y 列数据拖入到弹窗中，其他地方可以不用管。然后勾选上你和 点击礼盒，将方程和 r 方勾显示在将致信区间和预测区间勾选上，点击确定，这样就做好了。

朋友们好，本个视频我们来讲解一元线性回归模型及其应用。 其实整个概率这一块，很多同学会感觉他比较抽象，我们就简单直接来说，在上一个视频当中，我们知道就是在统计学当中，我们会经常涉及到统计出来很多数据，比如以我们上节上个视频举的这个例子， 子女的身高和父亲身高的比值比例关系，或者是他们之间的一个相关性啊相关性，我们得到这么一样一些散点图意外线性回归模型呢？就是我怎么样找到这么一条最优的直线 来估测这个子女和父亲身高之间的这种关系，那也就是说这条直线呢，我们把它写出来肯定是一个直 直线方程，就是这种形式， y 等于 bx 加 a 加 e 这种形式，它就是 y 关于 x 的一个线性回归模型。结合到这个例子当中，也就是子女的身高和父亲身高之间的一个估算的一个关系， 其中 y 呢称为音变量， x 称为自变量，也就是说我先有已知父母的身高身高，我由这个模型来预测一下，或者说估算一下子女的身高就可以了。 所以的话，现在呢，那关键的问题就是我们怎么样找到这么一条直线，使得这一条直线模拟这些散点图的这个效果是最优的， 是最优的。那么这个直线方程呢，我们是结合最小二乘法来得到的，来得到的这个公式，这个 课件当中没有写全啊，我在这个位置再给他写一下，这个呢，我们就将外间等于 b 间乘以 x 加 a 间称作外。关于 x 的一个经验回归方程，也就是我们由内一些 一堆三点图，一堆数据，然后得到这么一个方程，来估算父亲和孩子身高之间的一个关系。这个方程呢，我们称为经验回归直线，或者说经验回归方程啊。 那么这里面的这个 b 间和 a 间是怎么得到的啊？我们通过我们得到的一大堆的这些数据，就是 x 一一直到 xn 这一堆数据。 b 间呢，就等于上面是一个求和公式， i 从一到 n， 对谁求和呢？对 x i 减去 x 杠， 乘一个 y， i 减去 y 杠，然后除一个。下面也是求和，爱从一到 n， 对谁求和呢？对 x， i 减去 x 杠，括号的平方求和。 在这个公式里面啊，我们解释一下 c 个码，爱从一到 n 就是对他们进行求和，也就是我 x 一带进去， y 一带进去， x 二带进去， y 二带进去，每得到这这些数，对他们求和。这个 x 杠呢， x 杠就是 x 一到 x n 的均值， 也就是平均数，外杠呢，就是外一到外 n 的均值也是平均数。由这个呢，我们就得到了这个 b 间，这个 b 间。另外呢， b 间还有一个常用的公式，我给他写到下面啊，要下面可以用它啊，也就是 c 个嘛， i 从一到 n， x i， y i 减去 n 倍的 x 杠成一个 y 杠， 除一个 c 个码， i 从求和， i 从一到 n， x i 的平方减去 n 倍的 x 杠的平方，用它也可以更多的，我们 更多的时候是用这个公式啊，就直接把 x， i， y， i 分别带进去求和，后面呢， x 杠， y 杠就是他们的均值，算出来，直接带入运算就行了， 这个我们就得到了 b 间。 b 间呢？ a 间呢？ a 间就比较简单了， a 间直接就是由 y 的平均数减去 b 间，成一个 x 的平均数就可以了，就 ok 了。然后呢，我们由我们得到的从一到 n 这一组，这一对，这一堆数据当中，我们算出来 b 间， 算出来 a 键。好，所以回归方程得到了，就是它，我们就可以拿这个方程，然后来估算。比如再给我们一个父亲的身高，让你估算孩子的身高，那我就可以用这个模型来估算了，就是这个意思。好，那下面我们思考两个小问题，第一个 经验，回归方程一定过他的这些点当中的某一个点吗？我们看一下这个方程， b 间、 a 间，这个可不一定啊，记得，这个不一定啊， 不一定啊，不一定的。就像我们上面画的这个图，这一条直线虽然是你和效果最优的，但是他一定过其中当中的某一个点吗？ 不一定，极端的一种情况，比如我们得到的这样一些数据，很对称很对称的两端，那这个直线肯 肯定是在他俩中间的位置啊，不一定过某一个点啊，不一定过某一个点。然后看第二个小问题， x 杠 y 杠，也就是 x 均值， y 均值在经验回归线上吗？这个是在的啊，这个是在的，因为我们这个 b 间、 a 间都是由这个 y， 你看看这个就是由他得到的，所以我们把 x 杠外杠均值带进去之后啊，带进去之后他肯定是成立的啊，他肯定是成立的。好，这个就是关于这个一元线性，呃，一元线性回归模型， 一元线性回归模型它的定义以及它的长这个公式啊公式。

大家好，这节我们介绍的是一元线性回归，一元线性回归他指的是自变量只有一个的情况下，那对应的多元线性回归就是指自变量有多个的情况下。 因变量不论何时我们在进行一次检验的时候只能有一个，所以这个就不做强调。那么上一期做相关的时候，我们也说了，相关是第一步 回归是定因果关系，同样适用的都是两列连续数据变量，那么接下来我们来看具体的操作。点击回归线性，我们以身心 准备为字变量，生活准备为音变量，这样的话我们就选好了变量。当然实际情况我们根据自己的 变量情况，我们考虑了哪些因素，就把它作为自变量，考虑了哪些被影响的指标，就把它作为音变量。因为我们这些准备情况，它基本上都是属于同一个部分， 就说本质上他们是一个总体的不同部分，那么他们既然是一家子，肯定就不用定因果，只是我们从数据类型上给大家举个例子，所以大家在实际中需要注意一下，就是 比如说我们要调查健康状况，那健康状况这个总的两表他划分成了四个部分，这四个部分本质上都是属于健康 状况这个总体，所以他们内部就没有需要定因果了，大家都是一体的，同进同退，不存在因果的问题。选择好了变量，那么我们就点击确定， 这样的话就得到了一元线性回归的结果。这个表格是关于变量的介绍。一般情况下我们的实际用的，生活实际用的时候，就不管第一个模型摘要，模型摘要这个是模型的数量，是第一个，这个也不用管。阿尔方他叫负相关系数， 指的是自变量和音变量的相关程度， 他指的不是直接数字上的相关程度，嗯，指的是背后从统计学原理上，嗯，他的意 些变异，当然涉及到一些分布呀，和变差的，变差的分解呀，这些我们就不用管，只知道他是负相关系数就行了。 r 方代表了自变量，能够解释因变量的 比重。假如说因变量我们的信息量是百分之百，因变量能够解释它的百分之六十三点五，那么这个 r 方就是六十三点五，它有一个校正公式，在 线性回归，一元线性回归里面，我们用 r 方就行了。如果是多个字变量，那么我们一 一般要用调整后的 r 方，这个标准估算的错误，这个我们也不用管，不用，因为他是从公式上来说是一个关键的指标，需要把它放上，但是我们在实际中用的时候，嗯，基本不分析，也不管，所以就不用他。 总的来说这一块有用的就是这个指，或者说这个指具体看自变量的情况，也就代表了 r 方，自变量能够解释音变量的百分之六十三点五的变化量，这个他看他有没有用是有前提的。就是当回归模型显著的情况下， 那么我们就来看回归模型 f 值是这个显著性，是这个显著性小于零点零五，说明 在整个模型中字变量对音变量有显著影响。因为我们这是一元线性回归，只有一个字变量，所以这块的结果和这块的结果是一致的，因为只要这个变量字变量显著了，那这个整个回归模型就是显著的。 如果是多个自变量，那这块只能说明所有的自变量至少有一个对因变量有显著影响。那回头我们再多重线性回归里面那里来说， 现在我们从这里能够判定这个回归方程模型是显著的。回归方程模型显著，那么这个值他才是有意义的。如果说回归模型不显著，那么不管这个值是多少，都属于误差。当然在我们这个数 里面他是有效的。整个回归模型是这样有显著，具体的影响程度是这个他其实也叫拟和度， 就是这个回归模型和具体数值的匹配程度。我们有假如说我们调查了一堆数据，然后我们建立出来的这个公式，这个公式和这一堆数据的匹配程度就是这个值，其实就是字变量对应变量的影响程度。 那我们再来看回归系数，回归系数就是要具体化，我们通过这个具体的数值给另一个自变量可以算出音变量身心准备，他的回归系数是零点七四零， 这是他的显著性检验，用的是期检验，显著性小于零点零五，身心准备是显著的。从这里我们可以得出来一个回归方程，就是 生活准备等于零点七四乘以身心准备，加上一点零二五，一点二零八， 这样我们就建立起来一个二元一次方程给定一个值，那么这个根据既定的算，呃，既定的数值就能够算出来另一个值， 我们一会会把它呈现在最终的书面形式里，这整个就是关于一元 线性回归方程的解释，那么一元线性回归方程我们就到这里了，接下来给大家看一下整理出来的书面形式。 那这就是最终的呈现形式，回归系数部分常亮它的系数显著性，身心准备回归系数显著性模型的 r 方 f， 整个回归模型的显著通显著检验的指标值 f 值，这是 f 值对应的显著性， 这是关于文字解释回归模型显著字变量对因变量有显著影响。模型而方的含义在回归系数检验 中，身心准备对生活准备有显著影响。回归方程，哎，这块写错了，不好意思， 这就是回归方程。如果把这个身心准备换成我们的 x， 生活准备换成 y， 这就是我们以前学过的方程吗？只不过以前人家的方程我们在学的时候是给定的，现在是我们自己的数据算出来的。假如说身心准备等于一， 那生活准备就等于零点七四乘以一加一点二零八，算出来对应的数值。 如果说身心准备等于二，那零点七四乘以二加一点二零八，就等于生活准备，这个是给另一个数值，我们就可以计算出来， 这也是回归模型的预测作用的意义。当然一般情况下我们不用，一般情况下我们只需要证明字变量对应变量有显著影响就行了。这个就是关于一元一元线性回归全部的结果。那么今天我们就到这里啦，拜拜。