奈奎斯特图求传递函数

好的， 各位同学，我们这节课呢，给大家讲一个小小的一个技巧啊，这个技巧其实很简单，也就这两个图，也就说是两个门函数距离的结果， 为什么一个很简单的一个结果，我要在这里给大家主动强调呢？那么首先大家还是从结论本身入手，大家看一下啊， f 一和 f 二是两个门函数，那么这两个门函数卷积，哎，卷积完之后就会成为我们的一个什么一个三角脉章函数， 但是呢，这是有个前提的，你一定要注意，你看这个门框，比如说只有两个等宽的门函数，他卷积完之后才是一个三角脉冲，那么并且从这个三角脉冲这个地方，大家需要注意几个点哈，一个就是你这个卷积完之后的这样的一个 宽度，他为原本两个门函数宽度之和，哎，你看原本一本，一个是二分之套，一个是二分之套，卷进完之后是套吗？对不对？另一个呢，就是你这个高度， 高度，大家会发现你这个高度其实是一个，是吧？其实是一个函数面积乘上另外一个函数的符值，你说是他的面积乘上他的符值也好，还是说是他的 面积乘上他的肤质也好，那其实是一回事，对吧？因为你看，不管是他跟他乘还是他跟他乘，那不都是一样的吗？对不对？好，这个就是两个等宽的一个麦函数， 那么放在一般情况下，两个不等宽的满数，那其实出来的结果是一模一样。你看哈，首先两个不等宽，一个门宽是二分之套一，一个门宽是二分之套二，那你会发现他卷积完之后的门宽是多少？是二分之套一加套二吧，这第一个点，第二个点呢，就是我们因为两个卷积完之后，他 这个等腰体型吗？等腰体型，那你这个点的位置就是二分之套一减去套二，对吧？那现在这两个点大家都记住之后呢？你会发现，当两个门框 等宽的时候就套一等于套二的时候，你是不是这个地方为零，为零是不是就变成等腰体型了，对不对？好，这就是两个啊，两个我们的一个点， 然后另外一个呢，就是我们的一个浮子，那你看到的浮子等于一，一乘上套一，乘上个一啊，那么我们这个浮子其实怎么取的呢？一般来说我们取门宽比较窄的那个矩形的面积，你看这两个的话，哎，你这个套一明显是比套二要窄的吧，那所以说是一一套一，就是比较窄的这个门的一个面积 呈上，哎，你这个比较宽的门的扶持，那么就作为你卷漆后的这样的一个幅度值，所以说这一些简单的一些技巧哈，大家是一定要记住。并且对于 这几个点就是我给大家圈子的这几个点，你要知道，你要能够快速的给他写出来，知道吧？这个是我们今天给大家讲的这个支点，那么这个支点为什么要单独给大家拉出来讲一下呢？ 其实这个门函数啊，他在我们后面是有非常多的一个用武之地，一方面是我们函数的一个本身，哎，另一方面呢，大家知道吗？你们的其实学的一个上函数，他跟你这个门函数，他其实他们之间是一个副列变换，对的，你的上函数，你到后面你也会发现你用的是蛮多的，确实蛮多的， 很多时候你在食欲分析不过来，你可以把它转化成频率去进行一个分析，那么同理，如果说你的食欲是这个 gt， 你也可以把它转化成，哎，转化成这种， 这种，这种，这种频率用四上函数的形式给他进行分析，因为所以说这两个就是这两个信号是大家在后面是经常遇到的，并且他我们是经常用，会用在什么频率 欲和食欲这样的一个转化呀？或怎么样？所以说这个门还出了个卷机哈，这块大家还是需要呃给他了解的，这第一个，第二个，那就是我们比如说哈，你放在耐克斯特那里面看，耐克斯特那呢？我们都知道你的一个信号要想满足吗？无私人会不会讨厌你的一个重要型号 fs 必须大于等于二倍的 fm， 对不对？这这个这个定理器大家都知道，那么如果说两个信号哎，我们在食欲上有一定的运算，那么他的一个瓶带宽度一个是一个怎么样的变化呢？ 对不对？那么这这个这个其实啊，大家应该也都知道哈，如果说假设 f 一的平带宽度是欧美改一， f 二的平带宽度是欧美改二，那么我现在我们在实际上一般有几个预算，第一个 f 一加 f， 那么 f 一加 f 二之后在频率里面是不是就是 f 一也是加 f 二的？那么最终他们加完之后，你的一个贷款是不是应该等于的是 欧美感一和欧美感二中的一个最大值吧？这个大家应该好理解吧，你看假设这个是欧美感一， 这个是 omega， 那你两个加完之后，你肯定你加完之后的一个新信号，你的贷款肯定是一个最大值啊，这样的话，你看是不是就可以得到这个两个信号相加完之后，你 星信号他的一个带宽的最大值就可以得到，那他星信号带宽最大值，那你是不是可以得到星信号的一个耐克斯特彩阳定律了？这一个 f 一加一法，那么如果说 f 一乘上个 f 二呢？那么大家根据我们的决定就知道食欲乘积等于什么频率， 卷基？平玉卷基，那平玉卷基，你知道我们该又该怎么求？那其实像这种的话，大家怎么会说呢？你可以在脑海中就把这两个门函数给他，记得你看你比如说哈，你这是一个平玉 是 f 一，这个是 f 二，他们那个频率这样子，反正你因为你只是想要利用这个带宽嘛，两个卷进完之后，你看他新的带宽变成什么条件嘛？那我们就举个特殊的案例喽，假设 f 一是这样子， f 二是这样子，那么两个卷进完之后，你看他们卷进完之后是不是一个等腰体型 等，要提醒你，这是他的一个最大的一个，一个一个最高频，那就或者最高频他等于什么？是不是等于哦买噶一加哦买噶， 那你这个欧美港是不是变成了欧美港一加欧美港二？好了，星星号的最高频友找到了，你是不是又可以求助他的一个欧美港 s 或者说 fs nex 的产量定律了，对不对？那么再者你 f 一卷积上 f 二，你对应的频率是什么？是 f 一乘上 f， 那你看这两个相乘，它的一个新的 omega 是不是等于什么？等于的应该是 minimalomega 一 omega 啊，你这个好，又找到了，又找到之后你是不是又可以得到一个新的 omega s fs 了？是不是？所以说你这两个门函数的卷机，他出来的这个波形啊？这个大家一定就是你要作为一个潜意识，或者说作为一些就类似于非常基础的一个知识，你要能够给他掌握，这样的话对于大家后面在做题的时候是非常非常有帮助的，知道吧？好，那这是我们给大家讲的这个知识点。

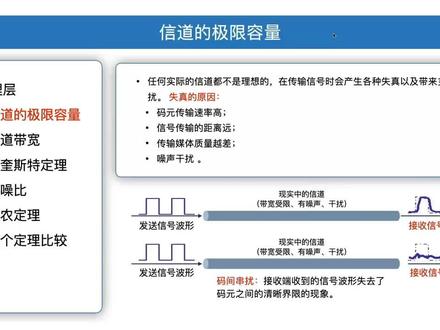
各位观众大家好，欢迎观看计算机网络视频课程，本次课程我们将学习信道的极限容量， 课堂的内容呢包括以下几方面。第一个呢，什么叫信道的带宽，然后我们介绍一下耐奎斯特定理，信照比的概念以及相融定理。最后我们给一个例子来对两个定理进行一些比较。 在学习信道的极限容量之前呢，我们先来了解一下什么是马原， 什么是马源呢？马源就是在时间域上某种波形表示数字信号的时候，它代表不同的 离散素质的一个基本波形。前面我们那种调制的方法讲了两种，一种呢，改变某一种属性代表一个比特，是一种波形，有政府是一种波形，没有政府又是一种波形。 我们前面又学了同时改变那个波的两个属性，一个正符，一个向尾角，那么这个时候这个基本波形就能表示四个比特了。 所以有前面那个例子之后呢，大家就知道一个马云可以携带多个比特的信息量，这个马云就是某种波形。 举一个例子，我们来看待这样一个问题，比如说出租车，如果你坐一个人的话，我们可以认为这个出租车呢可以表示一个比特，如果他坐两个人呢， 我们认为这个出租车可以表示两个比特。当然我们可以用出租车不同的颜色来区分， 前面说的呢是这种模拟信号。当然我们的方波也可以有多种状态，比如说当马源的离散状态有 m 个 m 大于二时，我们这个马源叫做 m 进制的马源，这是在方波的情况下，我们来看 我们看下面这个例子，什么叫二进制马原呢？电压是一，表示一，电压是负一呢，表示零两种状态。很容易理解，二进制马原，那一个马原一种波形， 这是一种波形，这是一种波形，只能表示一个比特了。什么叫四进制马原呢？就是我把它电压范围呢， 定了零一二三一共四种状态，电压为零呢，我表示零零的组合，四种状态吗？二进至两位就可以把它编完，所以呢，电压为零，我可以定义成零零。 电压为一呢，我把它定义成二，定制的零幺。电压为二呢，我可以定义成二，定制的幺零。电压为三呢，我定义成幺幺。所以 传输的不同的电压就表示了不同的比特的组合，因此这个马元呢，它代表的比特数就比这种马元代表的比特数翻倍了。原来你只能表示一个比特，现在呢，我表示了两个比特， 下面我们再看一下八禁止马元，那我电压呢，从零到七 进行变化，并且给他做一个定义，零呢，表示零零零零七级八种状态，三位二进制就可以把它编完，从零零零零到幺幺幺幺，那么对应的和我们这种四进制马元是一样的，我们把 电压为零，表示二进制的三个零。电压为一呢，表示二进制的零零幺。电压为二呢，表示二进制的零幺零。电压为三呢，表明是二进制的零幺幺， 所以我们用这种方式可以让这样一种波形呢，表示的比特数就变成三个比特了。当然你还可以有十六竞争的马源，每一个这个马源可以表示四个比特了，这就是我们马源的概念， 那我们这样想哦，如果我们发送马云的速率越快，是不是我们的比特速率也就越快了？ 比如说我们的出租车，每次假设装一个人，我每秒发送十辆，那就是每秒十个比特出去了。如果每辆出租车每个里面坐四个人，那么每秒十辆的话，就每秒四十比特出去了。 所以大家知道比特速率其实和马原速率是有关系的。 这里我们就给出一个四进制马云的一个例子，比如说我要告诉对方八位二进制串零零零零幺幺零幺幺，假设我用拳头， 这个拳头就是一种马元了，表示零，手掌也是一种马元，我来表示一，那么这个时候一个马元只是表示一个比特了，我要传输上述二斤值未串的话，需要八次手势，你要发送八个马元。 现在假设我们规定用这种手势代表零零，用这种手势代表零幺，用这种手势代表幺零，用这种手势代表幺幺的话，那我同样的传输这八位二进之踹，我只需要四个手势就够了， 因为我每一个马元就发送了两个比特，我只需要发送四个马元就可以了。下面我们就来分析什么是信道的极限 容量。首先我们来看看什么叫做信道的容量，我们这里讲的信道的容量，就是我们开始介绍物理层上的时候，我们关心的问题之一就是我的消息最后变成计算机的数据，数据呢要变成信号在信道里面跑， 那么我这个比特变成信号在信道里面跑之后，我关心的就是这个信道，他每表中能够传输多少个比特， 我们希望你这个信道传输的比特越快越好，这是每秒能够发送的比特数，越快越好，这就是所谓的信道的容量。当然信道里面跑的是信号，信号呢可以代表一些比特，所以我们一个信道他的极限容量是多少呢？ 这是我们本次课程要探讨的内容。前面课程我们学了一个马源的概念， 所谓马原就是某种波形，他能够表示一些比特的组合。前面我们学了如果这个马原采用调频漂浮调向改变郑宣波的某一个属性的时候，这个马原呢只能表示一个比特， 比如说正幅为零表示零，有正幅表示比特一，这个时候这个波形只能表示一个比特， 那我们还学了 q a m， 我们同时改变这个波形的正符和向位角，那么这个时候我们这个马云他就可以表示四个比特的一个组合了， 所以我们的马元素率越高，也就意味着比特素率也就越高。那我们的马元素率能不能无限提高呢？那事实上是不行的，因为我们现实生活中的信道， 它是带宽受限，并且有噪声和有干扰的，在信道里的满员在这种信道里面去传输的时候，会出现积变、脱尾还有展宽的这种现象， 在接收端呢，就有可能接收到一种失真的这种波，我们把这个呢叫做马尖串绕。 那么马云的传输速率越高，大家马上可以想象马建川扰呢就越严重，因为 本身你这个马元在传输过程中变宽了，然后还有这种脱尾的现象，那么你马元素率越高，意味着单位时间内的马元的个数也就越多，马元一个一个的挤在一堆，这个时候我们就没有办法清晰地标明每一个马元的边界了。 那么失真还有一些原因就是因为你的传输距离太远了，信号衰减，还有本身你的传输媒体质量非常差。另外一个很重要的原因就是由噪声的干扰，因此我们心道里的马元素率不可能无限提高的。 这里我们简单给出一个马尖穿袄的例子，这个例子可能不是很恰当，但是也能说明一个问题， 比如说站在一个马路边上，想数一数单位时间内通过的汽车的数量，如果单位时间内出现的汽车的速度太多，而且太快，那么这个时候我们实际上是无法识别的， 那这个时候我们就根本数不清楚有多少辆车从我们面前过去了。假设每一辆汽车是一个马云的话，速度非常快，一辆接一辆，单位时间内通过的汽车太多，没有办法计数， 那慢一点的呢？我们就可以计数了，我可以很方便的识别一辆一辆的不同的汽车。 什么是信道的带宽呢？信道的带宽就是指你这个信道能够通过的信号的一个 频率范围，定义为这个信道里面能通过的信号的最高频率和最低频率之差，这就叫做信道的带宽。 那我们看一下电话线的线道带宽，他容许通过的最高的信号的频率是三三零零赫兹，最低呢是三百赫兹，所以他俩之差呢是三千赫兹， 那低于三百赫兹的信号，在这个电话线这种信道上是不能够通过的，高于三千三的，比如说这四千赫兹的这种信号，在这个信道里面也不能通过。所谓信号的频率， 这个大家都知道，单位时间内他重复的次数越多的话，频率就越高，所以我们这里讲的带宽是指的姓道的固有的一个物理属性， 指的是允许通过的信号的频率范围。我们在计算机网络里面，大家经常说贷款的概念，你的网络接入贷款是多少啊？那个贷款的意思指每秒比特，所以两者是有本质的区别的。 那姓道的带宽越宽呢？意味着他的高频分量越多，也就意味着他这一部分就越高，数值就越大，那么也就意味着我们可以用更高的数率去传输马源，而不会出现马尖踹 串绕。当然马元素率肯定是有上限的，如果超过了这个上限，就会出现马尖串绕。 一九二四年的时候，耐奎斯特就推出了著名的一个耐视准则，这个耐视准则是怎么定义的呢？ 在理想低通条件下，为了避免马尖串扰，马原的传输速率的上限值是什么呢？是两倍的 w， 我们单位叫波特，这个 w 呢就是信道的带宽，就是你这个信道允许通过信号的最高频率和最低频率之差，单位是赫兹。 耐试准则仅仅是给出了马原的在心道里传输的一个极限速率， 他并没有给出你这个信道里面的比特极限传输速率，但事实上两者是有关系的，因为我们说马原就是表示了一些比特的组合， 马源速率越高，比特速率也就越高了。我们要提高比特传输速率，我们可以采用这种编码的方式，例如我们这种多元调制的方法，让每个马源呢携带更多的比特。这个在前面课程已经讲过了， 比如说我们前面讲过的二进制马源，那一个马源呢，可以表示一个比特，四 四禁制马云，一个马云呢，可以表示两个比特，八禁制马云呢？一个马云可以表示三个比特，十六禁制马云呢？一个马云可以表示四个比特， 所以我们可以让马云能够表示更多的比特，就能提高他的比特传输速率。因此理想低通条件下，他的极限比特速率是多少呢？ 就是二倍的 w 乘以 log 以二为底的 v， 这个 v 呢，就是你是多少定制的，比如说二定制的，那么就是每个马云表示一个比特，如果是四定制的， 每个马云可以表示两个比特，等等。我们用一个例子来说 说明耐奎斯特准则，在无噪声的情况下，如果你的某个通讯链录的带宽为四 k 赫兹，采用四个相位，每个相位具有四种政府的 q a m 调制技术， 那不就是十六种状态吗？就是我们前面讲过的那十六个点，他让你求这个通信链路的最大数据传输率，指的就是每秒比特， 那这种信号就有十六种变化呀，因为你有四个相位角，有四种政府嘛，所以它是十六种变化。那我们用奈时准则去算一下， 用这个公式把它带进去，你是十六定制的，所以这是十六，那最后算得就是每秒三十二 kb。