已知sn求an通项公式
来看一道高二必考题,已知 a n 和 s n 关系是求树立的通向公式。观察唯一已知的柿子,发现柿子当中既有 a 又有 s, 相当于一个方程两个位置数,所以肯定不能单独通过这个式子求解。既然是求 a n, 我们的一般思路是把式子当中的 s 想办法变成 a, 这样式子当中就只有 a 就有办法了。因为 a n 一定等于前 n 项和减去前 n 减一项的和, 我们就是用这个式子来做这种题。既然要用 sn 减 sn 减一,显然原体已知的式子当中没有 sn 减一,那么我们就令 n 等于 n 减一,此时式子变成了 sn 减一等于二分之三, an 减一,再减三。显然用第一个式子减第二个式子,得到这个样子, 整理一下,变成 an 等于三倍的 an 减一。这很明显是在说 an 是一个以三为功比的等比数列。但是要 要注意,我们开始时令 n 等于 n 减一,写出的 sn 减一,而数列的下标必须是阵阵数,所以 n 减一必须大于等于一,也就是 n 大于等于二。要想写出这个等比数列的通向公式,还得知道 a 一用原体给的式子令 n 等于一,就能算出 a 一等于六。那么就得到了最终答案,你学会了吗?
粉丝3.4万获赞36.9万
相关视频
 03:00查看AI文稿AI文稿
03:00查看AI文稿AI文稿同学们,你们知道学霸是如何秒杀这种题吗? and 方前面的系数是一,所以 d 等于二,然后按一等于 s e 等于一,加二等于三,所以直接可以去求通向公式。 不到五秒钟把这道题做完,接下来给大家讲一下这么做的原理是什么。首先我们知道等差数列的前项和等于 化解一下, 所以大家以后记住,在等差数列当中, 如果 n 是一个等差数列,那么 s n 等于二分之 d 倍的 n 方加上 b n 前面这一堆,给它另做一个大 b。 知道了这个结论之后,我们来观察一下 an 方前面的系数就是公差的一半,所以见到这种题,先找 an 方, an 方前面的系数是一,所以我可以得到 d 等于两倍的疑就是二, 然后 s 一和二一相等,把一往里边一带就是三,那么通向公式自然就求出来了,当然这是小题,我们可以这样去秒杀。那么如果是大题该 该怎么办呢?考试当中出现了这样的题目,我们应该如何去处理?常规的方法,已知 s n 等于 n 方加上 r n, 我们需要把 s n 简易写出来, 我想学校的老师都给大家讲过已知 s n 求 n 的方法, n 等于 s, n 减去 s, n 减一, 化减之后得到二, n 加一,当然这是在 n 大于等于二的前提条件之下,然后需要算一下啊,一 啊一是等于 s e 的往里边一带等于三,然后再看一下 n 大于等于二的时 后,这个通向公式,当 n 等于一的时候,看一下他,当 n 等于一的时候,算出来也是三,所以他们两个结果相同,可以把他们合并为一个公式。 最后求出来啊, n 等于二, n 加一,和我们刚才的结果完全一样。同学们,今天的小技巧,你学会了吗?
 00:31查看AI文稿AI文稿
00:31查看AI文稿AI文稿干什么?干什么?怎么这种题你还是不会等他数列的通向问题,等他数列前文像和 s, n 等于二分之 d 乘以 n 的平方加上。不了,不了不了,后面就不用管了,看这个 n 平方前面是不是十二分之一。所以看到第一个 n 平方前面是三,那么他就是六。 n 把一带进去, a 一等于一,那么他就是六。 n 减五。第二个 n 的平方前面是负一,那么说明他就是负二。 n 把一带进去,他是一,那么就是负二。 n 加三。第三个 n 的平方是一,那么他就是二。 n 把一带进去,他是负一,那么是二。 n 减三,把七带进去就是二。乘以七减三等于十一。
139楠森π 03:50查看AI文稿AI文稿
03:50查看AI文稿AI文稿我们看解答题十七题的第一位给了一个 sn, 是 an 的前向和 a 一等于一 snban, 这个数列是公叉为三分之一的等叉数列,那么我们可以首先求出他的手下 是 s 一比 a 一,也就是 a 一比 a 一等于一。这样的话,这个数列就是一个首相为一,公差为三分之一的等差数列。 根据等差数列的通向公式,可以求出 snban 等于一加三分之一倍的 n 减一,也就是三分之 n 加二。把 an 乘到右边去,可以得到 sn 等于三分 之 n 加二倍的 an, 这是 sn 与 an 的关系,是要求 an。 我们一般往前写一项,也就是 sn 减一,那么他等于三分之 n 加一倍的 an 减一。 由于这个下标出现了 n 减一,所以我们后面要注明 n 大于等于二。然后我们让这两式相减,可以得到 sn 减。 sn 减一,等于三分之 n 加二倍的 an 减去三分之 n 加一百的 an 减一,而 sn 减 sn 减一,就是 an 给他一项,把 an 合并一下整理,可以得到 减一倍的 a, n 等于 n 加一倍的 a, n 减一,于是 a n b 上 an 减一,等于 n 加一,除以 n 减一, 这个也是在 n 大于等于二的前提下得到的。由于相邻两项相除后一项与前向的比是一个含有 n 的式子,这种情况我们适合用耒乘法来解决, 可以把 an 写成 anban 减一,乘以 an 减一, ban 减二,乘以 an 减二, ban 减三, 以此类推乘下去乘到 a 二比 a 一,然后再乘以 a 一。这样的话, 这里边互相都抵消掉,就可以只剩一个 an。 那么由于转化成了这些比例是互相乘机,都可以画成上面的这个 n 减一,分之 n 加以, 于是等于 n 加一。比上 n 减一,乘以 n 比 n 减二,乘以 n 减一,比 n 减三,以此类推,乘到三比上一, 再乘以 a 一,也就是一。这样我们会发现他是隔一项削掉一个,于是 n 减一, n 减二, n 减三,一直到三都能抵消掉。但是分子上会剩两项, n 乘 n 加一分,母上也会剩 两项,是二乘以一,于是等于二分之 n 乘 n 加一。由于这里的 an 是在 n 大于等于二的前提下得到的,那么我们需要检验一下 a 一 a 一等于一, 把一带入这个式子当中,是一乘以二除以二等于一是符合此事的。于是 an 的通向公式就是,二分之 n 乘 n 加一。
1258袁来有数(高中数学) 06:01
06:01 01:10
01:10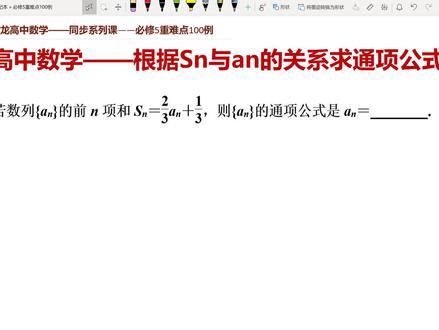 01:54查看AI文稿AI文稿
01:54查看AI文稿AI文稿我们来看一道根据 a n 与 sn 的关系求同项的题目,那么一个条件,给了 sn 等于三分之二, an 加三分之一,然后求同项 a n。 那一般情况下呢?根据这个表达是我们要分两种情况。首先当 n 等于一的时候, 等于一的时候呢,那么 s 一就是 a 一,他就等于三分之二, a 一加上三分之一,所以我们求出 a 一就等于一。然后第二种情况,当 n 大于等于二的时候,这个时候我们写两行,第一行就是已知给的这个条件。 第二行呢,我们把上面这个 n 都换成 n 减一,是不是就等等于这个?那么这是两个式的,一式和二式,我们用一式减二式,左边两个相减 s, n 减 s 减一,就是 a n, 右边的相减是三分之二, a n 减去三分之二, a n 减一。 整理一下,我们得到是多少呢?这是移过来是三分之一, a n 等于三分,负的三分之二也减一。在两边同乘,同时乘以三,得到 a n 就等于负二倍的 a n 减一,那说明什么?是不是说明这个数列 后一项与前一项的比值等于定值负二。那这里边呢?我们看,因为 n 大于等于二,当 n 等于二的时候,是正好是 a 二比 a 一,也就是对一切的这种是 n 都是成立的, 所以这个数列 a n, 他就是一个什么挡笔数列手相,手相是 一,公笔是负二,所以他的通项应该等于什么呢?一乘以负二的 n 减一次方好,这就是他的结果。
244延龙高中数学 02:51查看AI文稿AI文稿
02:51查看AI文稿AI文稿十九题的第一问,我们证明出了数列 b n 是首相为二分之三,公差为二分之一的等差数列,那么根据他的首相和公差,就可以求出 b n 的通项公式。 根据 b n 等于 b 一,加上 n 减一,乘以 d, 可以得到 b n 等于二分之三,加上二分之一倍的 n 减一,也就是二分之 n 加二。我们把 b n 的通向公式带入进这个条件,可以得到 s n 的关系。 sn 分之二,加上 n 加二,分之二等于二,那么两边约掉一个二以后,给这个移向到右边,然后就可以求出来 sn 的表达式。 sn 等于 n 加一 分之 n 加二,那 s n 为竖列 a n 的前向和。现在让我们求 a n 的通向公式,这是一个已知 s n 求 a n 的题型。首先,当 n 等于一时,我们可以先求出来 s 一,也就是 a 一, 他等于把一带进 sn 的这个公式,那就是二分之三。接下来,当 n 大于等于二的时候,我们的 a n 就等于前 n 向 s n 减去,前 n 减一项和 s n 减一。把 s n 的式子带入进去,就等于 n 加一分之 n 加二,减去 n 分之 n 加一,通分化减得到负的 n 乘 n 加一分之一。 而这个式子呢,是在 n 大于等于二的前提下求出来的。而我们之所以这里要写 n 大于等于二,是因为这里下标涉及到了 n 减一,如果 n 等于一的话,这里会变成 s 零,这是没有的。 所以在 n 大于等于二的前提下,求出来一个 a n 的通向公式。那么 a 一这个符合这个式子吗?我们来检验一下 a 一,本来我们求出来是二分之三,但是如果把 n 等于一带进这个里边,应该是负的二分之一 和本来的 a 一是不相同的,所以 a 一等于二分之三是不符合此式的。既然 n 等于一的时候,不符合 n 大于等于二的式子,我们对 a n 的通向公式就要采用分段的形式 来表达。 a n 等于分两段, n 等于一的时候就是二分之三。 n 大于等于二的时候是负的 n 乘 n 加一分之一, 那么从求出 sn 开始,一直到后面求出来 a n, 这就是一个典型的已知 s n 去求 a n 的类型。
347袁来有数(高中数学)
猜你喜欢
- 1314云帆
最新视频
- 2.8万张小知










