粉丝1372获赞5762
相关视频
 03:14查看AI文稿AI文稿
03:14查看AI文稿AI文稿各位好,我们介绍一下麦纳,我们波特图的一个位置,那么波特图呢?是我们在这个看系统的一个浮云图形的时候呢,是经常用到的一个,然后 然后跟我们之前的这个莱克斯特选图也是一个经常经常用,用来判断系统稳定性的一个方式,那么波特图它是系统平均响应的图纸方法,波特图呢是由福字图跟象字图组成。好,我们首先看一下我们怎么来绘制,那我们首先定一个微风扇子, 我们定一个传函 h s, 等于就是我们定一个这个一除以这个啊,一除以这个 a 视频,然后我们定一个这个, 呃,宽线完结应除以这个 ts, 嗯,零点一乘零四加加一,然后我们用波特图的一个这个,嗯,自带的一个波特,让我们进行回正, 我们共享一下屏。 好,那么我们可以看到,那么上面的是他的一个啊,扶贫特性啊,上面的是他一个复制图,下面的是他的一个啊,这个 这个一个向位图啊,看一下,那么上面是福字图像,下面是一个象脚图,那么两个两两,两者都是按这个频率的对数分度分割啊,分度可以是,那么波波的图也长,称为这个对数坐标图啊, 常称为这个对数中标图, 那么我们其实也可以啊,对他进行多种设置,对吧?我们也可以啊,进行设置远程坐标, 我们也可以设置他为这个设置他的横中坐标为赫兹,对吧?我们可以 pro pro practice, 然后我们可以设置他的一个优点,是啊,我们的他人坐标为赫兹也可以。好,然后我们将 说我们复制啊,复制,我们不想让他用封面显示,我们绝对值显示也是可以的啊。然后,然后我们的这个,呃,这个,这个波特的这个坐标,坐标也是可以在图上改的。好,然后这就是一个波特图的一个绘制, 然后呢? photo 图呢?是用 mind 绘制的话啊,你可以这个, 呃,方便我们这个利用这个开关系统函数来分析这个变换系统稳定性的一个方法。好,那么谢谢大家。那么这是一个一届的,大家可以看到这是一个一届的一个关键问题,一键的一个关键问题。
 08:18
08:18 01:10查看AI文稿AI文稿
01:10查看AI文稿AI文稿这几天搭建了个三项车整流器,使用帕泽劳进行环路补偿设计,使用零极点匹配法以及系统稳定判决。 这是电压外环开环爆布。这是电流环零极点还原 p i 系数。 现在我们把计算出来的次数放到 brt 控制器里看看效果。 运行仿真过程有点久,我们快建议啊。 这是最终效果,零点一秒处加了个节约负债。左下角是三相电流稳定响应。
230波仔不是啵啵 06:52查看AI文稿AI文稿
06:52查看AI文稿AI文稿大家好,这节课给大家介绍一下麦特老板当中的绘图。那首先 我们先定一遍,那么我 定义了一个变量 a, 然后定义了一个变量 y, 那么 y 呢?是等于三 a 的,也就是说 y 对于 a 的某一个资本量,他返回的都是一个三元 a 的一个结果,那这边我们再用 plut, 对啊这个 y 进行一个绘图,那么横坐标是 a, 重头标是 y, 我们不落的 a 以外就会得到这样的一个结果。那么呃大家可以看到这是买三个当中的图形界面的一个窗口,那这边会有很多的一个操作,像文件啊,编辑啊,呃这里的,那么我们在编辑这边我们可以看到啊,就是对 很多的一些呃参数进行一个编辑,像轴啊,图形之类的,那我们点开这个图形属性或者轴属性呢,我们就可以对这个轴上面的一些东西,或者是图形上面的一些东西进行一个编辑。那么 还有比如说像插入之类的,我们如果说要插入一些图力啊,或者说呃插入新的一个坐标轴,我们要放一个局部的一个图的话,那么可以通过插入这方面啊的一些操作来够达到我们的一个目的。那这边我就简单 介绍一下,就是呃如何用 pro 的,就是来呃会一些就是比较好看的图吧,那么呃 polt 的话,我们 可以看到非常简单的,我们通过测评量和音变量的一个数据,我们就可以画出一这么一幅简单的图,那么我们还可以通过一些其他的参数来调整这个图的结构,那这里我们已经扑了它之后我们 再拨开一下 a y, 我们现在想要把这个线条变粗,那么我们需要调这个属性, 先输入属性名,属性名是蓝外,就是一个线宽,线宽他原本的线宽默认是零点五线宽,我们调成十二,我们看一下这个图上的一个结果,大家可以看到我们这 图啊,他确实是变粗了。那这边呃大家可能会想一个问题,就是说我现在这个 plut, 原来这个 plut 是一个 啊,覆盖的一个关系,还是说原本的 polt 的图形被清除了,而现在显示的是我们这么一个呃 polt 的一个结果呢?那我们可以通过比如说呃 y 一等于一加二来看一下这个结果是怎样。如果我们 pro 等一下 你调成什么我看一下 啊,我们可以看到啊,这个确实是把原来我们绘图的一个结果给清除掉,然后画上了这么一幅新的图, 那这是我们的绘图那个基本特写。如果想要嗯在原来的图上结果继续画图的话,那么就是 hold ololo, 那么来 olol, 输入 holol 之后,我们再呃来普洱腿下, 哎倒外就是刚刚那个正那条正弦曲线,那么再给大家看一下他还有一些其他的呃属于特性,那么最经典的就是对 线条,比如说我们这个是实线,对吧?我们可以把它变成虚线,或者说是系列画线之类的,以及线条的颜色,那我们可以这样子,就是直接在一个呃双引号,呃两个单引号之间直接给他解决掉,那 输的第一个参数是呃颜色参数,那么二对应的就是这个 red 这个英文单词一个 呃第一个字母,那么这个就定义了它的颜色是红色,然后我们嗯线条长什么样?线条呢?它是一个呃虚线,那么如果我们要是细点画线呢?就是加个点 啊,然后还有一个是图形的标记,比如说我想在图形上面标个小圆圈,那么再加一个 o 啊,然后我们再看一下这个结果, 可以看到这边呃已经是红色的,然后是呃他确实是这个细点画线,然后是 啊欧的这种情况,但是由于这个数据点比较密集啊,有一千多个数据点,所以说这边我们肉眼上看过去,其实就是像比较看上去就比较连贯,难以看清楚他的细节,然后把放大 可以看到,对吧?把它放大之后确实是一个呃红色的一个,然后是细点画线,然后他的标记是一个圆圈, 那么然后我们想画图的话,就是不希望在在覆盖原来的这个图像, 然后我们就薅到二,那就结束了,结束这个呃,然后再铺上来一二三四五六,那就是这么一个简单的一个图了, 那这是一个基本的一个绘图情况的。还有个 svboybook sligw ylego 呢,是用来设置这个轴和轴两个轴的一个名称的, x 轴的名称,外轴的名称,然后如果是三维的话有个 zlebo, 那还有一个是开头, 这是我们的一个,就是这个轴轴的这这个图像的一个呃标题的胎头 abc, 就可以得到这个 abc, 这个胎头啊,其实还有更多的属性,大家要深入了解的话,可以通过我们这个 dm, 就在第一节课我也给大家讲过啊,这个呆木这边有一个啊,古拉菲,古拉菲克下面有很多的一些绘图的一些内容啊,因为我们这个绘图其实不仅限于就是会这种啊,常规的这种啊,二维啊三维的同学还有很多企图呢,根据不同的学生看 不同的要求吗?所以说,呃,大家需要就是深入了解这个的话,就需要在单幕里面查看跟自己专业相符的一些内容啊。那这一份的话就给大家介绍这些,再见。
156我不是Matlab 00:10
00:10 02:12
02:12 01:08:29
01:08:29 07:36查看AI文稿AI文稿
07:36查看AI文稿AI文稿今天我们一起来学习 matalabe 三维曲面。在上一届我们介绍了绘制三维曲线的方法, 这一节我们学习如何定义空间网格上的数据点坐标,并绘制三维曲面。通常曼特拉布中绘制三维曲面图,先要生成网格数据, 再调用魔石函数和 soft 函数绘制三维曲面。在曼特拉布当中产生平面区域内的网格坐标矩阵有两种方法,第一种方法是利用矩阵运算生成,我们来看一个例子,首先创建 二、三、四、五、六共有五个元素的含香量 x, 再创建 三、四、五、六、七、八共六个元素的列项量 y, 矩阵 x 的每一行都是项链 x, 行数等于项链 y 元素的个数。同时矩阵 y 的每一列 都是项链 y, 列数等于项链 x 的元素的个数。我们把这个命令在马特拉卜当中运行,这是运行的结果,会看到 矩阵 x 是一个六行五列的一个矩阵,矩阵歪也是一个六行五列的一个矩阵。这个时候矩阵 x 和矩阵 y 相同位置上的元素,比如说矩阵 x 上的 x 三二,第三行第二列的元素三和矩阵歪里的 y 三二,第三行第二列元素上的五就是区域第三行第二列网格点的坐标三五。对于平面网格矩阵生成的第二种方法是用莫斯格瑞的函数生成, 这是莫斯格瑞的函数的格式,其中小括号里的 xy 为项链存储计算结果的大 xy 为矩阵存储网格点的坐标。这里的第 三行命令生成的网格坐标矩阵 x y 与方法一得到的结果是相同的。我们来看一个例子,在这个命令当中,第一行命令是创建二、三、四、五、六共五个元素的行项链 x。 第二行命令创建三、四、五、六、七、八共六个元素的列项量 y。 第三行命令,利用莫斯格瑞的函数生成网格矩阵。 第四行命令,利用 red n 函数生成与 x 同型的矩阵 z, z 的大小也是六行五列。第五行命令利用矩阵 x, y, z 作为参数。第二,用 plot 函数绘制图形。我们把这个命令在曼特拉伯当中运行,这是运行的结果,可以看到有五条曲线。 下面我们再来学习绘制三维曲面的函数。巴特那不提供了 mose 函数和 soft 函数来绘制三维曲面图, mose 函数用于绘制三维网格图,而 sof 函数用于绘制三维曲面图。 各线条直接的补色,用颜色来填充。一般情况下, xyz 三个参数是同形的矩阵,其中 xy 是网格坐标矩阵,这是网格点上的高度矩阵。 c 利用于指定在不同高度下的曲面颜色 c 省略时,玛特拉不认为 c 等于 c, 也就是说颜色的设定是正比于图形的高度。这样就可以得出层次分明的三位图形。 下面看一个例子,绘制三维曲面图,这是定义的曲面的方程,这是第二用的命令。 在这里要用三个函数来绘制三位曲面图,一个是 mose 函数,一个是 surf 函数,一个是 plot 三函数。 我们同样把这个命令在马特拉布当中运行,这是运行的结果。从图中可以发现,在子图一当中,第二用的是魔石函数,有魔石 函数绘制的网格图,线条有颜色,线条界的补面没有颜色。在子图二当中,第二用的是 suf 函数。 suf 函数绘制的曲面图,它的线条是黑色的线条补面有颜色。 还可进步观察。曲面图补面颜色和网格图的线条颜色都是沿 c 轴变化的。 在子图三当中,第二用的是 plot 三函数, plot 三绘制的三维曲面实际上是由三维曲线组合而成的。 再来看绘制三维曲面的其他函数,和魔石函数相似的两个函数分别 是 mc c 和 mcz。 mcc 是画带等高线的稍微网格曲面函数。模式 z 呢,是画带底座的稍微网格曲线函数。 用法与模式相同,不同的是,模式 c 还在 x y 平面上绘制曲面。在 c 轴方向的等高线 耳膜是 z 呢,还在 x y 平面上绘制曲面的底座。和 suff 函数。类似的两个函数分别是 suff c 和 suffle l。 斯夫 c 是画具有等高线的曲面函数, sfl 呢,是画具有光照效果的曲面函数。下面看一个例子,用四种方式绘制函数,第一 命令调用莫斯格瑞的函数生成网格矩阵 xy, 第二个命令生成高度矩阵 z。 后面的命令分别调用 mercie、 mercize、 serf sea 和 self l 四个函数绘制曲面,并且给图形添加对应的标题。我们把这个命令在曼特拉布当中运行,这是运行的结果。对比发现,在子图一和子图三当中 都有等高线,只图二当中有底座,只图四当中有光照,效果好。这就是今天的内容。马特拉布三维曲面的绘制方法就讲到这里,谢谢大家。
411朝霞szx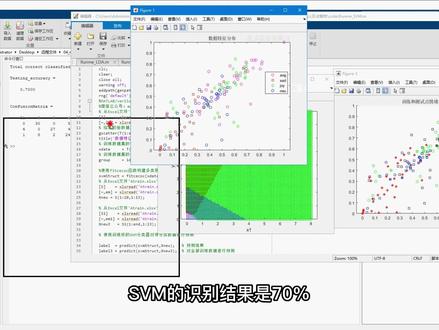 01:36查看AI文稿AI文稿
01:36查看AI文稿AI文稿哈喽,大家好,我是简简单单做算法,今天我们介绍三个常见的机器学习方法, 对数据进行分类和识别。这三个方法分别是 l d a, s v m 以及决策术。 我们首先运行 l d a, 这个是 l d a 的一个识别结果,它对数据的识别正确率只有百分之六十。然后我们打开决策数, 那么决策术的识别率是在百分之八十五, 这个是决策书的最终识别结果。最后我们运行 s v m, 这个是 s v m 的识别结果, s v m 的识别结果是百分之七十。那么这里性能就是 决策术用于 s v m u 于 l d a。 演示完毕,谢谢大家。









