DOE在六西格玛一书中的哪一个章节?
粉丝6437获赞1.4万
相关视频
 05:56
05:56 12:40查看AI文稿AI文稿
12:40查看AI文稿AI文稿哈喽,大家好啊,这期视频是六七个马黑带考试题解析的第十集啊,丢一,实验次数的计算啊。说到实验设计,丢一很多人都很清楚,这是六七个马 管理学的核心内容啊。的确啊,实验设计的应用已经从一般的制造业的产品质量改善和工艺流程优化发展到了生物制药、科研公关和医疗创新等尖端的领域。 如果你在一个野金行业,那么你通过实验设计可以将钢铁野链的原矿石的利用率提高几个百分点。 那么如果你在的是食品制造行业或者是调味品制造行业, 通过实验设计,你可以将啊,比方说酱油的发酵的产量提高一定的比例 百分之五或者是百分之八,这样听起来是不是啊,非常具有诱惑力,但是你要具备这种能力并不是一朝一夕的事情,那我们要从实验设计的基础着手,一步一步的来, 那通常规划实验设计的时候,都会设计到我们要做多少次实验才能达到我们的实验目的,那么究竟要做多少次实验呢? 在六七码管理中,这个是非常讲究的,我们不能少做,当然也没有必要多做。那么有些人会说啊,多做了没关系啊, 但是在我看来啊,如果你可以忽略所有的成本的话,那多做几次的确是没有关系,但是啊,我下面给大家举几个例子,大家来看一下。在这些实验中, 成本因素是你不得不考虑的,那比方说啊,我们这个农田水稻的实验 啊,先不谈其他成本,他实验周期的话都要三到五个月一次。 好,那我们再举一个啊,生活息息相关的例子,比如说你经常吃的调味品啊,酱油, 他的发酵实验的周期是需要一到三个月,那么啊,在 比如我们的啊,重型的行业,钢铁行业啊,如果你要做野金的实验的话,你就必须得清楚,例如铁水他最少也要九十吨,那么 啊,像以上的这么多实验,这些时间和物质的成本他都是非常昂贵的, 所以我们该做几次实验呢?我们一定要算的清清楚楚。好,下面我们就通过两个考试题目来一起讨论一下如何准确的计算实验的次数。 好,我们下面来看到题目第一题,项目团队为提升钢体钢孔直径的合格率,对已确定的三个因子,在 改进阶段运用丢衣实验寻找最佳改进方案。三个因子是连续数据,每个因子取两水平,仿行两次,考虑白斑和夜斑生产预分两个区,每个区主中心点为三, 这实验的总数应该是多少?好,我们看到这个题,它是一个全因子实验次数的一个计算啊,全因子实验设计的次数的计算,它有一个公式 啊,这个是我专门为大家总结的,他就等于二的啊,因子的个数次方乘以仿型的次数, 然后加上驱阻数乘以中心点数。啊,这个按照这个公式计算就可以准确的算出来啊,我们 要做多少次实验?好,我们看到题目中啊,他是三个关键因子,所以这个因子个数次方应该是三。仿型次数,仿型两次区组数预分两个区组 中心点数,中心点数为三。好,所有的都是已知的,那我们算出来应该多少?二的三次方乘以二等于十六,加上驱逐数二乘以啊,中心点个数三六, 是不是最后结果等于这个 b 二十二,他总共要做二十二次实验。好,如果你觉得这个公式理解起来比较困难。好,我下面还有详细一点的资料,大家可以参考一下。好,这里的话,我啊把重点的句子给大家挑出来啊, 希望大家能够把剩余的在呃课余的时间可以看完。好, 中心点,我们看到中心点他是检测响应中的弯曲,然后他还可以啊,来估计变异性。好,然后我们再看到 啊脚点仿型术,脚点仿型术它是什么目的呢?它是啊,可以帮助你提高模型的精度 啊,因为啊,每增加一次发型,他就啊同样的实验,他就要重做一次,所以他可以提高精度。好,我们再看到区组数 驱阻术,这个是比较容易混淆的,他是在不同条件下 执行流程之间可能发生的差异啊,比方说我们做一个实验要做十次啊,要做十个实验,这十个实验本来是一起完成的,但是啊,你一天只能完成啊五次实验, 那么剩余的五十要在第二天。好,这样的话,我们啊今天和明天啊,第一天和第二天之间, 天气啊,温度和湿度的变异,是不是就会对实验结果产生影响啊?虽然说我们不纳入到因此,但是我们这个要考虑进去,所以我们就把它分成两组,那这个就要驱逐。好,我们看到下一题, 我们看到第二题,在实验设计中要考虑 abcd 一五个因子,同时需要考察二阶交互作用 b 及 bc, 满足此要求的实验次数最少是多少次?好,这个题目呢,它是一个部分因子实验次数的计算,部分因子实验次数的计算主要分为两步, 那么第一步是找到他音质的个数和分辨度,第二个就是查表。好, 我们看一下他的因子个数啊,题目中给的五个,然后要分辨度呢, 分辨度他没有直接给出,他是这样提供一个条件的,同时要考察啊,两阶交互作用 ab 及 bc 啊,这句啊,其实他就是 告诉你分辨度要为多少,知识点都在书上,那我带大家啊,把这个知识点给了解一下啊。分辨度, 我们常用的分辨度啊,主要有分辨度三、分辨度四和分辨度。那么分辨度三他的混杂情况是什么样子呢 啊,他是主效应与主效应之间没有混杂,就是 a 和 b 因子啊,两个是没有混杂的,那么主效应与二因子交互作用 啊,影影响他是混杂的,就是说 a 和 bc 啊之间他是混杂的,所以 啊,这是分辨度三的情况。那么分辨度四呢?分辨度四是主效应之间和啊,主效应与二阶之间是没有 有混杂的,但是二阶之间他是有混杂的。好,是不是情况越来越好啊, 那么我们看到分辨度,他是主效应与主效应之间,主效应二阶和二阶和二阶之间都是没有混杂的,但是他的二阶与三阶之间的作用是影响是混杂的。好,知道这些以后,我们再联系题目, 他要求二阶与二阶之间是没有混杂的,所以我们只能选分辨度,那么我们还有知道了这些啊条件之后,我们还要依赖这张表 啊,这张表的话,他的第一行是音质的个数,那么他的这一列就是我们最终要做实验的次数,中间的话就是 分辨度啊,我们刚才是 abcd 一五个因子,所以我们在这一列,这一列的话,我们题目要求的是分辨度是几啊?分辨度是五,所以我们找到这个位置,然后看一下 他要做十六次实验。好,所以这道题的结果应该是那十六次。好啊,下面我给大家演示一下这个 mini tibo 是如何操作的,其实如果你用 mini tibo 的话,这些都很容易解决。好, 我们打开 minitabo, 选择统计,丢一因子,创建 因子设计。我们第一题的话,是啊,选择两水平,然后他的因子个数是三个,我们看一下他的选项, 他是全因子,然后他的中心点数是三 脚点,仿型是两次,屈指数是二。好,把这些所有的参数都输进去,我们看一下计算出来的结果是多少,那在这边 检查一下,我们就看到实验的结果是多少次,二十二次。好,我们再看到第二题, 统计丢一因子,创建因子设计同样是两水平,但是他是部分因子,我们总共有五个因子,对应的是 这里,分辨度对应的是五。好,他的区中心点和脚点仿型是一驱逐数,中心点是零,然后驱逐数是一。好,我们再看一下运算的结果是多少次呢? 好,看一下最后结果是十六次 啊,与我们的这个是完全吻合的。好,以上就是本期视频的所有内容,还希望你已经通过这两个题目学会了 如何准确的计算实验次数啊,也希望你已经动手使用 vivo 软件,开始了自己的实验设计,更希望你能通过实验设计这个优秀的工具啊,为你所在的行业做出贡献, 为企业带来利益,为行业注入活力。好,本期视频我们就聊到这里,好,谢谢大家的观看。如果你对本期视频的内容还有疑问,或者是你还有啊什么其他新的问题, 都可以在评论区给我留言,或者是啊发邮件到下面这个邮箱 啊,我会及时的给出回复。好,如果你身边还有其他正在努力学习六七个码管理的小伙伴,如果你觉得这个视频还是比较有帮助的 啊,希望你动动手指转发分享给他们。好,最后祝大家能够在六星马黑带考试中取得优异的成绩。
155James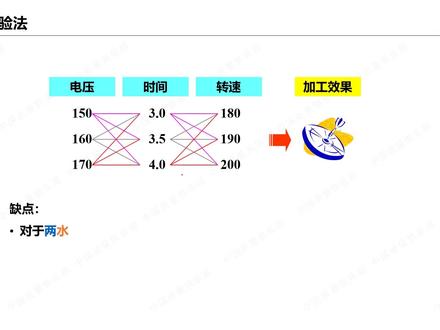 15:00查看AI文稿AI文稿
15:00查看AI文稿AI文稿次数过多,那另外呢,还有一个缺点呢,如果说我们的因子是两水平,比如说刚,当然这个案例呢,是三水平,如果我们只取两水平,他不一定能找到 最佳,比如说我们的量水平呢,是幺电压是幺五零幺六零,那在这个幺五零和幺六零之间就寻找不到试验最佳点,比如说一百五十二,那这个他是永远找不到的啊,当然三水平是可以的啊,那我们这块呢,就单独说一下两水平的一个缺陷啊。 好,那我们回到刚刚的那个汽车油耗的案例,那事故法呢,一次就做一次实验,而我们的这个单因子变化法呢,这个案例呢,做了十一次实验啊,而我们的如果说我们用 doe 可能做九次实验啊,找到的最佳的是七点零,而我们的呃一次因子呢,要做十一次实验啊。 到目前为止呢,我们的单一子变化法呢,已经是一个呃,怎么说呢,是一个被呃抛弃的一个实验设计方法啊,我们现在的 due 的大家族里面已经把他踢出出去了。 也就是说,呃,我们认为呢,单因子变化法呢,他呢必须有两个前提假定。 第一个呢,就是模型呢,基本上是一个偏线性的,也就说 x 对歪的影响呢,还是偏向于一个线性的变化,如果有非线性,他的非线性程度应该不是很高啊。第二个呢,这是最大的一个 bug, 就是说 因子之间呢,不允许有交互作用,一旦有交互作用的单因子变化法呢,是呃很难去研究的啊。所以呢,这两个假定成立的条件下,单因子变化法呢,他呢能够得到很好的结论,但通常情况下啊,这两个条件呢都是不成立的。 关于事务法呢,这个就更不用说了啊,我做过很多的,我带过很多的六 c 干嘛的项目啊,那有些学员呢就一直跟我说,哎呀,郑老师我们 呃能不能呃让我试一次哈,那我们做这个六四个卖项目呢,通常在顶麦克的 i 阶段啊,就是改进阶段啊,要用到这个实验了啊, 那我就在说啊,你这个问题已经困扰你一年了,半年了啊,甚至两三年了啊,你早如果能够 用事物法做出来早就做出来了。好,那不妨静下心来呢安排啊真正的这个实验啊,来去解决他。所以呢在这边呢,大家一定要相信相信科学的方法, due 的方法。 那在这边呢,我们的低优一呢到底有什么不同之处呢啊,也就是说我们的低优一的本质呢是只用较少的实验成本,也就是较少的实验次数啊,可以获得更多的 x 和 y 之间的信息,进而呢找到最优 那。呃如果说 使用失误法啊,很多人呢会觉得,哎失误法不错,我只要做一次,只要做一呃一次啊,然后 万一运气好就能拿到这个结论啊。但是呢如果说你有强迫症的话,那我想问你怎么能保证你拿到这个结论就是最好的呢? 那单因子变化法呢,他忽略了因子之间的交互作用啊,而这一点呢在我们的工程中呢是最常见的啊。如果说,呃在一个这个实力中呢,确实没有交互作用,反而单因子变化法的效率呢是比较高的啊。 呃所以结论就是永远不要使用事物法和单一子变化法。那我们来看,我们如果说要用科学的方法,那我们一定要借借助于统计学,那统计学在这边呢,给了我们一种科学的数据分析方法啊,他不仅仅是只看到 到了这样的一个现象,而且呢他要去找到啊,他的一个规律。我们来看,比如说如果说我们不使用同居学啊,我的一个呃速度对油耗的影响,我在八十和一百度下的一个变化, 我八十呃速度是八十的时候只做一次实验,得到了一个油耗的一个点,在这里啊,我在一百的时候又做一次,那我发现,哎,随着速度的增加我的油耗在减少。这个结论从食物上来看显然是错误的。 那如果我们多做几次,比如说在八十下我做了四次啊,一百下也做了四次,这个时候我们会发现呢,哎,我们的均值的变化是呈现一个上升的啊,而这块呢他会有一个波动的一个区间,那 我们把这个呢就叫置信区间啊啊关于这个统计学的置信区间的概念呢,我这边呢不想过多的介绍。呃如果对这部分呢,想要更多的了解呢,请关注我们啊俱乐部的其他的课程啊。 那统计学呢,他呢可以给我们很多的一些方法,比如说啊,一些重复实验啊,来增加我们的一个准确度啊,用随机化啊,减少某些未知的 趋势啊,用划分区组来了解一些噪声因子啊,那用分析因子设计,那提高我们的一个分析的效率,那回归分析和方差分析呢,用来客观评估啊,等等的,那这些内容呢,我们在后面呢会详细的讲到啊, 所以呢,最后我们总结一下啊, due 的一个优势啊,也就是说第一个呢,他是一个客观的程序,不是凭主观的一个判断啊。第二个呢,他的效率呢是最高的啊,大家千万不要迷信啊,什么单因子变化法,什么事物法, 那另外呢,他是一个系统的程序啊,也就是说,哎,我们可以借借助之前的经验和之前的一些历史的数据,都可以帮助我们去做我们的实验的安排,进而去分析数据,建立模型。 所以呢, due 想要取得成功,第一个必须要有专业知识啊,这个是必须的,如果说你只有指挥 due 的方法论没用,那你一定要知道 哪些是真是 x 啊,找到这些 x 啊,那要有正确的方法啊,那我们一定要注重统计学啊。第三个呢,当然呢,还要有资源啊, 呃,有时候我们经常听到一个呃,一些陈述,比如说我们没有足够的资源来进行低于一,所以我们可能需要用其他的方法啊,当然如果你用了其他的方法,有可能你需要的资源会更多 啊,比如说事物法,单因子变化法啊,所以我们一定要相信科学的方法。那我们六 c 的嘛的顶麦克的流程啊, dmvs, 我们在 i 阶段呢,通常呢会用到 due 这样的一个方法,所以呢,毫不夸张的说 due 是六 这个嘛抵卖个流程的最核心的工具啊,没有之一啊,同样的他也是的, fs 就六 c 个嘛设计的核心工具,当然这块要加之一 ok, 呃,最后呢,在这次课程呢,我们跟大家简单的演示一下啊,如何创建一个 due 的一个实验计划啊,比如说,我们先来读一下这个案例 啊,我们正好把之前的概念来复习一下,那这个案例呢,我们的指标歪是什么呢? 对了,我们的指标歪呢,就是成型塑胶板的强度,我们简称为强度。那 这块我们的 x 呢? ok, 我们有三个 x, 分别是压磨间距,压磨成型压力和压力角,我们分别记住 abc, 那每个 x 呢,我们取两个水平啊,低水平,高水平,比如说压磨间距的两个水平六十七十。 ok, 成型压力三百四百,压力角二十二十四。 ok, 我们来安排这样的一个试验计划啊,那我们这次课程呢,会用到这个迷你泰博软件。 呃,关于 minitty 软件呢,我不想太多介绍了,我这边呢用的是 minitty 十八版,当然目前最新的版本是十九版。 好,我们的路径呢是统计 pu 一,因此创建,因此设计啊,我这边暂停一下,大家可以看到这个路径 点开之后呢,我们会产生这样的一个界面啊,在这个界面里面呢,我们的因子数在这边呢要选三个啊,也就说我们这边呢是有三个因子,每个因子呢设定了两个水平。 这块呢,我们点开设计的按钮,我们先教大家全因子的一个创建方法,所以大家在这边呢勾一下全因子 啊,这些内容呢,我们到后面的课程再来介绍。所以这部分呢,大家先不改他, 我们就做一下三因子两水平的一个八次的一个实验配置,他的实验符号呢是二的三次方,就代表了是两个水平,三个因子,也就说每个因子都是两个水平,这样八次实验我们点确定, ok, 如果说点完之后呢,你会看到我们这个因子的按钮呢,就会呃显示出来,大家点开, 我们默认的是 abc, 低水平用负一,高水平用正一,这个就叫代码,代码值啊,我们先用代码值来创建一下看看啊, 然后我们点确定 好,大家会看到 我们这边呢,就把我们的试验配置就做出来了,当然我们在 c 八这个标题列这边呢,我们输一个 y, 这样的话我们就可以安排八次实验。当然我们的 doe 呢,这边呢,他把我们的这个试验顺序给打乱了 啊,这就是我们的八次实验的一个配置啊,那这边呢代表,比如说第一次啊,我们的这个第一个实验呢,就是我们的 a 因子取高水平, b 因子取低水平,而 c 因子取低水平,我们就可以做出产品来, 最后呢测出他的强度值,把它输入到这里来啊,当八字实验做完,那我们就可以去分析数据,这就是我们的实验的一个配置。当然呢有人说,哎,老师,我们这边呢, a 因子是压磨间距,成型压力,包括他的高低水平,能不能输入进来呢?我们讲当然是没有问题的啊,那我们在刚刚的路径 啊,在统计 due 因子,创建因子设计这块,我们可以点开这样的一个因子的按钮,我们在这块呢,把这些因子的名称输进来啊, 比如说压磨间距,成型压力啊,压力角, 那淹没间距啊,我们来看一下他的高低水平,六十七十三百四百二十二十四啊,六十 七十三百四百二十 二十四啊,注意这块呢,呃,千万不要去输单位啊,只要输他的数值啊,点确定, 当然我们直接点确定他会做出来啊,刚刚呢我们在这块呢是把他的呃没有给他呃排顺序,那我们如果点开选项,我们的软件默认是随机化运行顺序的,如果你把这个小勾去掉,哎,他这个顺序呢, 你做出来的这个顺序和我做出来的顺序都是一模一样的。那我们这次呢讲解的时候呢,我们把这个随机化运行顺序勾去掉,我们点确定 好,我们在这边呢,我们输一个强度, ok, 大家会看到这就是我们的实验的计划表啊,在这块呢,我们前面这些东 东西呢,大家先不用管他,后面我们会来讲,呃,这次呢我们先把 c 一和 c 二说一下, c 一呢叫标准序,就是没有随机化的一个顺序, 而 c 二呢运行序啊,他永远是从一到八啊,那关于中心点和区组呢,我们到后面的课程再来介绍啊。 那呃如果说我们随机化顺序之后呢,这个标准序就会打乱,但是运行序呢永远是一到八啊,那我们的实验的时候呢,一定按照运行序来做实验,那这就是后面我们会讲到实验设计的其中一个原则呢,叫做随机化 啊,我们看一下啊,如果说,哎,在这边呢,我们还是刚刚创建因子设计,我们可以点开选项,把随机化顺序呢勾出来,点去 确定,再点确定, ok, 我们这样做出来的标准序会打乱啊,我们按照运行序来做实验,这就是随机化啊,当然我们可以在这块输一个强度 啊,这就是我们的一个实验计划表。 好,我们来回到我们的课程讲一 那这样的一个三因子两水平的一个设计,这就是我们的全因子设计。 全因子设计我们之前说过啊,他的一个好处呢,就是说,呃,他能够估计交互作用啊,所以呢,我们可以去判断哪些变量的主效应是显。
 15:00查看AI文稿AI文稿
15:00查看AI文稿AI文稿我是本次课程主讲老师正派,我们的课程呢是实验设计 d u e 的系列课程,那 d u e 叫抵赞 exparmex, 也就是我们翻译过来就叫实验设计。 那我们的课程的学习目的呢,主要有以下五个方面,第一个呢,是了解什么是试验和他的必要性。 第二点呢,理解 due 就是我们的试验设计相比于其他的传统方法的优势和 due 成功的因素。第三个呢,了解 due 使用的一个基本的一个流程和套路。第四个呢,就是我们的课程呢,主要讲三种方法, 一个叫全因子设计,第二个是部分因子设计,第三个是小型曲面设计。最后第五个方面呢,就是希望大家呢,能够将 do 一的这个理论呢,应用于实际工作中,去解决实际过程工作中的一些问题。 我们的课程呢,一共十二讲啊,每一讲呢,大概一个小时左右。 那第一讲第二讲呢,主要是介绍一些低于一的基础,包括一些名词术语,以及我们会跟大家补充像方查分析啦,回归啦等等这些内容。从第三讲开始。呃,三四五呢,主要介绍的是全因子设计啊, 全因子设计呢,我们会重点介绍数据的分析的方法。呃,六七八三讲呢,我们会介绍部分因子设计。 这部分呢,我们呃会重点讲如何去配置实验计划表。 那九十十一三角呢,我们介绍的是小型曲面设计啊,我们会跟大家重点介绍中心复合实验设计也会讲到啊, bbd, 我们叫 box bicon 设计。最后第十二讲呢,是一个整体的总结和案例的一个讨论。 我们先来进入第一讲实验设计基础。一, 我们这个课程呢,这一讲呢,主要是四个方面的内容,第一部分呢,介绍 doe 的历史,第二部分介绍名词术语,第三部分介绍 doe 的必要性,第四部分呢,我们简单的跟大家做一个全因子的设,我们先来看什么是试验, 如果我们把我们要研究的对象或者是系统呢,看作是一个过程,那对于一个过程呢,会有输入和输出,输出呢,我们称之为响应,而输入呢,我们称之为自辨量, 在这块呢,我们用眼睛来观测到的就是响应,而我们用手可以改变的,哎,就是自辨量, 这一点呢,非常关键。我们在做实验设计的时候呢,一定要明白我们本次所课程所介绍的 die, 他针对的一个系统的, 他的输入呢,是可以直接来改变和设定的,而他的输出呢,不能这样做,输出呢,只能观测到, 如果想要改变输出,那必须通过去调整输入来改变。举一个例子, 我们做一个机加工,哎,我机加工的,呃,比如说车靴啊,我的车靴的速度啊, 行进的一个行程啊,这些呢,都是我们的设定,是我们的输入,而最后我测出来的产品的,比如说外镜啦,哎,长宽高啦,这些东西呢,就是我们的输出,我们用测量的方式来测出来。我们再举一个例子呢,比如说我们的一个焊接的过程, 那我焊接出来的产品上的特性,比如说我的产品的一些强度,焊接的产品的质量,外观,那这些呢,都是观测到的啊,就是我们的输出或者叫响应,而我们的输入, 比如说我焊接的时候啊,用什么样的焊材,哎,我的这个焊接的温度啊,电流,电压,焊接的时间,这些呢,都是输入,就是我们的自便量,而这些输入我们可以直接去调整,设定和改变啊,这是非常重要的一个概念。 我们来看 d u e 的历史,那 d u e 的名词的提出者呢,是菲显,他也是我们普遍认为呢是 d u e 的最早的一个奠基人。 那菲士尔呢?当年呢,在研究这个田间实验啊,就是包括水稻的育种啊,这类的研究呢,提出了一些方法论,那他把这个方法呢称之为 doe。 呃,随后呢,在上世纪五十年代呢,天口玄鹰呢, 呃,他提出了早期方查分析的不足,并且呢提出了正胶实验设计法,有说正胶表并不是甜口提出来的,但是呢,他是将正胶表用于试验设计的第一人啊,所以呢,他是正胶实验设计的提出者,那这样的话, dv 呢,就除了全因子啊, 那产生了部分因子设计。当然呢,之后呢,还有很多的学者的一些补充啊,包括我们这次还会讲到强音曲面设计,那除此之外呢,还有很多很多的设计方法,那我们把这类设计的方法呢,统称为经典 doe, 或者有些人称之为传统 doe。 所以呢,这是 due 的其中一个流派啊,那另外一个流派呢?呃,代表人物呢是舔口悬疑啊,上世纪六十年代呢,他,呃从这个 经典流派啊脱离出来啊,他提出了他著名的一个观点叫呃质量损失函数啊,他的一个质量的一个观点,进而建制了文件参数设计的方法啊,呃, 这些方法论呢,成为呢呃很多的一些企业呢所采用,尤其像日本当时的这个丰田公司啊, 那之后呢,填口呢,不仅呢发展了他的这个文件参数设计,他还提出了三次设计的概念,包括系统设计,参数设计和容差设计。所以填口方法呢,文件参数设计呢,是其中最重要的, 但除此之外呢,还有其他的像荣叉设计啊,那呃之后呢甜口呢,在这个他还 提出了一个动态的参数设计方法,也就是说它包含了静态和动态两类方法啊。当然本次课程呢,我们呃不会来介绍这个填口方法,我们重点还是介绍经典定义。 呃,另外呢,在一九七八年呢,是由王源和方开泰教授呢提出了这个均匀实验设计法,这可以称之为是 dv 的第三个流派啊,那均匀实验设计法呢?呃, 应该来说呢,是我国,我们国家的数学家发展了这个华罗庚的很多的一些数学思想啊,在数论的基础上呢,提出了一种仿蒙的卡罗的一个算法啊, 进而提出了这样的一个均匀试验设计法,那目前呢,主要还是用在军工行业啊,这个呢,可以认为是第三个流派。 我们来看第四个流派啊,这两年可能呃筛令丢一啊,我们叫谢宁方法,或者叫谢宁实验法,或者有些叫谢宁丢一啊,这个方法呢,目前被很多公司呢有所应用啊,在德国的很多企业呢会叫 redx 红 x 技术啊, 这套方法呢,呃,他其实是呃系统解决问题的一套思路和方法论啊,谢宁也是早期的摩托罗拉的工程师,之后自己单立独立的 咨询顾问之后啊,他总结出了一整套解决问题的方法,这里呢更多的用到了一些试验的方式,所以呢我们称之为谢宁 die 啊。 这里呢包括了像多变量技术,零部件搜索技术,成对比较技术,变量搜索技术啊等等等等。 这个呢可以认为是第四个流派或者叫分支啊,那目前呢?呃还有一个流派呢,目前还存在争议,但基本上大家也把他纳入了这个 due 的大家族,所以我们可以认为这是 due 的第五个流派啊, 叫蒙特卡罗仿真,就是我们现在的一些呃计算机或者是大数据的一些算法。他的提出者呢是,呃, 上世纪四十年代的这个冯诺伊曼,当时呢乌拉姆和冯诺伊曼呢是作为美国原子弹计划的呃,两位课题组的组长啊。之后呢,他们的呃 公布了一套算法啊,把他们当时的一些算法呢公布了一部分出来啊,那这个冯诺伊曼呢把这套算法呢?呃用这个美国的一个赌城 阿蒙德卡罗来命名啊,增加他的神秘色彩。呃,我们都知道就是你做这个原子弹啊,你不可能说好,我 呃排了十二次实验啊,我扔十二颗原子弹啊,所以呢一定是用很多的一些算法啊,最多扔上一颗两颗啊,然后呢呃去做模拟啊,所以更多的是仿真的算法,那这套呢叫蒙特卡罗,仿真名词本身呢是冯罗伊曼提出来的。那 当然呢,如果说我们要追溯这套方法呢,应该要追溯到一七七七年啊,到十八世纪了,那当时的一个数学家叫 bo 凤啊,他提出了这个呃,著名的一个头针实验啊,各位感兴趣呢,可以去百度啊, 他用这个头针实验的概率事件呢,来计算我们的圆周率判啊,当然呢,他不是 要精确到多少位,而是他这种方法本身啊,是创造了这个仿真模拟的一个鼻祖。 所以到这里我们稍微总结一下,我们的 d u e 呢,其实一共有呃五大流派啊,公认的是四大流派啊,其中第一个呢是经典 d u e, 代表人物呢是菲士尔啊,当然还有很多很多的学者的贡献啊,天后选一啊,等等啊。 第二个流派呢是呃,文件参数设计,也叫甜口 due, 代表人物呢就是甜口选一啊。 第三个流派呢是均匀实验设计法,代表人物呢是王源和方太太啊。第四个流派呢是现金实验设计法,代表人物就是先领。第五个流派呢是蒙特卡罗仿真, 代表人物呢,包括 boss, 乌拉姆、冯诺伊曼等等。 那我们为什么要去做实验呢啊?也就是说,一般来说呢,我们有三个重要的理由,一个是为了验证或者确定一个理论上的结论。 第二个呢,当对一个产品呢进行去研究。第三个呢,通过实验呢进行去确认,让我们得到高的质量或者是高的效率。 那实验的目的呢?啊,那我们做实验,那我们实验设计的目的呢, 就包括了以下这些方面,比如说提高产量了,改进质量,降低成本,缩短周期等等等等。而试验设计的目的呢,就是让试验更经济有效, 那我们试验设计的目的的分类呢?可以简单的,我们这块只是粗糙的分了三个方面,第一个呢叫描述变量的特征,第二个呢叫优化变量参数,第三个呢叫产品的一个参数设计描述变量的特征呢,就是去看 哎,我们的哪些呃自变量,就是我们的输入,我们这块也称之为 x 啊, 对于歪而歪呢,就是我们的输出,之前我们在讲试验的时候说过输入,哎,形象的比喻呢,是我们的手啊,那呃我们去改变这些 x, 然后呢对歪呢产生一些影响,进而来让歪呢发生变化啊, 所以呢,我们去判断哪些 x 就是我们的这个输入对于 y 输出影响 最大啊,这里呢当然包括可控的和不可控的 x 啊,最后呢,找到哪些是关键的 x, 进而呢去哎,需要仔细去控制。第二个呢目的呢就是优化变量参数,就是我们要去找到 x 和 y 的函数关系,让我们进而去寻找到我们 x 应该设定到多少,呃,应该呃调整为多少,竟然能够让 y 达到我们的要求啊,以及我们 x 和 y 各自的一个界限啊,规格线啊。第三个呢叫产品参数设计,就是说我们不仅要让 y 的呃能够达到我们的要求,而且我们希望我们的 y 呢啊, 他的波动尽可能的小,也就是他具备抗干扰的能力啊,就是我们的噪声因子,或者说我们的干扰啊,对他影响很小啊,那我们认为这是一个强健的设计,也叫稳健的设计 下来呢,我们跟大家介绍 do 一常用的一些术语,首先第一对术语呢,就是我们的 y 和 x, 指标和音词,那关于这个 y 啊,指标,那我们名称非常多,叫响应变量,也叫音变量啊, 也叫输入变,输出变亮骚扰,那我们另外一个呢,就是因此叫自变亮啊,也称之为,因此也称之为。呃,输入变亮。比如说我们这块呢,如果做一个焊接, 那我们焊接的温度啦,时间啦,这些都是我们的输入变量。这些呢,我们可以用手来改变啊,向使用 可以去改变它,直接去设定它。而我们的输出变量呢,比如说焊接的强度呢,焊接的产品的外观啦,哎,这个我们不能直接去设定改变,但是我们可以通过改变我们的输入,哎,让我们的强度啦,产品的外观啦,达到我们的要求啊。那我们这块呢,就跟大家介绍了一对名词 下来,这段名词呢叫做水平和处理啊,呃,水平呢,我们也叫 love, 处理呢,就是我们的一个组合,比如说我们有一个因子呢,叫温度,那我的温度呢,可以设定为两百度,这就是一个水平,也可以设为两百一十度,这就是第二个水平。
 08:36查看AI文稿AI文稿
08:36查看AI文稿AI文稿主要讲述一下部分实验设计中的混杂问题,也称为别名 j 题。是这样的,某工序过程有六个音字, a、 b、 c、 d、 e、 f 六个音词,工程师希望做部分音词试验,确定主要的影响因素,准备采用二的 六减二次方设计。这个学法是二的六减二, 而且工程师根据工程经验判定 abbcaeee 之间可能存在交互作用, 但 mini table 给出的生成员为一等于 abc, f 等于 bcd。 为了不让可能显著的二级交物相互混杂,下列生成员可行的是什么? 给出四个生成源,这里需要去了解的是 什么是生成员,然后什么是交互作用之间向互混杂 这两个概念如果了解的话,那么这一体就会变得非常容易。来看一下原设计是二的六侧方 减去二减去二,就相当于是两个生成员, 两个生成员就类似于一等于什么, f 等于什么这样的一个 结构。然后一等于 abc 是 什么意思呢?就是把 abc 这一列当成一的事业安排。 比如说最简单的有两个音子, a 和 b, 那么 a 和 b, 他有四次实验,负负正正负正负正。这四次实验,那么呢,还有一个 ab 交呼效应,他呢是正负负正。 我为了增加一个因子,假如说我增加一个 c, 那么我需要再增加一倍的实验,那我为了不增加一倍的实验,在这个实验上继续完成啊。三个因子的实验,那么就把 ab 等于 c 放进来, ab 等于 c, 如果放进来的话,那么这一列就变成了 c, 这就是 c 等于 ab 的 这样的一个生成员。那这个时候呢?你理解生成员是什么意思了?来这一题看一下他的解析。 首先说 abbcae 和 de 之间可能存在交互作用,也就这 四个, abbc 和 ae 一级第一之间是不能相等的,记住这个就可以了。然后呢,来看一下默认生成员, 一等于 abc, 然后 f 等于 bcd, 如果是这两个的话,来先找 ab, 第一个 ab 找出来,把两边同城上 c, 那这个时候呢,就是 ce 等于 ab, c e 等于 i b, 哎,看一看上面没有没,并没有那个 c e 这个选项,那 这个时候呢,有 ae 选项,来把 ae 两边同成一, aae 等于 bc, ok, 当 ae 等于 bc 的时候,那这两个是 产生了混杂,这两个产生混杂,这是不允许的,他们之间是不能有混杂的。所以从这里来看,原来的生成员是不能用了, 那么既然圆的生成圆不能用了,那他呢?给出几个新的生成圆。同样的方法,你可以在两边同时呈上一个字母的方式, 消去一个,然后生成一个,比如一等于 abd, 然后呢,两 边同时乘上 d, 两边同时乘上 d, 就相当于是 d e 等于 i b, 因为在这个概率里边,低称低的概率是等于一的啊,低称一低的概率是等于一的,也就是在低条件发生下,低的概率是多少?他是百分之百啊。在这个时候, d e 等于 i b, d e 等于 i b, 这两个是不允许出现的。同等方法,你可以计算 a, b 和 c 都不太适合。到最后你的选项只有 d 啊,你的选项只有 d。 在密集胎宝中如何指定生 成员?你可以在凉水瓶设计选择指定生成员,然后在设计中点生成员,把你所期望的生成员放入到这里就可以了, 生成员二二的六减二次方,同时可以指定两个生成员,但是呢,这种生成员可以有很多种,这两个可以有多种, 这个呢,你需要知道你设计的就是在设计这些东西啊,在实验设计呢,还有很多相关的内容,比如说筛选设计, 部分因子实验设计,全硬的实验设计等等,很多实验设计,实验设计相关的内容, 考试的时候大概会有二十分左右的分值,考实验设计,如果你的实验设计学好的话,在考试的时候你会非常的轻松自如,因为你这样想,二十分分布在一百二十分里面, 他呢会经常出现各种分值,对吧?经常出现,哎,突然间一个时间设计出来了,突然间一个时间设计出来了,如果说你的时间设计做的很顺,你就会一会一个简单的题,一会一个简单的题, 如果你的实验设计做的不好,那么你一会碰到一个男的,一会碰见一个男的,心情也不一样。好了,这一期的小胡 活动呢,是生成员在实际生产中他的作用是什么?你可以在评论区进行评论,也可以扫描左侧的二维码,加入到六七个码学习群里来。
42六堂课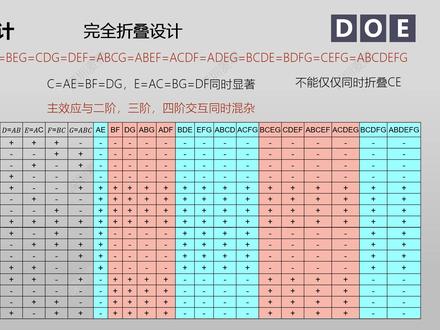 16:55查看AI文稿AI文稿
16:55查看AI文稿AI文稿嗨,大家好,今天继续介绍部分因子设计,包括筛选实验、饱和设计、折叠设计以及 p b 设计。 部分因子设计的主要用处是用于筛选实验。我们举一个例子,比如 p c b 版的翘曲, 经过分析,有七个潜在的因子水平是高低, 全因子的实验次数太多。一个选择是实施精度为三 n 的七减四设计,其后果就是主效应和二阶交互效应混杂, 节省时间、金钱和资源,当然是使用这个设计的主要原因。其他的还有,其一就是直接忽视二阶交互,其二就是实验结果有可能因此全部不显著。 其三是某些因子根本不可能交互,从而打破别名恋。 最后呢,就是实在不行还可以使用折叠设计, 分辨度为三的二的七点四设计, 有四轮减半,就有四个,生成员有十一个。广义交互实验次数从一百二十八次减少到八次, 七个,总自由度七个主效应,两者正好相等, 这种相等的情况称之为饱和设计。类似的分辨度为三的饱和设计,还有十五减十一以及三十一减二十六这种设计。 这种饱和设计有七减四, 等于三个基本设计 a、 b 和 c, 还有四个生成源软件提供,是 a、 b, d, a, c, e, b, c、 f 以及 a、 b, c、 g, 于是就得到 d、 e、 f 和 g。 然后是广义交互,两两相乘得到六个, 三三相乘得到四个,四个相乘得到一个,总共是十一个, 加上四个生成元以及 i, 就得到数值为十六的生成元组。 实验结果有八个。翘气值效应的帕雷多图显示 c 因子显著, 但是主效应 c 和 a、 e 以及 b、 f 两个二阶交互混杂。同时呢,工程分析不能排除 a、 e 和 b、 f 的交互可能,这就需要找出对策。 当前对策就是单因子的折叠设计, 由于是 c 显著,就用 c 乘以生成元组,得到与 c 混杂的 个别名结构组,将它放在这里,能够很好的帮助我们理解折叠设计。 折叠设计的操作方法是这样的,这是折叠前的部分因子设计 c 显著,但是 c 与右边的其余十五个交互混杂,就不能确定到底是谁干的。 现在增加八四实验,其他因子的水平不变, 只转变 c 因子的水平就是原来是负改为正,原来是正转变为负,这就叫做折叠单因子 c 的折叠。 于是有七个效应转变了水平,而其余八个不变。 于是当两个合并成一个设计并进行计算的时候,这个别名组的本来的十六个效应就被分成了两个别名组,相应的主效应和二阶交互效应就被分离了开来。 由于这时候所有的主效应和交互效应的对照系数之和都等于零,正交设计得到了保持。 为什么会这样?十六个相互 复混杂的效应乘以 c 等于负一后,含有 c 的都变了符号, 不包含 c 的没有变符号,而包含 c 的效应正好是别名结构组数量的一半,就是八个。 因为分辨度是三,所以二阶交互不可能包含 c, 于是就打破了 c 和二阶交互之间的别名链,然后生成了两个新的别名结构组, 这两个结构组对于显著的主效应 c 或者二阶交互分辨度变成了五 别名列就被打破,折叠实验达到了目的。 如果 c 和 e 同时显著,就需要完全折叠。设计, 不能仅仅同时折叠 c、 e。 我们来试一下,十六个别名组元乘以 c、 e, 只包含 c 或者 e 的就变了符号, 不包含 c 和 e, 或者同时包含 c、 e 的符号没变。 均匀分散的设计之下,这两种情况也肯定是各有八个,于是就分离成两组。 图示一下,原设计折叠 c、 e 就是同时变符号。 我们惊喜的发现,主效应 c 和二阶效应继续混杂,主效应 e 也是如此,地方有限就没有展示,这实在是折叠了个寂寞。 这种情况只能完全折叠,就是折叠所有因子。 将别名组乘以 a、 b、 c、 d、 e、 f、 g 接数为基数的,没有变符号,偶 口述的变了符号,于是打破了主效应和二阶交互的别名列。如图所示,主效应和三阶交互混杂。 分辨度为四的设计也常用于筛选实验,当然有时也会需要折叠设计。举例二的六减二设计, 这是构建出来的,设计有两个生成员软件提供,是 a、 b、 c、 d 和 b、 c、 d、 f。 广义交互就是 a、 d、 e、 f 合在一起生成生成元组。这个设计二阶交互相互混杂,比如说 a、 b 等于 c、 e 显著,同时无法通过工程分析打破别名链,就需要折叠。 需要注意的是,分辨度为四是没有完全折叠的。 来看看为什么这是折叠前第一个别名组是二阶交互滚砸, 第二个别名组是主效应和三阶交互混杂。现在完 完全折叠,也就是 a、 b、 c、 d、 e、 f 都更换符号,可以看到,二阶交互的别民组没有任何改变,只是顺序发生变化而已。 主效应和三阶交互的别名组也是如此。这是因为分辨度为四的设计,偶数字母数的效应相互混杂,基数字母数的效应相互混杂。 全部折叠会覆盖所有的字母,大家要么同时变符号,要么同时不变。 分辨度为四, 只能单因子折叠。比如说折叠 c, 拿出一组包含 c 的别名组,乘以 c, 然后 a, b 不变,符号 c, e 变了符号,这个别名组裂变成了两个新的别名组,分辨度来到了六,于是二阶交互的别名链被打破了, 但不包含 c 的别名组,其二阶交互的混杂依旧。 顺便说一句,大家参看 metip 提供的别名链,包含任意字母的有五组,不包含的有两组, 所以说折叠一个基本就能解决问题了。这是设计图,表图是折叠 c 后,右边的两个别名组被拆分为四组。 看完前面的折叠设计,我们知道折叠设计的第一步就是用有限的次数设计一个低分辨度的实验。 第二步是根据需要增加相同数量的实验进行折叠,用于分离混杂。 这种多次实验可以合在一起。前面的实验数据机器使用的 方法叫做蓄贯实验,在 d o e 实验设计中经常用到,目的就是节省资源。 饱和正焦筛选实验虽然好,但是能够提供的设计太少。 p b 设计是一个补充, 它的实验次数只比因子数量多一个。与饱和设计一样, 水平数也是二,但是 n 是四的倍数为十二、二十二、十四、二十八、三十六等。如果是八十六和三十二就是因子设计, 相应的 k 就等于十一、十九、二十三、二十七和三十五等。因子设计被称为几何设计, p b 设计就是非几何设计,因为 n 不是二的整数次方。 总结下来, p b 设计就是非几何。饱和设计,只关注主效应,根本不考虑交互效应。 在 n 不等于二十八的时候,根据 n 的不同, p b 设计根据这样的高低水平顺序来展开构建。我们就用 n 等于十二 二的例子来看看构建的过程。 实验次数等于十二, a 因子的前十一次实验的水平选择按照上面的顺序, b 的十一次是将 a 的复制过来,然后整体向下移动一个位置, 再讲最下面的移到最上面,剩余的九个因子也是如此操作。 第十二次实验都选择低水平,这样就完成了设计。构建实验之后 得到十二个响应值,这里的主效应的系数之和等于零,可以计算他。尽管主效应与很多二阶或者高阶部分混杂。 p b 设计眼不见心不烦,只关注主效应, 它的对照效应。平方和的计算与因子设计为同, 这是计算出来的对照效应和平方和,大家可以自己试一下, 这是效应,帕雷多图显示没有因子显著。 当 n 等于二十八时, p b 设计是这个样子。 总结一下, p b 设计用于筛选实验次数, n 是四的倍数, n 的数值不同,高低水平的排序不同, 其交互效应的别名列十分复杂,只关注主效应,忽视交互效应。 最后计算方法与因子设计基本相同。 最后是超饱和设计,饱和设计的因子数量 k 等于 n 减一,如果 k 大于 n 减一,就需要超饱和设计。这里就不展开讨论了,这次的视频就到这里,谢谢观看,下次再见。
44深圳麦粮












