如何在ppt中呈现动态单页双曲线
粉丝1239获赞1567
相关视频
 42:25
42:25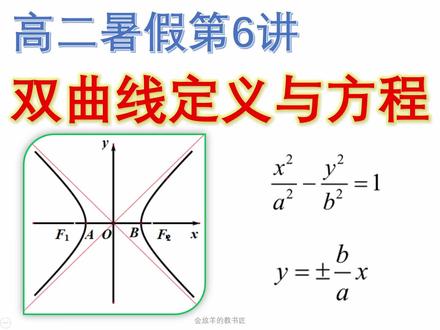 23:24查看AI文稿AI文稿
23:24查看AI文稿AI文稿大家好,今天我们继续来讲双曲线的定义与方程。上帝课讲的是椭圆的定义与方程,这两者之间还是联系挺紧密的。我们先来看双曲线的定义。什么叫双曲线呢?先读一下平面上到两个定点距离之差的绝对值等于长数,这样的动点的轨迹呢,就叫做双曲线。 其中这两个定点也就是图中的 f 一和 f 二,这两个定点呢,就叫做双曲线的焦点,然后两个焦点之间距离仍然是叫做焦距。双线的焦距, 那么什么意思?这样说,点屁是平面的一个动点,但是这个动点他不是随便去动的,他在动的过程中必须得保证。你看, 在我们图中这样一个点, p, 你必须得保证肯定是 p f 一更长一些,长的减去短的 p f 二。就这两个距离相点之后啊,它是等于一个长数,我们把这个 常数呢,即为二 a, 然后这个 a 是一个确定的数字,而且他必须较小于这个 f e f 二。其实交际的话,我们仍然是用二四来表示的, a 小于 ca 呢,是跟双曲线有关的基本量, c 也是跟双曲线有关的基本量,就这样一个意思了。 好,那只要满足了 pf 一,减去 pf 二,他距离之差等于一个长寿。那此时点批的那种轨迹就是双曲线的右直了。你注意啊,我说的是双曲线的右直。双曲线,双曲线肯定是有两只的,开口向左向右,那还有左只啊,左只的话其实也好理解,我写一个 p 一点吧, 显然 p 一点肯定跟这个 f 二的距离更长一些, p 一点跟 f 一的距离呢,更短一些,所以说应该是 p f 二 p 一 f 二,然后再减去图中的我画的这个 p 一 f 一,然后 他这个距离之差也必须等于同样的长寿,他也是小于 fef 二之间的距离的。我们一般来说,焦距也是用二次来表示,没问题吧?那么点 p 可以在左之上,也可以在右之上,也就是说 pfe 和 pf 二不一定哪个长哪个短,所以这个时候怎么办呢? 你把两周统一一下,我们只需要 p f 一减去 p f 二,加个绝对号,让它等于二 a, 然后这个长数小于 f r f 二之间,这样的交举二 c 不就可以了吗?这个就是双拳的定义了。 那么现在的话,我们要研究一下什么呢?要研究一下这个位置,这个小鱼,嗯,小鱼的话肯定就是双据线,那如果等于呢?也就是说 p f 一减去 p f 二,如果说它正好等于 f e f 二 距离,那此时点屁的轨迹究竟是什么呢?此时我想说的是,你看啊,点屁肯定是在 f e f 二点上,线上看我画的这个屁片啊, 这没问题吧?这个就是 pf 一,是吧?然后我画的这个,这个就是 pf 二吧, pf 一减去 pf 二,也就是说此时 fef 二和点 p 是贡献的,我们应该说的是此时动点点 p, 它是在 f 一 f 二延长线上, 也就是说点 p 的轨轨迹呢?他是一条射线 f 二,网友,他是一条射线,所以就不是双据线了啊。第二种情况,你说 p f e 减去 p f 二,有没有可能是大于 f e f 二?不可能,此时这样的点 p 是肯定都不存在的,在任何一个地方都不存在, 应该明白这样的意思吧,你可以研究一下。再说了,三角形的三边关系也告诉你了,两边之差必须小于第三边才能构成三角形吧。 两边之和必须大于第三边才能构成三角形吧,你怎么可能两边之上的大于呢?反了啊,应该是小于号的。好,继续来看第二点,那既然有了双曲线的定义的话,我们就根据双曲线的定义来推出双曲线的标准方程。什么叫双曲线的标准方程?其实很明显,我们看右边这个图, 也就是说焦点呢,一个是在 x 出版轴上,另外一个是在 x 正版轴上,并且 f e、 f r 这两个焦点,它是关于圆点对称的,那此时就是标准位置。当然你开口向上向下,也就是说焦点在 外轴上行不行呢?这个是 f 二,这个是 f 一, f e f 二肯定关于原理对称也可以啊,开口向上向下,或者开口向左向右,这样的双曲线呢,都是标准位置的双曲线。注意,我们求的双线的方程是双曲线的标准位置的方程啊,简称双曲线的标准方程。那么怎么来求呢? 因为 f 一 f 二,我们一般来说就是用二 c 来表示焦距点,所以 f 一点的坐标好记吧,肯定是记为负 c 的号令,那么 f 二的坐标肯定是正 c 的号令,这也是两个定点。那好,继续来看, 我们现在求的是动点点屁的轨迹,求出来呢是双据线,那么你既然求的是动点点屁的轨迹,所以假设点屁的左边就是 xy 了,看一下最终这个 xy 满足什么样的条件,什么样的方程 来根据双线的定义可以得出来吧。那你去掉绝对号之后的话,其实也就是绝对号里头这个 pf 一 减去 p f 二,不一定哪个长那个短啊,所以应该是等于正负二 a, 你看这个位置就是正负二 a, 那么接下来根据两点之间的距离攻势点 p 到 f 一的距离,是不是啊?横走八减,横走不要扣这个平方,然后外减零扣这个平方。开根号 这个部分呢,就是 pfb 的长度,那另外一部分他就是 pf 二的长度,那就是转换成两点零距离公式了。那接下来的话,这个方程我想说的是啊,他肯定代表双曲线的方程,但他不是双曲线的标准方程,他的样子太丑陋了, 而且看起来非常不舒服的疑点是什么?他有根号吧?求解啊,运算都不方便,所以我们考虑是把根号去掉。 如何把这个根号去掉呢?跟上集和讲的椭圆球椭圆的标准方程步骤是比较类似的,你第一步不能说左边平方,然后右边平方,这样就是错的,最终求出来的是指会出现四次方,特别的复杂。怎么办呢?我们考虑这么来处理啊,也就是说 根号下 x 加 c, 这样吧,根号下 x 减 c, 我们移到等号的右边,嗯, 然后就变成加号了,然后原来就有个征服而已,然后左边的话,我们就只保留原来的这个 x 加 c 控制的平方,加上外方,接下来我们左两边再平方就没问题。左边平方的话,我直接把括号打开,是 x 方, c 方外方肯定都有,然后还有一个二 cx, 然后右边的话也是平方啊,他平方的话,把括号打开,就是 x 方, c 方外方都有,然后再减去二 cx。 嗯,后边呢,有一个正负二一的平方,那就是四 a 方, 但是还有一个交叉项目,就是正负四 a 乘更好。想我里头首先再写一遍,把 x 减 c 的平方,然后外的平方显示这个样子之后的话,有些地方还是挺开心的,比如说画横线部分等话,左右两边一致吧,那你是不是左右两边画横线的部分都可以削掉呢?就 x 方、 c 方和外方 都消掉了,那么消掉之后的话,你注意左边有个正的,右边有个副的二 cx, 那都移过来,就变成了四 cx。 首先我把这个四 a 方也移到左边来,就变成了减四 a 方,然后等于四 a 根号下, 然后 x 减 c 控制的平方,再加上外的平方变成他了。变成这个样子之后的话,首先你要化减的话,左右两边可以乘一个四分之一,或者除四,都一样啊,我们把这个四都消掉了, 好,就变成这个结果了吧,这个结果就非常接近最后那个结果了。你的最终目的就是想把所有的二次根号都去掉。怎样去掉这个根号啊?对于圈里这个狮子来说,继续平方就行, 接下来的过程就不是太难了。平方之后啊,就这个狮子平方之后,最终就得出来这样一个结果了,得完这个结果之后的话,形式上还是挺对称的,对不对?嗯,挺美观的,但他仍然 不是商界的标准方程。我们要注意的是这个二 a 啊,他是跟商界线有关的基本量,这个二 c 呢,是焦距,他也是跟商界线有关的基本量。那么既然说这个 a 是小于 c 的二, a 小于二 c 呢? a 小于 c 的话,我 c 的平方减去 a 的平方,它的减小的等于 b 的平方,没问题吧?我引出来一个新的基本量,也就是说最终引出来的 b 呢,也是双线的一个基本量。 好,只要这么引的话,那后边就简单了,我只需要把这个位置写成 b 的平方,括号里头四方线减 a 方便成 b 的平方。其实呢,这个方程很快就可以变成这样一个结果了,也就是说 b 方 x 方减去 a 方,外方等于 a 方 b 方,接下来左右两边同处, a 方 b 方就变成了 a 方分至 x 方, b 方分至外方,等于一变成了这样一个形式。 变成这个结果的话,我想说的是这个结果他就是双曲线的标准方程,当然详细一点说的话,应该说的是焦点在 x 轴上的双曲线的标准方程。 那么现在你肯定有疑问了,老师,我求出来之后的话,那焦点在外轴上的双线房产怎么办?那你交换一下 x 和外的位置不就可以了吗?所以接下来看好了吧,这个就是焦点在外上的 外轴上的这样的双键的标准方法就求出来。注意 a 和 b 之间没有绝对的大小关系,因为我们只需要保证 a 方加 b 方等于半焦距的平方,等于小四的平方就可以, 所以 a 和 b 呢,两个数字都大于零就可以了。那接下来我们就要介绍一下究竟这个小 a 小 b 他代表商店的什么几何含义。来看图继续来看了啊,这个表格其实说的还是挺清楚的,但是有些小细节需要改一下,哪呢?我们以焦点在 在 x 轴上的双线为例,我们先来看外的范围啊,还有 x 范外的范围很好说,因为你上下是无限延伸的这样的双下,所以说外的范围是取实数就行,但是 x 的话也不是啊,显然对于组织来说, a 点是最右端的点, 对于幼稚来说, b 点是最左端的点,也就是说点 a 和点 b 是双线的,两只跟 x 轴的交点。 a 点坐标很好求,因为你 你这个动作包是零对吧?你把 y 等于零带到这个里头,那就变成了 x 方等于 a 方,也就是说 x 算出来两个指,这个 x 呢是正负 a, a 点位于副板桌上,他的坐标就是负 a, 然后 b 点坐标呢,是正 a 多少零?哦,原来是这么个意思啊,求安这个 a 点 b 点之后的话,你注意 a 点 b 点,他是在双曲线上的,我们求的是双曲线上所有的点,他这个 x 和 y 的范围,所以呢,这个位置是不是 应该写上方括号啊?也就是说, x 的范围是可以取到这个负 a 和正 a 的 x 真正的范围应该是负无穷到负 a 的左开右 b, 然后正 a 到正无穷的左 b o 开,应该这么写,包括缺点在外头呢情况你自己也可以讨论一下,必须是这样的方括号才可以明白吧,稍微改一下就行了。 那好,继续来介绍啊。继续来介绍的话,我先介绍什么呢?你暂时认为这个小 a 和小 b 就是跟双曲线有关的基本量就行。我们先用小 a 和小 b 求一下双曲线的什么东西啊? 求一下。双曲线的渐进线,少一个字啊,什么叫渐进线呢?其实这个名字大家应该不陌生的啊,初中的时候我们学过双曲线的外等 x 分之一,凡比利行说的图像是双曲线,只不过初中的时候呢,这个双曲线它不是放在标准位置,它这个图像是位于一三两个 将线的。有没有鉴定线啊,告诉我这样一个防比例还是录像有。这个双线的鉴定线是 x 轴和外轴,你看鉴定线,鉴定线必然是两条吧。那么怎么去求双线的鉴定线呢?来看这一页,然后原来鉴定线是这么,那么这个鉴定线怎么得出来的,你记住就行了啊,是这样得的, 鉴定线,鉴定线直线都是 y 和 x 的依次是吧?那好说,我这个位置只需要写成 xb 上 a 的依次方, 然后这个位置呢,只需要写成 y 笔上 b 的依次放,因为窗。嗯,他这个双线是有两条,这两条双线的间接线, 这两条生命线的间接线的话,肯定是关于什么关于 xo 对称的,所以我加上正符号这两个字,等号右边变成零就行了,求法,你记住就行。其实另外一种写法的话,你就完全可以写成外等于正 正负 a 分之 bs, 这么写也是没有问题的,这就是双线的间接线,那么焦点在外轴上也可以这么记啊,方法一样的,你看这个是焦点在外轴上的这样的双线的标准方程吧,既然焦点在外轴上的话,它的间间线也可以外比上 a 的一次放,中间变成了加减号啊, 然后呢, x 比上 b 的依次放等于零,那最终他就是 y 等于多少?正负 b 分之一 x, 这就是间接线。那么有了这两条间接线之后的话,我可以标的更清楚一些。咱们以焦点在 x 上为例, 外等于 a 分之比 x 没问题吧?外等于负的 a 分之比 x 也没问题吧?因为一个往上走,一个往下走,它的斜率正好是互为相反数的好。有了间接性之后的话,接下来我们就可以看这个 abc 它的实际含义是什么了。小 c 的话其实是最容易的,这个二 二 c 就是图中两个焦点之间的距离,所以说二 c 叫什么名字啊?二 c 的名字,或者说几何亿,对于双曲线来说,他就叫焦距,那你说这个小 c 叫什么,他当然就叫半个焦距了啊,简称半焦距。好,这个是没有什么问题的。 那么这个二 a, 我们先看这个二 a, 二 a 究竟代表什么呀?好说,看左边这个图之前我们已经求过了,左端点和右端点,这是实实在在存在的两个点,然后 a 点坐标是负 a 的,后面 b 点坐标呢?是正 a 的话,量已经求过了。所以 ab 这两个端点连线,它的长度呢,正好是等于二 a 的,它是实实在在的存在的。我想说 ab 有一个名字,它是什么名字啊?它是十轴, ab 的名字就叫十轴,所以二 a 这个名字叫什么?叫十轴长,那小 a 这个名 名字当然叫半时轴长了,或者叫半时轴都行啊,半时轴长好, a 是叫他,那 b 叫什么?我先说名字,再告诉你这个 b 是怎么出来的啊?二 b 呢?他的名字对于双线来说,他叫又十轴,就有虚轴,咱们中国人起名字还是非常好的啊,叫虚轴长, 那 b 的话叫什么? b 的话当然就叫半虚轴了,或者说就叫半虚轴,长度就可以啊,就这样一个名字,这就是他的实际含义了,实际的结合含义。 那么为什么他叫虚荣呢?实则我理解实实在在的存在。那好说,看好了啊,我们过 a 点 b 点分别做 x 轴的垂线。看到了啊,做 x 垂线,因为它是高度对称的呀, y 等于 a 分之 b, x 下边这个鉴定也是 y 等于负的, a 分之 b x。 我们做了这两条垂线之后 么?分别跟谁相交啊?跟这两条尖尖线相交,比如说左边交于 mn 这两个点,右边交于 pq 这两个点,那么 mpq 的坐标肯定都能求出来吧。比如说我求一下啊,看 mn 的坐标,这个 m 点的坐标的话,横坐标肯定是弗雷拉跟一点一样, 然后纵坐标的话,你把负 a 带入到这样一个间接线的解决室里头,那不就是分成了负 b 吗?那 n 点的话,就是负 a 多少正比,所以说 m n 的长度等于多少啊,我们把这个举行连起来哦,举行连起来之后的话,原来图中他这个 m n 的长度 就叫轴多少呢,就叫做二 b。 实际上你可以完全把这个 mn 呢移到哪?移到外轴上,其实 mn 外轴上这个 mn 他就叫虚轴了,能明白这个意思吧?为什么他叫实轴呢?因为 ab 这条轴是实实在在存在的, 为什么他叫虚轴呢?虚轴只有我们构造了这样一个辅助举行之后,才能够得出来这个二 b, 所以一个叫实轴,一个叫虚轴,然后小 a、 小 b 的名字分别叫半世轴和半虚轴。小 c 的话好理解,就是关焦距了。 注意,在双圈里投达这个 abc 之间的关系是必须满足这三个正数, c 方等于 a 方加 b 方才可以。现在已经解释清楚了吧?那我们继续来往后看离心率啊, 跟椭圆类似的,他这个双圈也有离心率,只不过呢,椭圆的离心率是小于一的,在零到一之间。 嗯,然后对于这个双线来说,双线的离心率肯定是多少大于一的呀?为什么?因为 c 方等于 a 方加 b 方, c 是最大点在 abc 里头啊, a 分的 c 肯定是大于一的。那么现在我想得出来的一个结论就是,对于离心率来说啊, 离心率和双线开口大小有什么关系呢?我们可以仍然观察一下这个图,渐进线,那就标上吧。什么叫开口啊?其实你这个渐进线,渐进线,渐进线这个夹角,这个 c 的 越大,那此时他这个双拳的开口就越大,是吧?那实际上不就是说你这个斜率是等于贪正的 ct 没问题吧?这个贪正的 c 的越大, a 分之 b 越大,开口就越大。那我懂了,也就是说 a 分之 b 越大, 开口就越大吧。同样的, a 分之 b 越大,中间这是个加号啊, e 就越大。所以我们应该写的一个结论是什么呢?首先对于离心率来说,你应该注意的是他是大于一的常数。第二点,离心率越大,双对性的开口就越大,离心力越小,双对性的开口, 我就越想,你应该这么去认为才可以明白吧。那最后来看通镜,什么叫通镜呢?通镜的话咱们还是写上他的定义吧,过 f 一或者你过 f 二也行啊,做这个 mn, 他必须是垂直于这个,谁呢?垂直于这个 x 轴的, 或者说垂直于十轴的 pq, 那么通电的定义就是垂直于十轴的,那焦点在 x 上,十轴不就是 x 轴吗?啊?十轴所在的直线垂直于十轴的焦点弦。 其实弦的话还是挺好理解的,什么叫弦啊?任意连接双圈上任何两个点,比如说看右边这个图,你说这个 ab 叫不叫弦?叫弦,这个叫两只弦。哎,你说此时这个 ab 叫不叫?这也叫弦,叫一字弦。为什么叫一字弦单只弦呢?因为它 a b 这两个点在双线的同一之上啊。你如果刚才这种情况, a 点和 b 点在双线不同的两只上的话,那就是两只弦,两只弦和单只弦或者双只弦,单只弦知道名就行。那什么叫焦点弦呢?焦点弦就是过焦点的弦啊,你看过 f 一 哎,这个 ab 是不是就焦点弦啊?因为 ab 这条弦他是过焦点的,这就叫焦点弦啊,处于之于十者的焦点弦。 最终呢?不管是 pq 还是说左边这个徒弟 mn, 他都叫做通镜。那 mn 的长度怎么求?很好求。首先 m 点的横坐标跟 f 点坐标都是负 cn 点,同样的也是负 c, 那 m 点和 n 点他这个动作表怎么求啊?我们只需要把什么把标准方程里头这样一个横坐标变成什么 a 分之 a 方分之 c 啊,懂了,把这个 x 变成 负 c 就可以了,然后再减去 b 方外方等于一,然后经过整理以后,这个方程呢,最终会得出来这样一个结果,外方是等于什么点?等于 a 方分之 b 的四次方,那再继续来求的话,那外不就是正负 a 分之 b 方嘛,那 m 点是在 x 轴以下,所以就是负的 a 分之 b 方。 n 点在 x 轴以上,那就是正的 a 分之 b 方。 所以说通镜挨门的长度,最终求出来不就是 a 分之二 b 方了?这个在大题小题里,通镜这个公式啊,这个 a 分之二 b 方都是可以直接用的,小 a 小 b 就是我们之前讲过的双选的其中一个基本量很清楚了吧。那接下来还是要练题的,先来看第一道题啊。 第一道题,首先你需要把它画成双圈的标准方程的形式,我们外方比上一减去 x 方 乘二,不就是除二分之一的意思啊,也就是说此时这个 a 方就是一,然后 b 方呢,就是二分之一,他这个焦点还是在外轴上的,对吧?嗯,焦点还是在外轴上的,然后焦点在外轴上的话,他这个四方就是等于一,再上二分之一,等于二分之三吧。所以我们这个 abc 都可以求出来, b 是二分之根号二, c 是二分之根号六,是吧?啊,然后这个离心率的话呢,就是 a 分之 c 也等于二分之根号六。然后继续来求一下别的啊,十周虚轴这个顶点坐标的话,你就自己来求一下就行了。然后离心率,嗯,通镜呢? 通键呢?通键的话你就记住就行了。 a 分之二 b 方啊,通键的长度它是等于一分之二乘二分之啊,奏出来是一啊,然后间内线呢?间内线的话,一定记住是两 调吧,那怎么来求呢?外方比上一的平方,那不就是外比上一,然后再加减,然后这个 x 比上谁啊? x 比上二分之一开杠,那就是二分之跟上二, 那等号右边应该画成零,那最终的话,他这个间接的方程,我们写成外等于正负根号二位的 x 就行了,这就是间接方程有两条问题了吗?所以说解这种问题的时候呢,我们只需要先把它画成 标准方程,然后观察一下焦点在 x 之外之上就可以。包括第二题的话,也是你首先应该改成外方比上二分之三,然后减去 x 方,比上四分之三等于一, 二分之三不就是 a 方吗?那 a 的话就是二分之根号,六开根号,然后这个 b 方不就是四分之三啊,所以说这个 b 的话,他就是等于二分之根号,三开根号, 然后这个四方的话,他俩加起来其实是一个四分之九,所以说小 c 就是二分之三了,都是开根号就行。那剩下的这些量将近线啊,离心率啊,通径啊,你自己来求应该是没问题了吧。那我们继续来看第二题啊,第二的话,我其实我更加建议你先做第二题,第三题,为什么呢?马上你就知道了, 他已经给了你这样一个方程,焦点是在 x 轴上的,焦点在 x 轴上的双据线的话,我首先必须得满足这两个分母,怎么样?这两个分母都是正主吧, a 方 b 方肯定都得大于零了, 所以说那个 a 方是谁? a 方不就是二 k 减五啊,在这道题里头得大于零,那那个 b 方呢?那不也是 k 的绝对值减二的大于零吗?那最终求出来一个就是 k 大于二分之五,另外一个呢,就是 k 的绝对值大于二,那就是服务穷到富二, 再并上正二和中不穷的意思。两个是且的关系啊,就是说这两个分不得同时都得 怎么样都得大于零岁,且的话就是这两个范围,我们最终求这个交集就行了。求交集的话,那不就是二分之五投政务球吗?没有问题啊。那继续来看第三个,其实第三个的话也差不多,第三个的话焦点在外轴上。 嗯,这样你只需要保证画圈部分这两个分母都是复数就行。比如说随便举一个例子, s 方比上负一 减去 wifi 上,外方比上个负二吧。我随便举了一个例子啊,那整理之后的话,实际上他就相当于这个外方比上正二,再减去 x 方比上正一。你 说焦点是不是在外出上?是,所以说这就给我们领导了,我只需要保证,嗯,画圈部分这两个分母都是负数就行。好,也就是说二可以减五 得是负数啊,小于零。并且呢,这个 k 的绝对值减二是负数也得小于零。那最后求完了之后,就是 k 小于二分之五,并且得满足 k 在什么方面的呀?在负二到正二之间,两个球交题,那最终靠三答案就出来了吧。负二到正二之间。 你要注意,他给的这样一个方程本来就是双线的标准方程,要么是在 x 轴上,焦点要么是焦点在外轴上。所以呢,两种情况综合起来,那不就是双线的意思吗?因为括号一他并没有说焦点必须在 x 轴还是外轴上,所以呢, 科二的情况还有跨三的情况,一综合就行了。所以你现在知道为什么要先做二和三了吧,综合一下并起来啊,负二到正二,再并上二分之五到中五九。好了,这道题就讲完了,分享课堂知识,感受数学之美。我是杨帆老师,下节课再见。
8237会放羊的教书匠 00:13
00:13














