人教A版必修二立体几何158页
粉丝10.4万获赞49.2万
相关视频
 17:40
17:40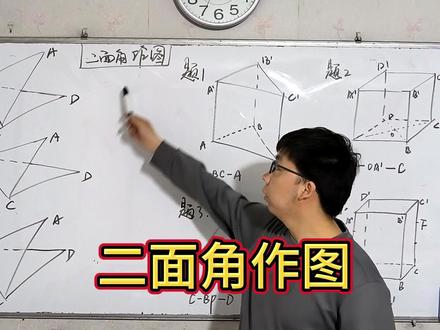 10:37
10:37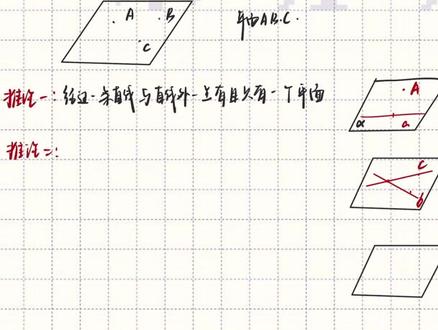 08:55查看AI文稿AI文稿
08:55查看AI文稿AI文稿大家好,我是末班班长。那因为很多同学想听一听几何与概率这方面的课程,所以为了平均一下进度,那我们就从八点四开始继续这个课程,然后之后再把前面落下的补齐, 那因为八点四是第八章的这一部分的重点。哎,前面的内容基本上我们可以把它归结为画画课和我们的记忆课,主要是记一些公式。 哎呦,顶点棱,平面多边形构成的棱柱跟棱锥来得到相应的结构特征,这部分就是要进一步研究,我们看这个顶点我们是可以把它看成是点的, 棱柱我们可以把它跟直线相关,而平面多边形他跟平面相关,所以我们八点四开始就要进一步的研究点直线平面之间的位置关系,那么这一节我们将从平面入手。那第 一点,平面什么是平面呢?我们初中对于点与直线的认识是由于一些现实事物中抽象而来的,那生活中有哪些跟平面是相关的呢? 比如说我们的课桌,比如说我们的黑板以及窗户,我们可以把它看成是数值的平面,那通过把这些事物抽象出来,我们就能够得到几何的平面,那这一部分我们只要去理解平面的意义就行。如果我们说直线 是可以向两侧无线延伸的,那么平面他就是可以向四周无限延展的, 当然这里表示的都是无线哦,那我们在表示直线的时候,我们只需要画出直线的一部分就可以表示整个的直线了,所以在表示平面的时候,我们也 可以只画出平面的一部分来表示整个平面,那怎么去画呢?我们会用一个平行四边形来表示,像这样的一个平行四边形,他就很像我们水平的一个平面。那怎么去画竖式的平面呢?就是把它竖过来,把它竖过来的话,我们经常画的其实是这个方向的,哎,是不是很像切进来的一个 一个平面呀?好,大概是这个样子的,那我们也可以去画出斜的,哎,这个样子就是一个斜的平面,那我们会用希腊字母来表示平面,我们把它会写到这个平面的一个角里面,阿尔法呀,贝塔呀,伽马, 那我们可以把他们称为平面阿尔法平面贝塔跟平面伽马,哎。或者如果你把这个四边形他的端点写出字母 abcd, 我们也可以把 它叫做平面 abcd, 哎,这样子都是可以的。那平面有什么样的性质呢?我们经常说一句话叫做点动成线,线动成面,说明两个点动嘛,你得有之前的点跟之后的点,这样两个点会确定一条直线, 那线动成面的话,那你肯定也要有之前的直线跟之后的直线,他是能运动过来的,这样的两条线构成一个平面。同学们想想看,你要想两条线的话,至少我们需要几个点呢?至少我们是需要三个点的, 所以也就说明三个点就能够构成一个平面,但是是有要求的,我们这个线你得表示之前运动之前跟运动之后的呀,所以这两条线他一定不是同一条直线, 所以说明这三个点他一定不在同一条直线上,不在同一直线。两 两条线指的是运动前跟运动后的,并不是两条直线确定同一平面,哦,因为两条直线,尤其在空间里,他不一定是在同一平面之内的。你要记住的是三个点确定的 直线,那我们得到了第一个基本事实,我们说过不在同一直线上的三个点,哎,确定一个平面,尤其 只有一个平面,哎,我们也可以把它简单的记为不贡献的三点确定一个平面,那如果我们将这三个点记做 abc, 我们这里简单画一个平行四边形,哦,如果我们把这三个点 abc, 那么这个平面也可以称作平面 abc, 那我们又知道三个点确定一个平面的话,但是两个点就能够确定一条直线了。那也就说明,如果我们有一 一条直线,然后再加一个点,那也是能够确定一个平面的,哎,如果我们有一条直线,这个直线是 a 直线,然后有一个 a 点,但是你一定要说明清楚,这个点是在直线外的一点,那这样我们就得到了第一个小推论。 推论一,经过一条直线,哎,这表明的是 a 直线与另外一个点与直线外的一点,有且只有一个平面。好,这是第一个小推论,那两点确定了一条直线, 那么这两个点也同样能够确定一条直线。那同学们看, b 直线跟 c 直线,他是相交的两条直线,这也就说明经过两条相交直线,有且只有一个平面。推论二,经过 两条香蕉直线油且只有一个平面,那我们再 接着看,那这两条直线他也有可能,哎,我们一、二、三,还是这三个点,哦,有可能这里有一条直线,哎,那我不相交的话,我也可以平行啊,我过这一点做与你平行的直线,哎,这有什么不可以的呢?对吧?所以经过两条平行的直线, 平行,直线也是有且只有一个平面。好,这是我们基本事实。一,那我们接着想,我们说直线呢,它是由无数个点构成的,而平面是由无数条直线构成的, 那直线又由无数的点构成,说明我们直线与平面他们都可以看成点的集合,那这个点就是构成这两个集合的元素。如果我们说点 a 在直线 l 上的话,如果我们想表示这不就相当于元素在结合之内吗?我们就可以把它记为这个点 a, 它是属于 l 的, 这样子写就是可以的。那如果点 b, 它在 ly, 这个 l 表示的是直线哦,如果点 b 在 ly 的话,我们就可以把它记为 b, 是不属于直线 l 的,那同样平面也是点构成的集合。所以如果是点 a 在平面阿尔法内的话,我们就可以把它记为 a, 是属于阿尔法的,那如果我们有点 p, 它在阿尔法外的话,我们就可以把它记为 p, 点是不属于阿尔法的,那我们接着思考一个问题,那平面与直线的关系,我们是不是能够通过点的个数来确定呢?你说如果如果有一条直线,这个直线有两个点, 而这两个点他就在我们的平面内,在一个平面内,那请问这个直线与平面什么关系啊?你要是有两个点的话,那已经确定了,你整个这条直线 都会在这个平面内,所以我们就能说明这条直线,这条直线就在这个平面内,平面内这是我们的基本四十二, 那这个时候我们直线在平面内怎么表示呢?我们刚刚也说直线跟平面都属于点的结合,那现在我们表示的就是结合与结合之间的关系,结合与结合之间怎么表示啊? 哎,我们得用包含,所以在平面内的话,我们就可以把它写为,这里需要有两个点,既在直线上,又在平面上,那就是点 a, 它是属于直线的,点 b 也是属于直线的, 并且这两个点还都在平面内,属于阿尔法的 b 也属于阿尔法则,我们 l 他就会包含于阿尔法。好,这是我们关于基本事是二,那我们接着思考一个问, 如果我们这里有一个书桌,那这里我们拿一个三角板。好,这是一个三角板,我们把他这个顶点就抵在书桌上,这个三角板他跟桌面这个平面是有一个焦点的,这就是他的公共点。那请问这个三角板所在的平面跟我们课桌这个平面有什么关系呢? 那我们把这个平面补齐。好,我们把这个平面补齐了。那正常我们在画平面的时候是要把遮挡部分都换成虚线的,我在这里把这个遮挡的地方擦一擦, 这里也是一个虚线。那我们看这个阿尔法平面跟贝塔平面他们两个平面是相交的,那我们说直线跟直线相交会相交于一点,那么平面跟平面相交就会相交于一条直线。 那么如果你这两个平面他不是重合的话,只要有一个公共点,就说明这两个平面是相交的,只要相交就会有一个 公共的这个胶线,而且这个胶线他是一定会通过我们原来的公共点的,那这样我们就得到了基本四十三,如果我们有两个不重合的平面,不重合的 平面,哎,如果有两个不重合的平面,他们有一个公共点的话,那么一定有且只有一条 过该点的公共直线。好,那这就是我们第一节的内容,包括什么是平面以及三个基本事实,希望大家好好理解。
2542数学末班班长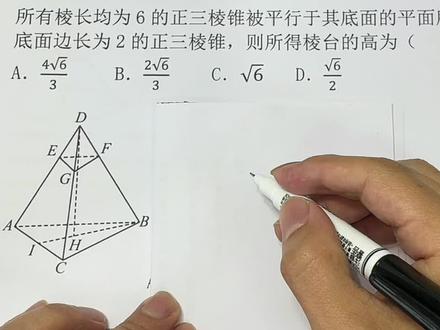 06:11查看AI文稿AI文稿
06:11查看AI文稿AI文稿这是一道立体几何里面关于三棱锥和三棱抬的一道题目,我们来看一下 棱长均为六的正三棱锥,棱长均为六的正三棱锥,那么他就意味着他其实是一个正四面体的吧, 每个边上都是六,然后他的每个侧面和他的底面,三个侧面和一个底面都是全等的正三角形啊,这样的话他才能叫做,呃,所有冷场均为六的正三棱锥 被平行于其底面的平面所截,截去一个底面边长为二的正三棱锥,画一个大的三棱锥啊,然后呢截去一个小的三棱锥,那这个因为这个大的三棱锥是个正四面体啊,是个正三棱锥,是个棱长均为六的正三棱锥,所以导致 这个上面的这个小的截去的底面边长为二的正三棱锥,其实也是一个每个棱长均为二的这么一个三棱锥,也就是一个正四面体 好则捷德所得到的这个棱台的高,那么这个棱台的高在哪呢?首先这个棱台呢,是不包括上面这个小 圆啊,小棱锥的啊,小三棱锥的,不包括的那只有个棱台的吧,那棱台的高呢?他应该也是过舵点,过顶上面的这个舵点,往下面这个投影点 h 点,这个舵 h 呢,其实是我们三棱锥的高, 可是我们轮胎的高在哪呢?所以我们把这个 doh 这条投影的这条垂直的线啊,与这个上底面 e、 g、 f 这 上底面他们相交的一个点,相交的一个点,把它叫做 p 点吧, p 点, 那么这个 p h 自然就是我们轮台的高了,所以我们要求的其实就是 p h 的 大小,那我要想求这个 p h 的话,我要把这个 p h 还是要放在这个 do h 里面去观察的,因为这个 p h 嘛,它本身并没有一个三角形存在啊,而 do h 确实有三角形的,因为有个 do h b, 而且这个三角形也是我们一个非常非常常用的 一个三角形,就是顶顶点的这个在底面的投影点,还有一个棱 啊,还有一个底面的这么一条线,他们三个组成的这个三角形啊,当我们这里是一个正是个直角三角形, 那么这个直角三角形其实是我们做类似的三棱锥的题目的时候啊,我们基本上都会去研究的一个图形,那么现在呢,我们要研究的是 p h 呀,所以我要知道这个 p h 与舵 h 的关系,所以我要模仿的 b h 啊,我在上面还要再做一个 p f, 把这个 p f 也给它连个线,那这样的话就有一个 door h b, 一个三角形,还有一个 door p f, 一个三角形,那么这两个三角形应该是相似的关系, ph 在这啊,但是呢,相似相似比是多少呢? 我们这个只是说了这个棱长一个是二,上面的小的棱长是二,对吧?下面这个是六,但是呢,因为他是一个所有棱长都相等的啊,所以这个斜边的这个 冷场,这个是二啊,这个舵 b 呢,也是六,那在我们这里呢,画一个平面图啊,一个二,对吧?还有一个舵 b 是六,那这样的话, do f 比舵 b 呢,就自然是一比三,然后呢,这边的舵 p 比 do h 也是一比三, 从而我们就知道这个 ph 啊,其实就是三分之二倍的 doh。 好,那 我要想求 p h, 那我就得先求多 h 了,而多 h 在哪里呢?多 h 在一个直角三角形啊,上面也是直角啊,多 h 呢,在这个直角三角形多 h b 这个里面啊,所以我要想求多 h 的话,我得求多 b 啊,多 b 我知道是等于六,那我还有一个 b h 不知道啊, d h 等于根号下舵 b 的平方减去 b h 的平方,舵 b 的平方我是得知道的啊,还有个 b h 我不知道,那 b h 在哪里呢?又在底面的一个三角形里面,所以我还得画一个底面的一个平面图,那在底面的平面图里面,因为他每个边长都是六 啊,然后呢, h 点其实是我们的一个重心啊,所以呢,我们就可以根据重心的性质啊,我们知道这个 bh 呢,他应该是三分之二倍的 bi 的, 而我们的 b i 呢,因为这里是三啊,这里是三十度,所以 b i 呢,一二杠杠三, b i 是三倍杠杠三, 那就三分之二乘以三倍根号三啊,也就是二倍根号三,二倍根号三呢,就是我们的 bh 的大小啊, bh 呢,往这里放的话,他变成根号下六的平方六六三十六,减去 bh 的平方四一十二啊,也就是根号二十四,根号二十四, 就是二倍根号六,所以多 h 是二倍根号六啊,多 h 呢,往这里填,那就是三分之二,再乘以二倍根号六,于是变成三分之四倍根号六,那么答案就选 a。 这个题在做的过程当中呢,大家要培养一个好的做题习惯呢, 就是画平面图这么一个立体几何的一个基本的习惯呢,希望大家从一开始接触立体几何就把它培养起来啊。 多画平面图,在平面图当中去讨论它的相似关系,讨论它的垂直关系等等。
 10:17查看AI文稿AI文稿
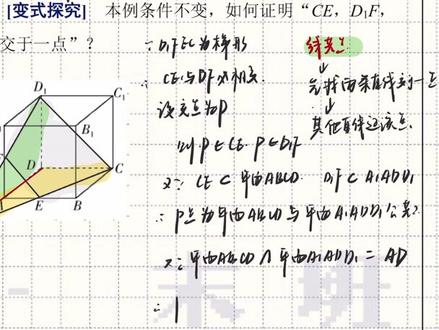
10:17查看AI文稿AI文稿大家好,我是末班班长,那我们一起来看一下空间点直线平面之间的位置关系,这一方面有什么样的类型题。首先考点一平面基本性质的应用, 那这一块呢,我们是要用一些基本事实来证明一些结论,包括这个点供面,以及我们线供点,还有点供线,这是三个不同方向的证明。那首先我们来看一下例一, ef 分别是 ab 和 aae 的终点, 求证 ecdf 这四点供面,那我们把这个平面给大家框出来。好,那就是这个灰色的平面,我们要证明这四个点都在这个平面之上,当我们遇到这样的点供面的问题的时候,点 共面我们会去怎么证明呢?既然有这么多点的话,我们可以先确定个平面用锁给的部分点, 当然这里也包括线点或者线供面,都是一样的思路,我们用所给的点或者线来确定一个平面,确定平面之后呢,我们只要再让 其他的点或者线在这个平面之上就好了,在平面内吧,用内这个词来更准确一点。那我们一起来看一下,这里面我们可以怎么去确定一个平面呢?那我们不难发现,这里有一组平行的直线,它叫做 ef 和我们的 cd 一平行直线,哎,就会有一个推论,叫做两条平行的直线能够确定一个平面,哎,那其实我们就已经完成了。第一步,我们用所 我给的线去定个平面,然后再去说明这些点在平面之上,这个证明题就搞定,那只要说明平行就好了,那怎么去说明平行呢?我们可以找一个中间量,因为 ef 是中位线的话,我们就会有 ef, 它是平行于 aeb 的。那我们怎么去证明 aeb 与 dec 平行呢? 我们可以去通过正方体这个条件,既然是正方体的话,我们就会有 abc, 不但平行而且相等,那这样的话,这个四边形他就是一个平行四边形,平行四边形我们就会有 ab, 他自然是平行于 dc 的。那我们用数学语言来好好整理一下证明。 首先我们可以第一阶段证明 ef 平行 aeb, 我们先连接 aeb, ef 和我们的 dec。 好, 因为 e, f 为 ab, a, a 一的终点,所以我们会有 ef, 他会平行于我们的 a, e, b, 那这是第一阶段。然后我们只要再说明,又因为 a, e, d, e, 他是平行于我们的 bc 的,并且由于正方形我们还有 aed 一,他是等于 bc 的,所以四边形 a, e, d, e, c, b 为平行四边形。 平行四边形我们就会有 aeb 是平行于 cd 一的,那我们就得到了 ef, 他是平行于 cd 一的,所以我们就能得到 ef 与 cd 一。可以确定一个平面,确定一个平面,我们给他整个名字,阿尔法。 哎,那四点供面,我们只要在说明一下,这些点都在这个平面之内,那因为 e, c, d, e, f 都是属于平面阿尔法的,所以 e, c, d, d, e, f 四点供面。 好,这道证明题就结束了,那这就是我们来证明点或者线供面的方法。首先呢,我们确定一个平面,然后只要证明这些点在这个平面之上就好了。或者有的题,同学们,你也可以把这些条件分成两部分,分成两部分, 你可以用这些条件确定出两个平面,分别确定平面阿尔法与贝塔,然后只要证明阿尔法是等于贝塔的,这两个平面相重合的,那我们也可以 证明这些点是供面的。那遇到这类题的时候,我们还会接着说明,那我们再看这个辨识,如果本地的条件不变,现在证明 c、 e、 d、 e、 f 和 d a, 我们要证明这三个点交易一点,那现在我们要证明的是限供点的问题。限供 点我们看这里一共有三条线,我们先找出两条直线交易点, 两条直线交于一点,然后再去证明其他直线过这个点就好了。 直线过该点。好,我们看一下这道题,那哪两条直线它是必然会相交的呢?我们可以不用太说明的呢?当然是 df 后面的 ce, 因为 同学们这个图形他必然是一个 t 型,这个四边形他是 t 型的话,那么这两个侧边他一定是相交的啊。因为 d、 e、 f、 e、 c 为 t 型, 所以 ce 与 df 必然会相交, 那我们就可以去设这个焦点,我们设这个焦点为 p 点的话,那接下来我们只要说 ad 这条直线他必然是过 p 点的就好了。那同学们到我们延长之后,这里出现了两个平面,一个是这个平面,另外一个是这个平面, 那 a、 d 充当什么角色呢?也充当这两个平面交线的角色,那 p 点又是这两个平面的 公共点的话,根据我们的基本定理,我们知道如果两个平面之内有一个公共点的话,就是这个批点,现在有一个了,必然会有过该点的公共直线,也就是我们的 ab 这条直线。好,那我们说明一下,则我们首先得说明他是公共点, 则 p 它既属于我们 c、 e 这条直线, p 又属于我们 d、 e、 f 这条直线,那又因为 c、 e 它是在我们的平面 a、 b、 c、 d 之内的,而 d、 e、 f 是在我们平面 a 一 a, d, d、 e 之内的,所以 p 点为平面 a、 b、 c、 d 与平面 a 一 a、 d 第一的公共点。然后呢,我们只要说明 a 是胶线就好了,那又一位平面 abcd 胶平面 a 一 a、 d 第一,他会交在 a、 d 这个公共直线上,这是正房体已知的条件了,所以我们就能得到,所以批点他一定是在 a、 d 之上的。那我们就已经说明了,两条直线交于批点,而 a、 d 这条直线也会经过批点,所以 c、 e、 d、 e、 f 与 d、 a 是教育一点的, 就交于这个批点。好的,这是我们关于限供点的问题,怎么去处理?先找两条直线交于一点,再证明其他的直线经过这一点,我们把它标一下。哎,这是方法啊,上面这里点供面也是一样的。 好,那我们接着看练习里面给大家放了一个点贡献的问题,其实点贡献的话也是同样的思路,我们看四个点嘛,我们先是证明两条直线过一点,所以点来说,我们只要证明两个点,先定一条直线,再去证明其他的点在这个直线上就好了,这是通常的思路啊。 点贡献的话,一,我们可以先找两点,找两点定直线,再去证明其他的点在直线上,其他点直线上,我就简介了啊, 哎,这是第一种情况,那第二种情况,我们看这道题里面这四个点他是比较特殊的,为什么呢? ab 是平行于 cd 的, ab 平行于 cd, 说明这两个直线他是能够确定一个平面的,那么 efgh 你发现他都是这两个平面的公共点,所以这 公共点必然是贡献的,你只要把这个事情陈述起来就好了,哎,所以第二种情况就是这种特殊的情况,所有的点在一个特定的直线上, 这里我们指的就是交线了。那我们把这道题好好陈述一遍证明,因为我们 ab 是平行于 cd 的,所以 ab 与 cd 可以确定一个平面, 一个平面,哎,阿尔法已经有了,那就设这个平面为贝塔。然后我们需要说明的是这四个点分别是这两个平面的公共点,那我们可以说一个,哎,其他的同理就行, 那因为 e 是属于平面阿尔法的,且 e 是属于平面背他的,也就是说明 e 为平面阿尔法与平面贝塔的公共点。 同学们写证明的时候一定不要跳步啊,这个很有利于你自己对思路的整理,也有利于判决。老师看清楚你的逻辑。好,公共点之后,我们同理 f、 g、 h, 他均为平面阿尔法与平面贝塔的公共点。 那又因为我们知道两个平面如果有公公点的话,则他们有且只有一条直线,一条过该点的 公共直线,所以就说明了 e f、 g、 h 四点 b 定 贡献。好,那这样子这道题我们就证明完了。我们看一下这是考点一,我们分别整理了一下怎么去证明点供面,怎么去证明线供点和点供线,那我们接着来看考点二,空间两条直线的位置关系。
274数学末班班长












