拉普拉斯变换如何转化为频域
拉普拉斯变换是副理业变换的升级版,是的,你没有听错,就像功能手机升级到智能手机一样,非常厉害的。那么为什么要升级副理业变换?又有哪些问题呢? 你可能觉得复理业变幻已经很强大了,既然这么强大,那除了处理信号之外,能不能用它来干点别的? 比如解危分方程?还真有这个可能,因为复理业变换有一个重要的性质,那就是函数 n 解导数的复理业变换等于其复理业变换乘以 i o m a, g r 的 n 次方。 现在有一个微分方程, y 的二节导数加 y 等于负的 f。 解微分方程就是要把 yt 的函数解析式求出来。我们将微分方程的等式两边同时进行 行复理页变换,再利用函数倒数复理页变换的性质,就能把微分方程变成简单的代数方程了。这里的大 f omega、 大 y、 omega 分别是小 ft 与小 yt 的复理页变换, 这样就很容易求出大 y omega, 然后再通过复理页逆变换就可以得到 yt, 很完美,像变魔术一样就把微分方程解出来了。 这就是传说中的解危分方程的神器吗?还不能高兴的太早,马上就要面临问题了,因为富力爷变幻存在着比较严苛的限制条件,他要求函数必须是有限个断点,有限个集值, 最重要的是他要求函数绝对可击,意思就是信号函数在富无穷到正无穷上必须是有限的,因此无数的常用函数,诸如指数函数、 二次函数,甚至连常数函数都不能进行复理页变换。与此同时,复理页变换在处理信号衰险的时候也面临困难。比如在物理学中,单摆的运动会被看作是一种简协运动, 用一个关于时间的函数来表示他近似于一个正弦曲线。用复理页变换就能得到更简单的疲欲表达,看起来很完美,但是在自然界中却无法真正找到这样的间隙运动,因为真实世界总会受到阻尼的影响,所以实际的运动函数可能是这样的。 事实上,单百会按照一种指数衰减的模型逐渐变小。自然界中有许许多多现象符合指数衰减的规律,比如地震波的传递,放射性物质的衰变。再比如人们记忆的遗忘曲线护理液变 换能告诉我们函数中存在哪些正弦曲线,却不能很好的处理衰减因素。如此一来,拉普拉斯变幻便应运而生。拉普拉斯变幻本质上是复利业变幻,更一般的泛化形式。为了说明什么是拉普拉斯变幻,我们通过一个例子来展开接下来的讲解。 对于不满足复理页变换要求的二次函数 f t 等于 t 的平方,把这个函数乘以一个衰减系数 e 的富伽马 t 次方。这样一来,当 t 趋于无穷大的时候, t 的平方乘以 e 的富伽马 t 次方,在无穷大处的极限是零。 为了把小于零的部分过滤掉,我们再乘以一个单位积月函数,这样就可以得到一个可以进行复理页变换的新函数 g t 了。把 g t 的复理页变换展开,在 把指数部分合并到一起是这样的。然后把伽马加 iomega, 用一个复数 s 代替,这就是拉普拉斯变换,它是一个从食欲到复数欲上的积分变换,其中复数的虚部代表频率,食部代表着衰减因子。 这个函数的输入输出都是负数,所以涉及到四个变量,它的图像可以用一个立体图形来表示。 输入 s 用负平面上任意一点表示。输出 fs 的模长用 s 到曲面的垂直距离来表示,而 fs 的香味就用颜色来表示。 当你把图像画出来,就会知道,复里叶变换其实是三维图像中伽玛等于零时的切面,也就是过须轴的那个切面。这就是为什么拉普拉斯变换使复里叶变换更一般的泛化形式。 现在我们可以结合衰减系数,把任意的函数分解成若干代指数衰减因子的正弦函数的线性组合。这样一来,我们就可以按照真正的衰减规律分解信号了。 更重要的是,拉普拉斯变换没有复利业变换那么多的限制条件,他可以轻松地用于求解微分方程。 现在我们去试一下函数一阶倒数的拉普拉斯变换是这样的,二阶倒数的变换是这样的。再回到刚才的微分方程, y 的二阶倒数加 y 等于负 f, 对方程两边同时进行拉普拉斯变换就是这样的。同样的道理,我们可以得到关于大 ys 的代数方程。求出 ys 之后,再进行拉普拉斯逆变换,就可以求出函数 yt 了。因为不存在复利 变换那样的限制,他对于大多数函数都适用,所以他被广泛用于求解线性常微分方程、偏微分方程和积分方程等问题。怎么样?关于拉普拉斯变换你了解了吗?今天的讲解就到这里,您可以关注梯度世界,了解更多精彩内容。
粉丝2.7万获赞7.6万
相关视频
 14:23查看AI文稿AI文稿
14:23查看AI文稿AI文稿这是接月函数 ft 等于一 t 大于等于零的拉普拉斯变换。小窗介绍的是他在描述简邪运动中作为外部激励函数展示的二维图像 对应视频。在本号的微分方程专栏和复利业变换专栏掌握本篇各个小窗里的内容,对理解本视频的三弟直观解释至关重要。 拉普拉斯变换在工程学、物理学和数学上扮演着非常重要的角色。拉普拉斯变换让我们能够评估一个系统的稳定性和频率响应。 拉普拉斯变幻还为我们提供了一种轻松求解微分方程的方法,把微积分变成了袋数。请大家注意,在本视频中有时间轴拖动的动画,时间轴代表函数输入,自变量替负平面代表两维的 ft 输出。如果再输入 s, 则还需要额外的两维,五维无法展示,所以 s 被设为无数负值中的一个定值,即当成常量。大家看到的螺旋线只是无数条线中的 s 等于此值的一条。 在本视频中,颜色表示一个函数的向位信息, 虚竖的向位,用旋转的白色线与正时轴之间的夹角来表示。 虚数的扶直,用旋转的白色线的长度来表示。这条线是 s 等于零点一加 i 时,函数 e 的 st 四方的图像。当 s 在负平面上任意取值时,对应无数条这样的螺旋线。 在 f, s 等于 s 分之一。这个频域函数中有时也叫 f 域,不存在时间信息,没有时间这个字变量。此函数的输入是一个虚数。虚数的十步和虚不值可以从两个坐标轴上读出, 落下的每颗珍珠代表一个负数。输入击中的点有两个含义,一是代表圆函数与饥函数乘积的积分函数, 二是代表元函数在拉普拉斯变换后输出的 s 与函数的值。此函数的输出也是一个虚数,他由图形的高度和颜色表示,高度由垂直于 于实轴和虚轴的一维轴给出,颜色则代表了第四维。图中每个点的高度代表输出的符值,颜色代表输出的向位。 图中现在看到这个拉普拉斯变换后的函数中,输出和输入完全相等,都为 s。 他的原函数是迪拉克 dlat 函数的一阶导函数,而这个拉普拉斯变换后的函数,他的输出等于输入的导数。前面说了,他的原函数是接月函数。 当 s 为何值时,这个频域函数存在,或者说圆函数的那个积分函数收敛在这里,当 s 的时步大于零时,函数存在。 这个例子中的函数,我们称之为频喻函数。与夏文中的 直遇函数对应, 十月函数就是时间的函数,此时大家看到的是接月函数 ft 等于一。 每个十余函数都有一个相关联的频域函数,他们之间的转换我们称之为拉普拉斯变换。 这种变幻很有美感,但是为了理解他,我们需要先谈谈指数函数的相加。 对于时间的函数来说,变量 s 永远相当于一个长数, ft 等于扶直乘以向位。 如果我们使 s 的虚步变大,白线的旋转会加快,频度会升高,而且幅值也会增大。 如果我们使 s 的时部变大,扶直会升高的比之改变虚步更快。 如果 s 的时部为零,这时是复立业变换,扶直会维持在虚步确定的直上,如果虚步不变,则扶直也不会改变。 我们把我们的函数乘上一个长数, 在这个例子里,不妨设这个长数为十数三, 不过这个长数也可以是一个虚数。 现在来看看,当我们像这样让指数函数相加会发生什么。 所有的波形都可以通过这种指数函数叠加的方式制造出来。 波形的拉普拉斯变换告诉我们每个指数函数要添加多 多少。 如图,我们画一条无限长的直线, 这条线可以在任何位置上。 当这条线固定在一个位置上,每一个这样的点就代表一个指数函数,而这些指数函数就是我们用来叠加生成波形的 复数。 s 就是每个点在实轴和虚轴上的位置。 对于这些点中的每一个,我们加上这个关于时间的指数函数。这里的 s 可以被视为一个长数,用前面大家看到的天上撒下来的珍珠来表示,这是 s。 取一个定值时 e 的 st, 四方的三为图像,一为输入,二为输出。 每颗珍珠放到指数函数异的 st 次方里,再都与一个虚数相乘,这个虚数便是拉普拉斯变换的频域函数的值。用这条珠链上的红珠子表示,红珠子对应图中在这个位置的高度和颜色,代表虚数的浮直和浮角。由于我们有 无穷多个点,每个点代表的是函数,这样的函数相加很容易变成无穷大,除非我们也乘上一个无穷小的数,也就是这些点的间距。 由于这些点的间距接近于零,所有这些指数函数的加和可以表示成这样, 我们将结果乘上图中的这个长数, 就得到了我们关于时间的元函数。这是拉普拉斯逆变换对应的积分,也叫布罗姆维奇积分或富丽叶梅林积分。梅林逆宫式是用线积分得到的实数 c 表示直线的未 位置是 s 的十步,十步不变,在虚步上积分。 由于 c 可以取无穷个值,这条线可以在无穷多个位置,所以有无穷多种方法来创造我们原来的波形,即得到无穷多个元函数。 如果我们把线移动到 s 的时部为零的位置,那这就是一个特殊情况。我们要只用正弦曲线来生成波形,就像复立液变换一样。小窗展示复立液变换的二维图像,与本三维图像描述的是 同一个数学场景,但小窗因为缺少时间轴而借用了副虚轴。动画表现的是一对角速度相反的信号相加,他的虚步互相抵消,只剩下十步叠加后的函数在十轴上震荡。 现在是两对角速度相反的信号相加的动画,小窗也是,但此时主画面的情况跟刚才不同,因为拉普拉斯变换的 s 十步步为零,虽然信号相加时把他的虚布抵消了, 叠加后的函数还是在实轴上震荡,但震荡幅度在发散,这时已经是拉普拉斯变换。小窗的情况则跟前面类似,还是复利液变换 s 时不为零,震荡幅度不会发散。 拉普拉斯变换比复理液变换更具有普遍性,因为用拉普拉斯变换,我们也可以将 垂直随时间变化的丧影曲线叠加。那如果反过来,我们已经知道了我们的波形是什么样的,怎样得到他的拉普拉斯变换呢? 看如下的表达是,我们在长数 s 前面有一个符号, 将这个表达是乘以我们想要找到其拉普拉斯变幻的函数的波形, 在这里是接月函数。 ft 等于一 t 大于等于零,他的定义率在大于等于零,所以为负的情况可以引去。 在这个乘法运算的结果里,每一个时刻是一个用箭头表示的负数, 通过如下方程把所有的箭头加起来就是积分。 结果是一个用白色箭头表示的负数,而这个用白色箭头表示的负数就是我们的波形。再取值为 s 十的拉普拉斯变换。 如果积分的结果为无穷,我们就说在取值为 s 时,波形的拉普拉斯变换不存在。 这种情况是存在的。例如,当这个 s 的实布是一个很大的负数时, 这就是为什么在我们的例子里,当 s 的实布为负数时,拉普拉斯变换不存在。 当决定在哪里划线来恢复我们的原始波形时, 我们需要把它画在对于当前波形拉普拉斯变换存在的地方。
457锦南高研院 05:27查看AI文稿AI文稿
05:27查看AI文稿AI文稿拉普拉斯变幻是护理液变换的升级版?是的,你没有听错,就像功能手机升级到智能手机一样,非常厉害的。那么为什么要升级护理液变换?又有哪些问题呢? 你可能觉得复理业变幻已经很强大了,既然这么强大,那除了处理信号之外,能不能用它来干点别的? 比如解危分方程?还真有这个可能,因为复理业变换有一个重要的性质,那就是函数 n 解导数的复理业变换等于其复理业变换乘以 i omega 的 n 次方。 现在有一个微分方程, y 的二节导数加 y 等于负的 f。 解微分方程就是要把 yt 的函数解析式求出来。我们将微分方程的等式两边同时进行 行复理页变换,再利用函数导数复理页变换的性质,就能把微分方程变成简单的代数方程了。这里的大 f omega、 大 y、 omega 分别是小 ft 与小 yt 的复理页变换, 这样就很容易求出大 y omega, 然后再通过复利业逆变换就可以得到 yt, 很完美,像变魔术一样就把归分方程解出来了。 这就是传说中的解危分方程的神器吗?还不能高兴的太早,马上就要面临问题了。因为富力爷变幻存在着比较严苛的限制条件,他要求函数必须是有限个断点,有限个级值, 最重要的是他要求函数绝对可击。意思就是信号函数在富无穷到正无穷上必须是有限的,因此无数的常用函数,诸如指数函数、 二次函数,甚至连常数函数都不能进行复理页变换。与此同时,复理页变换在处理信号衰险的时候也面临困难。比如,在物理学中,单摆的运动会被看作是一种简协运动, 用一个关于时间的函数来表示,它近似于一个正弦曲线。用复利页变换就能得到更简单的疲欲表达。看起来很完美,但是在自然界中却无法真正找到这样的间隙运动,因为真实世界总会受到阻尼的影响,所以实际的运动函数可能是这样的。 事实上,单百会按照一种指数衰减的模型逐渐变小。自然界中有许许多多现象符合指数衰减的规律,比如地震波的传递、放射性物质的衰变。再比如人们记忆的遗忘曲线,复理液变 患能告诉我们函数中存在哪些正弦曲线,却不能很好地处理衰减因素。如此一来,拉普拉斯变幻便应运而生。拉普拉斯变幻本质上是复利业变幻,更一般的泛化形式。为了说明什么是拉普拉斯变幻,我们通过一个例子来展开接下来的讲解。 对于不满足复理页变换要求的二次函数 f t 等于 t 的平方,把这个函数乘以一个衰减系数 e 的富伽马 t 次方。这样一来,当 t 趋于无穷大的时候, t 的平方乘以 e 的富伽马 t 次方,在无穷大处的极限是零。 为了把小于零的部分过滤掉,我们再乘以一个单位积月函数,这样就可以得到一个可以进行复理页变换的新函数 g t 了。把 g t 的复理页变换展开,再 把指数部分合并到一起,是这样的,然后把伽马加 iomega, 用一个复数 s 代替,这就是拉普拉斯变换,他是一个从食欲到复数欲上的积分变换,其中复数的虚部代表频率,食部代表着衰减因子。 这个函数的输入输出都是负数,所以涉及到四个变量,它的图像可以用一个立体图形来表示。 输入 s 用负平面上任意一点表示。输出 fs 的膜长用 s 到曲面的垂直距离来表示,而 fs 的香味就用颜色来表示。 当你把图像画出来,就会知道,富里耶变换其实是三维图像中伽玛等于零时的切面,也就是过虚轴的那个切面。这就是为什么拉普拉斯变换使富里耶变换更一般的泛化形式。 现在我们可以结合衰减系数,把任意的函数分解成若干带指数衰减因子的政协函数的线性组合。这样一来,我们就可以按照真正的衰减规律分解信号了。 更重要的是,拉普拉斯变幻没有复利业变幻那么多的限制条件,他可以轻松地用于求解微分方程。 现在我们去试一下函数一阶导数的拉普拉斯变换是这样的,二阶导数的变换是这样的。再回到刚才的微分方程, y 的二阶导数加 y 等于负 f, 对方程两边同时进行拉普拉斯变换就是这样的。同样的道理,我们可以得到关于大 ys 的代数方程,求出 ys 之后,再进行拉普拉斯逆变换,就可以求出函数 yt 了。因为不存在复利 变换那样的限制,他对于大多数函数都适用,所以他被广泛用于求解线性常微分方程、偏微分方程和积分方程等问题。怎么样,关于拉普拉斯变换你了解了吗?今天的讲解就到这里,您可以关注梯度世界,了解更多精彩内容。
435返朴 16:35
16:35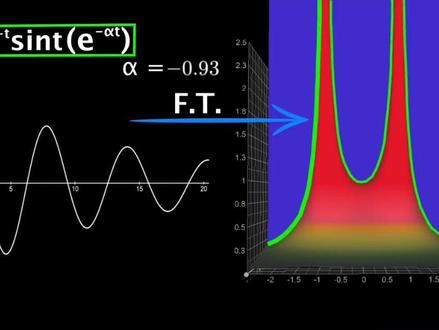 01:04
01:04 00:056658九章数学社
00:056658九章数学社 03:29查看AI文稿AI文稿
03:29查看AI文稿AI文稿这个 s 是什么? s 等于 l f 加 l mag, 我们将其带入方程式中,再拆分指数项。 如图所示。当 l 发等于零时,本是与复利液变换完全一样。当 l 发不等于零时,本是就像是一个带有额外像的复利液变换。本质上,复利液变换是一个正弦波的扫描器, 拉普拉斯变换则不但扫描正弦波,还扫描指数项。扫描方法也是通过前面讲的面积, 设有函数 f t t 从零开始取值。拉普拉斯变换是这样,先像以前一样乘以 cosen, olagt 和 saomagt, 然后多乘一个指数相应的负 flt 次方。 两个柿子对应的面积的直就是前面讲的直角边的长度。举一个具体的例子,先绘制一个衰减的 cos omax t。 我们需要两条轴来作为拉普拉斯变换的输入,一个用于 omaga, 又名正弦曲线,另一个用于 l fr 叫指数曲线。 f 等于零和 omax 等于零时,则指数项为一,撒印部分为零, cocon 部分的积分为零点零五及福值。我们现在不画输出图,所以把零点零五先系到输入轴边上,方便理解。我们保持 l f 不动,改变一下 omag, 这会将输入点沿虚轴向上移动。我们观察面积如何变化。 当 omex 等于三时,再次捕捉到左上图像,所有面积都升到 x 轴上方,没有负面积的抵消。因此扫描仪在原始函数中找到了 coson 三 t 的成分,但是 他的积分是一点零一,一个有限的值。我们其实期待在这里得到一个无限大的面积。一点零一的值跟前面的那些值的输出没有什么特别之处,于是我们现在开始改变 f 的输入值,先把正弦方程删除掉, 因为三 a 三 t 乘以 cos 三 t 的积分在零处震荡,相对来说可以忽略不计。一旦我们达到 f 等于负零点五,指数衰减就消失了,因为两个指数相约掉了。我们终于得到了期待中的无限大的面积。 无限大的面积意味着我们的扫描仪不仅发现了正线曲线,而且还发现了 ft 的原始函数中的指数项及他的系数。 只是别忘了,指数项还有个符号。强调一下,在图上画出这些无限大的面积的点是我们最关注的事情之一。 我们把他们用 x 标示出来。对于那些需要了解零点图和几点图的同学来说,实际上只需找到几点,并查看相关的 y 坐标和 x 坐标,因为那些坐标会告诉我们方程中的正弦曲线和指数,几乎所有想知道的信息都在里面。 相对几点来说,图上的大部分区域的值是有限值或接近于零,这些值对我们的目的来说并不重要。该图如此有用的原因是因为许多系统,如 rlc 震荡电路,弹簧震子的简邪运动, 还有通用控制系统等都会产生正弦和指数输出。所以我们需要一个比富丽叶变换更强大的拉普拉斯变换来再次分析这些。有一个关于拉普拉斯变换的完整视频,包括可视化的三 d 动画, 大家可以参照观看。在本专栏里,拉普拉斯变幻与富丽叶变幻的扶植图和几点零点的意义,我们下期视频再见。
190锦南高研院 14:52查看AI文稿AI文稿
14:52查看AI文稿AI文稿同学们好,我们今天讲拉布拉斯变换与反变换, 第一节呢是拉布拉斯变换的定义,那这个呢是一个数学的一个课程,属于积分变换的里面的一个内容,那么拉布拉斯变换法呢, 他的核心呢是把时间的函数跟复变函数来进行联系起来,大家注意看到这个符号时间函数呢是 ft 关于时间的一个关系,而他呢跟这个复变函数,复变函数呢,他是 f s 大写的 fs 这样连起来,那他是把食欲的问题呢,通过数学变换来变换成个富平域的问题。 那我们前面呢,动态电路的十一分析里面呢,有一些呃高阶的不用方程,比如说二阶不用方程,三阶不用方程等等的,那么他就可以变成关于平域上面的一个代数方程来进行求解, 也就是说呢,通过这个拉布拉丝变换,我们实际上呢是可以把高阶的微风翻整的,那么给他进行简化,简化成带出方程,这样子的来求解的时候呢,就比较容易一些啊。因此呢,我们利用拉丝变换法进行电路 分析,他就成为了电路的富平与分析法,又称为运算法,大家注意看到这个名词叫运算法,那我们后面呢就会介绍这个运算法在动态电路当中的一个分析。 那首先呢,我们先介绍一下拉普拉斯变换,我们常见的一些变换,比如说像对数变换,那么可以把乘法的运算变成简单的加法运算,这个是对数运算, 也有呢我们电路当中所学到的项链法,那么他可以把食欲下面的政权运算呢,变换为 不速应算,那这个经过一定的变换,那么对我们分析问题来说呢,有一定的简化,所以我们拉布拉斯变换法呢,那么是把十亿下面的原函数 跟平域下面的下函数做一个对应, 那么具有多个动态原件的这种普杂普杂电路呢?它的电路方程肯定将会超过二阶,那么我们前面已经分析过二阶电路了,它的 解呢是比较复杂的一个解,所以利用拉布拉斯变化法, 它可以通过积分变换,可以把已知的十余函数变换为富平余函数, 那么就得到一个代数方程,关于富平域的一个代数方程,代数方程求出来他的一个富平域下面一个解以后呢,再进行反变换 啊,这面有拉拉普拉斯反变幻,可以回到原来的食欲下面,那这时候呢,就可以得到满足我们电路初始条件的原来的威风方程的解啊,整个过程呢就是这样子的, 首先我们列写一个食欲威风方程,然后呢对这个方程呢进行拉普拉斯变换,得到一个 平域下面的带出方程,那这个带出方程呢?求解出来以后,他的解呢?来进行拉式反变换,然后得到最终食欲下面的解啊,这个就是一个呃 运算法,它的一个分析的过程,它的优点呢,就不需要去确定积分的长数,也不需要 建立啊,或者是求解这个无人方程,这个使用于高阶复杂的动态电路。 好,我们看一下具体的拉斯拉普拉斯变换和反变换的定义,我们定义呢,在零到正无穷期间,这个时间函数 ft 呢?他的拉布拉拉布拉斯变换式是这样一个关系式,一个是他的正变换,上面这个是他正变换的红色 fs 呢,等于 ft 呈上 e 的副 st 之咪,然后对整项呢,从零负到正无穷进行积分啊,对 t 进行积分,这个是大巴士正变换, 反变化呢,也有相应的四指,那这个反变化呢,不是我们重点掌握内容,我们重点掌握内容呢,是正变化, 那这边的话呢,是对一个十一的函数呈上一个指数函数,然后呢一个积分的关系式减写呢,我们可以写成 fs 等于 lft, 那如果是反变化的话呢,就是 l 上面呢,上标写一个负一 f s 啊,大 s, 大写的 f s, 注意看这个大写和小写的关系, 那这里面呢,所对应的 s, 我们把它定义成叫做复频率,复频率呢,具体是等于可 c 加上 jome 感这样一个复频率的, 那需要注意他的积分域,我们积分域呢,有从零负开始,那这个是叫做零负的拉屎变化,那我们基本上我们讨论的都是从零负开始,那这样零负开始呢,有个什么好处呢?他就可以涵盖了零负 复到林正以及林正到正无穷之间的一个关系。这个主要是涉及到什么东西呢?涉及到函数呢?如果是冲击函数的时候,那这时候呢?林副到林正,那么他去解的话呢,是可以解出来这样有关系的 啊,这个是第一个注意事项,第二个注意事项呢,就是这个下函数它存在的条件, 那么这里面呢,我们定义的对 ft 乘三亿的副 st 之谜,它的绝对值,从零负到正位重新积分,它是原小小于这个胸大的, 那这时候呢,就存在了一个有限的长数 m 和 c, 使得函数呢 满足这种关系, ft 的绝对值小于等于 m 乘在 e 的 ct 次咪啊, t 是在零到重从期间的大一点零的, 那因此呢,我们把这个积分一下, 最终得到一个积分的式子,就等于 m 除以 s 减 c, 那么这时候呢,就表示说 ft 的拉丝变换式 fs 呢,总是存在的,因为呢,总是可以找到合适的一个 s 的值,使得上面这个式值呢,积分是有限值, 比如说不会去无穷大。 第三个是我们非常注意的一个内容,就是下函数,他都是用大写字母来表示的啊,上面也不带点, 比如说电流 i, 那么就是大写的 i, 大写的优 原函数 ft 呢,用小写字母来进行表示啊,用小写的 iu 来进行表示。好,大家注意看以后呢,我们这里面的这个下函数括号里面呢是 s, 括号里面是 s, 表示呢,它是一个富平域上面的一个函数关系啊,那接下来我们来看一下典型函 数的拉丝变换,那主要呢,就是通过这个拉丝这边换,这边换的一个关系式来进行分析,比如说第一个单位的接函数的下函数, 那这时候呢, ft 呢,等于一不小心,我们对这个一不小心呢成善意的副 s t 之咪,然后进行从零负到正不从进行积分,那这时候积分的关键是呢,就等于 啊,因为 t 大于零,以后呢,这个一不小 t 呢就等于一,所以就是一乘三一的负 s t 之命。 那么把这个进行积分的话,就等于负的 s 分之一,乘上 e 的负 s t c m 从零负到正无穷经得到了他的一个关系值,因此呢,最终的值就等于黑十分之一,那也就说单位级的函数,他的下函数呢,就 等于 s 分之一。那如果是单位冲击函数的话,一样的把这个单位冲击函数呢,给他带到这个正面换的第一次里面去,那我们 这个从今而数呢,只有在零负到零正之间有他的一个关系时啊,有他的就值,因为零正以后呢,他等于零了啊,所以就是等于零负到零正之间的这有一个关系值, 那么零分到零证之间的时候呢,他是等于一的啊,所以这个他的积分呢,就最终就等于一,因此呢,单位冲击函数,他的下函数呢,就等于一。这些这个结论呢,需要大家记住, 指数函数 e 的 at 痴迷, e 的 at 痴迷呢?因为在我们食欲下面,这个 是非常重要的一个函数关系啊,所以我们把这个他对应的象函数给他求解一下,一楼 atsp 带进去,那么这个时候呢,他的结果就变成了, e 的负, s 减 a 的差值呈上 t, 是咪?然后呢,前面呢一个系数就是负的 s 减 a 分之一,然后呢,令他从 正无穷到零负进行取值,最终的结果呢,等于 s 减 a 分之一 s 减 a 的导数,那也就说呢, e 的 比如说 e 的负二 t 之咪,它对应的下函数是什么呢?那这时候他对应的下函数, 那就是 s 加二还减二, s 加上二分之一,这个就是他的一个呃, 下函数啊,那下函数 e 的负二 t 次咪就是 s 加二分之一,反过来你要能够知道, s 加二分之一,他的这个原函数就是 e 的负二 t 次咪 啊,这个是相当于有一个拉丝正变换,跟拉丝反变换有关系。 第四个时长数的一个下函数,一个 k 值, k 值存进去,那么这时候呢,拉式变化呢,就等于 s 分之 k, s 分之 k, 那也就说呢,如果一个时数 他是等于二,那这时候呢,他对应的这个向上数就是 s 分之二啊,一对应的向上数就是 s 分之一啊,五对应的他的向上数就是 s 分之五 啊,这个用在什么地方呢?这个用在呃,电源,电压源,电流源上,直流的电源上啊,比如说这一个直流的电压源,他是十伏的一个电压源,那这个时候呢,要 用运算法来分析的话呢,那么他的一个什么呢?他的下函数就等于 s 分之十, s 分之十啊,就是需要注意,这是时长数啊,最后一个单位延迟接函数英雄替减大 t 的一个下函数,那这个延迟函数呢?我们把这个具体的一个关系呢列写出来,那么把它带入到这个拉丝正面换的四指名去,最终的值就等于 s 分之一,乘上 e 的负 s 大 t, 这个是延迟结函数,那这个呢,大家简单的看一下就可以了,这个用的倒是不多, 那么因此呢,这么有个推论,那么对任何一个函数进行延迟的话呢,那么对视就是对任何一个下函数呈上一个亿的负 s 大 tc 啊,这样一个关系, 像这个呢,呃,用的不多哈,大家简单看一下就可以了。最终我们小结一下,什么是拉丝变换, 什么是拉丝反变换,什么是原函数,什么是下函数,两者之间有什么关系?那么拉式变化呢?就是已知原函数求下函数的这个过程就叫拉式变换,而已知下函数求原函数的过程呢,那就变成拉式版变换。 那么我们所对的原函数指的就是这个食欲下面的函数用小写的字母来表示,而下函数呢,它是一个富平原函数,用大写字母来表示 原函数的拉丝变换就得到下函数,而对下函数的拉丝反应换最终得到的就是原函数,这个他是他们之间的关系。
50仇敌三千奈我何 04:46查看AI文稿AI文稿
04:46查看AI文稿AI文稿大家好,这次我们来看一下这个用拉丝变换法来分析一个具体的电路,这个电路嘛,一般他是包括电阻、 电杆和电炉,那我们看电主的福安关系就这样了,对吧? u 等于 r i, 这个 u 呢? i 呢?都都用那个拉丝变换来表示,这这个都简单,那电杆呢?就是 u 等于 二五 di 除 dt, 这个呢是用到用到这个这个拉丝变换的微分性质,这个推出来是这个样子啊,这个也可以变成变成这个悠悠,这里也可以变成这个,这个是等效电路,我们看到这这个是这个的等效电路,你看我们看到这两端是 us, us 等于这个电压减掉这个电压,这个电压就这个这个因为这个是敢敢抗嘛,敢抗 烫就相当于电阻,电阻成这个电流就相当于这个电压,就就就这个电,这个是一个,这个是一个电压元,电压元,我们把这个电压啊剪掉这个电压,那就是这个电压了,对吧? 这个电压的大小就是这个,他的方向是这跟这个反过来的,所以是这个电压减掉这个电压等于这个电压,这个就是把电流分成两部分,上面是一部分,下面是这这一部分,这个这是等效电路,这是电感的等效电,这个电容还等于 c d u 除以 d t, 这个这个 是用他的微分性质,这跟刚才的一样的一样。等一下,那么我们在这个电路里面要用到这个 k c l k v o 就是 k c 后铺电流定律和 k c 后后后后后伏了那个电压定律。我们来看一下这个电路,这个电路把他的那个方程列出 来就是这个样子,这里有一个电阻吗?对吧?这个这个电压就是 is 了这个电容,他的电压就是就是这个这个电杆电压就是这个,然后剩下的是这个这个这个电压,对吧?这个电 我们看这个电路就是把刚才的那个那个那个方程列出来,他他这这个这个方程就是这个样子, 这个样子,然后对方程左右两边分别进行拉普拉斯变换,就变成这个这个 u, 因为这个 u 是一个长数,长数的拉普拉斯变换,他是等于这个 s 分之一, s 分之一的这个自己看一下,求求一下就知道了。所以他他整个变换以后,拉普拉斯变换以后他是这个样子,然后再 再再对他进行那个求解,求解这个就就就这样解了,这样把那个几点求出来, 然后再啊再把它分开来,分开了,然后就得出了这个爱是这样的,这个就是就是这个这个这个求解的过程。然后我们再看第二个例子,这个就这样的一个例子,其实跟前面的那个差不多, 就是把他的那个电路方程列出来,然后求求出一个个这个把一个个起点求出来,然后再再把他的 ut 求出来,这个这个题目是求 ut, 这个题目呢是求电流,所以这个都是都是可以的, 这个电流是已知的,对吧?他要我们求的是这个 ut 哈,这个是已知的,所以求出来的结果是这个,那这一张还是相对简单的,他这个整个的那个拉 plus 变换呐,他其实就是为了解决富力液变换里面这个 ft 啊啊,不能, 不一定绝对可及的这样的矛盾,他就是在在这个基础上,在复利业变换的基础上啊,成了一个一个衰减因子, 成了一个这样的衰减因子之后,然后就强强制把这个 ft 变为那个绝对可及,这个就是拉克拉斯变换的根本意义所在。 同时呢,由于这个拉普拉斯变换的微分特性,微分特性和积积分特性和积分特性啊,这个微分,这个是积分特性,所以呢,这个拉普拉斯变换他又可以用于这个求解那个微分方程, 我们刚才分析的这个电路呢,这这样,这这这样的方程就是一个微分方程,我们就可以通过拉普拉斯变换的很方便的求解出来,利用他的那个微分特性和积分特性,这个就是 这些,这些这几点呢,就是那个拉普拉斯变混的主要特点和作用,就是跟那个富丽叶变混比较哈。 还有拉布拉斯变换分为双边拉布拉斯变换,好像是单边拉布拉斯变,那双边拉布拉斯变换他会出现这种情况,就是当那个向函数相同的时候啊,他收敛欲不一定相同, 所谓的双双边就是这个积分线负无从到正,无处,单边拉不拉丝,拉不拉丝边环,他就是从零到无处,所以一般呢,那个那个,因为这个时间总有一个起点,所以我们这个主要讨论的是这种单边拉不拉丝边。
 14:52查看AI文稿AI文稿
14:52查看AI文稿AI文稿通常大家都会困惑,拉普拉斯变换是从哪里来的?一种理解拉普拉斯变换的方法是密集术, 如果没有学过密集术,去搜一下泰勒公式,因为微积分的两大支柱就是泰勒级数和复列级数。 密集数是这样,它的通式是 n 乘以 xn 安从零变到无穷大穷。密集数的和就是把它们全部加起来。 这是他今天的写法,就是西格玛从零到五,从大安取整数。 等一会,我们将脱离经典的理解,换一个思路来书写他 等式。右边的总和可以写成一个函数,习惯上是 fx 这样的通用抽象函数名,但为了表达这个总和以密集数系数的一一对应关系,我们把它记为大 x。 接下来我们再做一点小小的改变,我们的目的是让这个试纸更符合计算机的符合技法,而不是用这个经典的下标 n。 我们用一个以 m 为自变量的离散函数来代替这个下标。换句话说, 这个理想函数是一个以质变量为零,一二三等等的时数函数。这本来就是系数序号的真正含义, 用计算机的符号风格来表达,他的意义是完全一样的。所以我们用小 a n 来代替下标,他仍然是在表示一个时数跟一个正着数 n 之间一一对应的关联。 好了上面的试纸,我们已经看到,我们得到了一个从小 a 函数到大 a 函数的一种映射,或者成为变换。 而且这个变换从函数体到自变量都发生了改变, 但两个函数之间却存在某种异色关系,虽然他们从名词到动词都已经不再相同, 他们却是在说同一件事情。就像我们举例说学习如逆水行舟,学习和逆水行舟的名词和动词都不一样,但却是同一件事情。 左边这个是离散函数,右边这个是连续函数。他们关联在一起,是告诉我们,这个以非负整数为自变量的离散函数,以密集诉求和函数之间存在关联。 先来看几个,大家可以理解例子,把上面的思路具象化。假设小爱这个函数是一,什么意思呢? 函数是个动词,代表的是动作,说函数动作的结果是一, 就是这个动作把自变量变成一,也就是说他是长函数,无论 n 取多少,比如一、二、三, 函数生成的密集数的系数都是一。那他对应的神秘函数大 x 是什么呢? 当所有系数唯一时,密集数的表达是是 一加 x, 加 x 平方加 x 立方等等等。讲到这里,可能有同学 已经知道是啥了,答案是一减 x 分之一,但是这个答案可能是错的,或者说不太准确。为什么呢? 因为他不是对每个 x 的取值都正确,只有当 x 位于负一和正一之间时, 级数才会收敛,所以大 x 不是现在屏幕上显示的这个函数 加上绝对值小一一的地域限制才是我们要找的函数。 如果 x 大于一,会怎么样呢?函数不会收敛, 他什么都不是。再来看一个例子,假设小 a、 n 等以 n 的阶层分之一 求他对应的大 ax, 这是什么意思呢?当系数是 n 的阶层时, me 是 x 的, n 是方, 他们的核是什么呢?对了一的 x 翅膀, 而且这个答案没有定义的限制,对所有 x 都是正确的。 看完这两个例子,从某种特殊的角度来看,我们认为密集数求和的运算其实是取一个定义率 在恢复整数的离散函数并执行这个位置的过程。 从这个过程中会走出来一个连续函数,输入的变量是 n, 但输出的变量是 x, 这很自然,因为这就是密集术的定义。接下来的问题是,刚才讲的是一个离散的情况, 一个离散求和来得到这个大而函数。假设我们想使用连续求和,而不是离散求和, 我们想要连续模拟刚才的过程, 连续模拟会是什么呢?我们将用连 去值代替原来的零一二等取值。我们用一个叫 t 的连续变量来代替离散变量 n, t 的取值范围从零到正无穷,我们可以取其间的每一个时数,而不只是整数。好了,如果我们想用连续的 t, 而不是离散的 n, 我们显然无法用通常的方式对所有实数求和代替四个码。对所有实数求和的过程的是积分, 所以我们要做的是用从零到正无穷的积分替代那个西格玛, 就像从零加到无穷大的某个函数的总和一样。 现在 n 被连续 t 取代,所以小 a 这里将是 t 的函数。 那剩下的其余部分呢?我们把 x 拷贝过来, x 的上角也不再是 n, 而是 t, 因为是积分,当然还要加上 dt 最后 右边的总和。大 i 函数怎么定型?大 i 函数是 t 积分的总和,所以 不会在结果中出现的应该只有 x。 对于 x 的每个值,比如 x 等一二或者三点五等 都对应一个特定的积分,我们可以计算出来,所以右边跟原来一样还是大 x。 现在离散的密集诉求和公式已经化成了连续密集诉求和的形式了,我们可以让他保持这个样子。 但没有数学家会接受这样一个事实,工程师更没人愿意看到以 x 为底的指数项。 唯一方面的底是一。对于喜欢微分和积分的人来说,他们唯一喜欢的就是把一微分成某种东西。 所以我们将通过把 x 换成以一为敌的形式来使这个式子变得好看一点。 x 可以写成 e 的 logo x 次方,所以 x t 可以写成 e 的 logo x 次方的提示方。 我们希望能计算这个积分。很明显,我们给 x 带入一个数,他的提示方可能会趋向无穷大。例如, x 等于二十二的提示方,不太可能收敛。比如设置时的小 a, t 为常函数一,这积分肯定不会收敛,积分会发散成可怕的样子。 这里的积分只有大 x 是小一的数字时才有收敛的机会,这时指数越大密越小。 但即使如此,不恰当的积分仍然会有发散到无穷大的时候,需要谨慎对待。 不管怎样,我们真的希望 x 小一,否则的话,积分不太可能收敛。 还有, x 最好为证,否则会有麻烦。比如 x 等于负一, t 为二分之一时就出现虚数了。 我们不想出现这种情况,所以指数的底最好为正数。 为了让积分有可能收敛, x 在零到一之间。 那么 logo x 会怎样呢? logo x 会小于零,并一直为负数。 富到无穷大。 我们不喜欢上面的写法,也没有人愿意用 logax 作为变量, 所以我们把 fu logates 用小写的 s 代替 这个符号是有意义的。因为 logax 永远小于零,所以有这个符号代表 s 永远为证。 正数用起来会方便一点。我们把负号引过去变成负 s, 等于劳改克斯。 如果进行这些改变,积分方程会发生哪些变化呢?我们强调一下, 所有的这些变化都是装饰性的,是为了使符号更简洁容易。 首先,大部分人称函数不会称为小 at, 而是 ft。 然后看这个 x t 项,经过换底,他可以写成 e 的 logo, x 的次方,挂号的 t 四方, e 的 logo, x 次方, 又可以写成一的复 s 次方。 现在我们不再用 x 当变量,我们用小写的 s 来当变量。 根据指数运算规则,我们只要乘以 t 得到一的副 st 四方,把 dt 加上,即完成 成了左边的整理和装饰。 我们输入函数变成了小 ft, 所以输出函数我们用大 f。 但他现在应该是小写的 s 的横竖,因为我们把 x 换成了小写 s, 这样方程的右边也装饰完成。 如果你愿意,也可以把九式里的大 ax 改写成大 a d 的副 s 次方, 这样他的自变量也变成了 s。 没人会把一个 s 的函数保持成 a 这样的函数名。现在让我们来看看我们最终得到了什? 这个是指是指什么?我们强调过,这个东西只不过是密集术求和的连续母女。 这是理想版本。 这是通过完全自然的转变同一事物的连续版本。他从 t 的正值定义函数开始,并将其转化为 s 的函数。 这就是被人们称为拉普拉斯变坏的东西。
681锦南高研院 01:4411电学实验室
01:4411电学实验室






