正太分布可以用EXCEL模拟吗
粉丝1.1万获赞1.8万
相关视频
 02:29查看AI文稿AI文稿
02:29查看AI文稿AI文稿哈喽,大家好,这里是大表哥。呃,今天呢,同样给大家分享我们 n 开头的函数,他是叫做正太分布型的一个函数,叫做 long dist, 同样今天是我们的第一百三十五天,看一下 还是名称 normest n, o, r, m, d, i, s, t 是可以返回,就是可以计算我们指定平均值和标准偏差的一个正台分布的一个函数。然后它的语法构成非常简单,由四部分构成,看一下 部分是 x, 是一个必须填入的,它的含义是需要计算其分布的一个数值,这是我们的参数一,参数二是命,必须填入,也是我们分部的一个算数平均值。然后第三个参数呢,是我们的 standard t, v 也是必须填, 是我们分布的一个标准偏差的一个值。第四部分叫做,嗯,后面的 t 也是必须填入的,是决定我们一个函数形式的一个逻辑值。如果为处的话,我们是一个计算累计分布的一个函数。如果为 boss 是计算我们的一个概率密度的一个类型的一个函数。我们直接看一下简单的一个计算案例。 呃,我们的参数是固定好的,我们的四十二是一个计算器分布的一个数值,四十呢是我们的一个算数的一个平均值。然后一点五呢是我们的一个标准原差。我们分别将我们的 a 二, a 三, a 四带入我们的函数中,变成我们的参数一,参数二跟参数三,然后也就是我们的一个 a 六当中的一个。呃, 啊,一个内容,如果说我们的参数是此时为处的话,我们计算的是我们的累计分布的一个函数值,他返回一个结果呢是零点九零八七。如果说我们此时参数是变为 fos 的话,直接是计算的我们的一个概率密度性的一个函数的一个结果词,他返回的结果呢是零点一零九三, 这就是我们的一个 nome dist, 可以给大家给到大家处理的一个逻辑,一个算法。然后呢也非常简单,但是大家一定要记住,我们的 to 返回的条件是一个累计分布函数, foss 的话是一个概率的一个函数,这一点大家一定要记牢喽。 然后这就是我们今天罗姆迪斯特的一个入门的视频分享,嗯,我是大表哥,关注我主页还有更多数据知识哦,你都学会了吗?
102Excel数据处理大表哥 06:56
06:56 10:53查看AI文稿AI文稿
10:53查看AI文稿AI文稿买彩票,你中奖的概率大,还是你考上清华的概率大呢?今天我们就来讨论一下这个问题,那么我们首先呢,先采用一个比较简单的概率模型来讨论这个问题,买彩票中五百万的概率有多大啊?五百万, 如果我们玩双色球的话,这个概率我之前算过,这里不重新算了啊。呃,买彩票中头奖的概率一千七百七十二万分之一,那这个概率太小了,对吧?非常小,很难中啊。那么考上清华呢?有人说考清华呀,比登天还难,那还不一定是吧,咱们看一看,考清华的概率多大啊?首先我们先从全国来看, 从全国来看,每年清华呢,他是招大概三千个人,北大也差不多招三千人,考生有多少人呢?考生,比如说去年吧,九百四十二万啊,大概一千万左右,所以 你按照这个来看,你的概率多大?九百四十二万,招三千个人,那是不是就大概是一千万分之三千呢?对吧?一千万分之 三千,一千万分之三千,那么我们把这个签约掉啊,签约掉,那最后结果大概是万分之三吧。一万分之三, 一万分之三,这个概率是一千七百七十二万分之一,差多少倍?差了大概五千倍左右,对吧?所以这个概率是他的大约五千倍啊,大约五千倍, 大约五千倍,你考上清华啊,要远远比你中五百万要容易,是吧?有人说不是这个全国高考,他分省录取,每个省不一样,是咱们每个省不一样。咱们来说一说考的比较难的省,比如说河南啊,河南省人多呀,是吧?河南省招多少人 人呢?河南省啊,招一百个人,招的人不多。考生多少人呢?考生八十三万。八十三万啊,咱们来算算河南省这个能考上清华的概率都在那。就是一百除以八十三万吗?一百除以八十三万,对吧?这个数是大概一万分之一点二。 一万分之一点二什么意思啊?比刚才那个五千倍少了,但是他也小不了多少,对不对?他大概还是中五百万的概率的两千倍。 所以说呀,与你与其做梦去中五百万,你还不如好好努力考清华,这个概率要远远超过你中五百万的概率。还有人说呢,你这个算的不对,为什么不对呢?你就算投三千个名额全在我们省,我也考不上,因为我学习不好吗?学习好还是学习不好跟考试有一定的关系,但问题是呢,有的学习不好的同学,他也可能会 高水平发挥,有的学习好的同学,他有可能会发挥失误,对不对?这是存在一个统计的问题的,所以我们不如啊,再从另外一个观点,统计学来研究一下这个问题,这个模型就计划的多了啊,统计学里面最重要的一个模型叫正态分布。 正态分布?什么是正态分布呢?我们首先呢,从一个实验啊,这个叫高尔顿钉板实验来说明。这个钉板实验说明什么呢?就说啊, 他这上面有个口子,可以往下放球,然后这里有很多个钉子啊,这个钉子非常非常密集,很多个钉子球可以在这些个钉子的缝隙之间漏下来,但 这些钉子排列啊,也比较随机,球落下来的时候吧,他也是随机的啊,底下呢,有一大堆的槽,然后呢,我们就会发现,如果一个球落下来的话,他落到 什么地方不一定,他可能会落在这,也可能会落在这,也可能落在这。但是如果你大量的球一次一次的往下掉,或者一次掉下来很多球,你就会发现呢,中间这个地方的球特别多,两侧的球比较的少,再往下就更少,再往下就更少,他会形成一个曲线, 大概是这个样子啊,人们经过研究发现这个曲线呢,非常接近于一种特定的形状,这个形状就叫正态分布。其 其实不仅仅是这个问题正态分布,人们发现呢,只要一个问题中涉及到很多个随机量,那么这个分布加起来就非常接近正态分布。 什么动式接近随机量呢?举个例子,身高就是这样,我们想统计啊,比如一个国家啊,某一个年龄段的人,他的身高有多大?发现有的高,有的矮,但是最终的结果是大家都集中在某个范围内啊,有一个 身高的人是最多的,那么高的和矮的都比较少,也就接近于正态分布,对不对?身高是比较接近的,但是也有一些不接近正态分布。举个例子,收入啊,比如说香港地区,我们统计香港地区人均收入啊,这个是人数, 这个是收入啊,这个是收入。我们发现什么呢?是香港地区吧,低收入的人非常非常多,然后呢就开始降,降到了一定程度之后,到了高收入人群又突然多了一下啊,可能没有这么高啊,话有点高了,也就是说在香港地区呢,贫穷的人特别多,他有钱的人也特别多,中间反而少, 为什么会出现这种现象呢?这叫马太效应啊。以后我们会讲这个问题,也就是说有一些分布他是不符合正态分布的,但只要这个问题是随机的,很多时候都是符合正态分布的。那咱们就可以假设,假如你在考试过程中有很多的不不确定因素,比如说呢, 可能你的知识点有一些漏洞,但这些漏洞是随机分布的,那么有可能考了这些漏洞你就考的不好,也有可能没考这些漏洞你就考得好。所以我们可以假设你的成绩是正态分布的啊,你每考一次成绩都正态分布。如果按照这种办法,我们就可以知道你考上清华的概率是多大了。为了计算这个问题呢,我们首先需要知道正态分布的一些基本 基本的数学内涵。纵坐标是概率,其实不是概率,叫概率密度啊,但是他基本上跟概率的意思差不多,概率密度啊,横坐标呢,是他的数值, 数值啊,一个正态分布函数,他最中间概率最大的这个位置叫期望,其实就是平均值啊,平均值。同时呢,他还有一个量,叫做这个方差和标准差,这个方差和标准差呢, 表示了这个叫平均值。方差和标准差呢,表示了你这个幅度宽不宽。比如说我们画了这么一个图啊,然后我们再画这么一个图,那么很显然这个图啊,他比较集中,这就叫啊,这就叫标准差小, 标准差七个码比较小,而这个就叫七个码比较大啊,就叫七个码比较大,然后我们想计算呢,你最后我知道你这个概率情况了,我想计算你分布在某个区间的概率多大,怎么计算呢?我们在这里啊,做一个线, 比如说我就想计算一下啊,从你这个平均值到平均值加标准差之间啊,这个叫喵加西个吗?叫平均值加标准差,在这个范围内你出现的概率有多大?那么就是底下的这个面积啊,就是这个的面积, 而且我们会发现,因为你最后的考试成绩一定在这个里面啊,所以说呢,整个这个图像下方的面积是一对吧?啊,在这里面的概率啊,如果是百分之五十的话,那我就告诉你,你出成绩出现在这个范围内的概率是百分之五十。人们经过计算呢,得出了一些基本的结论啊,比如说一个随机量,这个随机量的取值在 啊,平均值减一个七个码,和平均值加一个七个码之间,平均值加标准差之间,他这个出现的概率是百分之六十八点三啊, 在平均值减两个七个码,到平均值加两个七个码之间,他的概率是百分之九十五点四, 百分之九十五点四啊,等等等等,我们就不再往下写了。也就是说,假如说你可以把你的考试成绩统计出来,你就可以利用高斯分布这种方法, 知道你最终的考试成绩在一定范围内的概率了。那我们举个例子吧,比如说啊,有一位同学叫小明,这个小明同学啊,他在参加模拟考试,或者是在高三的几次考试中,他的成绩如下分布啊,他第一次考了五百八十分 啊,第二次考了六百分,第三次考了六百八十分,第四次考了六百二十分啊,假如说他有四次考试成绩是这样的,清华的分数线多少呢?清华啊,六百九十分。 哎呀,他一看完了,我肯定考不上。为什么呢?你看你看,我这就五百八,我就从来没考过清华分数线呢,对吧?清华分数线可能是六百九啊,基本都稳定了。那我现在这个分数不够对不对啊? 我再怎么抄,水平发挥也没用,我最好的一次还差了十分,小明同学是不是一定考不上呢?不是的,他其实还是有希望的,我们要计算一下他的均值是多少。首先说均值, 均值很简单,就是 n 分之一倍的西个马 x 二,就是你把所有的数值给我加起来,加起来就是除以它的数就行了,也就是五百八加六百加六百八加六百二,再除以四,这就可以了。那 这个数得几呢?这个数得六百二十分,也就是他的期望是六百二,但他不是说一定会考六百二,他还有一个标准差七个吗? 七个马的算法就比较复杂了,他等于 n 分之一的每一个数据减去平均值的平方,再开根号。 你也不用管这啥意思,反正大概就是说吧,你用五百八减六百二,减完了就一平方,然后再加上六百。啊,我忘了写七个码了,还有 加个星吗?再加上六百减六百二啊。把它给平方,再加上六百八,减六百二,再平方,再加六百二减六百二,再平方。平方完了之后求和,求完了和再除以四就行了。你把这个数算 出来啊,计算器其实可以直接帮你算出来的啊,这个数呢,大概是三十七点四,三十七点四。好了,我们已经知道了你的平均值和你的标准差了,现在我就想问你跟清华的分数线差了几个标准差呢?清华是六百九,对不对?你呢?是六百二,所以平均值是六百二,所以呢,你差了一个数 就是七十分,那么这个七十分相当于几个膝盖吗?呢?啊?相当于一点八七个标准叉膝盖吗?啊?也就是说啊,我们要画出一个正态分布曲线来啊,这个正态分布我在这画吧,没有地方了,我在这画啊, 这个是你的概率,这个是你的分数啊,画出一个正态分布曲线来,这个正态分布曲线呢?他的均值就是六百二十分啊,我希望你能够考 六百九十分,中间这个差别我经过计算是一点八七个标准差,那么我这回就可以查表了,表会告诉我,这个地方你要考上清华,你必须得比一个分数高,对吧?所以这个部分的面积就是你考上清华的概率, 我们可以算一下。那么这个计算呢,是通过查表完成的,表会告诉你到底有多大,这个数值结论是大概百分之一点五, 也就是说你还有百分之一点五的概率上清华,你说我就考四百分,我每次都四百分以下,我能不能上清华,你去算一下,你也会有一个概率,只不过可能是万分之几量级的,对吧?也是有一定概率的啊,你可能会超水平发挥,对吧?但不管怎么样,他都比这个一千七百七十二万分之一要大的多,对不对? 所以希望大家每一个人呢,都对自己有信心,因为从统计上讲呢,每一个人都有可能会超水平,超水平发挥,只要你相信自己啊,一切奇迹都有可能会发生。
3.9万李永乐老师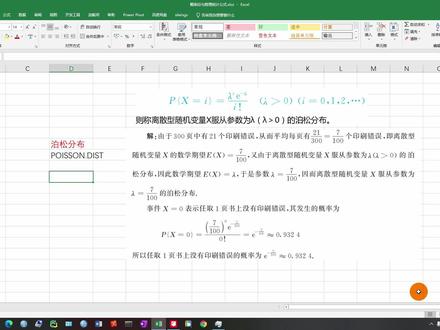 03:20查看AI文稿AI文稿
03:20查看AI文稿AI文稿博松分布,他的概率在也是有种的计算,嗯,先看一下他的定义,这个是他的概率公式,就是他发生哀赐他的 概率,然后中间有一个参数囊大,囊大的话,他的取值就是他的期望或者是他的方差, 然后在 excel 里计算的话,他共是用的是这个,等于 我们看到这有三个参数,第一个就是他发生的次数,比如说他这个要计算他不发生错误的概率的话,他的次数就是零。然后第二个参数命命的话, 就是他的希望就是这个公式里的能量,所以是零点零七, 因为我们是要计算出现零次的错误,所以应该这个参数应该是零。如果说我们要计算,比如说小于 两次的概率,那这个地方这个参数就应该写一,但是因为我们是计算零次,所以呢这个地方参数是零, 然后他的概率就是零点九三。之前讲的二项分布的话,当他试验的次数很大,比如说超过一百次,然后呢他发生的概率又很小,比如说小于零 点一的时候,就可以用泊松分布去见四计算二项分布,因为二项分布当他试验次数非常大的时候,他计算出来的这个排列他的数字是非常大的, 就不利于计算。所以呢可以用泊松分布去近视计算二项分布, 然后指数分布,指数分布,他的概率的公式是那么大,乘以 e 的负那么大 x 次方, 他主要用在就是电子元件的寿命以及随机服务系统中的服务时间,然后他的那个期望的话,是等于那么大分之一,然后方差是 囊的品方分之一, 然后看这个例子,在一个 ceo 中的计算的话,他的公式用的是 bxpon 两件 st, 然后 x, 比如说像这个 一只狼大等于零点一,然后要计算他小于等于二十次的概率,然后这个 x 的话他就是二十,狼大的话是等于零点一,因为他这是要计算小于等于二十次,就是 需要这个参数的话,就需要用哪击分布函数,这个地方可以选数,也可以选,也可以写一。
74苹 28:55
28:55 07:41查看AI文稿AI文稿
07:41查看AI文稿AI文稿判断一组数据是否是正态分布,是否是有偏差, x 里面的描述数据分析统计工具帮到你 一份成绩表,考了三门课程,把数学、计算机原理跟法学概论,那么现在我要看一下这三门考试成绩 是否符合规范,有没有需要改进的差异。那么我如果只是看上面这么多的数据呢,我是完全看不出来的,那这个时候呢,我们只需要借助 x 要提供的数据分析工具就可以了,大家注意哈,我需要点击的是这边有一个数据分析按钮, 当我们去点击数据分析之后啊,我们对他进行描述统计,那这里面就会把平均指杀方差呀啊,最大最小啊,全部都给你计算出来。然后这个时候呢,我们注意输入的区域呢,一定要从 c 一开始 拖动到最后一个单元格,当然你不想拖的话呢,你可以直接去输入后面的数据,比如说有五百条记录,你把后面的五十五改成五百就可以了。那么分组方式呢,是 x 要自动识别的,我们就不需要变, 然后标志位于第一第一行或者第一列啊,这个时候呢,他会自动的进行识别,我们也不需要管他。那么输出的区域在哪里呢?我们在这里随便选一个啊,比如说输出的区域,我们把这边删掉,原来默认的给他选一个机,好 放大一点,大家看的清楚一点,对于汇总统计的话,就是我们要把结果汇总出来,平均的知心度呢,我们一般放到百分之九十五 啊,也说显著百分之五的他是不统计的。那么 d k 的最大值跟 k 最小值呢?如果你勾选的话,你在 在里面去输一和二啊,比如说我就要最大跟最小,那么就默认就行了,就是在这里默认,你看一下,就是一啊,就最大的跟最小的也要统计出来。那么设置完成以后啊,大家注意啊,点击确定啊,一定要点击确定一下啊,这个地方要勾一下,然后点击确定。 好,那这个时候呢,他就生成了一个表格,大家注意啊,对,这个表格呢,我们要给他添加一个 设计啊,给他加一个样式啊,比如说,呃,最简单的,我给他添加在这个踏入里面呢,给他变成表格样式,这样呢,看的比较清晰明了一点啊, 等一下倒退,我这样把它重新选中一下,把这些数据选中一下,然后在插入中呢,给 选择一个表格,包含标题就可以了。好,那这个时候呢,我们注意哈,对于不需要的这个数据的区域,我们可以选择删除啊,列一列,他默认的,我们可以把它给删掉啊,如果删不掉的话,我们也给他给他改成数据就可以了。这个列一的话,就是具体的数据 啊,结果吧,这个地方可以理解为是结果二 啊,就是这边可以理解为数学的结果啊,计算器的结果结果二, 那这个地方是法学的结果,那我在这里呢给他定位为结果三省市啊,你可以理解为是法学结果三啊。 好,那么在这里我们能看到什么呢?比如说,哎,平均值啊,这个高等数学的平均值呢?是七十八分,对吧?这里有个标准的误差 啊,一点五减啊,标准无差,这个就是差多少啊,这个你会发现数据稍微多一点啊, 重数啊,最多最多的就是大众化的,考了八十三左右,中位数呢,就是这个数据的最高,这跟最低值之间的中间那个数,比如说一到五三就是中位数啊,中位数七十九,我们会发现啊,中位数非常接近于平均值,看到了吗? 这个也是几乎接近的,但是你会发现法学呢?法学这边是九十二、九十五啊,他比较不接近啊,然后你会发现重数是九十五,也就说大部分的人考到了九十五分,但他平均值就是 九十二,这说明有一部分人的成绩是比较低的,但大部分的成绩很高,对吧?怎么看出来呢?来,你这个这个标准差,标准差值多少?这里是有,我们来看这里有一个 这个偏度啊,偏度呢,这个很重要,就是他往哪边偏,如点这个地方偏零点三六,零点零三,这个地方你看注意啊,负一点一,那这个偏度就非常大。 那么再往下我们来看,最小四十八,最高一百,这边最小八十五,最大值九十五。那么我在这里我们能够看到一个什么呢?就是说 这个数学跟计算机的成绩啊,他相对来讲比较正常。比如说,呃,就是平均数跟 重数挨着很近,就说大部分的成绩呢,就是跟平均值是挨着的啊,他是个正态的曲线啊,什么意思?比如我们给你画一个,这他是他是这么一个分布模式,他不偏啊,比如说,哎,大部分人是 在这一块了,哎,只有少部分的最高值跟少部分的最小值,那这叫做正太分布, 但你会发现这个的话,他就比较偏了啊,就说他最大值九十五分,最小值八十五分,而他的这个平均值达到了九十二分,而且他的偏斜度达到了一点幺幺八啊。那么在这里呢,我们就可以做一个判断,就是他的这个成绩啊,有点偏高了 啊,他他偏了,他不是说啊,有高的有低的,那他整体有点偏高,比如说他这个曲线呢,如果 你把它画的话,他可以理解为这就是倾斜的,这边怕就突然下去了,就是大部分的人太高了,就像我们现在的贫富分化一样,太大部分人都很富化,一部分人很穷, 这样的话就会导致贫富分化很严重啊,这个道理是相同的,这个地方叫做偏斜度啊,偏斜度他往哪边偏啊?他这个正态他是偏向一侧啊,也叫做这个聚集程度吧 啊,那个这平均值跟平均值挨着比较近的,就是积攒程度啊,靠,靠不靠平均值啊?你看大部分的数,重数零八十三,靠平均值的啊, 七十九分,中位数啊,中位数中间的数跟平均值挨着很近啊。所以呢,从这里我们就看到啊,就数学跟总结一下,数学跟计算机相对比较正常,而法学呢,他这个,呃,有点偏高了, 整体分数有点偏高,也就说你可能你的出题的难度太低了,你可以这么去理解啊,但是如果你只是看这边的话,哎,这不好分析啊,因为数据太多了,那么在这里呢,他给到了我们一个比较准确的测量结果啊, 再次解释一下,中位数啊,就中间数可以理解,中数就是最多的数,偏度叫偏斜度啊,风度啊,就高峰的那个那个度数啊,这个就与那个曲线有关系啊,最大值、最小值。这个其实我没多 都很熟悉的,是吧?求和是多少?总共总共的合计数嘛?啊?你这个样本数是五十四个数啊,他致信度九十五,按要求来做的啊, 比如说这个可信度是比较高的。好,那么这就是关于数据分析的一个描述,数据分析的应用。
477明宇电脑培训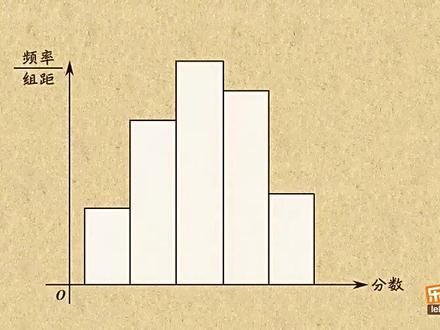 02:38查看AI文稿AI文稿
02:38查看AI文稿AI文稿这里是五十名学生某次考试的成绩,仔细观察一下,不难发现,这里分数超过九十分的同学不多,只有这六个。分数低于六十分的同学也不多,只有这五个。大部分同学的分数都集中在七八十分。咱把这些分数按组分好之后,画成一个频率分布直方图,就是这样, 如果组距越来越小,分组就会越来越细,那这个直方图上的这线也就越平缓。如果把这个图中的每一个分数堪称随机变量 x, 那 那这条曲线就通常被称为概率密度曲线了。而像这里这样形状类似一个大众的曲线,那你当然可以叫他中性曲线,不过这样太 low 了。他还有个高大上的名字,就叫正态曲线,而符合这种正态曲线的分布就叫正态分布了。 发现美正泰曲线两头低,中间高,左右对称,并且曲线和横轴之间所围成的面积横等于一,因为这面积就是所有概率的和,那他们加起来肯定 十一了。这些都是从图形的形式上分析出来的,那接下来咱就从严格的数学表白式上再来分析一下这个曲线。他的解析是就是这样,别看他长得很复杂,代为师给你分析分析就不这么可怕了。这里的派和异是俩常数,也就是你熟悉的自然对数和圆周率。 而这里的西格马和喵是两个参数,其中这个喵是数学期望,而西格马是标准差。把这俩参数写在括号里,前面再加个 n, 用这个东西就可以表示正态分布了。 以后你再见到他,那你就要想到这玩意表示的就是正态分布,而这里面俩参数的数值会影响整个曲线的位置和形状。比如刚才这个曲线的西格马就等于一,妞也等于一,那这里对阵轴恰好也是一。 如果七个马不变,喵却变成负义了,那这个曲线就长成这样,其中对称轴就是负义。而这回让喵等于零,那这个曲线就跑到歪手这来了。不难发现, 喵的取值恰好是曲线对称轴的位置,喵是几,对称轴就是几。而如果让这个曲线的另一个参数,也就是这个西格马变一变,比如当他等于零点五时, 那这个曲线就变成这样,而当他等于二时,这条曲线就变成了这样。很明显,他越大,曲线就越矮胖,反过来他越小的话,那曲线就越高瘦。而这三条曲线其实都有点特殊,因为他们三个都没有,都是零,所以他们都关于外轴对称。那咱就给这类曲线起个新名字,就叫标准侦探曲线。 以后再看到这个名字,你就得立马想到他其实在告诉你,这里的没有等于零,或者这条曲线是关于歪州对称的。 ok, 总结一下,所谓概率密度曲线,就是反映了随机变量概率分布的图像, 而长成中型的概率密度曲线就叫正态曲线了。如果他还关于外周对称,那他就叫标准正态曲线。至于他的解析是吗?最重要的就是西格马和喵这俩参数,其中喵决定了对称轴的位置,而西格马决定了曲线的高矮胖瘦。怎么样?听懂了吧?赶紧动手试试吧!
7984数学王子特训营 01:23查看AI文稿AI文稿
01:23查看AI文稿AI文稿今天我们来学习如何使用数据透视表来计算分数的分布,之前我们用 frienc 和康定排数都做过类似的演示,然后选中数据,单击插入数据透视表表格和区域,然后保存在现有工作表,单击确定, 然后我们将成绩拖入行的区域内,然后将学生也拖入到行的区域内,然后再次将语文成绩作为作为直,然后拖入到直的区域内。这里呢?单击求和项,然后选择直自断设置这里由求和改为技术, 并且在子单机行标签右键单机,然后这里选择组合。这里我们起始于零,因为考试就是零到一百分,然后不常为时,正题不变,我们可以非常轻松的统计出 当前学生然后的那个成绩分布。我们选中当前区域,然后直接单击插入数据的后视图,然后选一个扁状图。那我们可以先把这里头先先折叠吧, 选中折叠后的区域,然后单击插入数据图数透视图,然后选一个扁状图,我们就可以非常清晰要看到当前学生的一个分布状态。好的,今天的分享就到这里了,再见。
152火车爸爸带你玩表格 13:34查看AI文稿AI文稿
13:34查看AI文稿AI文稿要统计学入门,就必须先了解正态分布。正态分布是最重要的一个分布,也是统计学的基础。正态分布曲线是自然规律的一种呈现, 在对大量的随机事件进行统计后,发现正态分布曲线往往是必然的一种结果。正态分布曲线呈现一种铃铛形状,英语里叫 bell shipped curve。 这个公式是正态分布曲线的概率密度函数。大家不用害怕,本节课不要求大家掌握这个公式,本课程系列只对公式中几个参数的含义进行感性理解。 我们看到公式里有一个派,圆周率。你也许感到奇怪,正太曲线里没有圆弧或圆形啊,怎么会出来个派呢?这个问题我也回答不了,我只能说这就是数学的神秘之处, 也是发现这些公式的数学家的伟大之处。我们向那些骨灰级的数学家们致敬。 发现正泰分布公式的数学家是德国的高斯,所以正泰分布也叫高斯分布。高斯对正泰分布的应用与发现做出了人类发展史上最伟大的贡献。 这张图片是德国某个版本的史马克纸币中的高斯化背景,里面还有正太分布曲线和概率密度公式。 我们讲统计,也就肯定讲到概率。提到概率,大家肯定想到抛硬币。大家写英语作文时肯定都背过 every coin has two sides 这么一个陈词滥调。 抛一枚均匀的硬币,得到正反面的概率都是百分之五十。那么抛硬币与正态分布有什么关系呢?假设我们抛 同一枚均匀硬币,得到正面,我们用空心圆圈表示。得到反面,用实心圆圈表示。我们可能得到这么一个结果,共有六次正面,四次反面。我们把这抛十次硬币这样一件事,即为第一组实验。 我们再抛十次同一枚硬币,即为第二组实验,得到七次正面,三次反面。 假如我们进行了一百组这样的实验,得到一百个结果,我们把一百个结果中得到的正面数量都记下来,分别为七、九、四、七等等,共一百个数据。这一百个数据的取值范围是零到十的整数。 现在我们把这一百个整松的零到十出现了次数,用坐标轴上的柱状图来表示,正面次数零出现了零次, 所以什么都不画正面。次数一出现了一次,于是在坐标轴一这个位置画一个高度为一的柱状图,次数二出现了六次,就在坐标轴二这个位置画一个高度为六的柱状图,依次类推。 柱状图画完后,只出现一次正面的概率是百分之一,出现两次正面的概率是百分之六,三次正面的概率是百分之十二,四次正面的概率是百分之二十三,以此类推。然后我们发现这个柱状图的轮廓正是一个正态分布曲线。 实际上,在概率统计学中,抛十次同一枚硬币的实验,叫做十重伯努力实验。我们进行了一百组这样的实验,可以称为一百次十重伯努力实验。数学定理表明,大量的恩重伯努力实验的 结果就能够产生正态曲线。恩宠不努力实验这个概念不要求大家掌握,因为读起来和理解起来都比较拗口。但大家既然学了这门课,知道这个概念还是有好处。 以后有人跟你聊抛硬币时,你可以说,嗯,同级学上这个叫恩宠不努力实验,这样显得比较专业。 事实上,可以用更简易的一种方式来进行恩宠不努力抛硬币实验。假设有一颗均匀光滑的圆形豆子和一只均匀光滑的圆形钉子,豆子落在钉子中间后,会向左或向右落下左右概率都是百分之五十。 那么一个豆子落下,就可以看做抛了一次硬币,豆子向左或向右,就可以看做硬币的正面或反面朝上。假设我们有食行钉子,然后放落一颗豆子,豆子下落碰到 每一个钉子向左向右的概率都是零点五。十行钉子下面有十一个槽子,我们可以根据豆子落入哪个槽子来推断豆子经过十行钉子时几次向左,几次向右。例如, 假如一颗豆子落入中间槽子,那么这颗豆子肯定是五次向左,五次向右。假设向左代表抛硬币得到正面,向右代表抛硬币得到反面。如果一颗豆子经过适行钉子落入最左边第一个槽子, 我们可以看做抛了十次硬币,共出现了十次正面。假如落入第二个槽子,则共出现九次正面,一次反面,一次。类推,假如落入最右边的槽子,则出现了十次反面。下面我们用虚拟仿真程序来做这个实验,我们设定十行钉子落下一百颗豆子, 随着越来越多的豆子落下,槽子中的豆子逐渐呈现一个轮廓,这相当于做了一百次十重不努力抛硬币实验。槽子中的豆子轮廓正是一条正态分布曲线,和我们抛硬币得到的结果是一样的。这种豆子和钉子的实验叫做加尔顿板实验。 加尔顿板可以演示在看似混乱的随机现象中存在的规律,这个规律就是正态分布。顾名思义,加尔顿板是加尔顿发明的。 嘉尔顿是英国维多利亚时代的统计学家、博学家、社会学家、心理学家、人类学家、热带探险家、地理学家、发明家、七项学家、遗传学家和心理测量学家。他是最早提出通过指纹来鉴定个人身份的研究人员之一。报个料,他还是英国生物学家查尔斯达尔 轮的表哥。现在我们反过来看,这个轮廓虽然大致为正太曲线,但曲线的光滑度不高。这是因为我们只放了一百个豆子,规律表现的还不够明显。下面我们放一千颗豆子重新做一下这个实验,可以看到,从一百颗豆子到一千颗豆子, 正态曲线的光滑度提高了。这说明重复实验次数越多,我们观察到的规律性就越明显。 下面我们改变一下实验参数,我们把钉子行数记做 n。 刚才的实验是 n 等于十,十行钉子,现在改成 n 等于二十行钉子,再放一千个豆子落下来观察结果, 结果显示仍然是一条光滑的正台分布曲线。我们比较 n 等于十和 n 等于二十的曲线,发现 n 等于二十的曲线比 n 等于十 曲线要扁一点。这个结果也是可以直观理解的,钉子越多,豆子可以落下的岔路就越多,底下的槽子也越多,豆子必然更分散。 事实上,丁字行数 n 越大,正态分布的曲线就越扁,正态分布的方叉就越大。 n 越小,豆子越集中,正态分布的曲线就越窄,正态分布的方叉就越小, 方叉就是概率密度函数中 c 哥们的平方。关于方叉的概念,本课只做题集,后续课程会详细展开。 例如这个图中有四条正态分布曲线,蓝色曲线的方叉为零点二,方叉最小,所以蓝色曲线最尖。黄色曲线的方叉为五点零,方叉最大,所以黄色曲线最扁。到目前为止,大家可能觉得 杰克的内容没有什么意思,因为所有结果现象都是很直观的。再例如,豆子落下形成的正太分布曲线是对称的,对称轴就是最中间的那个槽子,这也是直观的,因为豆子向左向右落下的概率都是一半一半,肯定是对称的嘛。 下面我们再改变一下实验参数,来做一次加尔顿板试验,看是否会让你觉得神奇。我们仍然放二十行钉子,一千颗豆子,只不过我们把每行钉子向左向右的概率改成随机。 例如这一行钉子向左的概率是零点九四,向右的概率是零点零六,这一行向左的概率是零点五八,向右的概率是零点四二。每一行钉子向左向右的概率都是随机生成的。那么豆子下落后形成的轮廓是什么样的呢?在我上学期 板上,有的同学猜可能是一条比较平坦的一字型轮廓,有的同学猜可能是一条像股市大盘一样的参差不齐的曲线。 下面我们开始实验看一下结果可以看出,除了对称轴不在中间,草字豆子轮廓仍然是一条光滑的正态分布曲线。大家有没有感到有点神奇呢? 我们重复四次上述实验,每一次都是二十行钉子,一千个豆子,每一次每行钉子向左向右的概率都是重新随机设定的。 四次实验结果显示,斗字的轮廓都是光滑的正太分布曲线,只是曲线对称轴的位置有所不同。事实上,每次重新设定每行钉子的随机概率并且确定不变后,对称轴的位置是可以根据各行钉子的概率计算出来的。这个对称轴的值 就是概率密度函数中的 miu。 这个图中有四条正态分布曲线,有三条曲线的 miu 相同,所以对称轴也相同。只有一条绿色的 miu 不同,所以对称轴也不同。在本节课我们也不对缪做详细展开, 下面我们给出中心极限定理,非严格数学意义上的一个版本,方便大家感性理解。其数学表数为所研究的随机变量,如果是由大量独立的随机变量相加而成,那么他的分布将近似于正态分布。 其通俗表述为,如果一个结果是有大量的不相干的因素累加导致的,那么这个结果一定表现为正态分布。例如,某个省某年的高考,全部考生的英语成绩卷面原始分必定服从正态分布。下面我们来分 学习一下英语高考的成绩分布。一个考生的高考英语成绩其实受到了无数因素的影响,每一个因素都可能使最终英语分数更高一点或者更低一点。例如,性别、 出生地、教育水平是否上过幼儿英语,小学英语老师水平、中学老师水平、英语老师性格是否喜欢英语电影、接触外国人频率、 饮食营养、高考当天天气、高考当天健康水平、高考当天心情等等等等。有无数的表面上相关的或者不相关的因素, 我们无法证明每个因素对英语成绩的影响到底有多大。但遗憾的是,我们也无法证明每个因素与英语成绩无关,这也就是一些社会培训机构向家长贩卖焦虑的原因。每个因素对成绩所产生的影响, 就好比一颗豆子经过一颗钉子时,向左向右的概率说不清楚,但这个概率一般不会是左右各零点五。这个因素总能使分数更高一点或更低一点。我们把豆子向左表示为分数更高一点,向右表示分数更低一点。 一名考生从小到大的生活历程,包含了无数因素的影响,最终得到了一个高考英语成绩相当于一颗豆子经历了无数行钉子的下落,最终尘埃落定,落到槽子里。 某省某年,数十万计考生最后的成绩分布相当于数十万个豆子经过了无数行钉子落到槽子里。根据中心极限定理,其分布必然是正态分布。 现于程序页面的篇幅,我们只进行了三千颗豆子,一百行丁字的实验,结果可以看出,豆子轮廓是正态分布曲线。 上述的高考成绩的例子只是现实世界中无数例子中的一个。只要参加高考的人足够多,所有人的原始分数必然是正态分布,考最高分的人和考最低分的人必然都只占少数, 都分布在曲线两边的尾巴上,而大多数人必然都是在中间位置考一个不高不低的分数。 所谓中庸者,不偏不倚,无过不敌,而平常治理乃天命所当然。这里我们提一下相关的历史时期和人物, 我们的历史和文化都必须由我们炎黄子孙来背负,传承、发展与弘扬,此处不做展开讨论,但每个同学都应当认真死。最后,我们来说一下,一个人的分数若落在双边的尾巴上,那必然是一个小概率事件,因为一颗豆子 要想从一开始一路向左或一路向右落到草字里太难了,所以最两边的草字里几乎没有豆子落进去的。一个人的分数 若能够落在正太分布曲线双边的尾巴上,无论是考的太好或是考的太差,都是具有极端显著性的情形,必然引起人们的关注与研究。 你看,每年的高考状元都要上头条新闻,人们会研究他们的学习方法,每年落榜的都会经历无数次的来自内心和来自别人的心灵考,但这其实都是注定的,有人就有竞争,有竞争就有江湖,有江湖就有正态分布。 现在所谓的内卷不就是人为的来画一条正态分布曲线吗?抱歉,话又讲多了,下一节课我们将从中心极限定理的另外一个 通俗版本均值抽样,来研究正态分布和双边尾巴的极端情形。我们将这样一步一步的带大家走到体检验的面前,后续课程敬请期待,谢谢大家!
2443Teacher大猫咪 00:58查看AI文稿AI文稿
00:58查看AI文稿AI文稿这个是也是正态分布的,咱们天天给学生考试是吧?啊?那个成绩要正态分布,这个正态分布怎么样?大致的。 哎呦,这好玩,这就是个正态分布,你看它实际上是这样的,就是你一个猪从中间上落下来,然后经过大量的随机碰撞,那么落在这的概率最高,但是并不会勾过来的,就会有落在其他地方的可能性。 然后我现在把它堵着,然后我一次只放下来一个,那么每一次这个道路在哪?你是你是不知道,你是没有办法登记, 然后每次扔下来一个都不一定传过来。所以这个统计规律只有在大量随机事件同时发生,或者随机事件反复发生的时候才会有意义。
16.4万反面教材 01:36查看AI文稿AI文稿
01:36查看AI文稿AI文稿教你轻松演绎正太音哎,哥哥姐姐我好喜欢你们呀,这么可爱的正太音有没有很喜欢呢?那下面教你轻松演绎正太音。 首先啊,我们还是要找到发声的位置,那结合之前我分享的十字巡声法是在高且靠后的位置,那我们先发啊,来找一下声线位置啊啊啊啊 哦,然后先普通的读一遍,小姐姐我好喜欢你啊。然后我们先加入内心戏,然后来一个可爱的,要那种软软糯糯感觉的 小姐姐可不可以帮帮我?然后高冷感觉的要像一个不苟言笑的小大人一样,哼,走开,我不需要。然后接下来是 活泼的,就是感觉那种阳光爽朗有活力的感觉。哇,今天的天气可真好。然后还有就是讨厌的熊孩子,那么我们接触过熊孩子的人应该都懂那种感觉啊,就是那种欠欠的那种, 嘿嘿,我就欺负你了怎么样?然后还有胖嘟嘟肉乎乎的小男孩, 嗯,我感觉没有吃饱还能再吃个鸡腿,是不是很好玩呢? 我们每个人啊,都会有丰富的内心活动,我们就是要把对应的情感带入精心演绎就可以了,这样就能使整个角色鲜活起来。那么大家点赞收藏,多多练习一下,明天我将跟大家分享一下萝莉音的演绎。那今天的正太音你学会了吗?拜拜。
1828尹小胖儿 13:45查看AI文稿AI文稿
13:45查看AI文稿AI文稿这个视频我们来讲一下正态分布,那么首先我们来梳理一下知识点啊,第一个正态 曲线啊,这叫正太密度曲线,那它是一个函数啊,这个函数的图像,这函数呢,是这样的 啊,这样的函数,那我们如果随机变量,他的概率,他的概率分布,密度函数呢?是这样一个函数的话,我们就说这个随机变量是服从正态分布的 啊,正态分布,我们记住啊, x 服从这个 n, 我们用 n 表示啊, 前面我们二项分布呢,用 b 表示二项分布,那么这个正在分布,我们用 n, n 表示。这个 mill, c 个码的平方啊,这样来表示。这个 mill 呢是 mill 为均值或者数学期望啊, c 个码的平方是方叉 啊,方叉,那什么是标准正态分布呢?标准正态分布, 那么也就是这个随机变量呢,满足这种 n 零一,那么也就是这个正在分布。这个六呢,等于零,那么 c 个码呢,是等于一的 啊,这个是叫标准正态分布啊,我们看一下正态曲线的性质, 正态曲线的性质,那我们画先画一个图啊,我们的符合正态分布,那么正态曲线它是长什么样子呢? 就是长这样的样子,像一个富士山一样的山包啊,山包他有哪些性质呢?首先第一个啊,这个曲线呢,是位于 x 轴,这是 x 轴的上方的啊,位于 x 轴上方 啊,与 x 轴不相交啊,这是第一个。第二个呢,他是单封的啊,他图像是单封的啊,然后是关于 x 等于六对称的啊,对 成轴是 x 等于六啊,关于 x 等于六是对称的啊,这个六呢,是它是均值。第三个性质,那么就是当 x 等于 miu 的时候 啊,他们取峰值点,也就是取到峰值,这个值呢, x 等于六,那六减六是零了,那么 e 的这个这坨就等于一,那也就是他的峰值呢?嗯,也就是在 x 等于六处啊,达到峰值, 达到峰值,峰值呢,就等于,呃, c 个码乘以根好像二派分之一, 那么第四个性质,那么就是这个富士山啊,这这个曲线和 x 轴的组成的面积是一 啊,他们的面积是一,第四,第五,第五呢,就是当 c 个码一定时,也就是他的标准差异定时,呃,那位置呢?这个曲线的位置是由这个均值六来决定的啊,由六 确定啊,也没有确定,那么随着 mew 的变化呢,是沿着 x 轴移动的啊,平移的,平移的。那么第六个,那就是当 没有确定了啊,没有一定时,那也就是他说对称轴定死了,定死了以后,那这个形状呢?就有曲线的形状,由 c 个码确定啊, c 个码确定,那么怎么来确定呢?那就 是,嗯,第一个,就是当四个码越小的时候啊,越小,那么这个曲线的形状呢?曲线是越 越小,那么这个值,这个峰值越大越高,那么就是越瘦高啊,越瘦高,形状越瘦高,然后 c 个码越大, 那曲线呢?是越矮胖啊,我们叫矮胖, 矮胖,那么他的图像呢?我们画画两条这样的,这样的图像,我们以 xx 六等于零为例啊,那你看啊,这是一个 曲线,那这个曲线呢啊,这个就是 miu 等于零点五的情况啊,那这个曲线, 那这个就是没有等于一的情况,就是没有等于零点五啊,越小的话越瘦高啊,大的啊,没有越大,他反而是越矮胖啊,越矮胖,这, 这是他性质啊,六个性质,那么我们看最后一个知识点呢,就是三四个马原则啊。什么是三四个马原则? 那我们三四个码原则呢?就是他这个 x 大于等于六,减去 c 个码,然后小于等于六,加上 c 个码呢,这个概率是一定的啊,不管你,你只要是正态分布啊,你这个随机变量符合某个正态分布,那么它的概率是定死的,约等于零点六八二七啊,那 这样一个区间呢?二字二倍的 c 个码,这样的区间, 那他也是概率是定死的,就是约等于零点九五四五, 那么三十一个码啊,没有减去三十一个码啊,然后 x 小于六,加上三十一个码,那么这个区间也是定时的,零点九九,这个概率就比较大了。零点九九七三,哎,我们发现这个, 这个在三 c 个嘛,这个区间以外的,他的概率呢?大概一减就个零点九九七三,就是零点零零二七,这概率非常小啊,所以说我们在在实际应中啊,我们在实际 应用中啊,随机变量,这个 x 是符合正态分布的啊,那我们通常认为 x 只取啊,啊,通常认为啊,我们是通常啊,通常认为,那么 x 只取这个三 c 个码,这个区间就是六,减去三 c 个码到六,加上三 c 个码,这个区间内的 值啊,只取他的值,那剩下的之外的呢?由于概率非常小,那我们不取他啊, 可以忽略不计啊,这只忽略不计,那么这种我们称为三四个马原则啊,这就是三四个马原则啊,这是我们的正态分布的知识点,我们看后面的练习 啊,第一题呢就是,哎,这是标准正态分布,那么 x 的密度,我们把这个 miu 呢? miu 等于零, c 个码等于一,带到那个我们的这个 fx, 这叫正太。呃,密度这个函数啊,我们来把这个写一下, 这里面 m 是等于零的,你把零带进去,然后 c 个码是等于一的带进去,哎,我们就可以导出来, 还是他就是等于根号,根号二派啊,这个这个函数呢,就是 fx, 那么就等于根号二派分之一,然后 e 的负二分之 x 平方 啊,这个概率呢?这个概率 x 小于等于零,我先把他的图像画一下呗,他的 对称轴是 x 等于零,然后他就是像一个负十三一样的三包啊。 x 小于等于零的概率呢?当然是对称的一半零点五,那这个呢?小于等于一,那么小于等于一,这是负一,这是一 啊,这是一,那么小于等于一,就是在这个区间上呗。啊,在这个区间上,他绝对值小于等于一,在这个区间 这个区间,那我们这个一呢?是就是 m 是零,那么 c 个码是一,这是 m, 加上 c 个码就是一 c 个码的区间,那么这是固定的零点六八二七,这是固定的概率啊,那么小于一呢? x 小于一,那把这个一左边的所有的都包括进去了啊,包括进去了,那我们可以怎么可以?这是零点五,这全部是零点五,这个对称轴左边的全部是零点五,再加上这一块,这一块怎么算呢?那么就是 刚才计算的零点六八二七除以二呗,那么所以说我们这个是零点五加上零点六八二七除以二就得出来了,最后得出来他的概率呢,是等于零点八 四幺四的啊,那么这个大于一呢?大于一是这部分啊,大于一这这部分的概率,那我就用一减去他行了吗?因为他加他是等于一的,那么得出来是零点一五八六是第一题,我们看第二题 啊,第二题啊,这个随机变量他是等于他的啊,零,呃,这是 miu 是等于零,那个 c 个码是等于二的,这个 miu 等于零, c 个码等于三的,我们要画出他的密度曲线草图,那画一下吧, 那他俩啊,这俩均值是一样,方差,一个 x, 这个方差这个方差小,这个方差大那,那那一个是瘦高的,一个是矮胖的啊,相对 来说他是一个是一个是瘦高啊,一个是矮胖啊,那我就画,再画一个瘦高的 啊,再画一个瘦高的 啊,再画一个瘦高的,那么上面这个就是 x 啊,这上面上面这个下面这个图形呢?是 y 啊,下面这个图形是 y 啊,越小的话越瘦高啊,越小的是瘦高。那么我们这个焦点是我们可以计算出来的啊,计算通过,通过计算器计算出来,大概是二点多,二点多,那我们这个二呢,大概就在这 在里面啊,这二在这,那我们是现在要求的是谁呢?求的是这个 x 小于等于负二和 x 小于等于二,小于等于负二啊,负二是这这边小于等于负二和小于等于二,那么根据对称性啊,我们根据对称性,那么这这边和这边是相等的,那么所以说他俩加起来是等于一的, 那我们这个概率呢?也就是 x 小于等于负二,他的概率加上他是等于一的,那我们就可以等于他就等于一,减去个 p, x 小于等于二,这是他们的关关系啊。我们看这个 p x 的绝对值小于等于一和 p y 的绝对值小于等于一,这两个的区间。这两个的概率啊,这这两个概率是谁大谁小呢?那这个 我们画一下,这是一啊,我们这是负一啊,这是负一,那么这个呢?是一啊,一个是负一,一个是一,那对于 谁的概率大?那谁的面积大,谁的概率大?那显然是上面这个啊, x 这面积比他下面下这外的面积就是这部分啊,这部分面积 x 面积呢?还包括这一部分面积,那么所以说他大于他啊,这是很明显的。 我们看第三题。
542洪邦数学







