从哪里看开了k模型
粉丝1.1万获赞5.0万
相关视频
 00:47
00:47 00:46
00:46 01:39查看AI文稿AI文稿
01:39查看AI文稿AI文稿大家好,这期视频教大家怎么设置 k 模型,新版本英伟达是不支持 k 模型的,先打开文档中 c 盘文件路径安装一下, 然后把这个文件复制到桌面上,打开方式以记事本在里面输入镜子,英伟达自动更新代码,从代码指示器把英伟达镜子更新代码复制 复制进去,然后保存到桌面,把修改好的文件复制到文件夹中,并且替换掉, 然后打开画质工具包输出,这边已经安装好老版本英伟达,安装好后直接打开英伟达 app, 找到三角洲,打开 diss 模型预设,把模型预设改成 k 模型并且应用,然后打开画质工具包, 找到复制这个文件,并且以管理员运行,找到粘贴还是以管理员运行,打开 diss 四器,打开 wegame, 找到三角洲,并且启动这边输出,直接快进到游戏加载面, 大家可以看左下角的字母四 k 就 成功了。课后小节必须驱动版本要到达五百七十以上才可以,这期视频就到这里,觉得视频对你有帮助可以点个关注,下期再见。
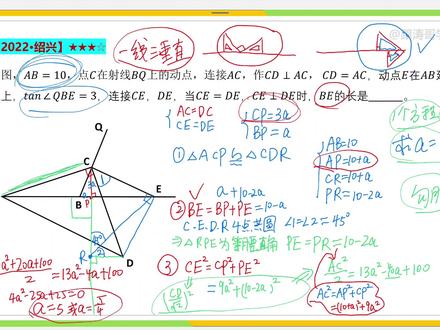 13:28查看AI文稿AI文稿
13:28查看AI文稿AI文稿中考数学有一个几何模型,江湖人称 k 字模型叶叫一线三垂直,你以为他很简单,当他换个马甲你就找不到了?看题 有一定的难度啊,因为他的条件比较隐含,而且这道题他其实考察了一个几何模型,这个几何模型呢,我们很多同学都见过,叫一线 三垂直,但是这个一线三垂直和我们通常的是有很大的区别的,我们通常见的一线三垂直是怎样的呢?我画一个图, 是一条直线,然后呢,在直线上有一个直角,好,然后做两个垂线,左边红色和右边红色三角形就是相似的,或者是全等的,是这样的一线三垂直。但是这道题中他的一线三垂直是有别于刚才所讲的这样的,因为一线 三垂直。还有一种情况,大家看着啊,我画一条直线,好在这个直线上呢,有这样一个直角,同时呢,再做一个直角,再做一个直角,大家看一下, 一个直角,两个直角,三个直角,这也是一线三垂直。于是呢,上面这个蓝色的三角形和下面这个蓝色三角形也是相似,或者是全等的。而这道题他所考察的就是这第二种一线三垂直, 而且它非常的隐蔽。好了,那我们来看题,首先给出一个等腰直角三角形, a, c, d 啊,大家看,这个是一个等腰直角三角形,那也就是说 a c 是等于 d c 的,然后呢,这里有一个九十度,同时这个角 q b, e, 蓝色这个 角他的正切是等于三,哎,这是不是非常特殊的一个条件,一定要用上。那么第二个等腰直角三角形,大家看把异地给连起来, 这个蓝色的三角形也是等腰直角三角形,那么一角呢?是直角,那我也写上 c e 等于 b e, 对吧?有两对相等的线段。好,现在要求什么呢?求 b e 的长, 这条蓝色的 b e 等于多少?哎,这个题目看起来其实很简单啊,就是两个等腰直角三角形,一个两个同时呢, 有一个正切为三的角,现在要求比一的长,对吧?这个条件看起来并不复杂啊,那该怎么办呢?我们的突破口当然是这个正切值给呢 你一个角的正切,那我们是不是就可以马上构造一个直角三角形,把这个正切直给利用起来啊?所以我们很容易想到的是过 c 点 做一个垂线,哎,这个垂足呢?我们记住 p 点可以吧,就这个垂足呢?那么于是根据这个蓝色的角正切是三的话,我们是不是可以设未知数啊?我们可以设 c p 等于三倍的 a, 那么 b p 是不是就等于一倍的 a 啊?因为是三比一的关系嘛,三 a b p 呢?就是 a。 好, 这个时候我们是不是就把这个角给利用起来了?但是这样做出来的话有什么用呢?他和他对于我们求 b e 这条线段有什么帮助吗?暂时看不出来,但是这个时候大家有没有发现有 一线三垂直的可能?那啦,大家看一下啊,角 c 是不是一个直角?好,我们刚才做了这条垂线 c p, 如果把它延长的话,大家看往下延长。好,那么 因为这里是一个大的直角,绿色的画出来,这个没问题啊,这里角色又是一个直角,两个直角了,那么过低一点,再做一个垂线,哎,这是不是第三个直角,这个时候是不是就构成了一线三垂直的模型啊? 哎,就是我们上面这种情况呢,你看,其实就是把上面这个我们第二种一线三垂直的情况把它给倒过来嘛,就是一条直线,然后呢有一个直角,然后第二个直角, 第三个直角,那么左边三角形和右边三角形就是相似的,或者是全等的啦。好,那么我们构造出了这样的一个一线三垂直的模型之 之后啊,你看啊,这个绿色的三角形和这个绿色的三角形是相似或者是全等的,那我们先写上,至少是相似的。所以第一步三角形 a、 c p 是相似于三角形 c、 d, 那这个垂足呢?我们记住 r 点,哎, r 好,也就左右两个三角形相似,那么我们又能够根据 a c 等于 cd 是不是相似三角形的对应边相等,那不就是两个三角形全等吧?哎,根据 ac 等于 cd 的话,你看 ac 等于 cd 对应边相等,那这两个三角形就全等了,这样就比相似更加特殊。 好,这两个三角形全等,这就是我们的第一步做好了,接着我们就能够把图中的一些线段分别用 a 这个参数来表示的,因为还有一个已知的值, a b 等于十,大家看 a b 等于十,根据 a b 等于十, a p 呢?大家看, a p 的长是不是就是十加 a 呀?对吧? 十加 a 同时 c r 的长,这条蓝色的线段 c r 的长是不是也是十加 a 啊?因为三角形全等嘛, a p 和 c r 是对应边以及呢 p r 的长, 这一节,大家看这一段是不是就是十加 a 减去三 a 啊,那就是十减二 a, 好,这些呢,就是我们已知的线段,这就是我们啊,根据三角形全等和正切值设出来了 a 和三 a 得到 的一些隐含条件,接着我们继续往后做,我们的目标是干什么?求 b e 的长,对吧?你看 b e 的长在这里, b e 的长 第二步啦,我们目标求 be 的长,他实际上等于 bp 加上 pe, 对不对?这个 bp 他就是我们刚才所设的这个 a, 那么关键就是把 pe 给求出来,然后把 a 给求出来, be 是不是就可求了?好,那么我们再把目标放到 pe 上来。哎, p e 这条线段它非常的特殊,为什么呢?我们首先能够得到四点共圆,大家看啊, c 点、 e 点、 d 点和 r 点是四点共圆的, 为什么四点共圆?因为角 e 和角 r 是不是对角互补啊?所以呢,首先 c 点、 e 点、 d 点和 r 点四点共圆,四点共圆之后呢,我们根据共边角相等,大家看啊, 这个角叫角一的话,这个角叫角二的话,很容易得到角一等于角二,这个没问题吧?而角一是什么?我们刚才讲了,这个蓝色的三角形是一个等腰直角三角形,已知条件吧,角一等于四十五度,所以角二呢,也是四十五度,既然角二是四十五度的话,那上面这个角 是不是也是四十五度啊?好,于是大家看一下,这个绿色的三角形是不是一个等腰直角三角形啊?所以就能推出三角形 r, p e 为 等腰直角三角形。哎,得到等腰直角三角形之后呢, p e 就等于 p r, 而 p r 上面是不是有啊?在这里,哎,直接写下来了嘛,就等于一十减二 a。 好, 我们已经写到这里之后,接下来就一切迎刃而解了,就是做计算呢?为什么呢?我们刚才讲了,求 b e 的长,他实际上等于 b p 加 p e, b p 是等于 a, 而 p e 等于多少? p e 是等于十减二 a, 对吧?那也就是说十减二 a, 那最后相加嘛,就是十减 a。 好,那么我们只需要求出 a 等于多少, 那一切这个 b 的长是不是就求出来了?因为 b 的长是十减 a 嘛,那如何求 a 呢?这个 a 是不是一个未知数啊?而且只有一个未知数,我们只需要干 什么构造一个方程就可以了,也就是寻找一个等量关系吗?那么在这个图中有很多直角三角形,那勾股定理是不是就是一个天然的构造等量关系的重要的工具啊? 勾股定理,哎,这个思想啊,大家一定要重视啊,勾股定理能够构造一个天然的等量关系,所以呢,就能够求这个未知数,具有一定的可能了。那么我们就找这样的一个直角三角形,大家看啊,直角三角形 c p e, 这个红色的,大家看这个红色的直角三角形 c p e。 第三步,我们很容易得到 c e 的平方,等于 c p 的平方,加上 p e 的平方。哎,我们只需要把 c e, c p 和 p e 都用 a 来表示,然后把这个方程 解出来,那 a 是不是就求出来了?好,那我们一个一个来啊,我把等号先写在这里,我们先看等号右边的 c p 等于多少 cp, 他是不就是三倍的 a 呀?哎,在这里呢,已知条件都有,所以呢,就是他的平方就是九倍 a 的平方,加上 pe, pe 的长,是不是就是这里有啊?十减二 a, 对不对啊?哎,加上十减二 a 个平方好,那么左边 c e 我们能够用 a 来表示就可以了吧? c e 在哪里啊?我把这个擦掉啊。 c e 在这里, c e 我们好像跟 a 是没有关系的吧,但是大家发现了吗?我们又一次利用这一个等腰直角三角形 c e, 它是不是等于 c d 去除以根号啊? 二啊,对吧?因为是等腰直角三角形啊,而 c、 d 的长呢,我们是可以表示的。为什么呢?我们先一步步来看啊, c e 是等于 c d 除以根号,所以它的平方呢,要加上来。好,我们把这个等式先写过来,就是 c d 的平方除以二,等于 得三倍 a 的平方减四十倍的 a 加上一百,是吧?我做了一个化减啊。好,我们关注 c d 的平方就可以了。 c d 的平方,你看 c d, 它是不是等于 a c 呀?这个没问题吧,所以 c、 d 的平方就可以把它写成 a c 的平方。好,那 a c 的平方是不是又有一个直角三角形?大家看蓝色的这个直角三角形,再画一遍啊,蓝色的这个直角三角形,所以 a c 的平方,我写上来。 a c 的平方,它是不是就是等于 a p 的平方加上 c p 的平方啊?因为蓝色的直角三角形呢? a p 在这里, c p 还是三 a, 对吧?所以 a c 的平方就等于 a p 的平方。十加 a 的平方, 再加上 c p 的平方。三 a 的平方就九倍 a 的平方好,那么 ac 的平方我们知道了,把它带到上面来,那么这是不是又得到一个关于 a 的方程了?好,那么最后化减了,都写到最左边了啊, a, c 的平方展开得到十倍, a 的平方加上二十倍的 a, 加上一百除以二。好,要等于右边的一十三倍, a 平方减四倍, a 加上一百,对吧?就解这个方程,把 a 解出来,然后就能够迎刃而解了吧,因为 b, e 的长是十 减 a, 好,我们解这个方程,做一个化减吧,啊,这个是四十倍的 a 啊,那么最后呢,我们把这个方程做一个化减,可以化减为四倍, a 的平方减二十五倍的 a 加上二十五等于零,这个是一个简单的计算,不再追数了,最后解得 a 等于五或者 a 等于四分之五。好,你把 a 这两个答案当然都可以带进去,所以呢,用一十啊,减去 a, 最后 b 的长呢,就是五或者四分之三十五。 好了,那么这道题呢,就算是做完了啊,有一定的难度。这道题啊,他的突破口在哪里呢?他的突破口在于把这个正切为三的角构造到一个直角三角形中 去,大家看啊,就是中间这个 c, b, p 这个绿色的直角三角形,把它做出来之后呢,然后我们能够发现这一条线啊,这一条线刚好是有一个直角的,然后就把它延长之后,构造出了一线三垂直的模型啊,这个一线三垂直特别的特殊,然后呢, 多次的利用勾股定理,我们用了几次勾股定理啊,两次勾股定理吧,第一次勾股定理是在这个红色的三角形中,第二次的勾股定理呢,是在左边这个红色的三角形中,而且中间有一些条件转换,有一定的复杂性,大家好好要体会一下。而且啊,这个图中 已知条件是有两个等腰直角三角形的,第一个这个红色的,第二个这个红色的,但实际上我们根据四点共圆的模型发现了 这里还有第三个等腰直角三角形。所以这道题中等腰直角三角形呢?一共有三个,哎,这道题呢,有一定的难度啊,大家好好体会一下。
541跟涛哥学数学 02:20查看AI文稿AI文稿
02:20查看AI文稿AI文稿哈喽大家好,我是艳阳魔性的角克,今天为大家分享来自 a k a 家的新系列 k 系列的第一个产品 k e l a k 幺二。老规矩还是先从外部开始, 后面我们再打开看内部细节。整段前结除了护目,其他部位为六系铝合金 cnc 工艺还原造型的火帽有弹簧消钉固定。往后看就是六系铝合金做成的前机瞄和导气部分。导气阀门同样也做了弹簧消钉的还原设计, 按注销钉可以旋转拆卸,下方也有背带的圆形卡环,装饰性的导气分两段螺纹固定。那么大家关心的电池仓其实还是在护目里面的,安装电池需要拆掉护目内部的那段导气管。电池仓的大小和现在的 a 系列 基本一致,电池接口为 xt 三零 ak 幺二造型的尼龙护目上下都具备二十毫米的标准刀轨,左右两侧也有小刀轨。 打开护目,凹凸设计的 cnc 一体成型套管,内管和套管也是一体的,套管座两侧也有模拟的焊纹装饰。机侠主体部分为尼龙材质,左侧也有六 n 七零等还原刻字 cnc 的铆钉,视觉效果还是挺不错的。 右侧是钢制的战术拨片保险二连发,最下面为单发档位,上部为尼龙上盖,搭配六缕 cnc 挡滚条,后部为同样材质工艺的可调后罩门,尾部还有还原的钢片包裹。 拆下套管座处的护目卡销可以向后打开后盖。回弹部分由拉线结构搭配六铝 cec 机片,拉线结构可以支持全形成回弹。继续往下看, 弹夹释放为钢制的护工握把式尼龙一体住宿握把的手感非常不错,两侧也有还原的金属小零件,握把底部是电机的调节螺丝,后面的小孔顶住后就可以打开电机握把了。 ak 幺二的弹夹也是重新设计的,弹簧触电式的供电结构有效改善了供电接触问题。 大家关心的可视窗也做出来了,底部为还原的金属钢片,而且这款弹夹是可以通用 a 系列其他产品的,晃动问题其实也有减小。尾部为 a k 幺二造型的尼龙厚凸六档伸缩调节固定接口释放结构也是与智能。
847烨阳模型














