蒙特卡洛生成随机数必须是正态分布么
各位同学大家好,那么今天我们来说一下项目管理当中的蒙特卡洛分析法。蒙特卡洛分析法呢,在项目管理当中,它属于定量风险分析,它是一种采用随机抽样统计来估算结果的一种计算方法。 那么在项目管理当中,蒙的卡罗分析方法的执行步骤呢?是按照下面的步骤来执行。 第一个呢,首先我们对每项活动啊来输入他的最小最大和最可能的一个估计数据, 并且为其选择一种合适的经验分布模型。第二步呢,计算机会根据我们上面的输入,利用给定的某种规则,快速实施充分大量的一种随机抽样。那么第三步就是对随机抽样的数据来进行必要的数学计算来求出相关的结果。那第四 四步呢,我们对求出的结果来做统计学的处理,来求出最小值,最大值以及数学期望值和单位的标准偏差。那第五步呢,我们要根据求出的统计学处理数据,让计算机自动生成概率分布曲线和累积概率曲线, 那么通常呢,是基于正态分布的概率累积的 s 型曲线。那第六步呢,就是我们要根据累积概率曲线来进行项目的风险分析。那么以上呢,就是在项目管理当中蒙德卡的分析法,它执行的步骤。
粉丝1718获赞6195
相关视频
 14:13查看AI文稿AI文稿
14:13查看AI文稿AI文稿欢迎观看二零二二年树之道系列的第一期节目,这里祝所有的小伙伴新年快乐,新的一年里身体健康,事业、学业、家业顺利。 在之前五期节目中,我们分别用三期节目介绍了马尔克夫练的基础知识,两期节目介绍了蒙特卡洛模拟的两种抽样方法。 今天我会把这两个主题结合起来,带大家走进马尔克夫列蒙特卡罗方法 mark of chain monte carlo method 以下简称为 mc mc, 错过前面节目的朋友们完全不用担心,我会在本期节目中将重点概念再为大家重温一遍, 相信节目之后你一定能够更好的理解 mcmc 这以数据分析数据科学领域中的核心知识点。 由于本期内容涵盖知识点非常多,所以我会分四个章节进行介绍。一、从上两期节目中所介绍的逆转换接受拒绝抽样方法的局限性出发,引出为什么我们需要设计新的抽样方法。 二、为什么马尔克夫练元素的加入能够有效提升抽样效率?这背后的理论依据又是什么?三、 mcmc 方法之 metropolis hastings 算法的设计思路详解。 四、使用 r 语言对 metropolis 算法进行模拟演示。那么现在就让我们正式进入本期节目的核心内容。第一章,逆转换接受拒绝抽样的局限性在 前两期节目中,我们分别介绍了使用逆转换方法和接受拒绝方法进行抽样。在使用逆转换方法的过程中, 需要先对目标概率密度函数 pdf 求积分,得到累积分布函数 cdf, 再对 cdf 进行反函数求解,得到从均匀分布到目标分布的转化函数,这样就能实现从简单均匀分布出发,得到满足复杂目标分布的随机值了。 但之前求积分和求返函数的步骤却能给大家造成足够的麻烦,因此我们有了第二种抽样方法,接受拒绝方法。 接受拒绝方法中,我们需要设计一个简单的建议分布函数 gx, 再通过放大系数 m 让 m 乘 gx 落于目标函数 fx 上方,通过在 x 轴上根据 gx 生成随机值坐标 a, 然后在 y 轴上根据零到 m 乘 ga 的均匀分布生成随机坐标 b。 通过判断坐标 ab 是否能够落入接受区域来判定 a 能否最终被成功抽取。 不过该方法也有他的局限性,由于 m 乘 gx 需要处处大于我们的目标函数, 因此当目标函数是如图中形态的话,接受区域占比会非常小,真正实操阶段会耗费大量的时间和资源才能抽取足够的样本。了解了以上抽样方法的 线之后,我们再看 mcmc。 第二张 mcmc 为什么能够有效提升抽样效率呢?之前接受拒绝抽样效率低的原因之一是由于其没有充分利用前期的信息。 比如,当根据建议分布 gx 抽样出的 xn 恰好出现在其目标分布中的高密度区域时,如果下次抽样 xn 加一能够在这附近抽取,其接受的成功率自然也会相应较高。 但在接受拒绝方法中的每次抽样都是独立的,且建议分布函数不变, xn 的信息在下次抽样动作前会完全抹去,所以有相当的概率下次抽样会返回高拒绝区域的值。因此, 从直觉出发,我们需要让这个建议分布动起来,保留前期有用信息,并影响下次抽样。这样抽样效率是不是就更优了呢?为此,我们将马克夫恋的思想加入其中,最终流程会是这个样子的。 假设,我们根据初始的建议,正态分布 g x 零 c 个码进行抽样, x 零为初始设置的均值, c 个码为标准差得到 x 撇。假如 x 撇符合我们预设的规则, 我们则把 x 撇赋予 x e 作为鸡的均值参数用于下一次抽样。相反,假如 x 撇不满足规则,那么我们就会将原 零的值负于 x 一作为鸡的均值参数用于下一次抽样。这个链条会一直持续下去并收敛,达到稳态。 在马尔克夫练的节目中,我们介绍了稳态分布转移矩阵的概念。假如马尔克夫练的转移矩阵满足便利性,那么它存在唯一的稳态分布。现在你可以这样理解上面的 mcmc 链条, 我们就是需要设计这样一个判断规则,他能够起到转移矩阵的作用,让该链条能够收敛至稳态分布。而这个稳态分布就是我们目标函数概率密度分布了。 达到稳态后抽取的随机值就等同于从目标分布中进行抽样了。 到这里或许你还会有些迷茫,没关系,可以重温我们数字到十八到二十二级,然后再来体会我上面说的内容,一定会豁然开朗。 接下来让我们深入 mcmc 的具体算法之 match prolex hastings 算法。我会将上面的理论思路具象化,通过 mh 算法帮助大家更好的理解其精华。 第三张, metropolis hastings 算法 mh 算法的设计用到了马克夫链中一个叫做细致平稳 detailed balance 的概念。 我们假设有这样一个满足便利性的马尔克夫链,各状态已达到唯一的稳态分布 s, 如果其转移矩阵 t 满足下面的公式 s i i 乘以 t, i to j 等于 s, j 乘以 t, j to i, 我们撑起满足细致平稳条件。我会借用十九集中的例子介绍这里需要特别注意的两个点,第一点,并不是所有的稳态分布都满足细致平稳条件,比如该例中的稳态分布不满足细致平稳。 第二点,满足细致平稳条件的状态分布达到稳态分布。稳态分布有如下特点,项链 s 乘以矩阵 t 等于项链 s, 他的矩阵表达形式如下, 为了论证细致平稳条件也是稳态,我们就需要验证上述等式在细致平稳下也成立。 我们对细致平稳条件等式两边根据哀求和,然后等式右边做如下调整得到,因为从 j 状态转移去至所有状态的概率和为一。 因此最终下面的等式成立,符合稳态条件,证明完毕。我们可以用下面通俗的语言来进一步解释细致平稳公式。 从等式的两边来看,他等同于在说从处于状态 i 下期转移到状态 j 的概率与从处于状态 j 下期转移到状态 i 的概率相同, 他将对后面 mh 算法的构建起到决定性的作用。还记得第二章中的这句话吗? 需要设计这样一个判断规则,他能够起到转移矩阵的作用,让该链条能够收敛至稳态分布,而这个稳态分布就是我们的目标函数分布。那么我们就是需要设计这个规则,能够使上述等式成立。 其实,等式的每一边都包括了两个步骤,步骤一,从旧状态下选出新状态作为候选对象。步骤二,判断是否需要转移至新状态。 我们用具体的数学语言来对这两个步骤进行推倒。步骤一,当已达到稳态,处于状态 i 的概率为 s i, 然后根据建议正态分布 g i c 个码,生成新的随机 值 j。 我们用 g j 基于 i 代表着均值参数为 i 时, j 被抽取出的概率 s i 乘以 g j, g i 则代表了从处于状态 a 下,根据 g i c m 选出了下期后选状态 j 的概率。 步骤二,我们定义 a j 基于 a, 它代表了接受 j 作为 a 转移后状态的概率。 两步相乘得到 s i 乘以 g j, g i, 再乘以 a j g i, 这就完美表达了从处于状态 a 转移到状态 j 的概率。同样的, sj 乘以 gig 与 j 乘以 aig 与 j 则代表了从处于状态 j 转移到状态 i 的概率。 两个公式在细致平稳条件下相等则有,其中 g j 基于 i 乘以 a, j 基于 i 和 g i 基于 j 乘以 a i 基于 j 对应了我们转移矩阵中的 t i to j 和 t j to i。 我们将上面的等式变换一下,得到 metropolis hasting 算法提出了一个满足上市等式的结法如下, 值得注意的是,由于基服从正态分布,它是对称的,那么基埃基于 j 与 g j g i 相等,两者相处抵消上述公式进一步得到精简。现在最后的问题是怎么求 s? 由于我们知道函数 sx 就等同于我们的目标概率密度分布函数 pdfx, 而 pdfx 又等于我们的目标函数 fx 除以标准化常数 c, c 为 f, x 与 x 轴为成的积分值。很多时候 c 很难求解, 那么我们把 s j 等于 f j 除 c 和 s i 等于 f, i 除 c 带入上述等式,得到最终公式 a j 基于 i 等于一和 f j 除以 f i 中的最小值。这便是最初的 major produce 算法。而后期加入的 g i, g 与 j 除以 g, j 基于 i 作为 hastings 参数,则进一步扩大了该算法在非对称建议分布下使用的适用性。 到这里,之前提到的规则就已经设计出来了,我们有了建议分布 g, 同时有转移接受规则 a, 那么就可以顺着这个规则链条达到稳态分布,完美实现从目标分布中抽取随机值了。 让我们进入最中章第四章 metropolis 算法 r 语言实力在这个例子中,我们有一个,有两个正态分布,根据相应权重构成的新分布,设计一个 标准差位零点五变量 x 作为均值的正太分布。抽样公式 q, 为后续从该分布中抽取随机数做准备,需要提点标准差,可以尝试不同值来比较最终的抽样效果。 设置一个包含了一万个值的数据集合 x 覆盖初始变量 x 一为一 初始值,可以尝试不同值来比较最终的抽氧效果。接下来进入循环语句,循环九千九百九十九次, 每次循环哎。将当前的 xi 值作为变量 x 录入建议正太分布抽样公式 q 中得到心值 x j。 将 x i, x j 套入第三张 当中的 metropolis 公式,计算接受概率 a。 为了做出是否接受 xj 的决定,我们可以引入一个服从零到一间均匀分布的随机值,让他与 a 比较。 当 a 大的话,用 x j 值覆盖 x i 加一,否则用当前 x i 值覆盖 x i 加一。 完成循环后,我们可以绘制更新后的数据集合 x 的直方图,可以看到其能够很好的满足目标函数分布。 新年第一期数字到节目就到这里了,希望大家喜欢本期节目。今年除了本系列之外,我还会开一档新的节目,和大家分享一些工作学习方面的心得,让我们在新的一年里共同进步,那么下期节目再见!
575funincode 26:22
26:22 05:50查看AI文稿AI文稿
05:50查看AI文稿AI文稿蒙特卡罗算法,我虽然这么说,但是更准确的来讲,蒙特卡罗不是某一个算法,他更是一种方法,那么这种方法呢,是一种统计学的方法,是一种模拟的方法, 所以很多时候蒙特卡罗算法也可以称作为蒙特卡罗模拟。那么蒙特卡罗模拟是二战期间,为了解决这个原子弹中的一个问题,裂变物质的中子随机扩散问题,美国的数学家冯诺伊曼和乌拉姆等提出的一种统计方法。 那么由于是在战时,所以呢,他们没有为这种统计方法起一个看起来非常容易理解的名字,比如说这种方法不叫随机模拟方法,这样的话呢,如果敌方监听了他们的对话,可能就能猜出他们的研究手段,为此呢,他们起着 一个代号,这个代号呢叫蒙特卡罗。具体为什么使用蒙特卡罗这个代号呢?这是因为蒙特卡罗他是当时世界上最著名的一个赌城,在摩纳哥, 而我们这种随机模拟的手段和赌博的关系非常的大。那么在我们这一章的最后两小节,其实讲的都是将摩托卡罗方法用在类似于赌博的这种能不能中奖的游戏中,来计算玩家的盈率, 所以以这个城市的名字作为这个方法代号。当然了,现在这个世界上最著名的赌城应该叫做拉斯维加斯了, 也正因为如此呢,其实也有一个拉斯维加斯算法,那么有兴趣的同学呢,可以查一查资料,看看拉斯维加斯算法是什么意思。那么以后有机会的话,或许我还可以向同 同学们分享更多相关的问题,其实是非常有意思的,那么具体什么是蒙特卡罗方法呢?其实非常的简单,就是通过大量的随机样本来了解一个系统,进而得到索要计算的值,那么这里头的关键字就是大量随机。 我们在这一张的后续就要举三个使用蒙特卡罗方法的例子。在这一小节,我们尝试使用蒙特卡罗的方法来计算派制,这是蒙特卡罗方法的一个经典的应用, 所有了解蒙特卡罗方法的同学都应该知道这个应用,但是这个应用可能对于有些同学来说会觉得比较枯燥,那么在这一张的最后两小节,我会使用蒙特卡罗方法来求解两个类似于赌博问题的一个盈率的问题。 那么在这里大家要注意,蒙特卡罗方法使用大量的随机样本来去获得我们所要计算的这个值,但是获得的这个值不一定是真值, 而是一个近似纸。那么事实上蒙特嘎啦方法就是利用这样的一个原理,在一些问题中,我们可以使用大量的随机样本去模拟,我们的样本量越大,最终模拟出来的值就相应的会越准确。 那么在这一小节,我们首先来看用蒙特卡罗方法如何求派的值。大家知道我们可以用派的值去求圆的面积,或者是圆的周长,但是可能很少有同学们去追溯派这个值到底是怎么来的。那么对这个问题感兴趣的同学呢,可以查阅一下资料, 是一段非常有意思的数学历史。不过在这里我们探究一个问题,假设我们现在并不知道派的纸的话,希望你获得一个派的近似纸的话,那应该怎么做呢? 在这种时候我们就可以使用蒙特卡罗的方法,大家可以看在这个图中其实是一个正方形,在这个正方形中有一个直径和这个正方形的边长一样的圆。那么首先我们来看在这个图形中圆和这个正方形之间的关系, 我们知道圆的面积是等于派啊方,而我们的正方形的面积在这里,它的边长是二乘以啊,所以就是二啊,乘以二啊,最后等于四啊方。那么通过这两个式子,同学们就看出来了,我们圆的面积除以方的面积,这两个啊方就可以约去就应 该等于四分之派,进而派这个值就可以表达成四倍的圆的面积除以方的面积,所以我们想办法获得圆的面积和方的面积就可以了。那么现在剩下的问题就是,圆的面积我们怎么获得呢? 在这里就使用蒙特卡罗的方法来近似的模拟圆的面积,我们可以向这个正方形中随机的打入一个点, 那么这个点可能会落入园内,也可能会落入园外,那么在我这个图片里呢,落入园内的点我就用红色表示,落入园外的点我用绿色表示,这样的点大家可以想象,如果 打的非常多的话,红色点的数量就可以近似的来表示圆的面积,而红色点加绿色点的 数量就可以近似的来表示方的面积,当然这个面积的值会很不准确,但是红色点的数量去除以红色点加上绿色点的数量,也就是我们总点数的数量,这个笔值应该是接近于 圆的面积和方的面积的比值的,而且我们打的点数越多,这个值应该相应的就越接近,因此我们的派这个值就可以等于是四乘以我们打进来的红色点的数量除以总点数。 那么我们使用这样的方式,就利用随机模拟的方法来求出了派的值怎么样,是不是觉得很神奇?那么下面我们就来具体的实现一下,看看这样模拟的结果是怎样。
683长歌+ 05:04查看AI文稿AI文稿
05:04查看AI文稿AI文稿能通过随机数来计算圆周率吗?这是一个正方形以及它的内接圆,随机的往这个正方形上打点,总打点数记作 t, 落在圆中的点数记左 n, 用 n 除以 t 再乘以四来求派。 我们来看看随着 t 的不断增大求到的 pad 近似值情况。随着输入的点数越来越多,误差率变得越来越小, 求出来的圆周率近似值越来越接近真实的派。这是一个非常经典的通过几何概率来求派的方法,而这种通过随机数来获得近似结果的方法被统称为蒙特卡洛方法。 二十世纪四十年代,冯诺伊曼斯坦尼斯拉夫乌拉姆和尼古拉斯梅特罗波利斯在洛斯阿拉莫斯 国家实验室为核武器计划工作时发明了蒙特卡洛方法,因为乌拉姆的叔叔经常在摩纳哥的蒙特卡洛赌场输前得名。 蒙特卡洛方法是对数学运算的近似估计。当一个问题无法直接通过数学推导来进行求解时,当计算机无法在指定时间内完成推导时,就需要考虑是否可以通过蒙特卡洛法来解决这个问题了。 实际工程中,一个误差足够小的近似估计是可以被接受的,因此蒙特卡洛方法有着广泛的工业应用。 再来看一下用蒙特卡洛方法求定积分。如果一个非常复杂的函数 f x, 很难用数学逻辑推倒的办法来求函数的定积分,有办法解决吗?划定函数的一段区域,并在 在这段区域中画出一个矩形,然后随机的往这个矩形区域中打点。当点数足够时,就可以通过统计函数下方的点数与总点数的比值来计算积分了。 你不能说这是一个笨办法。对于许多不规则局限来说,用蒙特卡洛方法可能是唯一的选择。 在人工智能领域,最被人们称道的蒙特卡洛方法是蒙特卡洛术搜索。在人工智能中,人们用博弈术来表示一个游戏 不艺术的每个节点都代表一个状态,其下一个状态的结合构成了状态的子节点。比如任意一个棋盘局面就是一个状态,该局面下所有可能落子的情况形成的新局面集合构成了该状态的子节点。如果是比较 简单的游戏,完全可以穷举所有的状态,然后根据穷举的结果得到最优解。事实上却无法这么做。拿围棋来说,状态数比可观测宇宙中的原子数还要多。没有计算机可以做这样的穷举。 根据大数定理,当采样数量足够大的话,采样样本可以无限近似的表示原分布。蒙特卡多数搜索就是这样一种用随机采样来作为近似估计的方法。他通过大量自博弈来寻找最有可能走的节点。 自博弈是指让计算机模拟两个选手从当前棋盘局面开始,用随机或简单策略开始不易的方法。蒙特卡路数搜索需要定义一个策略来选择当前局面下最有可能走的子节点,展开这个子节点,然后基于这个节 点完成一次自博弈,最后记录自博弈结果并更新相关数据,重复这个过程,直到满足停止条件。那这个选择策略该如何定义呢?可以指开胜率吗? 不行,因为很可能节点尽管不好,但随机走死的时候赢了一盘。博弈的次数小的时候,胜率并不致信。为了解决这个问题,人们定义了一个叫 uct 的公式。 pui 是 i 节点营的次数, ni 是 i 节点的访问次数, c 是常数,用来调节博弈的次数所占的权重,而 t 则是总访问次数。 公式中加号前的部分是胜率,后面部分的曲线是这样的,随着访问次数的增加值越来越小。因此 u、 c、 t 更 更倾向于选择那些还没怎么被统计过的节点,避免了胜率高、制信度低的问题。不停的重复这个自博弈的过程,每次都选择 uct 值最高的那个节点进行自博弈,重复多次之后,访问次数最高的那个节点就是最佳节点。 这就是蒙特卡洛数搜索的全部过程。我们可以根据需要设置蒙特卡洛数搜索的停止条件,比如十秒之后,再比如一百万次自博弈之后。 自博弈次数越多,算法的表现就会越发优秀。当然,如果自博弈次数能接近于无穷大,那么我们也能得到最优解。今天的讲解就到这里,您可以关注梯度世界,了解更多精彩内容。
1200梯度世界 05:07查看AI文稿AI文稿
05:07查看AI文稿AI文稿能通过随机数来计算圆周率吗?这是一个正方形以及他的内接圆,随机的往这个正方形上打点,总打点数记作 t, 落在圆中的点数记作 n, 用 n 除以 t 再乘以四来求派。我们来看看随着 t 的不断增大,求到的派的近似值情况。 随着输入的点数越来越多,误差率变得越来越小,求出来的圆周率近似值越来越接近真实的派。 这是一个非常经典的通过几何概率来求派的方法,而这种通过随机数来获得近似结果的方法被统称为蒙特卡洛方法。二十世纪四十年代,冯诺伊曼斯坦尼斯拉夫乌拉姆和尼古拉斯梅特罗波利斯在洛斯阿拉莫斯 国家实验室为核武器计划工作时发明了蒙特卡洛方法。一位乌拉姆的叔叔经常在摩纳哥的蒙特卡洛赌场书前得名。 蒙特卡洛方法是对数学运算的近似估计。当一个问题无法直接通过数学推导来进行求解时,当计算机无法在指定时间内完成推导时,就需要考虑是否可以通过蒙特卡洛方法来解决这个问题了。 实际工程中,一个误差足够小的近似估计是可以被接受的,因此蒙特卡洛方法有着广泛的工业应用。 再来看一下用蒙特卡洛方法求定积分。如果一个非常复杂的函数 f x, 很难用数学逻辑推倒的办法来求函数的定积分,有办法解决吗?划定函数的一段区域,并在 在这段区域中画出一个矩形,然后随机的往这个矩形区域中打点。当点数足够时,就可以通过统计函数下方的点数与总点数的比值来计算积分了。 你不能说这是一个笨办法。对于许多不规则局限来说,用蒙特卡洛方法可能是唯一的选择。 在人工智能领域,最被人们称道的蒙特卡洛方法是蒙特卡洛术搜索。在人工智能中,人们用博弈术来表示一个游戏 不艺术的每个节点都代表一个状态,其下一个状态的结合构成了状态的子节点。比如任意一个棋盘局面就是一个状态该局面下所有可能落子的情况形成的新局面,结合构成了该状态的子节点。如果是比较 简单的游戏,完全可以穷举所有的状态,然后根据穷举的结果得到最优解。事实上却无法这么做。拿围棋来说,状态数比可观测宇宙中的原子数还要多,没有计算机可以做这样的穷举。 根据大数定理,当采样数量足够大的话,采样样本可以无限近似的表示原分布。蒙特卡多数搜索就是这样一种用随机采样来作为近似估计的方法。他通过大量自博弈来寻找最有可能走的节点。 自博弈是指让计算机模拟两个选手从当前棋盘局面开始,用随机或简单策略开始博弈的方法。蒙特卡多数搜索需要定义一个策略来选择当前局面下最有可能走的子节点,展开这个子节点,然后基于这个节 点完成一次自博弈,最后记录自博弈结果并更新相关数据,重复这个过程,直到满足停止条件。那这个选择策略该如何定义呢?可以指开胜率吗? 不行,因为很可能节点尽管不好,但随机走子的时候赢了一盘,博弈的次数小的时候胜率并不致信。为了解决这个问题,人们定义了一个叫 uct 的公式, qi 是 i 节点营的次数, ni 是 i 节点的访问次数。 c 是常数,用来调节博弈的次数所占的权重,而 t 则是总访问次数。 公式中,加号前的部分是胜率,后面部分的曲线是这样的,随着访问次数的增加值越来越小。因此, u、 c、 t 更 更倾向于选择那些还没怎么被统计过的节点,避免了高胜率、低至性度的问题。不停地重复这个自博弈的过程,每次都选择 uct 值最高的那个节点进行自博弈, 重复多次之后,访问次数最高的那个节点就是最佳节点。这就是蒙特卡洛数搜索的全部过程。我们可以根据需要设置蒙特卡洛数搜索的停止条件,比如十秒之后,再比如一百万次自博弈之后。 自博弈次数越多,算法的表现就会越发优秀。当然,如果自博弈次数能接近于无穷大,那么我们也能得到最优解。今天的讲解就到这里,如果您觉得我们的讲解对你有帮助,您可以关注梯度世界,了解更多精彩内容。
110返朴 00:36245数学老师
00:36245数学老师 00:59查看AI文稿AI文稿
00:59查看AI文稿AI文稿excel 随机生成数字, 哈喽,大家好,今天咱们讲一个函数,那么这个函数可以随机生成这个指定范围内的数字,那么咱们来操作一下 输入等号啊,在单元格里输入等号,那么输入上面这个函数啊,英文状态下二 andbetwen 那么接下来咱们输入一个括号啊,半个括号,英文状态下,那么咱们输入啊,一百, 一百的意思就是第一个一百啊,逗号,那么是从一百开始,那么至多少呢?咱们至到一千这样,然后补全括号确定, 那么他随机生成的数字就是一百到一千之间的,我们直接啊向下拖动,这样他随机生成的数字。
2120图文设计师东东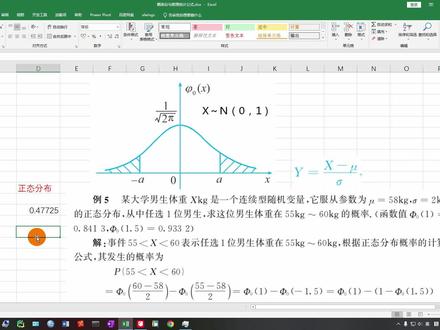 05:00
05:00 04:15查看AI文稿AI文稿
04:15查看AI文稿AI文稿本次课程呢主要是跟大家讲两个随机函数的一个使用,一个是呢,呃,零到一之间的一个随机值的一个函数的使用,另外是一个, 呃整数之间的函数是使用,比如说零到十,十到一百,或者是呢两百到三百之间这样的函数的随机值的生成的一个使用。我们先看零到一之间的这个 啊,符点型的函数的这样一个随机制的生成,那么应用到的函数呢?就是这一个模块,定义这个定义这样一个函数,最后呢 啊定义这样一个模块,然后再返回这样一个字,这样的可以,那么怎么使用?我们把这个函数先把它复制, 放在哪里呢?放在这个我们这一个数据啊,这个面积啊,这个随机啊,随机这个值啊, 它要求呢是一个五点型的或者十万振动型的啊,这个必须是这样的,那么我们先右击他的一个自动计算器,这里面呢我们把这个放进来 粘贴,粘贴这个是呢函数应用是什么呢?应用下面这个代码,这个代码的格式啊,千万要注意啊,格式不对的话也不行,我们把这个先复制过来, 复制再来到这 啊,这样的话肯定运行一下就不行的啊,不行的,这个格式不对,所以我们要把这个格式搞进去,这个地方格式怎么样做?我们把它先删除,再复制一下, 好,这样呢,我们保持这个地方再回车啊,这样一个格式,这个地方也是一样哎,保存这个 在火车这种格式下就可以应用,你看这样就可以了,自动生成了,这个 随机数是零到一的一个随机数,它自动是保持呢,保存了六位,保存六位,那么这个是零到一的随机数的一个生成,随意生成的,那么另外呢一个啊,整数随机数的生成 啊,这个是这个是这个函数,因为这个比较简单一点,用热度函数,热度啊, 我们放到这来就可以了,但是这个呢是整数的,千万不能放在这个地方,这个是是什么呢?是双减角形的或者负的形的,我们放在哪里呢?放在长轴形,短轴形这一些里面,这个呢是长轴形的,我们在用记计算器这样来计算, ok, 那 么下面还有个代码,代码的话呢,是这个 input 来的就可以了 啊,这个呢我们啊括号就打好了,这个地方呢我们是零到十的随机数的生成,我们看一下啊,这个地方呢你看生成了零到十的随机数,那么如果说你把这个地方改成一个一百 啊,一百到五百,这样可不可以呢?也是可以的,你看这就是 啊,一百到五百的水解数的升值,那么这个就啊参数灵活一些,前面那个呢是不能输,不需输入参数的是就是呢零的呢一之间的一个蝴蝶数的函数式的升值,那么今天跟大家就讲到这,谢谢大家。
6地质人










