二次函数与反比例函数的数学画报

ars 函数这样画遇到符号倒过来，整体加三向上移，整体减三向下移 x 加三向左移 x 减三向右移，整体乘三要变瘦，整体除三要变胖。

二次函数全对的方法初中数学二次函数知识点总结定义结论， 二次函数顶点式、 焦点式、待定系数法。求二次函数解析式。 抛物线的翻折轴对称、旋转中心对称需要电子板留一二八。

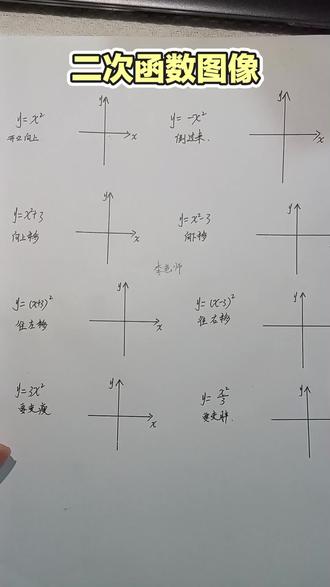
函数图像平移的规律， 这个上加下减长竖项，这个左加右减自变量，这个方法很简单，它一切函数都这样， 这上加下减长竖项，这左加右减自变量，这个方法很简单的，一切函数都这样。

反比例函数，它是咱们初中函数里的关键桥梁，它一边连着一次函数的基础，一边还能为高中的学习铺路。今天呢，我们就从最基本的概念，到图像性质，再到核心应用，一步步带你从零到一，彻底吃透它，新手也能轻松跟上。赶紧集中注意力，咱们马上开始。 现在我们先来讲第一个叫它的定义式，它定义是什么呢？我们把形如 y 等于 x， 分 之 k 这样的函数叫做反比例函数。好，我写出来是这样子啊， y 等于 x， 分 之 k， 把这样的函数叫做反比例函数。 然后我们要知道，在这个里面，它的 k 为常数，并且不为零，也就是说 k 是 一个不为零的常数。还有我们要注意的就是这个 x 和 y， 它均不能为零啊，为啥嘞？首先 x 不 能为零，因为它是分母嘛，由于 k 不 为零，所以 y 也不为零啊，这个一定要知道， x 和 y 都不能等于零。那我们来看这个解析式啊， y 等于 s， 分 之 k， 我 们简单变形就可以得到， x 就 等于 k， 就 等于 x 乘 y 呗，也就是 k 等于 x， y 这个等式就说明了变量 x 和 y 的 成绩，它是一个定值，并且是定值 k。 好， 在说完定义之后，我们就要说它的图像，大家回想一下，我们在之前学过两个函数，一个叫做正比例函数，还有一个叫做一次函数。 正比例和一次函数，它的图像都是一条直线，区别在哪呢？区别就是正比例函数，它的直线是一条过远点的直线，而一次函数它不过远点啊。那么今天我们要学的反比例函数，它的图像是两只双曲线，并且它是怎么样？ 是两条关于远点中心对称的双曲线。这两个双曲线呢？它会无限的靠近坐标轴，也就是无限的靠近 x 轴和 y 轴，但是永远不会和 s 轴、 y 轴相交， 那么它的图像由 k 的 正负来决定。当 k 大 于零的时候，这个图像它位于一三象限， 并且在每个象限内 y 随 s 增大而减小。好，我们先来看一下这个图，我们看在第一象限这一只，你看从左到右， x 是 在增大，但是你看图像是在下降的，也就说 y 在 减小，所以 y 随 s 增大而减小。再看这只，它是同样的从左到右， x 增大，但， 但是图像是往下下降的，所以 y 再减小。所以就是当 k 大 的时候，它的两只，每一只在每个象限内都是 y 随 s 增大而减小。好，那么当 k 小 的时候，它的图像就位于二四象限，在每个象限内 y 随 s 增大而增大。 好，这是第二点它的图像。那么第三个呢？叫做 k 的 几何意义？这个比较重要，考试也考的比较多。有两个结论叫做第一个反比例，图像上任意一点 坐标轴的垂线与坐标轴围成的矩形的面积横为 k 的 绝对值，这是第一个结论。我们先来看第一个结论。好，这我画了个图啊，这是一个双曲线，对吧？好，我们在双曲线上任标一个点 p， 把它的坐标设为 x， 等号 y， 那么任找到一个点之后，我们做这个点到坐标轴的两个垂线。好，我标记为，呃，这个红色画出来了啊。然后垂线与两个坐标轴的交点并标为 a 和 b。 那 这是不就什么构成了一个小的矩形，那么这个矩形的面积是啥呢？就是 k 的 绝对值带来的。我们来推导一下， 我们看这个图，这个矩形什么 a、 o、 b p， 它的面积是等于长乘宽，也就等于什么 p a 乘 p b， 那么 p a 是 啥呀？ p a 不 就是这个点 p 的 纵坐标的绝对值？因为这个图像不一定是位于一三项线，听明白没？所以我们都带上绝对值，保证这个线段它为正啊。所以 p a 就是 y 的 绝对值， p b 就是 这个横坐标的绝对值，就是 s 绝对值。那么 p a 乘 p b 不 就是 x 绝对值乘 y 的 绝对值吗？那么我们就可以把它写成 x 乘 y 的 绝对值。我们刚刚上一节课说过，上一页说过 x 乘 y 的 绝对值，我们刚刚上一的绝对值不就是 k 的 绝对值吗？ 所以这就是第一个结论的推导过程，我们只需要记住结论就行了啊。围成这个矩形面积是谁叫做 k 的 绝对值？那么再看第二个结论叫做，呃，这样做出来的三角形，它的面积 横为二分之一 k 的 绝对值。同理，我们在双曲线上任意一只找任意一点，比如说点 p， 我 们同理设这个 p 的 坐标为 s 轴和 y， 然后向 s 轴做垂线，然后把它跟圆点连起来，这样围成的这个三角形，它的面积等于啥呢？我们知道三角形的面积叫做底乘高除以二 d 就是 o a 高就是 p a， o a 不 就是点 p 的 横坐标的绝对值吗？对吧？这个 p a 不 就是点 p 的 纵坐标的绝对值， y 的 绝对值，底乘高再除以二，所以就是二分之一 s 的 绝对值。乘 y 的 绝对值，也就是二分之一 x， y 的 绝对值，也就是二分之一 k 的 绝对值。这就是这两个二级结论如何证明的？同学们只需要记住就行啊。好，那么这个二级结论如何证明的？同学们来看看。这道题 叫做，呃，看题过。反比例函数 y 等于 x， 这写错了啊， y 等于 x 分 之 k 写错了，应该是 y 等于 x 分 之 k 在 这个反比例函数上，呃， 在它这个图像上，任取一点做 s 轴的垂线，我们大概画个图，啊，画一个草图，好，大概是这样子，在它上任意点，然后向 s 轴做垂线，垂足为 a， 然后 o 是 坐标原点啊 p， 我 们告他，告诉你这个 o a， p 的 面积为四， 让你求 k 的 绝对值。我们知道刚刚说了围成这个三角形的面积公式是啥呀？是不叫做二分之一 k 的 绝对值，它的面积为四，不就是二分之一 k 的 绝对值为四吗？那么 k 的 绝对值等于啥？是等于八，那么 k 等于正负八。 好，那么所以这个 k 有 两个答案，当 k 大 于零的时候，就是 k 就是 八。那么解析式就是， y 等于 x 分 之八，当 k 为负值时，当 k 小 零时，也是 k 等于负八， y 就 等于 x 分 之负八。由于它没有告诉 k 的 正负，所以 k 有 两个答案都可以。那么这就是反比例函数的所有知识点，你学会了吗？拜拜。

hello， 大家好，今天我们来讲解二次函数这个专题， 二次函数呢，可以说是初中数学最难的知识点之一，想要学好二次函数呢，首先呢必须需要把一次函数学习好， 所以如果你看到这个章节呢，一定是先把一次函数那个章节看完之后你再来看这个章节，因为它跟一次函数是有很强的关联性。那我们来讲解二次函数的知识。 首先呢，我把二字函数的制框架全部列在这里，做了一个思维导图，我们一起来看一下二字函数的支点。首先第一部分定义及图像，这部分呢，内容比较简单，包括了定义图像，还有函数应用。 第二部分，二字函数解析式。这部分开始呢，内容就比较难了，首先它包括了函数的解析式，图像与性质解析式求解，还有最值问题。 前面四个小章节呢，相对来说比较简单，但是从第五个章节含餐的解析式难度就比较大了，它包括了二次函数含餐问题，二次函数含餐最值问题， 还有区间边界含餐的最值问题，还有函数也含餐，边界也含餐，它的最值问题以及第五小节呢，内容是非常非常重要的 啊。第六小节，一元二次方程，第七小节，第八小节包括了这个一元二次不等式和不等式的逻辑，这里面就详细给大家介绍什么情况下是都有 或者是总有，那什么情况下是存在啊，这样的话到底应该怎么理解，怎么去解析是非常非常重要的。那第九个章节是咱们整个第二大章节的最难的部分，叫做含餐区间比大小， 两个含餐区间如何比大小，一个含餐区间跟一个含餐值如何比大小等等这类的知识点 啊，中考呢，经常会在这上面出真题，所以呢，第九部分大家一定要把它真正的学深悟透 啊。第十部分呢，是一个二字函数的这个切线，它是一个了解部分，那我们再来看一下。第三大部分，叫做二字函数与图像结合， 大家通过这张图也能看出它内容是不是非常多呀。第一部分，图像变换，这部分跟一字函数类似，原理是一样的。那第二部，多函数的结合与一字函数与反比例函数结合都有哪些知识点 啊？第三部分，线段最直，那这部分内容呢，非常重要，这部分呢，我会讲直线线段怎么求，斜线段怎么求，线段笔直怎么求？和差怎么求。第四部分，面积问题和第五部分，存在性问题，这个我们在一字函数当中已经讲解过了，所以这部分呢，就讲一些例题。 那第六部分，函数跟几何结合，那这个也是非常重要的一个部分，包括了全等三角形相距，三角形角平分线、角度平行垂直等等这类的问题。第七小节二次函数十五问，还有第八小节常见的二次函数 啊。第四大部分呢，是二字函数的一些创新题，包括了规律探索、函数新定义、函数动点最值以及函数探究类问题。那第五部分呢，主要是考察大家对前面所学的知识是不是掌握了， 我会准备几道中考真题让大家去训练一下。好了，废话不多说，开始整个二次函数的讲解，那第一个章节就叫做定义及图像， 那我们先来看一下二次函数的定义，说一般如果 y 等于 a 倍的 x 平方加上 b， x 再加上 c， 这里的 abc 都是常数，而且 a 不 等于零，那么 y 就 叫做 x 的 二次函数， 这就他的一个定义。那这里需要注意的什么？第一个就是自变量， x 的 取值范围为全体实数，而且最高次是二。第二个是 a 是 二次项系数， b 是 一次项系数， c 是 常数项。 大家在写系数的时候，一定要包括前面的符号，有的时候大家经常会把这个符号负的符号给拉掉，这里一定要注意。第三个也是非常重要的，叫做 二次函数系数 a 不 等于零，这个呢非常非常重要，因为有的时候题目给你的一个这样的表达式，但是它没说是二次函数还是一次函数，所以说你就要分类讨论。 a 等于零的情况下，它是一次函数， a 不 等于零的情况下，它是二次函数。 好，那这个就是基本的定义，我相信这个呢也比较简单，那我们来看一道例题，说如果 y 等于 m 减二倍的 x 的 m 的 平方减去 m 方，关于 x 的 二次函数，则 m 等于多少？首先我们看一下题目，告诉我们这个是它是一个二次函数，那么系数肯定是 不能等于零，同时呢，最高次是不是只能等于二啊？所以这里面隐藏的应该是两个条件，一个是 m 的 平方减 m 等于二，另外一个是 m 减二，要不等于零，所以一定要注意不等零的情况，所以就会觉得 m 等于负一，所以选 a 这道题比较简单，考察你对定义的理解。那我们再来看下这道题，说，若函数 y 等于 a， 减一倍的 x 平方减去四 x， 再加上二 a 的 图像与 x 的 轴有且只有一个交点，则 a 的 值等于多少？ 很多同学一看到这个于 x 之后只有一个交点，我令它的第二它等于零就 ok 了。如果你这样写，那这道题就做错了。首先我们先看一下题目，他说什么？若函数 说是二次函数了吗？没有，虽然它长得非常像二次函数，但是没有说是二次函数。所以你这时候就要分类讨论，它是二次函数还是一次函数。如果是一次函数，那它跟 x 轴肯定只有一个交点。那如果是二次函数呢？是不是第二，它等于零的时候只有一个交点？ 所以呢，大家千万不要忽视 x 平方前面这个系数，所以这里一定要分类讨论。 a 不 等于零的时候，它是二次函数， a 等于零的时候，它是一次函数。 所以呢，这道题呢，最终结果它是有三个值，负一、二或者是一。如果你漏掉了一种情况，那这个题就不能拿满分了。好，那这个就是这道题。 第二小节我们来看一下这个二次函数的图像，那二次函数的图像是一条关于某条直线对称的 曲线，叫做抛物线。抛物线是不是更形象一点，我们抛一个物体，它是不是是这种轨迹啊？所以我们就把二次函数叫做抛物线，那条直线就叫做什么对称轴，对称轴与抛物线的焦点叫做抛物线的顶点。大家看下面这两张图， 是抛物线，有的时候开口向上，有的时候开口向下，但是他肯定都有对称轴，都有顶点。说到这了，那我是不是就得再拿出这张图啊？这张图我是不是在反比例函数当中讲解过啊？看看不管是圆还是椭圆，还是抛物线还是双曲线， 双曲线里面又包括反比例函数，它都属于圆锥曲线。所以说呢，咱们现在所学的抛物线或者二次函数，它也属于圆锥曲线当中的一部分，等我们到了高中，这些曲线都会学到这里呢，大家只需要了解一下， 经常会有二字函数的应用，那我们在生活当中，我们经常会遇到与二字函数以及图像相关的问题，那解决这类问题的思路是什么？首先第一个，我们先要读懂题意，弄清题目当中牵连了几个量的关系， 并且建立适当的绩效坐标系。第二个呢，在根据题目当中的已知条件建立数学模型，这里也就说的是建立函数关系式，也就是 y 等于多少倍的 x 这么一个关系式。 那第三个部分呢，我们再利用数形结合的思想，去利用函数的性质解决实际问题，比如说几何图形当中的最大面积问题、 商品利润最大化、拱桥问题或运动轨迹，这些都是二次函数的一个实际应用。那这部分题型呢， 我相信在以后中考改革当中，占比会越来越多，他需要你既要学会二次函数的基本理论知识，同时还会解决实际问题。这里面呢，还有一个有趣的现象，经常我们解决实际问题的时候呢，后线的开口啊，都是向下的， 为什么？因为在实际生活当中，基本上都会有最大面积利润最大化，那就说明他肯定是有一个最大值，所以呢，开口方向一般都是会向下，所以实际问题当中的二次函数大部分的开口都是向下。好，那这个就是函数的应用， 那我们具体来看一道例题，二零二四年泰安的中考阵地说如图，小明的父亲想用长为六十米的栏杆，再借助房屋的外墙围成一个矩形的菜园，已知房屋外墙长四十米， 则可围成菜园的最大面积是多少平方米？那我们是不是就可以设，比如说这个是 x， 这个是 x， 这个就是六十减 x 面积的呢？是不是就等于 x 乘以六十减去二 x， 但是呢，这么一个条件说这个外墙为四十，是不是不能比四十大呀？好，那也就是说明六十减去二十是不得小于等于四十，当然它肯定也是大于零的。 如何解？这个 x 一 是不是等于零啊？ x 二呢？是不是等于三十啊？好，那这个抛物线是，我是不是就大概可以画出来了？ 它经过原点，经过三十，好，那对正轴是多少？是不是就是十五呀？ 那十五的时候是不是去掉最大值，所以最大值就是十五乘以六十减去二倍乘以十五就是三十，代表是不是等于 四百五呀？好，那我是不是还得检验一下，那是不是满足这个条件呀？ x 等于十五、十五、十五，那这等于多少？是不是等于三十？三十是不是在零的四十中间啊？所以没问题，答案是不是就是四百五呀？那我们来看一下这个答案最终是不是就是四百五呀？好，这道题呢比较简单。