两个笛卡尔积如何制作
广义迪卡尔基是指数学中两组 x 和 y 的迪卡尔基,也叫直击,表示为 x 乘 y。 第一个对象是 x 的一个成员,第二个对象是 y 的所有可能的有序对中的一个设大合并为一个集合,以二中的元素为第一个元素, b 中的元素为第二个元素,两个元素构成有序队。所有这些有序队都有一组称为 r 和 b 的迪卡尔基,并记录为 r 乘 b, 二乘以 s。 十一个木关系, 前恩列是关系二的属性,后恩列是关系 s 的属性。每个元组的前恩个属性是关系二的一个元组,后恩的属性是关系 s 的一个元组。两队游泳运动队均有三名队员组成,现做循环比赛。赛事表可看成是两队名单的广义迪卡尔基。
粉丝3.0万获赞48.0万
相关视频
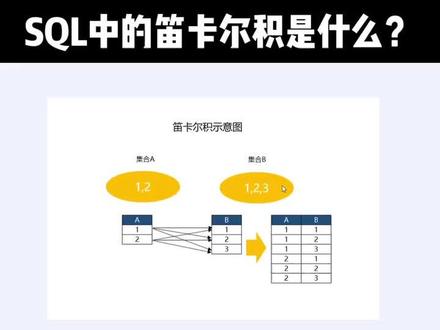 01:00查看AI文稿AI文稿
01:00查看AI文稿AI文稿哈喽,大家好,我是李月,今天给大家讲解一下迪卡吉。迪卡吉呢是我们在数学上的一个概念,它是指两个集合的其中 a 一个元素与另外一个集合的元素进行两两组合。 那么在我们的数据库中,他是怎样的一个表现形式呢?比如说我们这里有一个表 a, 我们可以把它看成一个集合,然后表 b 也可以把它看作一个集合。当我们要执行低卡耳机的时候呢,可以直接使用 costoree, 然后就可以得到他们的低卡耳机了。 迪卡基呢是我们之后要讲解了脚印的所有观念的基础,不管是左观念还是右观念,都是以迪卡基为基础来进行观念关系的。
227SQL数据库开发 00:51查看AI文稿AI文稿
00:51查看AI文稿AI文稿当工作与爱情相遇,马上跨年了, excel 给的浪漫你会吗?猴哥教你,你先在 a 二单元格输入 x, 然后在 b 二单元格输入 y, 用来代表坐标轴 x 下方输入负一点八一, 点击填充,选择区列,把行改成列,不长值改成零点零一,中指值改成一点八一,确定。然后在 y 下方输入我们准备好的函数,双击右下角向下填充,接着点击文件,打开选项, 点击公式,在计算选项里勾选叠带,计算叠带次数改为一,确定 c 二单元格,输入等于 c 二,加零点零五,选择前两列数据,点击上方插入,插入一个散点图,调整下大小, 删除散点图中多余的内容,换成自己想要的颜色。最后我们按住 f 九新型曲线图就动起来了,能不能学会啊?能能能!
14.1万Excel办公秘籍 00:34查看AI文稿AI文稿
00:34查看AI文稿AI文稿迪卡尔基啊,他是将这个表里面的呃,每一行跟这边呢相互结合,比如 a 零 f 三 k 二,然后呢再跟 a 零 n 二 x 一啊,然后呢这个 b 一呢也是一样的,再跟他,再跟他,然后最终就得到了这样的一个大表。那这种呢就通过迪卡尔基啊,这两个他是有一个规律的,就是说 他的列数啊,加上 s 的列数,等于最终这个的列数,他是不是两列?这边是三列,这边是五列,这种呢叫做几卡几的运算,他这个是两行,这个是两行,他的行数其实是相同的关系,对不对?因为这个要分别跟他的每一行去进行运算,然后这一行要跟每一行运算,所以他两个的行数相乘,就是得到最终的这个行数。
244快去学计算机二级 00:51查看AI文稿AI文稿
00:51查看AI文稿AI文稿用 excel 制作迪卡尔爱心,你会吗?十秒教会你!你先在这这个单元格输入 x, x 下方输入负一点八一,点击编辑,点击填充,选择序列,勾选列不长值改成零点零一,中指值改成一点八一,点击确定。接着在这个单元格输入 y, 在外下方输入这个函数,函数放在评论区了,然后双击右下角向下填充,在 c 二单元格输入等于 c 二加零点零五,接着点击文件,点击选项,点击公式勾选起,用迭代计算,迭代次数改为一,点击确定,再选择前两列数据, 点击上方插入,插入一个散点图,调整一下大小,删除散点图中多余的内容,再把散点图换成自己想要的颜色。最后我们按住 f 九爱心曲线图就动起来了,你学会了吗?关注我,每天学习一个 excel 技巧!
1682小俊excel 01:36查看AI文稿AI文稿
01:36查看AI文稿AI文稿迪卡尔,爱心属于 excel 的 浪漫,你会吗?今天一分钟教会你!第一步,新建一个空白 excel, 在 a e 输入 x, b e 输入 y, 然后在 a 二输入负一点八一。 第二步,选中 a 二单元格,点击开始菜单栏选择填充,选择序列,在序列产生在列不长值填写零点零一,中指值填写一点八一, 点击确定,这样就自动生成了一列范围在负一点八一到一点八一的等差序列数。 第三步,在 c e 单元格中输入公式等于 c 一 加零点零八。第四步,在 b 二单元格中输入以下公式,然后双击填充。第五步,点击文件,点击选项,点击重新计算, 勾选迭代,计算最多迭代次数填写一,意思是有关循环引用最多迭代的次数为一次, 点击确定。第六步,选中 a 列和 b 列,选择插入,选择散点图,选择这种平滑的散点图,点一下散点图,然后将图标元素勾选全部去掉,同时将颜色和轮廓都填充为红色。 第七步,见证奇迹的时候到了,一直按 f 九,意思就是刷新重新计算,可以看见 c e 和 y 列数据一直在重新计算,也可以看见散点图,慢慢变成爱心了。元旦快乐,每天开心快乐送给大家哦!
49红姐办公 00:52查看AI文稿AI文稿
00:52查看AI文稿AI文稿很多人说按住 f 九不动,我给大家说几个原因,可能的原因哈,一个是这个格子要输 他同一行的,比如说这是在 c 二,就是 c 二加上零点一,或者是零点零五,或者是你想要的数啊,零点几都行,我觉得零点一最好看。嗯,然后这个外折的公式待会我再发给大家一下。还有一点就是大家 这个一定要去勾选迭代计算, 还有就是这个一定要下拉呦。第二,公式输了之后要双击他,我刚才就是没有双击这个,还有一直按住 f 九哦,不要松哦,如果都按照我说的这样子操作了,还是不能动的话,欢迎评论区告诉我,我给你们看看是怎么回事。
 01:38查看AI文稿AI文稿
01:38查看AI文稿AI文稿全网火热的迪卡尔爱心不允许你不会,快去学习一下吧!在同事面前露一手!点击 a 一 单元格,输入 x 回车,输入负一点八一,点击负一点八一单元格数据填充序列, 选择列不长值零点零一中指值一点八一确定。 点击 b 一 单元格,输入 y 回车。在 b 二单元格输入以下公式,回车,双击向下填充 点 c 一 单元格,点文件选项重新计算,选中迭代,计算最多迭代次数,输入一确定 c 一 单元格,输入等于 c 一 加零点零五, 选中 a、 b 两列,点击插入 散点图, 调整合适的大小,删除多余的元素,右键散点,填充红色 轮廓,红色按住 f 九刷新。你学会了吗?关注我,每天进步一点点!
5374辉姐办公技巧 02:05查看AI文稿AI文稿
02:05查看AI文稿AI文稿数学家比卡尔与解析几何的故事。比卡尔将几何坐标体系公式化而被认为是解析几何之父。在他之前,几何是几何,代数是代数,他们各自为证,互不相扰。 但是传统的几何过分依赖图形和形式演绎,而代数又过分受法则和公式的限制,这一切都制约了数学的发展。 有一天,一位年轻的军官突发奇想,能不能找到一种方法架起沟通怠速与几何的桥梁呢?这位年轻的军官就是迪卡尔,这个问题苦苦折磨着他,在没有战士的军队中,他常常花费大量的时间去思考他。 十一月的一天,他因病躺在了床上,无所事事的他又想起了那个折磨他很久的问题。 天花板上,一只小小的蜘蛛从墙角慢慢的爬过来,土司结网忙个不停,从东爬到西,从南爬到北, 要结一张网,小蜘蛛该走多少路啊?迪卡尔就开始想如何去算蜘蛛走过的路程,他先把蜘蛛看成一个点,那么这个点离墙角有多远呢?离墙的两边多远?昏昏沉沉的他思考着计算着,病中的他又睡着了。 梦中他好像看见蜘蛛还在爬,离两边墙的距离也是一块大些,一块小些,他好像悟出了什么,又看到了什么。大梦醒来的迪卡尔茅塞顿开,要是知道蜘蛛和两墙之间的距离关系,不就能确 定蜘蛛的位置吗?确定了位置后,自然就能算出蜘蛛走的距离了。 于是他郑重的写下了一个定理,在互相垂直的两条直线下,一个点可以用到,这两条直线的距离也就是两个数来表示,这个点的位置就被确定了。
147数学思维 01:16查看AI文稿AI文稿
01:16查看AI文稿AI文稿天下没有不散的宴席,这个视频是猴哥今年最后一个作品了,关于二六年,猴哥没有什么好送给你们的,就送给你们一个 excel 最终的浪漫吧,感谢你们这么多年的陪伴, 猴哥教你一招。首先咱们在 a 二单元格输入 x 坐标轴, b 二输入 y 坐标轴,然后在 x 坐标轴下面输入负一点八亿, 然后点击这个单元格,点击编辑,点击填充,选择序列,序列产生在列,然后不长值是零点零一, 中指值设为一点八一,然后确定在 y 坐标中,下面输入咱们的公式,这个公式已经放在了评论区,然后双击右下角填充,随后点击文件,点击选项,选择公式,勾选,启动迭代计算,最多迭代次数改为一,然后确定 之后在 c 二单元格里输入等于 c 二加零点零五,选中 a b 两列,点击插入,插入散点图,选择第二个,然后调整一下大小, 点击加号,把打勾的都给取消掉,最后可以更改一下自己喜欢的颜色,然后按 f 九就可以实现爱心的滚动效果了,你学会了吗?最后猴哥预祝所有粉丝们新年快乐,在二六年,猴哥的作品也会像这个爱心一样充满活力!
8595猴哥讲办公 02:27查看AI文稿AI文稿
02:27查看AI文稿AI文稿但如果真的爱 过,总是才 明白你的 悲。我知道爱。
557是小朱(实习生版) 00:21查看AI文稿AI文稿
00:21查看AI文稿AI文稿看好了,全网爆火的迪卡尔爱心函数制作教程和现成的文档,书包已经整理好了,不会用 excel 的 宝字,可以用现成的文档直接运行,下面跟我操作教你获取。首先点视频右下角分享,点分享链接, 接着返回桌面,打开这个工具箱,打开后等两秒会弹出文件,点查看找到迪卡尔爱心函数,保存下载就可以使用了。
11Kitty 02:04查看AI文稿AI文稿
02:04查看AI文稿AI文稿录一个上一个视频火的迪卡尔心形函数教程,我为了美观呢,我会给他们都全选一下,然后选这个居中,这样会好看一些。在 a 一 单元格这里输入大写的 x, 在 b 一 单元格这里输入大写的外在 a 二单元格,也就是 x 的 下面,这里我们输入负一点八一 好,敲回车键这里我们一定要选中回来,点右上方的填充,这里有一个序列,点击这个列,把这个不长值改成一点八一,点击确定 好的,填充好了,填充好之后,我们在 y 的 下面就是 b 二单元格这里点一下,点完之后在这里输入直直接 ctrl 加 v 粘贴一下这个公式,待会我我会把这个公式放到评论区好,粘贴好之后,我们敲下回车键,确定 再点回来,鼠标放到这个右下这个绿框的右下方这里双击鼠标左键就可以都给他填充上了。填充好之后点左下方的文件,这里有个选项,点击选项找到重新计算,把叠带计算给他勾选项,这个最多叠带次数改成一好。点右下方的确定 在 c 一 单元格这里,我们输入大写的啊,输入等,先输入等于再输入大写的 c 一 加 零点零八或者零点零五也行。敲回车键,确定完事以后,我们把 ab 两列给他俩同时选中,选中之后就按住鼠标左键从左往右这么一划就行。点上方的插入这里一个图标, 选择三点图里面的第一个。好,我们,呃,为了让这个爱心美观一些的话呢,我们可以把它变方一点,这样的话那个爱心会更饱满一些, 这样去拖拽就可以。好,选中这个线条,先把颜色改一下,填充这里改成红色,轮廓这里改成红色或者其他的颜色,粉色、蓝色都可以,紫色什么都可以,你喜欢什么颜色就改什么颜色。再把这个 s 角、 y 轴都改删掉,选中它们之后一定要点上这个数字,选中它们之后点键盘上的的的键,删除 都给它们删掉,删完之后长按 f 九它就可以动起来了。如果你按完 f 九之后还没有动的话,那你就 fn 加 f 九, fn f 九一块按就可以了,是不是很浪漫呢?赶快做起来吧!
2408Coco 01:29查看AI文稿AI文稿
01:29查看AI文稿AI文稿利用一个函数制作这样的动态爱心,首先在 a 二单元格中输入 x, b 二单元格中输入 y, 表示两位坐标轴, 在 x 下方输入负一点一八,在开始菜单里面点填充,点击序列,选择列不长值,输零点零一中指值一点一八确定, 在 y 下方输入这个公式回车,双击十字加号填充,在 c 二单元格中输入于 c 二加零点零五回车。接着点击文件选项公式, 勾选起,用迭代计算,将次数改为一确定, 再选中 app 两列,击插入散点图,把里面的数字全部删除, 将线条改成自己喜欢颜 色。最后按键盘上的 f 九动态爱心就制作好了, 然后可以开心一整天了耶!
1489颜 02:27查看AI文稿AI文稿
02:27查看AI文稿AI文稿单元格输入 y a。 三、单元格输入负的一点八一,填充序列,列不长值零点零一,中指值一点八一,确定 y b。 二、 b。 三,输入一个函数公式,双击填充,选择文件选项,重新计算,迭代计算最多迭代次数。一,最大误差零点零零一,确定 c r, 单元格输入 c r 等于 c r, 加零点零五,确定全选 a b 两列,插入三点图,可以调成一个大家喜欢的大小 填充红色,全部框选成红色,然后按长按 f 九, 为了好看,也可以把背景选成粉色,然后填充无填充颜色轮廓,无边框、 坐标轴、图标标题网格线, 线条选择无线条。 嗯,然后这样一个 dakar 的 爱心就好啦!
840我叫 张富贵 22:08查看AI文稿AI文稿
22:08查看AI文稿AI文稿好,我们开始讲第七章啊,第七章,第七章呢,是 二人关系,那么他在结合论当中是比较重要的一个内容啊,那么第七章的主要内容有包括有序对,迪卡尔乘机。那么二人关系的定义已表示法, 那么关系的运算,关系的性质,关系的必包,等价关系划分,平息关系,这些我们都是要讲的啊,都是要讲的。 今天我们来讲一下这个游戏,对以迪卡成绩以及二人关系的这个表示啊,二人关系定义表示。 好,首先我们来看一下什么是有序对啊?什么是有序对, 有两个元素 x, y 按照一定的顺序组成了二元组,那么称作是有序对啊,有序对,那么这里呢,有两个,这个 keeppoint 是吧?关键点,一个是顺序是吧?一个是有顺序的。第二就是二元组啊,有顺序的二元组, 那我们把它称作是一个有事以对啊, 那么有序队呢?是用间括号来括起来的啊,有序队啊,那么有序队一个是有顺序性是吧? 第二个就是如果两个有序对,如果相等的话,就是,那么前面两项相等,后面两项对应的两项相等。嗯, 好,我们来看一下 decal 乘积啊,设 a b 为集合 a, 以 b 的 decal 乘积即做 a 乘 b, 且 什么呀,写什么呀? a 成 b 的元素都是什么呀?都是有序队啊,那么有序队的这个前前进是吧?有序队的前进来自于 a 集合 a 集合的元素,那么有序队的后键呢?是来自于 b 集合的元素啊,那么这个程度是有序队。呃呃,迪卡尔成绩是吧。所以呢,迪卡尔成绩其实就是什么呀?就是有序队的啊,集合,那么这个有序队呢,是由 a 集合里面的元素和 b 集合里面的元素共同组成的啊,这个底杆成绩在以后大家学数字库里面啊,数字库表的这个 内程啊,也会内程,其实也是这个 d k 二乘机啊,数据库表的内程啊,内连接。好,我们来看一个例子啊,看一个例子, 那么是 a 是这个一二三集合, b 是 a b c 集合啊,那么 a 乘 b, a 乘 b 就是什么呀?就是 a 乘 a e b 的第二成绩,是吧?那他其实是有序队的集合啊,那么有序队的前键是来自于 a 的是吧?那就是一 a 一 b 一 c 啊,那就是前键 是来自 a 是吧?后键是来自于 b 集合啊,那么二 a 二 b 二 c 三 a 三 b 三 c 啊,就是这么一个有序类的集合,那么 b 乘 a 呢? b 乘 a, 就是这个 b 集合里面,是吧?先由 b 集合里面组成的元素啊,那么是由构成前键,那么 a 集合的元素呢?是来构成这个后键啊,然后组成这个游戏队的一个成绩啊,就这样。 好,我们来看一下这个啊, a 呢,是等于空级的几和 b 等于空级,那么 p a 乘 a 是吧?首先我们要看一下 p a 等于什么是吧? p a 等于什么啊?那么 p a 应该是 一个是空级,是吧?空级是一定要有的,是吧?空级。另外还有就是什么呀?这是零个元素,那么还有就是一个元素的集合,一个元素就是什么呀?空集的集合,是吧?这是一个集合的元素,那就是他自身啊, 那么这是这个 p a, 那么 a 呢? a u 是等于这个空级的几何的是吧?那么 p a 乘 a 就是什么呀?诶?由这里面拿一个元素出来,是吧?空级, 然后这里面拿个元素出来啊,这也是什么呀?这也是空级啊,这样组成游戏队,然后这里面其实还有个元素,是吧?那就是空级的 集合,然后再次空起啊,这样啊,那就等于这个,是吧?等于这个 啊,好,我们看一下 p a 乘以 b, p a 等于这个,是吧?等于空集和空集的集合的这个集合,那么 b 集合呢? b 集合是空集,空集是没有元素的,所以呢?没有元素是, 所以他当然也没没办法拿拿这个元素出来去构造这个游戏队,是吧?所以呢, p 这个第二成绩,第二成绩里面,如如果 a 和 b 呢?前面和后面呢?有一个是空级,那么他整个就是空级啊。 好,我们看一下 decar 成绩的性质,第一,它不适合交换率,是吧?不适合交换率,因为什么呀?因为 decar 成绩它是有序对的即可。有序对是什么呀?有序对是有顺序的啊, 所以他对这个顺序是非常敏感的啊。第二,他不适合结合率啊,不适合结合率,因为你如果要结合的话,那么他 他们结合之后的他的这个有序队是完全不一样的啊,完全不一样,所以呢,就是这个风,这个是不一样的一个这个有序队啊,所以他也不满足这个结合率。 那么第三,对并应省或者交应算啊,还有集合的应算呢,它是满足分配率的。 那么迪卡尔成绩与并级和交集其实是两个维度啊,两个维度的这个运算,所以呢,他当然就可以这个满足这个分配率啊。所以好。第四, a 和 b 当中有一个如, 如果是空级的话,那么他们的 decar 成绩就一定是空级啊,一定是空级, 这个刚刚我们已经已经这个做过了,是吧?好,第五个,如果 a 里面 a 集合里面有 m 个元素, b 集合里面有 n 个元素,那么 a 乘 b 抵考成绩的元素就是什么呀? m 成 n 的,是吧?因为什么呢?它有 m 中可能,是吧,取值的可能,它有 n 中取值的可能,那么它们构成了有序列的取值可能就是 m 成 n 的啊, 这个证明我们就不证了啊。好,接下来我们来看一下这个恶言关系啊,恶言关系,那么恶言关系 呢?其实这个定义啊,其实他是一个,嗯,我们来看一下他的定义啊, 如果一个集合,他是空集,或者呢,他他的元素都是有序,对啊,那么他这样的一个集合称作是一个二元关系, 这里说明什么呀?说明空级也是一个二元关系,是吧?如果他不是空级呢?那么他的元素必须是什么呀?二元二元组,是吧?有序,对啊,有序,对,那么这样的集合呢?称作是一个二元关系。二元关系。 好,我们来看下这个实力啊,那么这是一个集合,是吧?这是一个集合,那么这里面的元素都是什么呀?都是有序, 对,所以呢,它是一个二眼关系啊,这个 s 集合呢? s 集合呢?这里有一个游戏队,是吧?但是这个 a 和 b 不是游戏队,所以呢,它不是一个二眼关系啊,它不是一个二眼关系啊, 那么这就是这个恶言关系的定义啊。他要么是空级,是吧?如果他不是空级呢?他的元素必须什么呀?都是有序队啊,一定要都是有序队啊,不能出现其他的这个情况啊。 好,我们来看一下这个 a 到 b 的关系与 a 上的关系是 a b 为几何?那么 a 乘 b 的任何子级所定义的二元关系叫做什么呢?叫做 a a 到 b 的二人关系,是吧?也就是说 a 乘 b 的任何子级啊, a 以 b 的底卡儿乘积是吧? a 以 b 的底卡儿乘积,都是什么呀? 都是有序队是吧?都是二元二元这个二元这个组有序队啊,有序队,所以呢,他的子级呢?当然也是有序队的啊,所以呢,这个集合呢,就称作 a 到 b 的二元关系,当 a 等于 b 的时候呢,就称作 a 上的二元关系,是吧? a 上的二元关系就是 a 乘 a 啊, a 乘 a, a 乘 a 的这个自积啊。好,我们来看一下这个 a 等于零一集合, b 等于一一二三集合,那么我们看一下,这里有 r 一 r 二, r 三、 r 四,是吧?好,我们看一下这个, 我们看一下 r 一 r 一零啊,有个零二,是吧?二肯定是从这来的,是吧?零肯定是从 a 来的,所以呢, r 一肯定是 a 到 b 的关系啊, a 到 b 的关系, r 二呢? r 等于 a 乘 b, 那么 r 等于 a e b 的低个儿乘积就是什么呀?这个肯定是,是吧?肯定是 a 乘 b, 肯定是这个 a 乘 b 的子级啊,所以呢,它也是什么呀?它也是这个 a 到 b 的关系啊, a 到 b 的二人关系,那么 s m s n 等于空级,空级是任何几何的子级是吧?他肯定也是这个这个 a 乘 b 的子级啊 啊, r 四呢? r 四零一是吧?零从这里取一个,一从这里取个,肯定也是这个啊,可能也是这个,所以呢, r 一 r 二, r 三 s 四都是 上面都是 a 到 b 的关系啊,都是 a 到 b 的关系,那么 r 三和 s 四这个稍微有点特殊啊,稍微有点特殊,为什么呢?因为他也是 a 到 a 的关系 啊,你可以把这个这个 b 集合给给盖住,是吧?那么空级肯定是 a 乘属于 a 乘 a 的啊,空级肯定属于 a 乘 a 的,那么零到一的集合呢?零到一的集合呢啊,零到一的这个游戏队其实也是什么呀?也是 a 乘 a 的集合,所以这个 r 三 r 四也是 a 上的二元关系。 好,我们来看一下这个二人关系的这个技术啊,技术,那么假设啊,假设 a 有 n 个元素啊, a 有 a 有 n 个元素,那么 a 乘 a 肯定就会是这个 n 的平方个元素,是吧? a 乘 a 是 a 的皮肤跟元素,这个就是什么呀?这个就是有序,对啊,有序对,有序对集合的这个个数,是吧?有序对集合的元素个数,那么 a 乘 a 的子级有多少个呢?有多少个呢? 子级的个数,这个就是什么呀?前面我们讲过,是吧,其实就是你 p 就是求密集,求的是, 我们之前讲秘籍的时候讲过,是吧?你要求一个集合的秘籍,其实就他求他子级啊,求他子级,所以呢, a 乘 a 的子级呢?就是有多少个呀,就有二的 n 的平方个啊,因为我们前面讲了,是吧,如果 a 有 n 个元素,那么他有多少个秘籍啊?那就是二的 n 字方个秘籍啊, 它的面积有二的 n 字方格元素啊,所以呢,这个也是同样的,是吧?所以呢, a 上有二, r 的 n 次方, r 的 n 平方个啊,二零,二零关系。 好,我们来看一下几个比较特殊的关系啊,特殊的二元关系,第一个就是空级啊,那么空级是任何几何的子级,是吧?所以空级呢,也是一个这个很重要的二元关系,我们把它称作是一个空关系。 第二就是权益关系,权益关系就是最大的这个,哎,这个集合是吧, 就是最大的这个 a 乘 a 啊, a 乘 a 里面最大的就是他自身啊,这个就是 a 乘 a, 所以他就是一个权益关系啊,就是所有的这个律师队都包括在里面了啊,第二个就是恒等关系啊,第二就是恒等关系。 横等关系就是什么呀?就是这两个有序的元素啊,是相等的啊,相等的,那么这个元素来自哪里呢?来自于 a 集合啊,来自 a 集合。 好,接下来就是小于等于关系,小于等于关系就是什么呀? x 小于等于 y 啊, x 小于等于 y 小等关系, x 小等于 y, 那么整除关系呢?就是 x 整除以 y, 是吧?整除以 y 包含关系,那么就是 x y 的子级啊, x y 的子级,那么这里签名是什么呀?证明 x y 都是都是几何啊,都是几何,那么 a 是几何的几何了啊, 好,我们来看一个例 子啊,看一个例子,那么 a 是等于一二集合啊, a 等于一二集合,那么 ea 等于多少呢? ea 就是这个 a 乘 a 的所有的可能性,是吧? a 乘 a 啊, a 乘 a 所有的这个可能性,那就是一一一二二一二二,是吧? 那么 i a 呢? i a 就是 x 等于 x, 是吧?一等于一二等于二,是吧?二等于二,这样的,这个就是 i a 啊。好,我们看一下,这个 a 等于一二三 b 等于这个 a b 啊, a b, 那么其实这里面讲的都是什么?都是 a 上的关系,所以这个 b 呢?没有任何,没有任何作用啊,还是这个 a 啊,那么 l a 呢?就是小于等于关系,是吧?那就是一 一一一二一三二二二三三三,整除关系啊。 d a, 那就是一一一二,是吧?一三二二三三啊,这就是整除关系。 好,我们看下这道题,这道这个例子啊,这个例子,那么 p b 等于什么呢?那么 a 等于 p b 啊, 这个 p b 就是 b 集合的密集,是吧? b 集合的密集,那么这个密集呢?是这个 b 集合从这儿来的啊,这个 b 集合啊,等于 a b, 那么密集就等于这个了,是吧?密集就等于这个,这个我们就不再细讲了。那么则 a 上的这个包含关系,包含关系呢?其实就是什么呀?哎,他就是一个有序队,是吧?有序队,二也有序队,那么有序队的话,前面是后面的元素的这个子级 啊,我们来个看一下空级,从空级开始,是吧?空级是空级的子级,空级是任何颜色子级,所以他有四个元素啊,一个、两个,三个四个。 好,接下来看一下 a 集合啊, a 集合应该有两个,是吧?一个是他自身,一个就是 a b 集合啊,一个是他自身啊,一个是 a b 集合, b 集合也是一样的,是吧?然后就是最后他这个 a b 集合, a b 集合只有他自身了啊, 这就是他这个包含关系啊,包含关系的这个这个奥运关系, 那么类似的定义呢?还有大于等于是吧,小于大于关系,真报案关系等等啊,好,我们来看 一下关系的表示啊,关系的表示,哎,就说给你一个恶言关系是吧,给你一个这个有时对的集合,你怎么样来表示他啊?你除了用集合的表示方法之外,其实还有两种更加形象或者是更加直观的表示方法 啊,一个是关系几证,一是关系几证,另外就是关系图几证,我们可能都在这个代数里面其实都学了,是吧,他是有行有列的啊,那么关系几证其实是不是一个特殊的这个几证,那么几几证里面的元素要么是零, 要么是一啊,要么是零,要么是一,那么这个零表示什么呢?零表示对应的行和列呢的元素是没有啊,没有有序,对的啊,如果是一的话,就是有有序,对,是吧? 对应的行和列是有存在,有序堆的话就是一,如果不存在就没有啊,就是零。好,我们来看一下这个 x l a 等于 x e, x 到 x m 是吧? y 等于这个, 那么 r 就是 a 到 b 的关系,那么这样的话,我们可以这样写啊,行是吧? x 就是行啊, x 一 x 二到 x m 啊,这就是 y 一 y 二到 y n 对应的啊, x 啊,我应该,我应该是这个写,我应该写反了啊,就是 x 在这里啊, x 在这里,这是 y 啊, 对应的 x 到 y, 如果有边的话啊, x 到 y, 如果存在这样的有序,对的话, x 一 y 一,如果是存在的话,它就等于一啊,也就这个地位置是一,如果没有就是零啊,没有就是零,这样的啊,这样的一个集镇,布尔集镇是吧?布尔集镇 好。第二个是关系图,关系图其实就是一个带有顶点和有向边的一个图啊,顶点,顶点就是什么呀?就是 a, a 的元素啊, a 的元素,那么边呢?边其实就是这个有序对,是吧?如果存在有序对,就是存在边啊。 那么从这两个这个定义我们可以看出 a 关系矩阵,它好像可以表示这个功能更强大一些,是吧?关系矩阵可以表示 a 到 b 的关系,也可以表示 是 a 上的个关系,那么关系图呢?关系图只能表示什么呀?只能表示 a 上的关系啊,只有一个 a, 是吧?没有 b 集合,这里呢?有 a 集合,有 b 集合啊, 这个就是这个关系的表示。我们来看一个例子吧,我们来看一个例子,那么 是 a 是,是 a 等于一二三四啊,是 a 等于一二三四,那么 r 等于一一,是吧?一一一二二三 啊,四四二,那么 r 的这个关系起见就可以这样来表示,是吧?我们可以这个 x 一 x 二,是吧?那就是一二三四,这也是一二三 三四。那么如果是 a 上的关系,那个关系之间就是什么呀?就是一个有这个行和列相等的一个行,行数和列数相等的,是吧?好,我们看一下,一一有边,一一有边,就这里是一,是吧?一二有边,这里是一, 然后呢?这一行就没有其他的了,这没有的话就是零零啊,然后二打头的, 二打头的有二三二四,是吧?二三二四没有,其他的没有,其他的用零来表示啊,好看。三打头有没有?三打头?没有啊,没有,就是零啊。 啊?我们看一下四打头的,四打头的只有四二,是吧?四二在这,其他地方都是零啊。好,这就是什么? 这个就是这个,这个关系取证啊,关系取证。好,我们来看一下关系图,关系图。哎,这里有一二三四四个顶点,是吧?这是零啊,一二 三四啊,那就是一到一有这个边,那就是他自身的顶点上的坏了啊,这个是一到一的边,一到二的边啊,这个然后是二到三的边,二到三这里啊, 然后呢?二四四二,是吧?二四四二啊,这样的,这个就是关系图啊,这个就是关系图, 这个就是这个二人关系的这种两种表示法啊,两种表示法。 好,今天的这个我们课就讲这么多啊,那么接下来的时间大家做一下这个课后习题啊。大家翻到这个一百三十九页啊,做一下第十题啊,第十一题啊, 大家做一下这个 co 习题啊,一百三十九页。第十题和第十一题。
224世文
猜你喜欢
- 3479酷家乐也陌
最新视频
- 7814额,滚🙄




