粉丝801获赞7676
相关视频
 04:47查看AI文稿AI文稿
04:47查看AI文稿AI文稿各位同学大家好,我是研发国老师,今天呢,我们给大家录制一下这个抛物线切点弦方程的这一个推导过程啊。呃,后面呢,我们可能还会讲到这一个阿基米德焦点三角形, 那么上面呢,也有一些这个跟这个相关的东西哈,大家可以看一下。切点弦是指什么呢?可以看就是指这个呃,抛物线上的过抛物线外的一点呢?引抛物线的两条 这个切线,那么两个切点呢?连线的直线方程呢?我们称为千点线,那千点弦的这个直线方程怎么怎么解呢?大家看图中的信息呢,我们就已经标好了, 对吧?已经给大家标好了,那么呢,我们就主要由什么呢?由斜率的两种表示,斜率的两种表示, 大家看啊,对这个对直线 a p 来讲, 对 a p 来讲,那那么 k a p 等于什么呢? k a p 呢,它就等于 y 零减 y 一除以一个什么 x 零减 x 一,这就等于什么呢?哦, y 零减去一个。 哦, r p 分之 x 一方,除以一个 x 零减 x 一,对吧,又因为什么呢?这个是不是 y 等于二 p 分之 x 方, 所以 y 岛就等于什么呢? y 岛,它就等于 p 分之 x, 所以 k a p 呢,就等于什么呢? k a p 呢,它就等于 x e 除以 p, 则啊,则就有 y 零减二, p 分之 x 一方,除以 x 零减 x 一,等于什么呢?等于 x 一除以一个什么 p 交叉相乘可就是 p y 零。 注意哈, p y 零减二分之 x 一方,等于什么? x 零 x 一减去一个 x 一方。好,那么呢,我们乘再乘以一个二,它就有 则,这个就有 x 一的平方,这个呃,减去一个二 x 零 x 一加上一个二 p y 零 等于零,没问题吧?那同理同理,这个 x 二的平方减去 r x 零 x 二加上二 p y 零呢?也等于零,可知啊,可知 什么呢? x 一 x 二是方程, 是方程 x 方减 r x 零 x 加上二 p y 零等于零的连减。我来往这边移一下,啊, 等于零的两个减啊。啊,那么 右右什么呢? x 方等于二 p y 代入就是二 p y 减二 x 零, x 加上二 p y 零等于零,即 即这个 x 零 x 等于什么呢?必备的 y 加上一个 y 领,没问题吧,所以我们已经推导出了这个结果, 没问题吧,没问题吧?好,那么如果呢?我们思考哈,补充一下,如果啊,如果 是这个外方等于二 p x, 那么则七点弦 就是什么呢?就是 y 零乘以 y 等于必备的 x 加什么 x 零,没问题吧。好,那么这种推导呢,应该是一种比较简洁的推导方式。好,那我们把这个方法呢告诉大家,希望后面呢对大家理解这一类型的这个题目啊,有所启发和帮助。好,那么感谢大家的点赞和关注,谢谢大家。
246数学时光 01:20查看AI文稿AI文稿
01:20查看AI文稿AI文稿两句话,十秒钟,教给大家一个方法,求解切点弦方程,过点三一做这个圆的两条切线,切点分别为 a、 b, 求 a、 b 直线的方程是什么?第一句话,大家要记住, 先去确认一下这个点是不是在原外,并且求的是切点连线方程, 点在不在原外,直接带入到方程的左边三减一的平方,加一的平方明显大于一,所以点在原外。确定这个之后,第二句话,带一留一求切点的连线方程。 什么叫代一留一?咱们来解释一下 x 减一的平方,咱们可以把它看成 x 减一乘以 x 减一加上 y 的平方,可以看成 y 乘 y 等于一。 所谓的带一留一,就是把横坐标三带入到一个 x 减一里面,把纵坐标一带入到一个 y 里面, 所以这个式子就变成了三减一留一个 x 减一加上一乘以外等于一,整理这个方程。最后就是二 x 加 y 减三等于零,他就是切点连线的方程,大家学会了吗?
5653高中数学-李钰提分课堂 03:08查看AI文稿AI文稿
03:08查看AI文稿AI文稿这个视频咱来讲讲切线方程。比如这个圆,圆心是圆点,半径是二,那圆方程显然是 x 方加外方等于四。如果在圆上选个点一根号三吧。那我问你,过这个点且与圆相切的切线方程是啥? 这一简单连接圆心和切点,这个点是一根号三,那他的斜率就是根号三。这两条线肯定垂直,斜率成绩负一,那这条线的斜率就是负的三分之根号三呗。 有了斜率,又有个点,直接用点斜式写出方程,整理一下就是 x 加根号三,万减四等于零。你看用斜率和定点就可以计算切线方程,这是比较科学的算法。咱再来讲个不大科学的要求。这个圆过一根号三的切线方程,你只 只要把圆方程中的一个 x 换成一,一个 y 换成根号三就可以了,你看跟咱算出来的一样,所以只要把 x、 y 各换一半,就能得到切线方程。类似的,这个圆或根号二,根号二的切线方程就是根号二 x 加根号二, y 等于四。 那么问题来了,如果圆心不是圆点,比如这个圆过点一负四的切线方程怎么求呢? 嘿嘿,还是能用带一半的法子把这个 x 换成一,把这个 y 换成负四,这个方程就是你要求的切线方程啦。 怎么样,带一半的方法好用吧?那么问题又来了,如果点在圆外,比如这个圆和这个点,那按照带一半的原则,这么写出来的直线方程还是缺陷吗? 当然不是,他是这个点向远影切线,这两个切点连线的直线方程,这叫切点弦方程。看着好像很有道理,可是为啥呢? 假设这个缺点是 ab, 根据切线方程,这条线就是 ax 加 by 等于一,类似的,这个缺点是 cd, 那这条线就是 cx 加 dy 等于一。 这两条线的焦点是三二,那三二就符合这个方程就有三 a 加二 d 等于一,而且又符合这个方程是三 c 加二 d 等于一。 仔细看看这俩柿子是不是可以理解为有一个方程叫三 x 加二 y 等于一,而 ab 和 cd 都是他的姐哎,两点确定 一条直线,所以过这两个点的直线就是三 x 加二 y 等于一啦!你看点在员外,用带一半的方法就可以求出切点咸方程, 也就是说这个员外一点五七。他的缺点,弦方程就是代一棒得五减二乘 x 减二加上七加一乘外加一等于十,妥妥的! ok, 总结一下,如果点在圆上,把点坐标这么带一半就是切线方程,而点在圆外,这么带一半就是切点弦方程啦!好了,为师这就讲完了,徒儿们速速刷题去吧!
440绍兴教数学的王老师 02:30查看AI文稿AI文稿
02:30查看AI文稿AI文稿坟掘摆着了,你就说要不要吧?主包高中数学考了三年的一百四十,这个技巧用了三年半,可以说是真正的坟掘,但我发现很多高中老师都没有讲过,今天就分享给大家, 今天呢,我们要讲的就是如何来计算切线和切点弦的方程,尤其是在这个解析几何里,对吧?像圆啊,椭圆、双曲线和抛物线,这四种是最常见的,对吧?那我们拿椭圆来举个例子,这个坟掘的核心要点呢,就是交换, 比如说像第一个求切线,在这个椭圆上有一点 p, x 零外零,然后做了一条切线,现在呢,我想要求这个 切线 l 的 方程,对吧?那交换是什么呢?就是保持下面的常数不变,在上面 里面的一个 x, 因为它是个平方,对吧?把里面的一个 x 换成这个 x 零,就是 x 乘 x 零加上 y 也换掉,对吧?就是 y 乘以 y 零等于一,那么这个 我们现在发现它已经变成了一条直线的方程了,对吧?那么它就是这个切线 l 的 方程,切线 l 的 方程,那么对于这个切点弦方程呢?它是一模一样的啊, 和这个是一模一样的,只是条件换了,对吧?这个是从椭圆外一点 p, x 零外零,向这个椭圆引了两条切线,这个切点弦就是 ab, 我 们现在要算的是 ab 的 方程,所以说 ab 的 方程呢,也是这个东西, 明白吗?只是 p 点的位置不同,但是得到的结果永远是相同的。那么我们看下面这几种,像圆里面,我们怎么来换呢?那它对应的就是 x 减 a, 因为换掉一个,对吧?那就是 x 零减 a 加上 y 减 b 乘以 y 零减 b 就是 把里面的一个 x 一个 y 换掉就可以了,保持其他的常数不变,对吧?然后那这个双曲线呢?那和那个椭圆是不是几乎没什么区别啊? a 方分之 x 零, x 加比方 分之 y 零, y 等于一,这里是减号啊。 那么这个抛物线呢?它是什么呢?就是 y 乘以 y 零等于屁倍的 x 加 x 零,对吧?不管是切线还是切点弦啊,它们得到的方程都是一样的啊。好了,重点就是一个交换嘛,两个字啊。
192药师 03:08查看AI文稿AI文稿
03:08查看AI文稿AI文稿这个视频咱来讲讲切线方程。比如这个圆,圆心是圆点,半径是二,那圆方程显然是 x 方加外方等于四。如果在圆上选个点,一根号三吧。那我问你,过这个点且与圆相切的切线方程是啥? 这简单连接圆心和切点,这个点是一根号三,那他的斜率就是根号三。这两条线肯定垂直,斜率乘积复一, 那这条线的斜率就是负的三分之。根号三位有了斜率,又有个点,直接用点斜式写出方程,整理一下就是 x 加根号三,万减四等于零。 你看用斜率和定点就可以计算切线方程,这是比较科学的算法。咱再来讲个不大科学的要求。这个圆过一根号三的切线方程,你只要 把圆方程中的一个 x 换成一,一个 y 换成根号三就可以了,你看跟咱算出来的一样,所以只要把 xy 各换一半,就能得到切线方程。类似的,这个圆或根号二,根号二的切线方程就是根号二 x 加根号二, y 等于四。 那么问题来了,如果圆心不是圆点,比如这个圆过点一负四的切线方程怎么求呢? 嘿嘿,还是能用带一半的法子,把这个 x 换成一,把这个 y 换成负四,这个方程就是你要求的切线方程啦。 怎么样,带一半的方法好用吧?那么问题又来了,如果点在圆外,比如这个圆和这个点,那按照带一半的原则,这么写出来的直线方程还是切线吗? 当然不是,他是这个点向远影切线,这两个切点连线的直线方程,这叫切点斜方程。看着好像很有道理,可是为啥呢? 假设这个缺点是 ab, 根据切线方程,这条线就是 ax 加 by 等于一,类似的这个缺点是 cd, 那这条线就是 cx 加 dy 等于一, 这两条线的交点是三二,那三二就符合这个方程就有三 a 加二 d 等于一,而且又符合这个方程是三 c 加二 d 等于一。 仔细看看这俩柿子是不是可以理解为有一个方程叫三 x 加二 y 等于一,而 ab 和 cd 都是他的姐哎!两点确定一 条直线,所以过这两个点的直线就是三 x 加二 y 等于一啦!你看点在员外,用带一半的方法就可以求出切点咸方程, 也就是说这个员外一点五七,他的切点斜方程就是代一棒得五减二乘 x 减二加上七加一乘外加一等于十,妥妥的! ok, 总结一下,如果点在圆上,把点坐标这么带一半就是切线方程,而点在圆外,这么带一半就是切点弦方程啦!好了,为师这就讲完了,徒儿们速速刷题去吧!
2530在线学习高中部 02:01查看AI文稿AI文稿
02:01查看AI文稿AI文稿切点弦方程问题经常出现在咱们的选择题和填空题当中,那我怎么才能快速解决切点弦方程问题呢?哎,今天咱们一起来看一下。首先介绍一下什么是切点弦, 那就是过曲线外一个点,哎,做曲线的切线,切点是 a 和 b 的话, ab 之间的线段就是切点线,那在做题的时候经常去求切点线方程,哎,老师给大家一个口诀,平方便一次依次变平均,快速解决切点线方程。 现在咱们以这个原则曲线一般方程为例啊,给大家说一下, a, x 方加上 b, y 方加上 c, x 加 d, y 加 e 等于零。哎,那这里面呢,它有 x 方,有 y 方,那像这种平方的哎,我需要对它进行处理,变成 x 乘 x, y, y 的形式,而这个 x 和 y 依次的,哎,一次我要变成平均的,我先把它写成二分之 x 加 x, 二分之 y 加 y 的形式。 接下来呢,重点步骤来了,那我就要将许仙歪这一点的横纵坐标替换,这里面的其中一个矮子走过一个歪啊,那就变成这种形式,这个就是斜点斜方程对他进行画眼整理,就是咱们最终结果了。 那么平方面一次依次变平均,就可以解决圆椭圆双眼线抛线的前线方正问题,在这里面呢,哎,老师把咱这些内容都给大家进行整理了啊, 我再以椭圆这个方程为例,给大家进行详细再说一下,你看 x 方, my 方,初恋平方,我要写成 x 称 x, y 乘 y 的形式,然后将曲线外一点的横送坐标,哎,替换至您的其中一个 x 和一个 y, 得到切电线方程,所以平方便一次依次变平均解决原始曲线的切电线方程问题,你学会了吗?
303fairy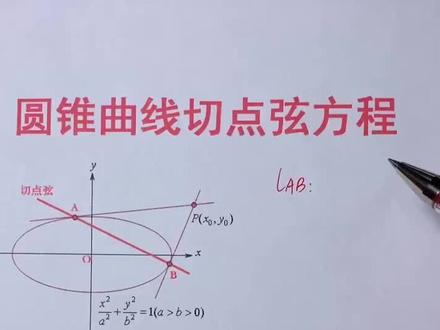 00:59查看AI文稿AI文稿
00:59查看AI文稿AI文稿同学们好,今天我们讲一下圆锥曲线的切点弦方程。首先我们来看椭圆,过椭圆外一点 px 零, y 零向椭圆做两条切线, 缺点分别是 ab, 然后我们把 ab 连起来,那么这条直线 ab 就是缺点弦,它的方程是可以直接被写出来的,而且方法非常简单,大家请看 ab 的方程就是把这里的 x 方改成 x 乘 x, 然后把这里的 y 方改成 y 成 y, 其他的都不动,然后把其中的一个 x y 分别用 x 零 y 零替代即可。 那如果是双曲线的话,同学们把这里的加号改成减号就可以了。那么同理,在抛物线中这条直线 ab, 他的方程就是把这里的 y 方改成 y 成 y, 把这里的二 px 改成 px 加 px, 然后把其中的一个 xy 用 x 零 y 零替代。
287永超简单数学 11:04查看AI文稿AI文稿
11:04查看AI文稿AI文稿你好,现在我们来推导一下圆锥曲线的切线方程。好,我们还是以椭圆为例子, 这个椭圆上面有一个点 p 好,这个时候切线,我们要要求它的 l 的方程好。第一种办法,我们先写出椭圆的标准方程, 我们对 x 求偏档 好,我们就可以得到 d y 变成 d, x 等于把这个移过去,然后再 把这个除过来。 好,这就是对 x 的偏导,我们现在只要把 p 点带入的话,这个就是它的弦律 k l 等于 好,椅子旋律,椅子这个点我们可以用点形式就可以把这个放 方程表示出来。啊,这是第一种方法,我们用偏导的方法来做。好,我们再讲第二种方法,使用极限的观点。 同样的我们还是画一个椭圆出来。 好,这里有点 p, p 点的指示, x 零, y 零。好,然后我在这里再取一点 q q 点的值,我设为 x 和 y。 好,我过 p q 这两点做这个椭圆的割线。 嗯,注意此时这个是割线,不,不是切线。 好,我现在这个 q 点不断地逼近这个 p 点,使这个割线变慢慢的变成它的切线。 好,我们来看一下会有什么。嗯,表达式好,首先我们选出图案的标准方程 好,因为我的 p 点和 q 点都在椭圆这个曲线 c e 上面。好,我们就有得到一组方程 好,这个唯一是这 为二十,这个一和二就是因为 p q 在曲线 c e 上面,我们把这个点带进来,满足这个方程,这个很容易理解好,然后我们再用一式减去二式好, 好,然后我们再把这,把这一项,把这一项移过去, 这里是一个完全平方,我们把它展开 好,然后我们把它, 把这一项,把它除过来,放在这里,把这把这一边,把它移过来。好,我们重新来写过。 好,我们现在这个 p 点不断的接近 q 点,不断的接近这个 p 点,我的 x 会不断的变,慢慢的变成 x 零, y 会不断的变成 y 零, 那么此时我直接可以把这个 x 和 y 的值直接带进去就可以了,因为它是它极限值。 好,我现在我可以把它画画成为 这个就是这条直线,这条勾线的弦域,此时这个 q 点是非常接近于 p 点的,所以 当 q 点完全和 p 点重合的时候,那这条勾线就变成了切线,那这个弦域就变成了在 p 点的弦域, 这个和我们刚才退了的结果是一样的。好,我们用点斜式把这个方程表示出来, 这就是我们要求的切线的方, 这些都是等价的两种不同的推导方法。另外第三种呢, 就是把这个直线把它设为 y, 等于 m x, 加上 b 和这个曲线 c e 盈利方程,然后使用这个第二条等于零,当它的只有一个根的时候,可以算出这个 m c b, 嗯, 求出 k k 的值,这个方法因为很很常用,我就这里不重复的退稿了。这就是我们 求椭圆切线的公式。好,我们现在来推导一下,如果说 这个点 p 点不在椭圆上,我们由这个 p 点引两条切线,我们求这两个切点之间的 直线方程,求这个 l, 求我这个蓝色这个线的直线方程怎么求?好, 同样的,我们先把这个图把它移过来。 好,此时我的 p 点在这个椭圆 y, 我不反射,这个点为 m, 这个点为 n, 其中 m 的坐标我把它写为 m 和 n, n 的坐标,我把它写为 c 和 d。 根据我们刚刚推导的切线的方程, 我们现在只需要把 m 点和 m 点带进这个切点方程,就可以得到它们的切线方程。 好,第一条切线,我把它设为,嗯, l 一,这个是 m 点的切线, m 点的切线设为 l 二,那 l 一是等于 and r 的期限式内容。 这个方程有什么像素? 我们可以得到点 p, 它既在 l 一上,也在 l 二上。因为点 p 是这两个线的焦点,这个 p 点是焦点,所以点 p 是肯定会满足 l 一的方程,同样的也会满足 l 二的方程。 这两个直线方程。好,我们现在 把这个 m 的横坐标和 m 的横坐标 c, 把它换成 x, 把 n 和 d 这个重坐标我们换成 y, 我们把这两个边量带到这两个等式里面去,我们会得到一个新的方程。 因为如果一条直线的方程有两,有两个点满足这个直线的方程,那么就可以说这个方程 是这个曲线的方程,这个直线是这个方程的曲线。 很明显, m 点和 n 点都满足这个方程,所以过 m 和 n 的直线就是这个方程。
35婷姐聊教育 02:16查看AI文稿AI文稿
02:16查看AI文稿AI文稿圆的切线方程和切点线方程又是一个可以值得探讨的知识点,那么如何来快速学习它?同学们跟着刘老师的脚步走起来。哈喽,各位同学,我是数学刘老师,那么今天呢,给大家分享的这个切线方程和切点线方程是什么呢?先上结论 啊,怎么来说呢?就是说已经知道了圆上的一个点,然后过这个点的切线方程是多少,同时呢,在圆外有一个点,通过这个点的作圆的两条切线,他分别交源于 ab 两点,那么 ab 这条直线的表达是等于多少呢?好,来同学们解惑一下。 好,怎么来理解呢?用一句话来说,叫去一个留一个就 ok 了。比如说 a k 十减 a 的 平方,你就可以把它写成 a k 十减 a 来乘以 a k 十零减 a。 好, y 减 b 的 平方,你可以写成 y 减 b 来乘以 y 零减 b。 ok, 就 结束了。好,来,我们来看看题吧。好来,比如说这个题过点二到二做圆的切线, 那这切线方程是多少?那我怎么办?去一个留一个。同学们来看啊,那写成 a k 减一,乘以 a k 是 零减一,加上 y 减一来乘以 y 零减一,是不是等于二?那么这个 a k 零和 y 零就二得二,那结果就等于 a k 减一 来乘以多少二减一等于一,加上 y 减一来乘以多少一,是不是等于二啊?那画完减就是 a k 十减一,加上 y 减一等于二,就能得到 a k 四加 y 减四等于零。好了,我们的切线方程就出来了,同学们有没有十秒钟?那如果说你不知道这个切线方程,你看看这个点如何写 好,那下面这个题也是一样的,那我一样的可以是干嘛?老师也是去一个,那就是 a k 减一乘以 a k 是 零减一,加上 y 减二来乘以 y 零减二是不是等于四啊? 那么就得到多少? a x 减一来乘以一,加上 y 减二来乘以三,是不是等于四?换完结果就是 a x 减一加上三, y 减六是不是等于四啊?最后就得到 a x 加三, y 减十一就等于零了。 好来,同学们明白了,如果说你不知道他的牵线方式和牵连线方式,那么这两个题你可以把它写上,它就是一个难题了。但如果说你知道了他,那么同学们记着两个字啊,叫秒杀,那么就很容易就能出来。 ok, 那 么这一次给大家分享就到这里了,我们下期再见吧,拜拜。
 17:38查看AI文稿AI文稿
17:38查看AI文稿AI文稿同学们好,我们今天来看到切线与切点方程,这个呢,切线与切点方程我之前提到过很多次,我相信同学们也应该能记住。我们今天主要是来讲一下他怎么利用同构的思想来证明他,你说我们在考试的时候该怎么书写他,我们来回忆一下, 以及我们的抛物线,椭圆双曲线,我们体用的就是什么大一半的思想吗?比如我们看到椭圆 a 方分之 x 方加 b 方分之 y 方等于一, 如果呢,这个点它在我们的曲线上面,我们直接求出来了,我们令 x 方变成 x 零倍的 x, y 方呢?变成 y 零 y, 这个 x 零 y 零就是我们怎么样在曲线上的那个点,那么此时我们写出来的就是它的切线方程。 如果曲线 y 一个点 d, 我 们即为 x 一 y 一, 我们同样采用大一半的思想,那么此时呢,我们写出来的呃,这个直线方程它就不再是切线方程了,它就是我们的切点弦方程。什么叫切点弦方程,相信同学们应该也能理解, 比如我们以圆举例,好,我们这里有个圆,圆外面有一点,我们过这个点做圆的两条切线,那么切线呢?它会与圆有两条,对不对? 我们这两条切线的切点相相连起来。好假设这个弦它为 ab, 那 么此时呢,我们方程写出来就是我们的 ab 这条直线的方程啊,当然这里我们圆没有写出来啊, 椭圆也是一样的写出来的呢,如果这个圆换成椭圆,那么我们 ab 的 直线方程就是它。下面我们来证明一下,我们来看到圆吧,圆我们是去怎么证明的呢?首先我们来看到这个点,它在圆上啊,我们设点 p, 它为 x 零, y 零圆的方程呢? x 减 a 方加上 y 减 b 方等于 r 方,我们圆心为 ab。 从这个呃相切的时候,我们是知道我们这条 o p 直线,因为它两个点都知道吗?所以我们 o p 的 斜率是能求出来,我们先把 o p 的 斜率写出来啊,我们 k o p, 你 利用两个点是能求出来的,我们的 y 零减去 b 比上一个我们的 x 零减去 a。 我 们既然 o p 这条直线的斜率求出来,因为它切线与直径的斜率是不是也能写出来?我们切线的斜率?我们写一下 k 切线的斜率,它应该呢就等于负的,我们的 x 零减 a 比上 y 零减 b, 因为我们两直线如果垂直,我们的斜率相乘呢? k 一 乘以 k 二等于负一,对不对?好,我们现在直线的斜率也写出来了,说我们现在是不是能够把直线它的方程给写出来?你有斜率有一个点, 专门根据点斜式,我们把直线的方程给写出来,我们把切线方程给写出来。切线方程呢,就是我们的 y 减去 y 零, 我们刚刚求的切线的斜率,负的 y 零减 b, 分 之 x 零减 a。 还有呢就是我们的 x 减去 x 零。好,我们稍微整理一下,我们通过这个式子我们去整理,我们能得到我们把分母截乘过来, y 减 y 零乘以一个我们的 y 零减去 b 等于负的括号 x 零减 a, 再乘以 x 减去 x 零,我们把它展开就能得到我们的 y 乘以 y 零减去 y 乘以 b, 再减去我们的 y 零方,然后呢再加上 y 零 b, 对 不对?我们右边同样去展开,等于负的 x 零 x, 再加上我们的 x 零方,然后呢?加上 a 倍的 x, 再减去 a 倍的 x 零,我们把这个式子稍微化解一下, 我们把我们的 x 零方啊,以及 y 零方, x 零方啊, y 零方,一切是零, x 零方,还有呢,我们关于我们的 y 零以及 x 零放到一边去,为什么?因为我们知道,我们现在知道它的结论嘛,是不是?是一个关于 x 零以及 y 零放到一边嘛?对不对?我们把它放到旁边去,放到一起 我们就能得到我们的。呃,我们整理一下,我们先把 x 零方拿过来,就是我们的 x 零方,然后呢再加上一个 y 零方,我们系数都写成正的好了,然后减去我们 a 倍的 x 零,然后呢?减去 b 倍的 y 零, 等于我们的 x 零 x, 再加上 y 零 y 啊,然后呢?再减去我们的 a x, 减去 b y, 我 们为什么会这样写呢?因为我们的切点 x 零 y 零,它是在圆上,所以可以把这个点带到圆里面去我们的圆啊,带进去之后,你就会得到这样一个方程, x 零减去 a 的 平方,然后加上 y 零,减去 b 的 平方,等于 r 方,对不对?我们把这个式子展开,就能得到 x 零方,加上 a 方,然后减去两倍的 a x 零,然后我们写到下面啊,加上 y 零方, 然后加上我们的 b 方,再减去两倍的 b y 零,等于我们的 r 方,所以呢,我们想的是我们把 x 零方以及 y 零方放到一起,然后呢,通过一些配凑的思想,可以把这一步啊简化一下。简化成什么?简化成我们的 r 方嘛?我最希望是这样,对不对?因为你最后面有一个 r 方嘛,所以我们把它简化成 r 方的时候, 这里跟它来比是不是差了一些像素?所以我们呢,需要去配凑一下我们这个式子,以及跟这个式子来对比一下。首先我们差了一个 a 方,还有什么 b 方,对不对?还差了一个负的 a x 零,以及一个负的 b y 零,所以我们把左边加上一些我们的差的像素,它就变成了什么?变成了我们的 r 方, 你左边加了,你右边自然得加吧。右边我们原本是有 x 零 x 加上 y 零 y, 然后减去 a x, 减去 b y, 把我们刚刚左边凑的那些项数加上。好,它是凑哪些项?所以我们凑了一个 a 方,然后呢?一个 负的 a x 零,然后一个 b 方,然后一个负的 b y 零,我们刚刚是凑了这些项数吧,所以我们左边现在变成了 r 方,然后右边这里我们去整理一下。怎么整理啊? 我们把我们的呀,哎啊 a 放到一起,以及呢?我们的 b 放到一起,我们就会得到一个等于啊,我们写的左边是 r 方,对不对?我们变成了 a 方,减去括号 x, 加上 x 零倍的 a, 然后呢?再加上 你有一个什么?有一个我们的 y 零 y, 还有一个我们的 x 零 x 吧,这两个我们哪个跟它放在一起啊?肯定是 x 零 x 嘛,因为我们这边只有 x 零与 x, 对 不对?所以呢,再加上一个我们的 x 零 x, 然后同样我们把 b 也放到一起,加上一个 b 方,减去括号,我们的 y 加上 y 零倍的, 然后再加上 y y 零,那么观察这个设置,它是不是可以通过十字相乘,可以把它音式分解,所以呢,最后我们就能得到我们的 r 方,它等于我们的 a 减 x 零乘以一个我们的 a 减 x, 然后加上 b 减 y 零乘以一个我们的 b 减 y。 好, 我们把这个括号里面同乘一个负一,所以呢,我们可以把它变成我们需要的这种形式, r 方就等于 x 零减 a, 然后乘以 x 减 a, 然后呢再加上 y 零减 b 啊,减 b, 不好意思, 再乘以一个 y 减 b。 所以呢,这里我们圆的切线方程是不是就根据我们的这些性质啊,条件以及东西,我们推导出来了,对不对? 当然我们考试的时候这些计算步骤啊,从这里一直到这里,我们都是不需要去写的,我们要写的是什么呀?我们首先把它的斜率写出来,然后呢把我们的切线写出来,对不对?然后你这里只要到这里为止,你只要写一个什么,我们的整理啊,整理得怎么整理的呢?老师是不会去管你的, 整理得我们直接得到什么,得到我们最后的结论就可以了。所以我们的切点弦方程啊,这个叫切线方程,不好意思,我们的切线方程呢,就可以通过我们的书写把它表达出来,我们接着再来推导一下我们圆上的切点弦方程,此时我们的 p 点 x 零, y 零呢,它在圆外,它不在圆上了, 好过这个点我们是可以做两条圆的切线,对不对?第一个切点我们记为 a 点为 x 一 y 二, 我们经过我们刚刚推了,我们是能通过 a 点直接把 pa 这条切线给写出来吧。因为 a 点 x y 呢,它是在圆上, 所以我们 pa 这条直线,我们是可以直接写出来的。 pa 呢?它就是我们的 x 一 减去 a, 然后乘以我们的 x 减 a, 然后加上 y 一 减去 b, 乘以一个我们的 y 减去 b, 等于 r 方,对不对?同样呢, p b 我 们也是可以写出来, p b 就是 我们的 x 二减去 a, 乘以一个我们的 x 减 a, 然后加上一个我们的 y 二减 b, 乘以一个我们的 y 减 b。 好, 现在我们的 pa 以及 pa 这两条直线我们都写出来,对不对?我们现在要求的什么?求的是 ab 这条直线的方程吧。这两条直线呢,有一个什么规律?看到我们的 p 点,它既在我们的 pa 上,也在我们的 p b 上,所以呢,我们把 p 点去带入这两条直线,我们将我们的 p 带入直线,我们带入直线可以得到什么样两个方程,对不对?我们能得到第一个,我们带入 pa, 能得到我们的 x 一 减去 a, 乘以一个我们的 x 零减 a。 其实我们的 x 变成了什么?变成了我们 p 点的横坐标嘛? 加上我们的 y 一 啊, y 零减 b, 再乘以一个我们的 y 一 减去 b, 等于 r 方,没问题吧? 然后呢,同样我们还在第二条直线 p b 上面说明,能得到我们的 x 二减去 a 乘一个我们的 x 零减去 a, 再加上一个我们的 y 零减去 b, 乘一个什么?我们的 y 二减去 b 等于 r 方。根据我们之前讲的通购的思想,我们会发现一个问题, 这两个式子除了我们的 y 一 y 二以及 x 一 x 二 x 二不一样,其他的呢,都是一样的,对不对?所以呢,我们就可以说我们的 ab 两个点它都满足我们的直线,我们的 x 减去 a 乘一个,我们的 x 零减去 a, 再加上一个,我们的 y 零减去 b 乘以一个什么?我们的 y 减 b 等于 r 方,我们的 a 点以及 b 点是不是都满足这个式子?所以呢,这条直线就是我们的什么切点前方程啊,这就是它的推导过程,相信同学们能够理解。这里呢,我们是不是就用到了我们所讲的什么同构的思想对不对? 我们利用了同根的思想证明了我们圆的切线方程以及切点弦的方程,那么在椭圆里面,其实我们的也是一样的,对不对?下面我们来证明一下椭圆它的切线以及切点弦方程是怎么推导过来的。先来证明我们的 p 点在椭圆上, p 点为 x 零, y 零 或 p 点做椭圆的切线。我们知道这条切线方程呢,我们根据我们前面的结论是可以直接写出来,对不对?我们的 a 方分之 y 零乘以 y 等于一,好,下面我们来推导。 首先呢,这里有一个问题,我们这条直线的斜率 k 啊,它不再是圆了吧,它不能说与圆心啊,与斜点相连是垂直,它没有这个性质对不对?那我们只能怎么样?我们根据我们这条直线,然后呢与椭圆去连立,我们得它等于零来把 k 求出来,对不对?所以我们第一种方法好,我们这个直线呢, p 啊,这条切线,我们知道 p 点是 x 零 y, 我 们设它的斜率为 k, 当然这前提是我们的 k 存在嘛,所以 y 等于我们的 k 倍的括号 x 减去 x 零,我们把右边的减 y 零啊,左边减 y 零,直接拿到右边来,那根据我们的椭圆连力, a 方分之 x 方加上 b 方分之 y 方等于一, 我们呢,这里直接就算一下我们的德塔,我们德塔是不是等于零?两个直线啊,曲线与曲线与直线相切,我们的德塔是等于零,那么德塔我们可以用我们之前讲到的应解定律写出来,它应该只有等于我们的 a 方 k 方 加上 b 方减去啊,加上 b 方减去我们的括号负 k x 零,再加上 y 零括号的平方,它是不是等于零? 我们当然可以利用这个得它等于零去求出我们的什么我们的斜率 k, 但这个问题,它的计算量呢?是不是挺大的?计算量大,所以呢,我们 不推荐用这个方法啊,去求助这个 k, 那 我们 k 还该怎么办?我们有第二种方法啊,第二种方法呢?当然没有学到求导的同学,没有学到导数的同学可能是听不太明白了,我们可以通过去求导,求导之后我们的什么,我们的 y 一 撇,是不是就是等于我们的 k 啊?没问题吧, 但是这里的对于 y 求导,我们是什么呀?我们的 y, 它是椭圆方程里面的 y 吧。好,这里涉及到我们的引函数求导,如果大家不会的话,那也没办法,我们大概这里稍微提一下, 我们对它来求导。首先呢,我们 a 方分支对 x 求导就变成了什么, x 方就变成了二 x, 对 不对?然后加上我们的 b 方分支,我们 y 方求导呢?首先我们对 y 方求导就是二 y, 但是这里要注意,同学们,这里的 y 是 什么呀?它是一个关于 x 的 方程,我们可以把这个 y 解出来吗?它是根号多少多少,对不对? 所以呢,我们对 y 求导之后, y 呢,它是一个复合函数,所以我们还要对 y 再求一次导,就是 y 一 撇好,右边呢,也求导,一求导就是零,对不对?所以我们可以根据这个求导的公式,我们可以把我们的 y 一 撇给求出来吧, y 一 撇呢,它求出来就等于负的 a 方分之 b 方,然后呢,再乘一个我们的 y 分 之 x, 此时呢,他让我们求的是什么?是 x 零 x 零以及 y 零处的切线的斜率,对不对?所以呢,我们这里就能求出来我们的切线的斜率啊,他只要把我们的 x 零 y 带进去,就能变成我们的负的 a 方 y 零分之 b 方 x 零。所以呢,此时我们的切线的斜率又求出来了吧,如果同学们能够理解这种方法是很快的,如果真的理解不了,你还只能去老老实实的连力把我们的 k 呢,能求出来, 考试的时候怎么办?我们先连力把得到写出来,然后呢,通过自己去在草稿纸上去求导之后我们把 y 一 撇啊给求出来,然后直接把斜率我们写到这里就可以了,老师是不会去管你的计算过程的。所以呢,此时我们的切线的直线方程是不是可以写出来?我们切线我们现在点也知道了,斜率也知道了,我们把它写出来就是 y 减去 y 零, 等于我们的 k 就是 负的,我们的 a 方分之 y 零,分之 b 方分之 x 零,对不对?这就是我们的 k 嘛,然后再乘以我们的 x 减去 x 零。好,我们整理一下,就能变成我们的 b 方 x 零 x, 再加上我们的 a 方 y 零 y 等于我们的 a 方 y 零方, 再加上一个我们的什么 b 方 x 零方,然后呢?这个式子怎么办?我们要的是什么?我们知道结论对不对?我们他要的是分式嘛?所以我这个式子每一项都就除以一个我们的 a 方 b 方, 我们整个式子除以 a 方 b 方,它就变成了什么?其实我们的第一项,你除以 a 方 b 方 a 方 b 方 b 方,是不是约掉了?所以变成了我们的 a 方分之 x 零 x, 加上我们的什么 b 方分之 y 零 y, 然后呢,就等于我们的 b 方分之 y 零方,再加上 a 方分之 x 零方,这个是什么呀?我们把这个 p 点带到我们的椭圆里,是不是成立的?我们 p 点带进去就能得到我们的 a 方分之 x 零方,然后加上 b 方分之 y 零方,等于一,对不对?所以这一项它其实就是一嘛?然后呢,我们把它写出来等于一,所以最后我们就等得到这个我们的切线啊,斜切线的方程对不对?它是我们的 a 方分之 x 零,乘以 x, 加上我们的 b 方分之 y 零 y 等于一,就求完了。接下来我们再看一下,我们的 p 点在椭圆外,此时我们的 b 方分之 y 零 y 等于一,就求完了。接下来我们的什么切点弦方程? 我们这个切点弦方程,首先我们结论,我们是知道对不对?它是我们的 a 方分之 x, 零乘以 x 加上我们的 b 方分之 y, 零 y 等于一嘛,那我们怎么求呢? 首先我们得把我们的 pa 或者说 pb 它的斜率给求出来吧,那我们求斜率有几种方法?刚刚前面讲的话,第一种我们连力好,连力之后怎么样?我们知道得它,它是等于零的,是能求出 k 的 斜率,对不对?切线的斜率。第二种方法呢,就是我们的求导,求导同学们如果用的不熟练,或者说我们的 高二的同学们没有讲到导数的这一块的时候,我们可以参考一下这里。但是我们考试的时候,你这个求导的方法他是不能直接写上去的,你可以在草稿纸上把求导的过程,求导的方法 不能写上去,我们在草稿纸上求导,把 k 切线求出来,然后呢,写到前面去,我们简写下就可以了。所以呢,这个方法他也是可以求助我们的切线的斜率,并且呢,他的计算量是很少的,对不对?所以通过我们这里,他能够把我们的切线的方程给求出来吧。 好,那我们前面写过,我们这里就简写一下我们的 p a 这条直线方程,我们是 a 方分之 x 乘以 x, 加上 b 方分之 y 乘以 y, 等于一,对不对?然后呢,我们的 p b 这条直线呢,就是我们的 a 方分之 x 啊,不好意思,这里不是 x 零了,这里是 x 一, 对不对?因为我们的切点呢, a 它是 x 一 y 一, 我们的 p b 它是 x 二,乘以 x, 加上我们的 b 方分之 y 乘以 y 等于一。 所以呢,我们 p a 以及 p b 的 直线都写出来了吧?我们知道我们的 p 点它既在 p a 上又在哪里?又在 p b 上,所以我们把 p 点带入到这两个方程。好,我们看看能得到什么?我们将 p 带入, 将啊,将我们的 p 点带入,带入之后呢,我们能得到两个设置,第一个,我们带到 p a 里面去,就变成了我们的 a 方分之 x 一 乘以我们 x 零,再加上 b 方分之 y 一 乘以 y 零,等于。带到我们 p b 点去呢,就变成了 a 方分之 x 二乘以 x 零,再加上 b 方分之 y 二乘以 y 零,等于,对不对?我们用前面的同口思想,我们知道这里除了 x 一 x 二, y 一 y 二不一样,其他都是一样的吧。所以我们可以说我们的 p 点它在哪里?在我们的直线哪里啊? 呃,不对,是我们的 ab 两个点啊,不好意思,这里是我们的 x 一 x 二不一样,说我们 ab 两个点,它是在直线哪里?在我们的直线,我们的 a 方分之 x 零乘以我们的 x, 加上 b 方分之 y 乘以 y, 等于一这条直线里面吧。我们的 ab 它是在这条直线,所以我们的 ab 直线呢,就能够写出来 说我们 ab 它最后的直线就是我们这个。这里我们利用到了什么?也说我们前面讲的通勾的思想,就把椭圆我们的切点方啊,切点弦方程给证明出来了。双曲线以及抛线的证明过程呢,也是一样的,特别是我们的椭圆里面啊, 我们如果要去求大体里面出现了,我们求怎么办?我们首先去连力把得它给写出来,你用因解定力也是可以的啊,通过求导我们把我们的 k 去求出来之后带入前面就可以了,因为我们前面这个方法计算量实在是有点大, 好,出来之后呢,我们就能把切线给求出来,对不对?那今天这节课呢,我相信同学们应该能够理解,比较简单。好,那么今天讲这里感谢我们收听,再见。
45杨杨杨讲数学 17:19查看AI文稿AI文稿
17:19查看AI文稿AI文稿在圆锥曲线中,有这样一类基本问题,比如圆字圆外一点向圆引两条切线,求过两个切点的直线方程。 再比如抛物线四,抛物线外一点向抛物线引两条切线, 连接两个切点的线段呢?我们叫做切点弦,求切点弦所在直线方程。 这一类问题,我们先从原开始 已有结论。我们知道过圆上一点 p, 它的切线方程是在圆的方程的基础上,把 x 方写成 x 零, x 把外方写成外零外,于是这就是过圆上一点 p 的切线方程。在此基础上,我们研究 从圆外一点劈向圆引两条切线,过这两个切点的直线方程, 设 a、 b 两点的坐标, 那么过 a 的切线方程,当然利用已知结论把参数带进去,得到方程一。 过 b 点的切线方程,把 b 的参数带到已知结论中,得到方程二。 由于 p 点在第一条切线上,那么 p 点坐标就满足方程一。代入以后呢,得到方程三, 同样 p 在第二条切线上,那么把 p 的坐标带入到方程 乘二,得到等十四,观察等十三和等十四,他们的唯二不同是 x、 e、 x 二以及 y 一、 y 二, 我们把这个不同分别用 x 和 y 来表示。得到了方程五, 那么 a 点显然满足方程, 因为你把 a 带到方程五,那就是等于三嘛。同样 b 也满足方程五。 观察方程五的特点, x 和 和 x 零是乘的关系,我们可以利用乘法的交换率把它调一个序,同样 y 和 y 零也可以调一个序,于是方程五他当然就是方程六。 那么 a、 b 两点满足方程六。方程六本身呢?又是关于 x y 的二元一次方程,它是一条直线,又过这两个点,当然它就是直线 a b 的方程, 也就是过这两个千点 a b 的所求的直线方程。 好,结论出来, 答案呢,是它。我们注意到这个答案方程六与已知的这个结论过原上一点 p 的切线方程,形式上是完全一致的。 哎,这个结论有没有推广的可能性呢?我们研究一下椭圆, 同样已知结论,过椭圆上一点 p, 它的切线方程将 x 方写成 x 零 x y 方写成 y 零 y。 啊,这咱们以前讲过,是这样的一个直线方程。 接下来还是设两个切点为 a b, 那么过 a 的切线方程,把 a 的坐标带入到这个已知结论中,得到方程一。 过点 be 的切,写方程,把 be 的坐标带入到已知结论,得到方程二。 由于点 p 在第一条切线上,那么点 p 的坐标当然满足方程一啊,带入以后得到等式三。 点 p 在第二条切线上啊,点 p 的坐标带入方程二,得到等于十四。 对于等式三和等式 四而言,它们的 v 二不同,是 x 一 x 二以及 y 一 y 二,把这两个位置用 x 和 y 来表示,就得到了方程五。 根据等式三和四,那他就说明 a 点坐标和 b 点坐标满足方程。 同样方程五中 x 零 x 以及 y y 零, 那么它都是乘之间的关系,利用乘法交换率换一个顺序, a b 也在这条方程所表示的直线上。 好,这条直线呢?啊,是关于 x by 的二元一次方程,是一条直线,它又过 a b, 那么方程六就是直线 a b 的方程,而且方程六在形式上与过椭圆上一点 p 的线方程是一致的。 哎,我们发现圆和椭圆都有这样同样的结论, 过两个切点,也就是切点弦所在的直线方程,与我们曾经的过圆锥曲线上一点的切线方程是一致的。 那么对于抛物线,对于双曲线,对于圆心不在圆点的圆,是不是也有 同样的结论呢? 现在我们先复习一下已有知识。过圆锥曲线上一点的切线,对于圆而言,它的切线 对于一个一般式方程的圆,它的切写,注意这里呢,是把 x 方写成 x n x y 方写成 y 零, y x 是写成二分之 x x 零, y 是写成二分之 y 加 y 零。 椭圆双曲线抛物线,抛物线呢,外方是它这个二和 x 合在一起替换 成 x x 里 好。那么以上呢,我们把圆锥曲线过其上一点的切线,通过代换的方式就能够得到相应的切线方程。 那我们的猜想呢,就是从圆锥曲线外一点向圆锥曲线引两条切线,这个切点弦所在之间方程与过切点的切线方程形式上一致。 既然有这样的一个猜想,我们对于这个一般性的问题,能不能进行统一证明? 好,同样已知结论,刚才呢,有这么多条,我们把它做一个抽象概括, 过圆锥曲线 c 上一点的切线呢,我们给它设成一个这样的方程,以 x y 为变量,以这个 x 零 y 零为参数的这样的一个二元一次方程 好,还是熟悉的配方,还是熟悉的味道,设圆锥曲线啊,这里不一定是个圆了 的两点 a b, 那么以 a 为切点的切线当然是方程一,以 b 为切点的切线当然是方程二, 由于 p 呢,在第一条线线上,那么 p 点坐标满足方程一,所以把 p 点的坐标带入到方程一,得到等式三, 这里是 x 零 y 零。同样啊, p 点在第二条切线上,那么 p 点坐标满足方程二,带路得到等式死。 同样,对于等式三和等式四而言,它们的唯二不同是,这里 x, c, x 以及 y 一 y 二, 把它们用 x y 来表示,就得到了方程五,那么 a a 点坐标, b 点坐标当然满足方程 哎,注意到,方程五和刚才这个已对结论并不一样,因为他们的参数和变量的顺序不同。 观察一下方程五,我们再回顾一下刚才,那么这些就是刚才这个 f x y x 零 y 零, 那么这些方程它具有一个特征,就是 x 和 x 零之间或者是乘的关系,或者是加的关系,按照加法的交换率和乘法的交换率,我们可以把它换 一个顺序。同样, y 和 y 也是乘的关系,或者是加的关系,他们是对称的,可以换序。 所以对于方程五而言,我们可以把 x 零和 x 换一个顺序, y 零和 y 换一个顺序,也就是说,我们可以给它改写为方程六。 好了,方程六呢,首先,刚才我们知道它是一个二元一次方程,它表示一条直线,其次呢,它又过 a b 这两点,那么方程六就是直线, a b 的方程就是过两个切点的直线方程,而 而且你看,方程六与这个方程是一致的。 好,到此为止呢,我们就得到了这个一般性问题的结论,过远锥曲线外一点啊,引两条切线,那么过两个切点直线方程,它在形式上与过切点的切线方程完全一致。 我们把刚才证明过程的核心再重复一遍, 过 a 的切线方程一,过 b 的切线方程二, p 点,再切线一和二上,那么 切点带入以后,得到等式三和等式四,把它们的为二不同,用 x y 替代,得到了方程。 方程五本身的特性。我们知道 x 零和 x 是对称的, y 零和 y 是对称的,所以呢,作为一个对称变换,就得到了方程六。 方程六呢,是一条直线,又过 a b, 那么就是所求,而且方程六与一致的这个结论是一致的。 好,请你体会这其中的方程思想。好了,对于这个一般性问题, 我们有一般性的结论,那么对于抛物线,对于双曲线也有同样的结论,我们得到这一类问题的所有的结论都是一样的,它就是以前的过切点的切线方程, 我们可以拿抛物线再做一个验证。这个证明过程啊,还是熟悉的套路,设切点 a b, 过 a 的切线当然是它,过 b 的切线,当然是方程二 点 p, 在 p a 和 p b 上,把 p 点坐标带入方程一和方程二,得到等式三和等式四。 对于这两个等式,把其中的变化 y x 得到了方程五, 那么方程五呢? y 零 y 是对称的,利用乘法交换率, x 零 x 是加法交换率, 那么方程六是一条直线,有过 a b, 那它就是所求,而且方程六与已知的这个过切点的切线是一致的, 那也就是说,我们有过切点的切写方程,我们直接就得到了切点弦所在直线方程啊,照着抄就可以。 好,我们做一个总结,两类问题,切点弦走在之前方程,切线方程,他们是 在我们的数学的学习中,一个关键能力就是抽象概括的能力, 要善于发现相关问题的共性。我们从一开始的圆和椭圆中得到了一个结论,就是切点弦所在之间方程与切线方程一致, 那么我们由特殊到一般,提出一个一般性的问题,然后我们加以证明,由此呢,我们就得到了这样的一个一般性的结论, 那么所有问题就迎刃而解不在话下。抛物线呀,双曲线呀,圆心不在圆点的圆啊,不过就是个渣渣, 直接逃用。当牛顿抽象概括出牛一、牛二、牛三,整个经典力学就此全面打开。 人类智慧的进步,本质上就是从不断的抽象概括中一步步走来, 按照惯例,学以致用。小试牛刀,答案在评论区 最后点个赞,看着我头像没?系列专题倍香!
 05:09查看AI文稿AI文稿
05:09查看AI文稿AI文稿大家好,今天我们来看一个圆的切点弦方程的球法。线弦则是过圆外一点做椅子圆的两条切线,两个切点的连线叫做切点弦, 如图,点 p 是圆 c 外的一个点,过点 p 做圆 c 的两条切线 p a, pb。 缺点呢是 ab, ab 这个线段叫做切点弦。 那如何去求这个切点线所在的直线方程呢?我们来推导一下,假设这个圆 c, 他的方程是 x 减 a 的平方,再加上 y 减 b 的平方,等于二的平方。点 p 是圆 c 外一个点 坐标是 x 零,逗号万林。接下来我们来去求这个切点弦 ab 的直线方程。 因为 p a 和 pb 是原 c 的两条切线,所以呢, c a 和 p a 是相互垂直的, cb 和 pb 也是相互垂直。所以呢,我们可以知道,那 c a、 p、 b 这四点应该共圆,他们都在以 pc 为直径的圆上,我们以 pc 为直径画出一个圆,这个圆呢,刚好经过 ab 两点,这样我们发现 ab 这两个点是以 pc 为直径的圆 和原 c 的公共点。这样我就可以把切点弦给他转化成两元相交的公共弦了。两元相交公共弦的方程比较好求,直接把两元的方程连立一相减就可以了。 所以呢,我们先去求以 pc 为直径的圆的方程。因为点 p 的坐标是 x, 零,逗号 b, 点 c 的坐标是 a, 逗号 b。 所以呢,以 pc 为直径的圆的方程,那就是 x 减 x, 零,再乘上 x 减 a, 再加上 y 减 y, 零乘上 y 减 b, 等于零,这样得到以 pc 为直径的 圆的方程。然后呢,元 c 的方程是已知的,我们将两个圆的方程连立,去求公共弦 ab 的方程, x 减 a 的平方,再加上 y 减 b 的平方,等于二的平方。 x 减 x 零, 再乘上 x 减 a, 再加上 y 减 y 零乘上 y 减 b 等于零。 把两四一相减,把 x 平方外放,销量一减二化减得就是 x 减 a, 再乘上 x 零减 a, 再加上 y 减 b, 乘上 y 零减 b 等于二的平方。 这样我们就可以得到公共弦 ab 的方程,也就是切点弦的方程的。有了这个公式以后,我们就很容易去求一个圆他的切点弦的方程, 这方程很好记,直接把元式的方程给他改写成 x 减 a, 再乘上 x 减 a, y 减 b。 方呢,给他写成 y 减 b, 再乘上 y 减 b 等于二的平方。然后呢,你直接把这个 x 是减 a 和 y 减 b 这两项中的 x y 换乘点 p 的横坐标和坐标,这样得到的方程就是切点弦的方程。点 p 负二多少一为圆 c i 减一的平方,加上 y 的平方等于四。 外的一个点过点批呢,做圆穗的两条切线切点呢,分别是 ab 两点,则求直线 ab 的方程,直线 ab 就是圆穗的切点弦。根据我们刚才欠弦的公式, 我们直接写就行了。把原式的方程给他改写成 x 减一,再乘上二减一,加上 y 乘 y 等于四, 然后点撇图标是分多少一。所以呢,直接带入,那就是 x 减一,再乘上,把 x 换成分负二减一,加上 y 乘上 y 呢,再给他换成一个一等于四。化解一下,那就是负三 x 加三加外等于四。这里的三 x 减外加一等于零。所以这个缺点弦 ab 的方程就是三 x 减外加一等于零。
565小牛高中数学 00:57查看AI文稿AI文稿
00:57查看AI文稿AI文稿你知道圆嘴曲线当中究竟哪一个题型近几年考的最多吗?哎,没错,缺点写问题。二零一九二零二零二零二一,连续三年考到老谢教你一招,写一半,留一半。抛物线 x 平方等于二 y 准现方程 ly 等于负的二分之一。 点 p 在嘴线上,可以假设 p 点坐标 t 负二分之一过点 p 引抛物线两条接线 papb, ab 为缺点,所以直接 ab 为缺点弦,其方程写一半留一半就是 t 乘以 x 等于一倍的 负二分之一,加上 y, 也就是 y 等于 tx 加上二分之一,所以直线 ab 的斜率 k 就等于 t, 而直线 ab 轻音协调三分之派,所以斜率 k 还等于摊挺的三分之派,等于根号三。因此 p 点横坐标 t 等于根号三。搞定,你学会了吗?
1.4万DZT老谢高中数学 20:48
20:48
猜你喜欢
最新视频
- 3289盼望





