今天咱们继续根据河北单招考试数学大纲来来梳理一下数学考试知识点。然后咱们看立体几何部分,我们认识柱、锥、台球的结构特征,并且要用公式来计算表面积和体积。那今天咱们就来梳理一下柱体,锥体、台体及球体是怎么求表面及体积的? 咱们先从柱体来看,柱体的侧面积呢?等于二 pi l, 那 柱体的表面积 就等于二 pi r l 加上二乘以 pi r 的 平方,那柱体的体积怎么求呢? v 等于 s h, s h 呢,就是表面积再乘以高就等于 pi r 方乘以 h。 好, 咱们接下来来看锥体,锥体的侧面积 s 侧就等于 pi r l。 锥体的表面积 pi r l 加上 pi r 的 平方,那锥体的体积呢,就是三分之一 s h, 那 它就等于三分之一乘以 pi r 的 平方乘以 h。 下面我们来看台体,台体的侧面积 就等于 pi 乘以 r 加 r 撇乘以 l。 看,一个 r 是 下面的半径,另一个 r 撇呢,是上面的半径。咱们继续看表面积 就等于 pi r 加 r 撇乘以 l 加上 pi r 方加上 pi 乘以 r 撇的平方, 它的体积呢就等于三分之一的 s 加上根号下 s 乘以 s 撇加 s 撇乘以 h。 这个公式咱们再来推导一下啊,就是 s 是 表面积吗?展开一下, 三分之一 pi 乘以 r 方加上根号下 r 乘以 r 撇加上 r 撇的平方,再乘以 h。 咱们最后来看一下球体,球体的表面积 就等于四 pi r 方,球体的体积等于三分之四 pi r 的 三次方。球体的公式比较好记,就是尤其是台体还有锥体,同学们要重点记忆一下。
粉丝2010获赞7.3万
相关视频
 09:59查看AI文稿AI文稿
09:59查看AI文稿AI文稿呃,这道题是一道单招的例题,几何,我们可以来看一下。这个他告诉我。第一问我,首先我们要读题,他说在棱柱 abc 杠 abc 一 中,他告诉我 a、 a、 e 垂直于底面, abc 能住吗?如果我的 a、 a 一 垂直于里面 abc, 其实也就是说我的呃,什么 c、 c 一, b、 b 一 都会垂直于 abc, 对 吧?这个其实对我们间隙是有帮助的。然后第二个,他告诉我, a、 c 等于三, bc 等于四, ab 等于五。 告诉我 a、 c 等于三, bc 等于四, ab 等于五。那么三四五直角三角形吗?勾股定律对吧?也就是说从这个条件里我们能得到的一个结论就是,我们的 a、 c 肯定是垂直于谁的, 垂直于 bc 的 吗?能理解吗?是因为你的 a、 c 方加 bc 方 是不是等于你的 ab 方,这个应该很好理解啊,十六加九二十五吗?对吧?然后 a、 a 一 是四。所以说这道题当我们读到这里的时候,基本上就这道题应该一点问题都没有了, 最麻烦最啊,那个最快最快的结果就我就间隙吗?间隙肯定是没问题的,他说让我们 d 是 ab 的 中点, d 是 a、 b 的 中点,它让我们正的是 a、 c、 e, a, c、 e 平行于 c, d, b, a, c、 e 平行于 c, d、 b 平行的话,我们是不是只需要在 c、 d、 b 里面找到一条直线和 a、 c、 e 平行就行了,对吧? 那我们找的话,因为 d 已经是终点了嘛,我们如果不傻的话,一定要去想终点,那我们就把 c、 b、 e 给连接起来, c、 b、 e 两连接起来,它和 b、 c、 b、 e、 c 是 不是一定有一个交点?是 o, 我 们连接 d, o, 我 们连接 d、 o, 这样的话,我们的 d o, 我们的 d o 是 不是一定是平行于 a、 c、 e 的 中位线? ok, 这就是我们整体第一问的一个思路,我们写下连接,第一问,连接谁?连接 c e, b 连接 c, e, b 交 b, e, c 于点 o 对 吧?交点 o 连 c, d o, 对 吧?我的 d o 就 平行于 c, d o 是 平行于 a、 c、 e 对 吧? d o 平行于 a、 c、 e 三角形中位线吗?如果你不放心的话,其实你还可以写一句话叫做终点吗?终点,终点,因为 d 是 ab 终点,终点,对吧?然后这个证出来以后,其实下面就是非常套路的一句话,叫做 d o 咋了? d o 属于这个平面 c、 d、 b 一 对吧? d o 属于平面 c、 d、 b 一 很明显吗? a、 c 一 不属于平面 c、 d、 b 一 对吧? 所以说你的 a、 c 一 就是平行于平面 c、 d、 b 一 的平行于平面 c 的 b 一 对吧?非常套路啊,非常套路的一个写法。然后我们看一下第二文,第二文它是让我们求正切值,求 ab 一 和 b b, e, c、 c、 e 的 正切值,其实这个正切值,其实,呃,本质上就是线面角呗,让我们求线面角的正切值。我们 这道题标准答案上给的是用几何法做的,我们就间隙吧,因为它的条件非常非常好,间隙,我们就用间隙的方法做一下 x 轴 y 轴 z 种,你看我们用间隙的方法去做的,我们用间隙的方法去做的。然后我们写坐标 a 点子坐标 a 点子坐标肯定是 三斗零斗零,对吧? b 一 的坐标 b 一 b 一, 这坐标,那肯定就是零斗四斗四喽,零斗四斗四,因为它告诉你 a、 a 一 是四嘛?然后我们, 然后我们 a b 一 就 a b 一 的坐标就写出来了,是不是 b 一 减 a 一, 零减三,负三, 四减零四,四减零四, ok, 然后他让我们写的是 bb bb 一 cc 一 的, bb 一 cc 一 的,我们现在要写的是 bb 一 cc 一 的发向量, 其实我们是要用法向量的,这个发向量的话, bb 一 cc 的 发向量其实是能看出来的,是不是其实就是我们 ac 啊? ac 就是 我们的发向量 ac, 所以 说它的发向量五可以写成 一斗零斗零,我的法向量是可以写成一斗零斗零的,它的法向量就是 a c e, 我 们用法向量来表示,用 n 来表示, 嗯,很明显啊,因为原因是法向量一定要和这个平面垂直嘛?根据条件其实我们能看出来它为啥是因为你的 a c 是 不是是垂直于 bc 的? bc 垂直于 bc, 又因为你的 a a 一 a a 一 a a 一 垂直于底面,谁? a a 一 垂直于底面 abc 实际是不是你的 a a 一 是平行于 c c 一 的,所以说你的 c c 也是垂直于底面 abc, 所以 说 c c 一 是垂直于 c, c 一 是垂直于 bc 的, 对吧? c c 一 垂直于 bc, 然后我们就能得到我们的 c c 一 垂直于 bc, 所以 说我们最终我们挣出来其实就是 a c, 这个是垂直于我们的,垂直于我们的谁? bc c 一 b 一, 其实这一这一对也可以不用写,不用写,然后然后把向量,我们是 cosine c 塔,其实这个值算出来应该是 cosine c 塔。值啊,但是你是用 cosine c 塔去算的,我们说 你先写一下 cosine c, 它是不是?我们套公式是 a b 一 法项, a b 一 向量乘以法向量比上 a b 一 的模,乘以法向量的模,然后我们这个的话,乘一下,上面就是负三了, 对吧? ab 乘以负三下,呃,下面你叫根号下,呃,十六加十六,三十二,对吧?这应该十六加四四以十六嘛,十六加十六,三十二,三十二的话加九十,十一,四十一、 九十九十一、四十一,然后再乘以个一,这个是不是就是根号四十一分之,根号四十一分之 三,对吧?根号四十一,其实要打绝对值的,打绝对值, 其实真正的这个值算出来,三 e、 c, 它是等于根号四十一分之三, ok, 三 e、 c, 它是等于四十一分,根号四十一分之三。那我们就稍微画一下三角形,因为我们要求这些值嘛, 我就令这个角为 c, 它 c, 它角叫做对边比斜边,对边比斜边,对吧?这个叫对边比斜边。现在然后我们要求邻边,邻边的话就是这个的平方四十一减去九, 呃呃,十一减九,九十十一二,对吧?三呢?写出了个二,你这个就是三,其实斜边就刚好三十二 有三十二加九十十一,四十一, ok, 没问题,那我们正切它按求的是 tan 的 c, 它正切值。正切值是不是叫个对边比邻边 正切这角对边比零边,对边比零边。这个开出来的话,三十二十六乘以二四倍根号二四倍,根号二乘以三,对吧?分之三,分子分母同时乘以根号二,嗯, 对,同乘以根号二,八分之三倍,根号二,对吧?八分之三倍根号。 ok, 这个就是我们用那个用间隙的方法去想的,间隙的方法去想的,然后这个就应该 应该没啥问题。这一块的话稍微我再写严谨一点吧。这一块的话是因为你的 a c 垂直于 bc, 然后 a c 垂直于谁? c c e, 对 吧? c c e, 所以 说你的又因为我的 bc 交谁交 c c e 于点 c, 所以 说就是 a c 垂直于 bc c e b 嘛? bc c e b, 所以说你 a c 就是 法向量,法向量对吧?法向量的定义就是它会垂直一呃,一个平面内两条相交的直线,所以说这道题最终的答案正确值就是八分之三倍。根号二,这道题你要用间隙的方法做的话,唯一需要特别去注意一个点,就是这个值, 这个我们是用 cosine theta 去算的,算出呃,算的时候用这个,但是算出来这角其实是 cosine theta 值,它俩是互余的,它俩是互余的关系,这个要稍微注意一下,然后这道题就没啥问题。
20小兴讲单招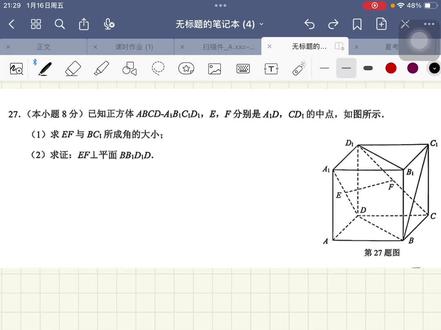 06:08查看AI文稿AI文稿
06:08查看AI文稿AI文稿同学们大家晚上好,今天晚上给大家更新一期立体几何的内容,那么今天的这两问呢?第一问是意面直线所成角啊,第二个是一个线面垂直。好,首先来看第一问, 那么异面直线所成角,我们去找角的时候,是要对这两条异面直线进行一个,哎,找平行线,哎,找到他们相交形成的一个夹角,是不是再去求值啊?好,那现在咱们来看一下啊,要求的是这个 e、 f 与 bc 一, 那很显然,他们两个现在是一个异面的状态啊,没有形成交点,所以我们要进行一个平移, 那么需要平移的啊,是我们的 b、 c 一 啊,这里可以做一条对角线连接对角线 a、 d 一 好,连接 a、 d 一 之后,这个 a、 d 一 和 aed 是 不是刚好相交于点 e 啊? 所以这个时候我的 a、 d、 e 就 和 e、 f 相交,产生了一个夹角,也就是我们的这个 d、 e、 f 啊,那在这里呢,你要对它进行一个说明。第一问,连接 a、 d e, a, d e 与 a e、 d 相交与点 e, 那 么这个时候呢,因为 d e、 c e 啊,它是平行于我们的 ab 的, 并且 d、 e、 c、 e 还相等于 ab, 所以 我们的 ab, c、 d、 e 为平行四边形, 那么它的另外一组对边就是一个平行的关系啊,所以 b、 c、 e 啊,它就平行于我们的 ad。 一 则 题目中,让你求的 e、 f 与 b、 c、 e 所成角就转变成了,哎,我们的这个角 d、 e、 f。 好, 现在重点是我要来求一下这个假角,那么求这个角的话,呃,用眼睛来看,它好像很像一个等边三角形,对不对?但是我们要进行一个严格的证明,那我们要去求一下它们之间的边长关系。首先这个 e、 d、 e, 它肯定是等于二分之一倍的 a、 d、 e 的 啊,那么因为这个是正方体,它的棱长我们是不是可以射一下?嗯,射棱长 为一啊,如果能长为一的话,那我的这个 a、 d 一 是不是就等于根号下一加一,也就是根二啊,也就是二分之一乘以根二,等于二分之根二啊,这是一 d 一 已经有了。好,那同理,我的这个 d、 e、 f, 它是不是也是对角线的一半啊? 啊? d e、 f 啊,也等于二分之一 d, e、 c 等于二分之根二,那这两个都有了,那 e、 f 啊,还差一个 e、 f, 你 看这个 e 点和 f 点,是不是现在都是中点啊?所以我再连接一下。我这个 a、 c, 那 是不是三角形的一条中线?嗯,又因为 e、 f 为中点, 所以 e、 f 啊,它就等于二分之一倍的 a、 c, 这个 a、 c 是 不是也是一条对角线,所以它也等于二分之根二啊?所以啊,我们这个三角形 d、 e、 f 为等边, 那么我们的所乘九九 d e、 f 是 不是就等于六十度?那这个题是不就证明完了?好,这是第一问,咱们接下来来看一下第二问啊。第二问是一个线面垂直好, e、 f 要证明它垂直于 b, b, d、 d, 它在这里。然后呢, e、 f 要好, e 点和 f 点啊,非常的特殊,它都是中点在三角形 a、 c d e f 是 不是相当于一条中微线啊?所以我们有 e、 f, 它是平行于 a、 c 的, 嗯,那么这个 a、 c 好 像更容易证明它垂直于这个平面是不是?那么对于线面垂直,我们有一个性质定律, 大家还记得吗? 性质定律啊,是怎么说的呢?如果我已经知道一个线和一个面垂直,那么和它平行的线同样也会垂直于这个平面,所以我只要能够证明 a、 c 垂直于这个平面是不就足够了?嗯,好,那我们一起来证明一下啊,因为 a、 c 它是垂直于 b、 d 的 啊,这个很明显是不是一条了?嗯,那还需要找第二条。又因为 我是一个正常体,所以我的棱是不是都垂直于地面 b、 b 一 啊,就垂直于我的 a、 b、 c、 d。 根据线面垂直的定义,我垂直于这个面,就要垂直于这个面内的任意一条直线啊, a、 c 包含于平面 a、 b、 c、 d, 所以 我的 b、 b、 e 就 垂直于 a、 c。 好, 你看,现在我已经有 a、 c 垂直于 b、 d, a、 c 还垂直于 b、 b、 e。 哎,所以啊,又因为 b、 d 和 b、 b、 e 它们两个都包含于平面 b、 b、 e、 d、 e、 d。 并且 b、 d 啊,交上 b、 b、 e 是 不是有一个点 b 啊,它俩是相交的,所以我就证明了啊, a、 c 它是垂直于我这个蓝色的面 b、 b、 e、 d、 e、 d 的 啊,没有,根据我们刚才的这个 e、 f 平行于 a、 c 啊,根据 线面垂直性质定律, 我们就有 e、 f 啊,它也是垂直于 b、 b 一 d, e、 d 这个平面的啊,那这个题是不就已经证明完啦?
190小脸喵讲数学 00:51查看AI文稿AI文稿
00:51查看AI文稿AI文稿立体几何不会做,今天教你一个妙招, 多点共线两面交,多线共面一法巧空间三垂悠闲大球面两点略乎巧。线线关系线面表面面成角线线表等级转化链策略, 能歌善舞假通桥。怎么样?是不是感觉高中数学的立体几何题都太简单了?我是果冻老师啊,在衡水中学呢,待了十几年毕业班了,每年呢都有数学满分的学生,教过的学生呢,都教我,数学救星,如果你还想学习更多的数学大招技巧口诀,报名我的高中数学急救包,带你学习数学的底层逻辑考试考什么 我就给你讲什么,我就教你什么。学一道题,会一类型,在有限的时间内查缺补漏,迅速上分。课后呢,还有九八五学长学姐帮你辅导,帮你做学习规划,只要你学不会更难!
 02:59查看AI文稿AI文稿
02:59查看AI文稿AI文稿根据二六年河北单招考纲,咱们看一下单招数学几何中求面积。今天我们通过两道题来学习一下正三棱柱的体积和它的侧面积, 那在这个里面的话,我们要知道什么是正三棱柱啊?正三棱柱是指的我们下面的这个三角形,是一个边三角形啊,是每条边都相等, 而且大家要在考试当中要会画图,这个图提前给大家画好了,所以在考试当中是没有图的,是需要你自己来画图的啊,别等考完才后悔,单招数学押题卷,提前帮你摸清公办院校的出题规律,练熟了,考场不慌,分数不丢。那在这个里面的话,那我们首先去看他给的条件, 他说是底面边长为二,也就是我们的这个三角形的边长都是为二啊,然后他的高为一,也就是这个高是为一的,那求他体积,首先我们要看这是什么体积, 那体积呢?要么是柱体,要么是锥体,要么是球体,他说是柱,那柱体的体积用 v 来表示,那他的公式是啥? s 就是 底面积乘以高啊,底面乘高, 那他的底面是一个三角形,是吧?变长为二的一个等边三角形啊,变长为二的一个等边三角形,那这个三角形的面积应该是怎么来求呢? 好,第一种求法是做高线,那第二种法,那我们用一个呃,三角函数里面我们用到的公式,三角函数里面三角形面积公式是不是二分之一? a b 三 c 啊? 哎,也就是知道角度就行,那他三条边相等,说明他们三个角相等,说明每个角应该是为六十度, 所以是二分之一乘,二乘以二乘以赛银六十度,这就是他的三角形面积。所以二分之一乘二,乘以二乘以赛银六十度,那赛银六十度等于两分之根号三,然后再乘以我们的二,再乘以二,再乘以二, 然后再乘以我们的二分之一,再进行约分,约分只剩下我们的根号三啊,所以他的一个底面积是等于我们的根号三的,然后高是为一, 所以是根号三乘一,结果等于根号三,所以我选的是二 b 选项。好,那接下来看第二题。第二题的话是这个正三楞柱的侧面积,那大家要知道什么是侧面积?侧面积指的是除了上底和下底,整个我们侧面啊,整个侧面,那侧面来看是三个面,对不对? 他的侧面底面边长为四啊,底面边长是为四,也就是说这个距离是等于四的啊。然后高是三,也就是说这段长是为三啊,那他的面积是一个长方形,长方形的面积应该是宽,对不对? 所以是四乘三应该等于十二。一共有像这样的面,一共有三个面,一个面,两个面,还有后面面三个面,所以十二乘三就是等于三十六, 这就是他的侧面积。侧面积就是除了上底和下底的面积,那如果考到是表面积的话,表面积就是再加上上底和下底,就是所有面的面积,那就叫做表面 积。另外关于单招数学常考的公式以及我的解题妙招,我都把大家整理好了,如果你还不知道背那些,一定要拿去看一看,背一背啊。
25单招资料严选官 01:21查看AI文稿AI文稿
01:21查看AI文稿AI文稿同学们大家好,我们今天来讲河北单招数学立体几何里面的球体。我们先来看题,已知球的半径扩大为原来的二倍,问,球的体积扩大为原来多少倍? 那我们就来想啊,球的面积表面积公式 s 等于四派 r 的 平方,然后体积公式 v 等于三分之四派 r 的 三次方, 对吧?那我们就从这个公式来看啊,面积是平方倍,体积就是立方倍,所以这个题半径扩大为原来的二倍,那么表面积就会扩大为二的平方倍,同理,体积会扩大为原来的二的立方倍,所以这个题我们选 c 就 可以了。 同理,我们来看第二题,已知两个球的表面积之比为四比九,问体积之比是多少?还是看刚才的表面积是四比九,也就是平方呗, 对吧?那几的平方是四二,然后几的平方是九三,所以就是说半径之比是二比三,表面积之比四比九,那体积之比就是 二的三次方八比上三的三次方二十七。所以我们这个题应该选的是 a 选项。 好,那我们今天先到这。
 20:01查看AI文稿AI文稿
20:01查看AI文稿AI文稿距离二零二六年单交春考最后一个多月,是你逆风翻盘的终极窗口期,如果此前的时光都被虚度,那这次机会你必须攥紧在手里,它直接决定了你能否拿到名校的入场券。 为什么说二月是最后的逆袭时机?因为一轮复习已经修委,你所有的知识漏洞、学习弱点都会在这个阶段暴露的淋漓尽致, 而剩余的时间刚好够你集中全部火力打一场精准的歼灭战。那些觉得单挑称考大局已定的人,早已提前弃局退场。但真正读懂考戏规则的人都清楚,现在才是实现弯道超车、彻底翻新的黄金习客。 正戏开讲前,闭上眼睛默念三遍,我必逆袭!永远相信相信的力量, 如果你此刻想发奋学习,却不机从何下手,或许拼尽全力却琪琪看不到想要的效果,那就去看我的置顶视频,加我粉粉群,我会亲自帮你分析成绩单,量身定计专属学习计划。好了,话不多说,直接开讲 啊,这个题呢,是一个这个解析,呃,这个 v t 几何啊 v t 几何的一个关于呃垂直啊垂直呢,咱首先咱呃做一个思路的分析。那这类题呢,一个思路分析呢,它是这样的 啊,我要去种线线垂直啊,我要种 l 和呃这个 m 垂直啊,那么我这个时候呢,就会去干嘛想到一个思路是什么?是说我要把这个 m 给它放到一个面当中,那我去想法去种 l 垂直一个面这个 r 吧。 那要垂直这个面的话,就需要垂直他这个面当中的两条线啊,这个两条线,那两条线的话,那这个时候呢,可能就要去正这个面,属于面当中的两条线,比如说一个 n 啊,然后呢?他呢?比如说,呃,垂直一个他的一个屁, 对不对?那垂直了这两条线,那我就垂直这个面,垂直这个面了,那我就自然而然就垂直这个面当中所有的线,那我就垂直了这个 m。 所以说整个的在你的立体几何当中啊,所有的思想都是这样,就说我要中线线垂直或者线面垂直,他的一个思想就说我必须得中线线垂直,那线线垂直的话怎么办? 把这个线,把其中一条线给他放到一个面当中,然后呢?呃,往往是这条这条线直接中,是没法中的,那我就呃,这个 换个思路,就说,我去正这个面,线垂直这个面啊,线垂直这个面,那这个时候呢,我就从这个面当中找两条我方便能求的啊,这个线啊,那就得出来这个线面垂直。好,那咱解一下这个题, 好,咱们看一下,刚才还有还有几个人说好来看一下。呃,那这个,呃, p a, b, c, d 啊, p a 垂直这个面啊, p a 垂直这个面, a, b, c, d 啊,然后呢? ab 垂直 ad r a b 垂直 a d, r a, b 和 a d 垂直 a c, a, c 和我的这个 c d 是 垂直的啊,然后呢?呃,角 a, b, c 等于个六十度, a, b, c 等于六十度。好, pa 等于 pb, 等于 ab, 等于 p, 等于 bc 啊,意思呢?是啊, pc 的 终点啊,那咱看一下这个 d 啊,咱正 啊,第一个,我要正这个 c d 垂直 a e, 那 c, d 垂直 a e 的 话,那我就正什么?呃,我这个 c d 啊,垂直这个,把 a e 给它放到这个面里边来啊,把这个这个 a e 给它放到面里来,那所以说我就想法去正,呃,它垂直这个面 啊,垂直个面啊, p a c 啊,垂直面 p a c, 那 我就要去正垂直这个面 p a c, 那 我就得去找它两条相交的线,那我就正什么 c d 啊, c d 垂直于 a c 啊,然后呢,再一个,我去正 c d 垂直于 pa 啊,那咱分析一下,咱刚才说了,题目当中告诉我 pa 是 垂直面的,那我的这个啊, cd 垂直 pa, 那 这个是已知的,那下边一个问题就说什么,我去想法啊,种这个 cd 垂直 ac 就 可以了啊, cd, 呃,和我的这个 ac 啊,那这个 垂直啊,那也是已知的。好,那所以说我就分析下,因为啊,这个 p a 垂直面儿面儿 a b c d 啊,呃, c d 呢,是属于这个面儿 a b c d 的 a b c d 啊,所以呢,那我就中出来我的 c d 啊,垂直于 p a 啊,这个第一个条件中出来了啊,然后下边又因为 又因为题目当中 c d 啊,垂直于 ac cd 垂直于 ac 啊,那你的等会说了,这个 a c 和你的 pa, 它都是属于面 p a c 的 p a c 的 啊,那而且呢,这里边 a c 啊,它交 ap 交 ap 于 a 点,也就是说呢,它是两条相交的线段啊,那所以, 所以我就能得出来 c d 垂直于面,垂直于面啊,这个 p a c 啊, p a c 啊,垂直面面 p a c 那 下面呢,我通过了线垂直面了,又因为又因为 a e 属于这个 p a c 面 p a c 啊,垂直这个面,那就垂直面当中所有的线,所以呢,我的 c d 就 垂直 a e 了。 好,通过这个题呢,咱就知道说我要去种线线垂直它直接去种是不好种的, a e 在 这, c、 d 在 这,它两个是不好种的,那我就转过来是什么?把这个线放到面当中来去种。好,然后再看第二个 这样问,他说让中 p d 啊, p d 垂直面 a, b, e 啊, p d 这条线垂直面 a, b, e 啊,这个面。好,那,呃,跟分享 啊,我要去中 p d 啊,垂直面 a, b, e 垂直面 a, b, e。 那 我就得找我的 p d 垂直于谁垂直于我找两条线垂直于 a、 b 而那我的 p d 而 p d 垂直于 a e 啊,我要正它这个面垂直它,那我就去找两条线段。好,那我去找 p d 和 a e 垂直,那我的 p d 和我的 ab 垂直。好,那然后呢?那下边我要正 呃它这个地方垂直啊,那我就想我怎么去去种它呢?那我就想到了把 p d 给它放到一个面,因为它现在你看到没有,就说这个 p d 啊和 ab 它两个现在 根本不是。呃,在一起没法去种,那我就转过来,我去种什么?我去种你的,把 p d 放到这个面里边来,那我就转过来,我去种啊, a、 b 垂直于面, 垂直面 p a d 啊,把 p d 呢放到这个面当中啊,那我就只需要用 ab 垂直面这个 p a d 就 可以了啊,那面垂直 p a d, 那 咱分析一下,那我看这里边 ab, a, b 是 垂直于 a、 d 的 啊,这个是已知,对不对?然后呢? a, b 是 垂直于 p a 的 啊,那那个那个,所以说,那我种出它两个来。好,那然后呢?你就说,呃我,我要去呃种 啊,我要去种它那个,呃下边一个,我要种它 p d 垂直 a e。 那 也是一样的思想,我就是干嘛把这个时候它两个也是直接去种 a e。 在 这啊, a e 和 p d 不好种,对不对?那我就想法转过来,我去种什么?我把这个 呃 p d 给它放到一个面来,我去种 a e 垂直这个面 啊,垂直个面 p c d 垂直个面 p c d。 好, 我要正。呃,这个 a e 垂直个面 p c d。 那 好了,咱看一下,那这里边 我的 a e a e 垂直什么?垂直 cd, 我 去想法种这个啊, a e 垂直 cd 就 可以了,那然后呢,我下边再种什么 a e 垂直于 pc 啊,那我去想法种这几个问题啊,也说呢,你看人的整个的分析的思路是这样的, 我要种它垂直这个面,那我就得垂直它里边两条香蕉的线那但是这两条香蕉的线呢?又不好种, 这两条香蕉的线不好种,我就转过来,我去把它这个线给它放上面当中 啊,我把这个 p d 呢放到这个面 p a d 当中,我去中 a b 去这个面啊,然后呢,找两条相交的线啊,这两条相交的线啊,然后这个也是一样道理,不好中,放到这个面当中,然后找两条相交的线。好,那然后呢,咱们看一下 下边儿 啊,我这边呃,证明一下。因为啊,我的 a b 等于个 pa 啊,等于个 b c 等于个 b c。 而且呢,这个角 b 角 abc 角 abc 呢?等于什么?等于六十度等于六十度啊,所以 我的 a c a c 就 等于个 pa ac 等于 pa 啊,又因为 e 呢,它是中点 啊, e 是 中点啊, e 是 中点之后呢,所以说我就能得正。所以说我的 a e a e 垂直 pc 啊,然后呢?呃,又因为 我这个这个 a e 啊,垂直于 cd 啊, a e 垂直 cd 啊,那我的,而且呢? p c, p c 好, 我的 pd, cd 它都是属于这个面 p c, d 的, 都属于这个面 p c, d 那 么 p c 呢?而且呢? p c 呢?交 cd 交 cd 等于 c 啊,那所以说,所以说我就能得出来,我的 a 垂直面 p c, d 面 p c, d 啊,垂直面 p c, d 那 又因为呢?我的 p d 因为 p d 啊,属于这个面 p c, d 好,所以说我的 d 用这个想要的这个边我就得中了,我就得出来说我的 p d 和我的 a e 啊,它是垂直的。 好,那等等,这个就解决了,也说呢,我要中它垂直,我中它两条相交的线线的话,那这个线我通过这个线放到这个面里边来,然后中 另外的两个键啊,那 p d 就 和 a e 垂直。好,那然后在上边重一下下边这个问题,然后写这。啊,因为啊,又因为。呃,这个 p a, p a 垂直于面 a, b, c, d 啊,那 ab 属于这个面 a, b, c, d 好, 所以所以说呢,呃,我这边就能得出来 ab 和 pa 垂直。 好,这是这个,那下边有问题,我要正它的这个这个垂直。呃,那 又因为啊,又因为这个 a b 垂直于 p d, a, b 呢?垂直于 p d 啊,那 p d 交 p a, 它交于 p 点啊,两条相交的线段那,呃,而且呢,我的 p d 和 p a 呢?呃,它都属于个。呃, p d 和 p a, p d, p a 呢,是属于这个面儿, 属于这个都是面当中两条相交的线,对吧?面 p a d 啊,那所以我就得证这个 ab, 这个 ab, 那 就垂直面面 p a, d 啊,它垂直面 p a d 之后呢?然后呢?呃,又因为你的这个,又因为我的 p d 是 属于这个面, p a d 的 啊,它属于这个面,那所以说呢,呃,我这个时候呢,我就能得出来,所以啊,我这个时候我就得出来 p d 垂直于 ab 啊,也说呢,呃,这个题啊, p d 是 属于这个面,那所以说我就得 p d 垂 ab。 那 所以说到这我的这两个条件就已经得正了,那我就直接可以下结论了啊,所以 啊,我这个 p d, 那 就垂直于面, p d 就 垂直面 ab 一 啊,所以说你看这个题,这个题他考察的一点是什么?就说我要中线,你看咱的刚才这个,这两个的这个思路分析啊,这两个这个思路分析啊,这两个这个思路分析是很重要的一个思想,他的一个思想是什么?就是你看,呃,我要中线垂直 直接种,比如我这个 c d 和 a e 不好种,不好种的话,那我怎么办?给它放到面当中,我把 a e 呢?给给它放到面当中,我比如说呢,我把这个地方给它放到面当中,那我去场花种什么?我 c d 和 和我的 p a c 垂直啊, cd 和 p a c。 那 这么说呢,我本来需要去种 a e 的,是本来是要去种 a e 的, 但是我的问题就给你转化了,我不需要关心 a e 了,因为那个 a e 也是属于 p a c 当一个面,那所以说,哎,我只需要去种 它垂直于 ac, 它垂直于 pa 就 可以了,我的问题就本来由它,我就给它转化成了 求这个啊,那求这个的话,那这个时候这两个是简单的啊,很能简单的中出来,我中出来它垂直这个面了,那你是这个线是属于这个面当中的,我就得中了啊,那你看这个题的思路也是一样哎,我要中这个 p d 垂直的面 这个面儿,那我得重换把 p d 垂直染成线啊,垂直它好,垂直它不好重,直接重是没法重的,对不对?那我就转过来,把 p d 呢给它放到一个面儿当中。你看,我把 p d 给它放到了这个面儿 p a d 当中 啊,就我不再去关心你 p d 是 怎么样了,我只关心你这个面儿了啊。你看,我把这个 p d 给它放到面儿 p c d 当中。 好,然后呢?我一转化之后,那我就干嘛?你看,我就只需要找到在 p a d 当中,我转化了,我不需要关心 p d 了,因为 p d 它不好用嘛,我就转化成了和 a d 和我的 pa 它们这两个之间的关系。那我这个呢? p c, d 我 也不需要关心 p d 了,我只需要关心 cd 和 pc 啊这两个的条件就可以了。那么我就通过种了叉了,我就种出这个面来了。好,他这个面成立了,那我自然而然就垂直个面当中的所有的线了,那我自然而然就得到这个这个结论了。 你看,这个也是我垂直这个面了,那我自然而然就垂直面当中所有的线了,那我就能得出我的想要的结论来 啊。所以说呢,这类题在解析几何当中,包括你的这个一体几何这种证明题当中, 在垂直关系当中,它用的是非常多的。一个问题就是,我一旦让你去中线线垂直,你看线线垂直不好中,我干嘛把这个线给它扔到一个面里边来,然后呢?找这个面当中另外两条相交的线啊?好,这个题就讲这线。
11解忧单招数学松哥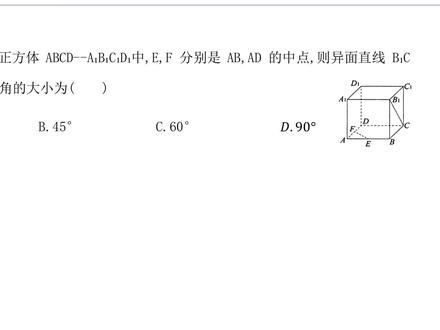 01:40查看AI文稿AI文稿
01:40查看AI文稿AI文稿哈喽,大家好,我是汉辰大招张老师。今天我们通过这道题来学习一下线和线之间夹角的问题。在这个正方题里面,他说 e、 f 分 别是 a、 d 和 ab 的 一个中点,也就这就是我们的 e、 f 这个虚线位置,对不对?这是 e、 f 的 位置, 然后他让我们找 e、 f 和谁之间的夹角和 b、 e、 c 啊,这个斜线 b、 e、 c 之间的夹角,那如果遇到线线之间夹角问题,我们必须让线和线连接上才有夹角啊。所以在这个问题里面,你又不能随便进行移动,要怎么进行平移啊?平行移动啊?平移 e、 f, 它首先第一个位置可以移到的是 b、 d 这个位置对不对?因为 e、 f 是 b、 d 的 一个中位线,因为它是这一一半的一半,对不对?所以它是 e、 f 时的中位线, 然后移到这以后,我们显然还是没有夹角,那我们再进行移动,可以给他往上进行平移,移到 d 一 和 b 一 的这个位置,此时是不是产生夹角了啊?那此时这个角就是我们的一个夹角关系,那这个位置我们连成两条线,还看不出来角,那我们再给它连接,把 d 一, 然后连接到 c 的 位置,连成一个什么三角形,那我们来观察这个三角形,那这个是我们要求的角度啊。这个三角形里面,你来看这个 bc, 然后是不是我们侧面的一个对角线, 然后 d 一、 b 一 是不是我们顶面的一个对角线?然后 d 一、 c 是 不是我们后面的这个面的对角线,也就是他是三个面的对角线,说明他们三条边相等,所以他们这个夹角应该为六十度,所以我们选的是 c 选项啊。
55瀚宸单招-张老师 04:46查看AI文稿AI文稿
04:46查看AI文稿AI文稿好,大家好,今天呢给大家讲一道例题几何的小题。 做这种题,一般呢我们就画一个具体的图形,例如正方体啊,长方体啊,呃,我们在说这些问题的时候会更好一点,把一个具抽象的问题具体画。 首先我们假定这个右边这个面是 alpha 底边这一个底面,这一个面呢是 beta, 那 么它的交线就是 l, 就是 这一条。 好,那首先呢,他说阿法内,阿法内右边这个面,阿法内的直线 b 垂直于这个贝塔内的这个直线,例如举个例子是这一条,这条 b b 跟 l 是 平行的,所以 b 是 跟这个 beta 是 平行,所以呢,它不一定啊。好,那首先呢,这里面 alpha 内的已知的直线,已知的直线 b 垂直于 beta 的 无数条,它只是无数条,不是任意, 所以说已知直线。你举个例子说这个 alpha 内,那么是,假如是这一条 就是这条,那么这条我们知道这一条呢?假如这条是 c, c 是 垂直于右边这个面的,也就是垂直于这个 alpha 的, 然后呢,这里面的一个这一条,这一条角对角线呢?是这个面阿法里面,所以这两条直线会互相垂直,那么跟他互相垂直有很多条,例如说只要跟 c 平行,这些所有的线都可以,所以他是允许存在的, 那么他说 alpha 内的任何一条 b 垂直于,那么说错了,应该是,呃,这个与那个 a 呢,有点相似,有点相似, 对不对?可以,假如说找一个 b, b 是 被 alpha 里面的,那么它会被,它不一定是垂直于这个贝塔,反而是平行。 好,然后他说过这个 alpha 内的任何一点, alpha 内的任何一点做与 l 的 垂线,其实我们可以找什么呢?其实我可以过这个点,然后做一条线,假如这一条线是 r d, 这个点呢,确实是在 alpha 内的,然后做了一条过这个点,假如这个点 a a a 在 alpha 内,然后这条 d 的 线,这条线呢,跟这里的 l 是 垂直的,也就是 d 是 垂直 l 的, 且呢这个点 a 呢,是落在面 alpha 的, 但我们可以推出的是这个 d 啊, 确实会跟这个面这个贝塔是平行,不一定垂直,所以这个 d 呢,也就错了。那怎样才会垂直呢?根据我们这个面面的这个 垂直的一个性质定理来说,它是这样的,假如是阿法,这是贝塔,这个是 a 了,我们一定要是过这个点,过这个交线的其中一个任何一个点,然后在阿法内做一条线,垂直于 这个 l, 也就相当于说我在这个 a o 呢,是一定要垂直 l 的, 然后 a o 呢,是落在面 alpha 的 啊,然后这一个两个面已经是垂直了的,然后这两个面的交线是贝塔,那满足这个特征呢?我们确实能够得出 a o 呢,就垂直于面贝塔, 但是呢,对于这个 d 选项来说,就缺少了这条直线到底有没有在这个 alpha 内,也就相当于说 它这个虽然其中有一个点是在这个 alpha 内,但是它并没有说向这个 l 做垂线,所以就不一定好。今天呢,我们就讲到这里。
14伟帝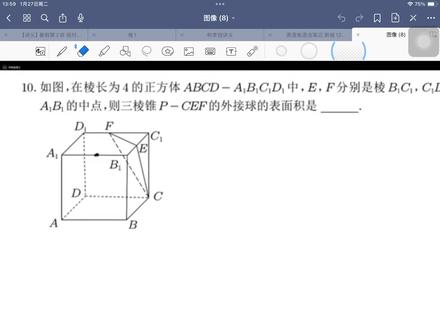 03:44查看AI文稿AI文稿
03:44查看AI文稿AI文稿ok, 我 们看这道题啊,这是一道呃,求了一个外接球的题目,然后它是能长为四的正四面体啊,这正方形,然后 a、 b、 c、 d, a、 b 中 e、 f 分 别是 b、 c 和 c, e, d, e 的 中点, 若 p 是 棱长的, ab 的 中点,你看 ef 是 中点吗?就这个地方这边,然后这个这个地方就是 p 吗?你看,然后他这把棱长是二四吗?对,这个地方是二,对不对?二二。然后他们的平方这是垂直吗?垂直的话就可以推出来,这个地方是二倍根号,二,对不对? 然后的话,然后连接这个 p, 这个地方他也是垂直吗?这地方也是等于二倍根号,然后这个地方 e、 f 的 话是等于这个 a、 d 对 不对? a d 的, 它这是等于个四,然后你看二倍根号二的平方加上二倍根号二平方是不是等于四的平方?这个地方是垂直, 然后我们做线下来,既然知道这是垂直的话,垂直所对这个边他的中线对不对?比如说为 o 一, 他就是那个外角圆形,然后我们去找这个球心, 球形的话就在这条线往下面延伸的这个点上面,假如这个点我们现在不知道吧?是为 o 吧?那么说我这个地方要把这个 b p 往这边擦一点, p 点在这里好吗? 然后连接,你看有这条直线,对吧?他是是为一个这个下面这个长度,对吧?就 o 撇下面这个长度是为 x, 对 吧?那么这个地方就是一个什么呢?这个地方应该是一个 四,呃,四减 x 对 不对?四减 x, 对 吧?然后这个地方连接这个地方是一个 r, 这个地方是它的圆心,然后这个地方是四 x, 这个地方是一个中线吗?因为这是中线吗?这个地方是一个 r, 对 不对?所以就可以得到一个方程,就是四减 x 的 方, 加上那个,呃,看四等于那个 r 方嘛?然后再连接这个三角形看,往下面坐下来,对不对?这个地方坐下来,这是 x, 对 不对?然后连接这个 c, 比如说这个是为 o 二撇,好吧?然后这是 c c c o 二,对不对?你看 c o 二是不是?你看这个地方 a c 的 话是对角线嘛? a c 对 角线是等于四倍根号二,那么这这个是它的一半,那是不等于,就是就是 c o 二的话,它是等于一个根号二倍根号二的,对不对?所以说的话这个地方是二倍根号二, 然后这里再连接 o p, 连接 c, 这个地方也是一个 r 嘛?所以说你看这里可以得到第二个方程,就是 x 方加上一个 八,等于一个 r 方,然后把它连立,好吗?这是一个四减 x 方加四,等于 x 方加八, 然后这边约掉一个四,这里约掉一个四,然后这里十六减去八, x 加上 x 方,等于 x 方加四,然后约掉一个 x 方,这地方就是一个,再再约掉一个二,这是十二十二,就等于八 x, 然后我们再约掉,再重新出,重出一个四,那这里是一个二 x, 这是个三,这 x 就 等于一个三分之二,然后我们的那个, 对吧?然后我们可以就可以求列 r 方了, r 方的话就等于一个 x 方嘛?是等于四分之九,加上一个四分之,你看八,是吧?四分之三十二,对不对?就等于四分之四十一,对吧? r 方是四十一,然后那个三分之四 pi r 方,对不对?就等于那个圆的面积嘛? 三分之四乘以一个四分之四十一,这里约掉一个四,然后这里就等于一个,这是派二派八方,对不对?就等于一个三分之四十一派方。所以这题就是三分之四十一派方,听懂了吗?
 07:17查看AI文稿AI文稿
07:17查看AI文稿AI文稿hello, 大家好,今天的话再更新一期力题几何的这个思路的,就是最后这个求正弦值,求左乘角,哎,求正弦值,余弦值之类的东西啊,主要是更新思路, 那么我们之前其实学过很多期了,那这期主要是一个总结视频, 那面与面的夹角,我们会求面与面的夹角,怎么去求呀?是不是在交线的上面找一条线做垂直,做垂直,这个角就是我们要求的面与面的夹角了,可以吧,这是最常见的,只需要正垂直, 垂直。好,最典型的一个题目就是这个,我们来看一下,它要正的是 p a b 与 a b c 垂直,那这个怎么正呢?我们过 c 点做 ab 的 垂线。 好,那有一条线了,然后再把这两个连起来,肯定是它俩连起来啊,不可能是别人。好,所以,然后这个 p c p d 这个角即为二面角, ok 吧?好,所以我们要怎么写呢?所以要先证明到 c d 垂直, c d 垂直 ab, 这个是我们做的,做垂直,然后接着连接 p d, 这个要垂直它首要任务是正它, ok 吧?然后这个是在前面的有一个立体几何大底,里面有, 就是立体几何大题解析里面有,大家可以去看一下。好,这是面与面的求二面角正弦值,那求正弦值就是对边比邻边呢?对不对?好,这是面与面,接着是线与面,还是换一个面, 接着是一个线,那线要与面求交点,我是要做它垂线的,做它垂线下来,哎,叫这个垂线的这个点啊,这个垂线,然后与这个面的交点,然后连起来,求这个角,假设这个是 c 塔吧, 如果能证明到这边垂直它,那这两个连线,这边所成的这个角,我就叫做线与面的夹角。好,最典型的例子是这个题,来看一下啊, 现在要证 pa, pa 与 abcd 与下面这个,你看是不是跟这个很像呀, 反正也是一条线,然后他要做垂线下来。哦,这个垂线怎么做?很好做,连接他就行,连起来。这个题目大家可以看一下,答案的话,自己小圆搜题吧。我这边没有对, 你只需要证明谁证明这是它的垂线就行,这里会垂直下面就 ok 了。好,这个也比较好,正因为这边给了两个边 p b 等于 p d, 所以 它会垂直下面,然后以及它垂直它,所以它垂直这个面,大家可以去做一下这个题。这个题还 是啊,我觉得还是挺重要的,大家搜搜小圆搜题,不会的话,小圆搜题啊。今天只讲思路, 它做垂线下来,证明它是它这个面的垂线, ok 吧,所以求的就是这个角。哦,我求这个角,那就是要求什么?锁绳的角嘛?我求一个 tanger, 对 边比邻边,然后看一下 tanger 等于多少,然后看一下它等于几对不对。 ok, 这样就能求 seat 了。举个例子,比如说 tanger seat 等于多少呢? tanger 这个角假设等于根号三,可以吧,所以 seat 就 等于六十度了,对不对? tanger 六十度等于根号三嘛?好,这是这个好,除了这两种之外,这种是我们更常见的。为什么呢? 这个哈,这是这个面,然后这是这条线。好,线与面有一个交线,你可以理解为这是线与面的交线,可以吧, 那这个就不好做垂线了。为什么?你看这个线与这个面做垂线,你做到哪里去啊?垂直他吗?啊?你怎么知道是垂直他呢?你怎么不说是垂直他呢?对不对?现在要证明的是 a c, 这个 a c 与 p b c 换个颜色, p b c, 你 做垂线吗?哼,这个线做垂它还是垂它?我不知道怎么垂呀?我不知道这个垂到哪里呀?能理解吧?我做垂线正常做垂线下来吗?那我哪知道是垂这还是垂,这你不知道是垂哪里?为什么?刚才那个可以啊? 刚才这个垂线很明显啊,这个垂直下面这个面,所以它是垂线,这是垂点, ok 吧? 啊?这是垂足啊,不是垂点垂足啊,这里不行啊,这里不行,所以我要改变方法,我就不要这样子了,我怎么办呢? 我跟正面面一样,面面怎么正的?证明这条交线首先这边垂直好,然后再垂直它,这个就是那个角了,这边也同样的,这边你只需要证明它垂直它, 然后以及这个面里面还有一条线与与这个交线垂直, ok, 这个角就是所成的角。好,所以我们遇到这个,遇到有一条交线的 怎么办呀?就是把这个垂直它以及这个垂直它就 ok 了,证明到这个就万事大吉了, ok? 不? 好思路整理一下啊。首先面与面肯定是直接交线,这边引出两条线垂直就行,引出两条线垂直就行, 接着是线与面,如果线与面的话,一般情况下如果能正到垂线的话,那就直接正到垂线,然后再 taylor 或者 cosine sine。 好, 如果是没有的话,没有那个有交线, 线与面,有交线,有交线的都是干嘛?这这两个,这个交线垂直它和垂直它就是这个垂直下面和这个垂直下面,然后所求的角就是这个角, ok 吧? 那这边所求的角就是这个角,这个角等会添着一下 sign 的 话,哦,正弦是不是 sign sign 一下, ok 吧?是不是很简单? ok, 那 这就是一个就是证明求这个角的一个思路啊。思路 一共就这三种情况,没有别的。我跟你说没有别的也不要用那个空间向量了,就是之前我那个专题里面讲什么用空间向量啊?很难,因为用不到,所以我说那个难,知道吧? 就当时我就没仔细去做,当时我用的都是那个向量法,空间向量法,但是现在就讲了这么多,我还是发现几何法比较好做一点,所以大家都学几何法就行。好吧, 而且他证明过程都不难啊,你看这三个过证明过程难,很难的。正垂直嘛,这边也是正垂直嘛,他垂直下面嘛,垂直下面这个面嘛,这边也是正垂直嘛,他垂直他,他垂直他嘛,对不对?好,那么这就是立体几何的这个亚洲体,就是 就这样说,一定就结束了,应该还挺简单的吧。好了,那感谢大家收听啊,祝大家明天有个比较理想的成绩吧,拜拜。
419番茄学数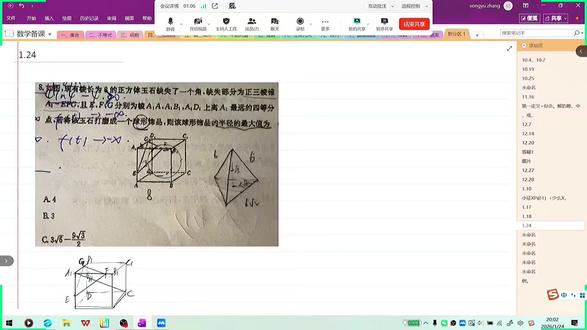 19:30查看AI文稿AI文稿
19:30查看AI文稿AI文稿这种题他有两个考法,一个就是你这个正方体正常,它本身它有一个自己的内切球,那假如你截的这个角很小, 那我是不是不影响我未来这个玉石的内切球啊?对对对,嗯,所以这个是咱第一个要判断的事。 如果这个角也就是这个点到这个面这个等边三角形的距离也就是这高吧,这个距离,如果是 这个已经侵占了,这个侵占到圆里了,这个时候就,那就题题目难度就增大了。如果他这个距离他小于这个没有接触到这球面, 那,那他的结果就还是正常的正方体的那些球半径,嗯,是,所以这个我们得先算一下这个, 那这个怎么算呢?我们可以因为你正常啊,怎么看他这个亲没亲入到这个里面。那些球球面, 假如正常这个大正方体的那些球球心是 o 一, 那么这个角是多,这个,这个是 a 一 啊,这个 a 一 o 一 长度, 然后我再减去这个小高,剩下的这就是 h 吧,这个点是 h, 那 剩下这个 o e h, 我 跟这个大 r 去比较不就完事了? 嗯,对,嗯,因为这个 o e a 一 是已知的,而这个面点到面距离这个这个高也是已知,我一减去它, 那如果它大于 r, 那 压根这题就简单,就这角切不切无所谓了。那如果它这个这个 o e h 小 于 r, 那 这题就增大难度啊。所以我就算了一下, 先算这个 a e h a e h 呢?这个用等体积法就好了啊,这个本身的体积是这个这个强扭体啊,三分之一乘以二分之一乘以六,乘以六乘以六, 然后它还等于你用 a 一 做顶点,底面等边三角形四分之根号三,再乘以六倍根号二的平方,是不是 a e h 就 出来了? 嗯,嗯, a e h 出来了,是二倍根号三。然后我现在还得求 o e a o e a 是 不是二分之一 a e c 啊? 嗯,就是 a 一 到整个中心的距离, a e c 是 体对角线,是八倍高三,所以我除以二就是 o e a 了。 o e a 一 o e a 一 是四倍高三,所以 啊,这是,这是这个长度是四倍杠三,然后这是二倍杠三,所以我这 o e h 是 不是二倍杠三?嗯,我还得算一下小 r 这个大 r 正方体内切球, 大 r 是, 嗯,四,哎,大 r 是 四,这一半变长了,那它是不是小于四啊?嗯,是的。 所以你这个题是不是啊?对,就变难了,难度升级了啊。也就说这个面,他是这个面,是会侵入这个这里面的那些球的, 所以这实际那些球肯定是比他小的。嗯,对,嗯, 你要是在这,假如这里面本身就有一个那些球,我在这块砍一刀,砍个甲,不影响那些球。但是现在咱算了一下,我发现这个面啊, 到这 o 一 的距离是二倍杠三,比这球半径还小,所以说明我在这砍一刀的话,他一定会把球砍掉一些。对,所以你要求的这个那些球就肯定是比这个本身这个球 o 一 是要小的。嗯, 然后啊,怎么思考我球比他小啊?关键我这球在哪呢? 这个就是这题的一个小难点。嗯,因为他这个图形之前我给你讲什么外接球、内接球啊,我分了什么圆锥、圆柱系列、圆台系列啊,考察中锥什么,但是这个很明显,这是一个不规则的几何题, 但不规则几何体他还得让你求出来他的那些球原形在哪里,进而求出半径。嗯,那你,你到这,你思考到这没?当时, 对,当时我就是,我,我就是知道他那个不能直接拿那个球的那个半径来算,但后面我就不知道该怎么做。就,还是啊,他,你就得思考了,他这个球心到底在哪。 而且,嗯,我如果想让里面的那些球最大的话,我这个球得跟几个面相切,那几个面相切就得思考这两个事。 然后我,刚才,我是,我是下午做的题。啊,我是怎么想的呢? 因为你切的这个角,他是一个标准的比较对称的一个图形,嗯,对,切的都是六六六啊,所以我是这么想啊,我当时我就一个想法,我如果把这个角当做正方题的,正方题的底呢?我给它倒过来, 倒过来,去想啊,你这么去想的话也行啊,我,我把它这个切这个洁面当做底座。哦,我知道你的意思,那我就画了个小图啊。嗯, 我现在得确定球心 o 的 位置,然后我,我就想,那,那他球心 o 得在哪?另外他怎么才能让里面球最大?他得跟谁相切?这是个难点。嗯,他可以,你看我,我可以跟这个底面相切。我跟顶面是否相切呢? 因为现在有好几个面啊,你这个,这是一个三角形结面,然后同时呢,这个五边形的结面是不还有三个呀?啊?前面上面还有左面,然后背面是不还有三个完整的正方形? 嗯, c d 一 和 b c 一, 还有 a c 这三个完整的正方形啊?一共就六个面, 往上面三个五边形,这里还有六边形加上一个三角,一共七个面了。但是你把它倒过来之后,我就,我就明朗了,我把这个打把它当做底之后,你如果想让里面的球最大, 那你只需要让他在上面这三个完整的正方形跟这个球贴边就行。相切就行,既得跟上面贴上,这三个正方形面相切贴上,而且还得跟底面你切的三角形面贴上,这样就最大。 嗯,但是我当时就是想他,他可以就是给你所有的面都切吗?而且啊, 而且怎么确定啊?而且它你还得确定球心在哪,嗯,我由于把它颠倒过来了,所以我你这 c 一 跟这底面的三角形的这个连线,它是一个类似于比较对称的吧?它是一个这对称,这对称,这对称, 嗯,它是个对称的图形,所以球心它肯定是在这个一对角线上。 a、 e、 c 连线,嗯,你把它补起来,这底面这个这个点就是 a 一 了,这上面是 c, 嗯,所以你如果真要是满足五个面相切,那个是 做不到。嗯,我想让里面球最大,我只需要让这球上面这三面顶上,同时底下、底下这个面就已经满到最大了,就不用管旁边这三个五边形了。 嗯,是的。嗯,而且啊,这个 你如果严谨的证明呢?那确实是你可以求完之后再证明他能不能跟这个这五边形贴上 啊。假如你按照就是你做这种题,一种思路就是,那我先让他顶,都顶上,顶上这三个正方形面,顶上,底下这三个面我也顶,上下相抵,都顶到头了,我觉得这时候球是最大的了。然后你可以验证啊,你看看这个,他跟这个侧面这五边形贴没贴上, 这是如果你要贴上的话,你如果要非得满足这,这你得看以谁面为主,我现在以这仨正方形面为主。你那个思路呢?是以五边形面为主,看哪个球最大? 嗯,当然的,计算量其实就挺大了。嗯,因为你得相当于算两道题,然后这还是一道选择嘛。我是猜测,我就是觉得 他踢对角线,首先这个,这个,这个球形肯定在踢对角线上,而且呢,我是让这个面上下相抵了,我看能不能跟这侧面贴上就行,也就这样。嗯,我当时我就思考到这,嗯, 而且啊,他一定是贴不上,因为你如果满足我说下你的思路,你是让这六七个面都得相切,那不行啊,你七个面,你这六个面相切,那你不就是成了大球欧一了吗? 嗯,对,这一句话就能这个,呃,否掉你那个想法,你想让你这五边形切,然后还能跟这正方形相切,那你只能有一个球,那就是大球欧耶。 嗯,但你还做不到啊,他因为咱已经推出去,球肯定比大球小啊,所以咱只能保证这仨正方形面 贴上底下这三角形面底上就完事了,他跟这个面是肯定是碰不着的,也就是说就是尽可能他让更更多的面贴着,就是他最大的数。对, 他肯定啊,咱求出这个小球肯定是贴不上正面,因为你看,我把这球稍微放大一点 看啊,稍微放大一点,这不就变成大胸 o 一 了吗?这个时候他是跟前面这五边形跟正方形全切上,但是咱比他小,咱比他小,只能是就这么切了,因为就,就是他这个这个角呢,就这个这个部位, 对,变小了,变小,然后跟着三角形面切。嗯,那就这一头我就不变呗,这仨正方形我不变。哦,你看, 而这个时候,他是跟这前面五边形也切上,那我现在变小了,肯定跟前这五边形,这三个五边形这边搭不上。嗯,但跟后面那切上,而且他还在这个对体对角线上。嗯, 行,现在确定这个 o 的 位置啊,这个 o 位置就是在这个 c h 上。嗯,现在还有一个问题就是,嗯,那我知道相切了,我怎么求出这个 r 呢? 嗯,是这种题套路啊。嗯,你这个,你像咱们正常讲那些球半径就是用等体积法, 嗯,是的,什么三 v 二小 r 等于三 v 比上 s 表,嗯,对,但是这个呢,它是跟所有面都相切,那肯定咱用不上,没法用这东西。嗯,嗯嗯,你这就是得独立去单独去思考了。 然后我是怎么想的呢?你这个图形切完一个角之后,这个这个几何体它是不是也是一个左右对称的? 嗯,对,我沿着这个 e 和这是 g f g f 中点, 假如是 k 吧,我沿 e h, 我 这么切一刀,我就沿对角线,我这么从上往下切一刀, 就只考虑结面就行。嗯,因为啥呀?因为我这球它本身就是跟这三角形面,跟这后面这三个正方形面, c d c d b、 c b c a b c d, 这是个对称的,这这仨面搁这抵着呢。然后, 哎,等会我说啥了啊?对,你这球它是左右对称的,如果这块切一刀之后的话,这球也是不也是一分为二给切开了?嗯啊,咱看一下,我画个图, 就是沿这个体对角线,我从上往下切,那你这里面,你要求的这个 那些球是不是也随之一分为二了?对对对,哎,你球本身也对称的一些,而且你球心就在 ac 上,所以你球这一分为二变成两个半球了,所以这个时候球的结面 是不就是它的轴结面了?嗯,对啊,所以你要求的半径不就求这圆的半径就完事了呗。嗯 嗯,明白。嗯,就是他,因为他是一个对称的,而且球心位置我知道,球心位置我知道了, 然后球我得求大 r, 大 r 小 r 怎么求啊?你一分为二之后,球也一分为二,所以就找不到了。他最大那个轴结面那个圆,嗯,能是沿中球心这么一切就找到这球球面了, 那里面的最大的圆。嗯,所以我就画了一个图啊,但是这个画图你得会,你也得把这圆画画明白了。 那怎么画这个圆?也就是我刚才球是跟这几个面相切,跟三个正方形面,跟三角形底面相切啊。嗯,那么咱画出这个切完这一刀之后,我这圆又跟哪条边相切? 这个时候就用到这个事了,那球跟谁相切?那你切完之后,这圆它就跟哪个面的边相切不就得了? 对,我原来我这球是跟是不是有个底面 a, b、 c, d, 嗯,然后还有一个,还有两个侧面,这个 b, c, c, b 和后面背面 c, d, d, e、 c。 而咱们切这一刀是不是跟这俩侧面,那是不是根本都没关系啊?嗯,所以 你看我切这一刀,我都没碰着我这个 c, b, b, c 和 c, d, d, e, c, 就 只碰着了底面了, a、 b、 c、 d 了, 所以我画的图是因为你球是跟这三面相切,但是你切完这一个,你把这洁面提取出来,它就只只有底面了,就底面 a、 b、 c、 d 了,所以我就跟底面底边 a、 c 相切,所以我的图也是这么画, 我只要保证我这画的这个圆跟这个三角形洁面 e、 k 和底面 a、 c 相切就足以。嗯, 然后剩下就好办了,我画了一个圆,然后这是大 r, 这是大 r, 然后这个长度 c h。 刚才求出来啊, a e, 这总长 a e c 是 八倍根号三, a e h 二根三,所以 c e h 就 六根三, 所以这是 r, 然后这就是六倍根号三减 r, 然后这也是 r, 然后我原本想列勾股定律的,然后我突然发现这个长度我也不知道,嗯,因为这也不是终点,他肯定是终点不知道。嗯,那球缩小了。嗯,对对对,所以也很简单啊。 那我又想了一下,这个,你看我看我笔啊,你这个是倾斜 o, 然后这往下做一个垂直, 那这个,这是不是能想到啥了?这是不是一个啊?相似,嗯,对对对,所以我是这个竖边比斜边,这个大竖的边比这大斜的边。 嗯,你就是你勾股定,你列不出来呢,你就得找你看看直角三角形嘛,你看看能不能用这什么塞塞塞啊,找关系,而塞塞塞其实是值得的。就是就是,相似都一码事。嗯, 所以算谁的啊?或者是这个小 r 比上这个棱长是八啊, r 比八,等于这斜边比斜边六倍杠三减 r 比上八倍杠三。 嗯,啊,这题就搞定了,这大 r 就是 这球的,嗯,是解漏了。对对对,是这个。
18消失de光年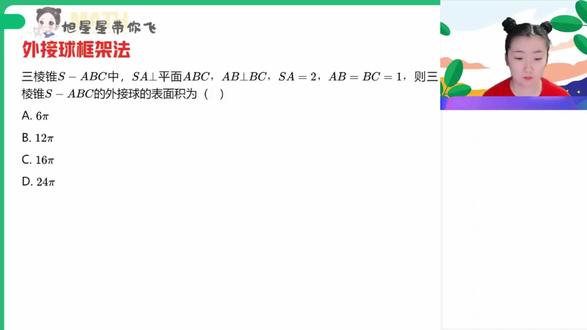 01:24查看AI文稿AI文稿
01:24查看AI文稿AI文稿像我们这种计算,哎相关的棱锥的外接球的 表面积,也就是其实要求我们外接球的半径,对不对?哎,这种题目一定要看它给你的锥到底具有什么样子的识别点。像 s a 垂直平面 abc, 我 们有一组线面垂直,对不对?然后呢? ab 又垂直 bc, 所以 底面是一个二 t 三角形, 这是一个垂直。然后呢?哎,他有一个线面垂直, s a 垂直,他垂直在了我们非直角顶点上,这也是属于我们长方形模板的。你只要找到这三条哎,分别跟垂直相关的线段的长度就分别对应了我们原先长方形模板的长宽高。 s, a 是 二, ab 等于一, bc 等于一,所以我们直接用我们的长方体模板面积公式,根号 a。 呃,半径公式, a 方加 b 方加 c 方,开根除以二就可以了。那 a 方 b 方 c 方就是这三条边, 一加上一加上四,开根除以二等于二分之根号六就是我们的半径。要让你做表面积,就是四派二方,对不对? 哎,计算一下,四派乘以我们的四分之六,哎,约一约等于我们的六派,答案就是 a, 超级容易,只要你识别对了我们的这一类识别点就可以了。
17雅婷老师 05:00查看AI文稿AI文稿
05:00查看AI文稿AI文稿今天要讲的这道例题几何题考的非常的好,首先他的题型很少见,其次他考察了孩子们的一个空间想象能力。这道题来自于东城区刚刚考完的单选压轴, 我把选项直接去掉了,咱们当一道填空题来做来看这道题目,他说这是一个棱长为一的正方题,然后这个正方题分别是 a、 c、 c、 e、 a e a 一 b c、 d e 以及 a、 b、 c、 d e。 捷德的这个图形当中顶点 b e 所在的多面体的表面积是多少? 那么首先咱们就要搞清楚到底经过这几次结之后,含有 b、 e 的 那个多面体到底是一个什么样的图形, 这就非常考察孩子们的空间想象能力。那么我们在做这个题的时候呢,就要一步一步的去给他截,看一看被一个平面截完之后剩下了什么图形, 再被一个平面截完之后剩下了什么样的图形,一点一点的去分析。首先我们先用这个平面 a、 e、 a、 c、 c e 去截这个正方体, 那含有 b 一 的部分其实就是前面这个值三棱柱,我们把它给它重新画出来。接着咱们再来用一个平面去截这个值三棱柱, 那用到的这个平面可以是 a、 e、 b c、 d e 这个平面,所以我们在这个图形当中再把它画出来,那肯定要连一下 a、 e、 b。 然后这个时候咱们就要想一下, 那这个平面跟这个 a、 e、 a、 c、 c、 e 的 这个交线到底在哪里?那么很明显的是这两个平面的交线其实就是 a、 e、 c, 所以 咱们要把 a、 e、 c 给它画出来, 那么截完之后的图形其实就是 a、 e、 b、 c、 c、 e、 b、 e 这个图形,接着咱们再用最后的一个平面 c、 e、 b、 a、 d, e 去截这个图形,那么我们再换一种颜色来看一下截出来以后是什么。 首先我们先来连 c、 e、 b, 我 们接着就要看 c、 e、 b, a, d, e 这个平面跟现在这个红色的这个三角形,它到底的交线在哪里?所以找到交线其实就是找焦点,那很明显这个平面 和 a、 e、 b, c、 d, e 这个平面,它们一定有一个交点,就是这个正方体的中心,也就是 a、 e、 c 的 中点。找到了这个中点之后,我们就可以找到对应的交线,连接 c、 e 和它的中点 o, 然后再连接 b 和 o, 找到这个中心 o 之后,我们来看到底最终这个多面体它由哪些点构成?首先它不能有 a, 因为这一部分直接去掉,也不能有 c, 那 最终剩下的这几个点分别就是 a、 e、 c、 e、 b, 还有这个点 o 以及 b、 e, 那 么我们把这个图形再给它画出来,所以大家来看一下最终剩下的这个多边形就是 o、 a, e、 b、 c, e、 b, e 这个图形是一个六面体,那么这个六面体它各个面的图形形状是什么样的?面积该怎么计算?大家来发现 a、 e、 o、 c、 e 以及 a、 e、 o, b, 还有一个是 c、 e、 o、 b 这三个三角形,它们的两条边分别就是 我们这个正方体的体对角线的一半,那么这个体对角线是根号三,所以它的一半就是二分之根号三,这条边是二分之根号三,这个也是二分之根号三 o、 b 还是二分之根号三。而三条底 a、 e、 a、 c、 e、 b 以及 a e、 b 都是它的面对角线,根号二,所以这三个三角形的面积应该相等。我们来计算一下它的高过这个点 o 做 c, e, a, e 的 垂线垂足一定是它的中点,这一段是二分之根号二,这一段是二分。之根号三,那么这个高就是二分之一,所以这三个三角形的面积和就应该是二分之一,乘以根号二,再乘以二分之一, 再乘以三,等于四分之三倍根号二。接着还有三个三角形,分别是 a、 e、 o, c, e、 o, c, e、 b 以及 a e、 o, b。 这三个三角形都是腰长为一的等腰直角三角形,所以它的面积应该是二分之一,再乘以三,所以最终 小面积就是这个数,再加上二分之三。所以对于这道题目来说,其实还是有一些难度的,我们要能够通过自己的想象和画图,把最终这个六面体给他找到,才能算他最终的表面积。
454高中数学-李钰提分课堂 01:09查看AI文稿AI文稿
01:09查看AI文稿AI文稿孩子立体几何学不好,并不是公式不会,而是题目一变,空间关系就全乱了点线面在脑子里转不起来,后面算的再认真也很容易走偏。高中数学立体几何题型全解,解决的正是这个问题。他不是靠刷题,而是用三 d 动画把空间结构直接呈现出来。 几何题怎么旋转,辅助线为什么要这么画?条件是如何一步步转化的,全部是看得见的过程。 书里的讲法也很克制,不是一上来就堆题,而是先把这一类例题、几何题常见的空间结构和判断思路理清,再用典型题带着走完整解题路径。很多题还会给出不同解法,让孩子明白同一道题,思路是可以切换的。 从公里体系平行垂直到角和距离,结面和动态问题,每一块都是按题型拆开的,配合视频和三 d 动画,帮助孩子真正建立空间感。 如果孩子立体几何提醒经常卡在想不出来,划不明白,这类资料更适合用来把结构一次性理顺,而不是反复试错。资料我放在视频左下角,适不适合看孩子立体几何卡在哪一步?
猜你喜欢
最新视频
- 5.7万人物志bot



