二、无未来函数斐波那契回调线指标代码
粉丝570获赞972
相关视频
 06:36查看AI文稿AI文稿
06:36查看AI文稿AI文稿大家好,有老铁们不太相信,既没有未来数,又没有跨周期去引用的公式的信号怎么会漂移或者说消失,消失后又重现了, 这个呢?还真有,而且的话他真的不存在的,未来函数也没有进行跨周期的调用,但是他的信号呢,是时时刻刻的不见和消失,或者说漂移的现象 非常的明显。好了,我们马上演示给大家看看是不是真的,而且的话也很容易写,也就十来个字母就可以。呃,展现给大家了,我们马上开始,我们打开那个通拿信,在通拿信我们这里可以看到这样一个 复图,未来的信号也会飘的,然后没有化州基调用,一样是会飘的,而且大家经常要注意类似用这样的一些书写的那些公式指标的,大家非常的要谨慎, 但是这个指标呢,他目前呢啥都没有啊,让我们首先呢右键复图修改当前公式, 大家看到他只有一个一啊,一个一是不存在未来的啊,首先呢,这个时候我们把这个什么内容都没有,我们添加一个既没有未来的,但是的话他信号是会飘的,而且是会消失的,消失后还能重现的,是吧,非常 经典的给大家演示这样一种公式的话,大家呢就要谨慎的去使用了,是吧?毕竟我们在真正的那个呃,实战过程中是不存在的,你是啊,参与了他你还 能后悔的是吧?好了,这时候啊,我们直接写一个呃,比如说 w t 啊,或者什么其他的那些,随便你定义这个,然后冒号,冒号以后我们直接用一个 if, 用一个过去的一个时间啊 dat, 然后用一九七零年到一九零零年呢,开始啊,就到现在的那个时间,让我们这时候我们用一个什么样?用一个 l 的,也就是最低价或者收盘价最高价什么都可以随便你写的,后面呢直接你也可以用时间,用数字也可以,也可以直接用 dap 的 dhe, 然后这时候啊我们分号是吧?然后就基本上这里呢就第一行就写结束了,然后我们让他用用一个等号是吧?然后这时候我们再写一个是吧?写一个随便写吧, 然后 w 上 w t o 也行啊,然后直接加个冒号,冒号以后呢我们就用一个 l 上 l 要怎么样?要大等于 w t 的,好啦,就这样子写就可以了,这样写的话,我们看一下他是不是会有信号了,是吧?或者说你也可以大于 w t 或者说是小于 w t 都可以的。 然后我们就用一个等号吧,等于那个 wt, 然后就是创了历史新低啊,类似这样子的是吧?让我们首先呢测试一下好了,测试通过了,它总共呢就是几十来个字母就可以搞定了,让我们测试一下 好了,他这里很明显他是你是一旦他符合要求,他是这里会有信号的啊, 有信号单词的话,现在这个这里的代码,不管你怎么样子修改当前公式,不管你怎么样子去测,这里都是不存在未来的,知道吧?但是的话大家一定要记住, 一般用到了那个按 ef 昨天或者说类似以前的这个时间段,或者特别是用到这个 d a t e 的, 特别是从那个有些是一九七零年到现在的那个时间点,有一些是一九零零年到现在的一个时间点上,但是各个的软件是不一样的,但是他这种的话引用他是不存在的未来函数的, 但是他也没有进行,比如说跨周线啊,跨月线啊,跨年限啊,去调用的问题啊,但是呢,他演示一下,大家看到没有,这下面他也没有呃这个未来的任何的提示啊。如果说你写的有些公式 存在那个资质反转呢?或者其他的很容易就显示出来他有未来函数的。但是我们就前面的一个小视频已经讲过了,用一个快捷键四六的一个三环推演,那就会就会很明显的看得到啊。首先呢,我们呃 就开始演示一下给大家看一下啊,就这里不用其参数,不用管他,直接开始就行了。大家注意下面的一直他都会跟着变的,是吧? 跟着一路过来看,没有看见,刚才那里突然间就有个信号,信号过来,一下子就不见了,知道没有。然后呢时间是在这个位置是吧?信号是在这个位置,但是前面突然间有了,一下下又消失了,这个就是真正的叫做信号有了马上要消失,或者说现在 这个信号就是漂移,他也不地不停的往前飘的,往前移的,是吧?然后大家可以重新看一下,你看这个信号,注意看这里, 你看又有个信号又没有了,是吧?又有个信号没有了,说这种呢,就往往大家要注意了,他是不存在的那个呃函数,未来函数,但是他的信号呢,一下有一下消失,一下漂移,这个就是漂移,这个信号就是会消失,看到没有是吧?看到没有这个 这个是过去的信号的,你要再出来再消失,所以说这个呢就是很简单的一个演示的,而且代码就简单了, 所以说往往呢大家在使用的公式的时候呢,如果说你不知道的他的呃编写的原理啊,或者说呃底层的一些思维逻辑啊,你不明白吧?你用的话就往往就容易吃亏,就在这里面了,是吧?当然大家跟着看我的视频, 至少说在辨别这些公式的好坏上面呢,大家也有了一个新的一个台阶了。好了,大家不信的话,自己就进行这个呃去自己去测试一下的。然后比如说我们修改公式的就很简单了,就是 这两行,两行两行字,而且的话这些你随便调随便改的,呃都是这样的,用到相关的这个 公式,有相关的这个 d、 a、 t、 e 的相关的这个代码的时候,大家就要谨慎,当然他也会经过处理以后,他是 啊,有些是信号是能够不会飘,但是呢正常情况下呢,大家用到类似的 date 这种的话都是要小心一点的。好了,基本上的话我们是不停的学习,不停的进步,然后的话我们下期见,拜拜。
54老帅李华杰 04:50查看AI文稿AI文稿
04:50查看AI文稿AI文稿来了,兄弟们来了,老表们今天随机复盘一单, 照常的打开图标后,先整体看看当前整体行情处于什么阶段, 临时根据这里作分析分割,以红竖线的高点位置看作是下跌的开始,然后数浪区分当前行情处于什么阶段,目前我数做三浪结束回调四浪中四浪的最大范围,匪波纳气回调的零点六一八位置,匪波纳气是根据二浪最高点到三浪的最低点位置, 可能有老表会好奇三浪结束的位置为啥不在这里,或者在未来这里怎么确定三浪结束,因为主包根据区间粗算,三浪内部是七浪小结构。 如果老表还有疑问,请三连在评论区说说。现在详细分析四浪,观察四浪结构,发现三浪最后的下跌和四浪的上升形成了深微结构,这里寻找三浪的底部四浪的起点是否在重要位置上拉升的, 在过往的历史中没看到踩在重要位置上,这里需要注意四浪的向上拉升很强,要假设行情可能转多,假设这段上升是转多的一浪的话,二浪大概在一浪的六十二到七百八十六位置反转, 所以关注六十二到七百八十六位置出现反转信号,现在又发现四浪无法突破前一个高点,也许这也是重要位置, 这里标记反向二浪的最大范围。 走到这里时,我看到 c 浪有小五浪结构,和 a 浪一样, c 浪有可能结束,接下来可能向上震荡低浪或者上升三浪低浪关键区分在红线位置无法突破, 这里根据这根阴线高点做突破点,突破了就确认地或三浪启动, 如果未来行情无法突破红线的,就确认地浪,预想还有一浪,如果行情在上方压力线出现空单信号的也要转空,防止四浪无法突破前高点,这里止损一收盘价在这根强势阳线底部,关注红线收盘在上面水平线还是下水平线, 预想目标位在这根水平线 很惊险,没有收在阳线之下, 突破第一根压力线不再数地浪, 调整止损,防守也是收盘价为主, 这里区间计算三浪是同级别小五浪结构调整止损, 突破了防守止损平仓复盘结束,谢谢观看!
138LaoBiao学交易 03:07查看AI文稿AI文稿
03:07查看AI文稿AI文稿记录,现在是二零二六年一月二十六号晚上十九点四十六分上一个视频谈到了指标型软件,今天进行补充。 无论指标以何种形式展现在我们面前, 所有的指标共分为两大类,一种是含有未来函数的,另一种是不含有未来函数的。也就是在公式指标的公式原代码里边,那原代码是否含有未来函数的问题, 那么他们所呈现出的结果也就分为两种,一种是你看到在低点非常精准,高点也非常精准,这种是含有未来函数的,那么这种指标 他是他的买点和卖点,都是会消失,会自动修正的。 你看似他出现了买点,但是过一会他可能会消失,或者第二天,第三天他有可能消失卖点。同样道理,这就是未来函数的一个弊端, 他是自动修正的,就像低点出现之后,如果出现更低点,那个位置上类似这样的一个情况, 所以未来函数的指标不具备可操作性,原因就在于说他会消失,或者说他会补加,也就是他盘中的时候没有出现买点,那可能盘后的时候他又出现了买点,类似于这样的一个情况。 另一种是不含有未来函数的,不含有未来函数的指标他是不会消失的,但是他的一个问题就是他的买点并非最低点,卖点也并非最高点。 我们可能感觉这种指标也挺好,但是这种指标的话,他有他的好处,也有他的弊端,他的好处是我们可以节省一,节省一些精力, 根据他提供的买点和卖点作为一个参考,那他的短处和缺点是什么呢?就是这种指标在牛市行情当中,或者说单边上涨的市场行情当中, 是不具备很大问题的,也就是说问题不大可以使用。如果在震荡式或单边下跌的行情当中可能就不行了,他会卖点比买点还要低, 而且会经常出现,甚至在震荡式当中频繁的出现,这就是指标看似很神奇, 看似可以参考最后的结果,你发现个他的利弊之后,各种情况的利弊之后,呃,对我们来说参考的意义依然不大。
4一苇渡江 01:09
01:09 43:42查看AI文稿AI文稿
43:42查看AI文稿AI文稿同学们好,又来到小女的数学课,今天我们去学习的是第四章数列四点二点二等差数列的前 n 项和公式。第二课时 学习目标,一、通过等差数列的前 n 项和公式的一个变形应用,体会等差数列的前 n 项和与一元二次函数表达式的一个关联,培养学生的逻辑推理核心素养。 二、通过等差数的前根向后的性质的探求与应用,进一步培养学生的数学运算核心素养。 三、通过等差数的前根向后公式在实际生活中的应用,使学生再一次认识到数学来源于生活,又服务于生活,同时发展学生善于观察生活的优秀品格,培养学生数学建模核心素养。 情景导入小明家的阳光小区就遇到了一个甜蜜的烦恼,共享当初的停放问题。停放区设计不够合理, 高峰期车辆经常摆放混乱,甚至立出到人行道上,既不美观,也存在安全隐患。小明设计了阶梯式的共享单车停放区,第一排放二十辆车位,往后每一排都比前一排多五个车位。 物业采纳小明的设计,需要向小区管委会申请建设基金,必须准确计算出,如果这种新停放区计划修建十五排,那么总共能停放多少辆共享单车呢?这个总数直接关系到预算的审批。 小明设计的这个 j t 式的共享单车停放区,他第一排是放二十辆车了,那就 a 一 等于二十,要他说往后每一排都比前一排多五个车位,那么这个是符合我们等差数列的定义。 五个车位,那这个五就是我们的公差 d 等于五了, 他说现在是呃计划修建十五排,那么总共能停放多少辆共享单车?那就是呃前五十项的和等于多少? 那知道了首项和公差,那么我们利用公式 s n, 它是等于 a n a 一 加上二分之 n 乘以 n 减一 的差乘低,那么带进来 s 十五,那就等于十五, a 一 加上二分之十五乘十四再乘低 啊,那我们带进来就可以得到 s 十五十五, a 一 就是十五乘二十,加上这个这个二和十四可以约到一个七的,那就十五乘 七公啊,公差 d 四五,那把这个数算出来,就能够算出总共有多少辆共享单车了啊! 这就需要用到本节课要学习的等差数列前项和公式的应用, 建立等差数列模型,解决实际问题。解析,设阶梯式停车,从第一排到第十五排,各排的停停车位数依次排成一列,构成了我们这个数列 n, 其前十五项和为 s 五。 那么根据题,我们可以得到数列 n, 它是一个公差为五,首项为二十的一个等差数列, 那根据等差税前 n 项和公式,那我们就会求助 s 十五,因此修建十五排总共能停放八百二十五辆共享单车。新知应用 例题七,已知一个等差税 a n, 前十项的和是三百一十,前二十项的和是一千二百二十。那么有这些条件能确定这些等差税的首项和公差吗? 那它已经告诉我们这个数列是等差数列,那这个首项和公差我们可以设一下啊。设这个等差数列的首项为 a e, 公差为 d, 那 么由题可得,前十项的和是三百一十,那么 s 十就等于三百一十, 前二十项的和是一千二百二十,那么 s 二十就等于一千二百二十, 那我们带进来就十。 a 一 加上二分之十乘九乘 d 等于三百一十, 那二十 a 一 加上二分之十乘十九乘公差 d 等于一千二百二十,那么列出来关于首项和公差的一个方程处,那么可以把这个首项和公差取出来即可,那么就可以由这些条件能确定这个等差数的首项和公差。 在例题七条件下计算 s 三十, 在例题七的条件下,我们算出它的首项 a 一 是等于四的公差 d 四等于六的除算出 s 三十,它是等于三十 a 一 加上二分之三十乘二十九,再乘 d, 那 么等于三十乘四,加上啊 十五乘二十九再乘六,那么从而算出我们 s 三十 等于二七三零。好,继续并判断 s 十 s 二十减 s 十,逗号, s 三十减 s 二十,能否为等差数,那我们把 s 十求出来, s 十的话,刚才已经告诉我们是三幺零 s 二十,它是一千二百二十, 那么所以的话呢, s 十是不变的,那么 s 二十减去 s 十的换到半,那就是一二二零减去三幺零,那就等于九幺零了, 那么 s 三十减去 s 二十,那就等于二七三零减去一二二零,那就是一五一零了。 他问我们是否为一个等差式列,那就是,呃,每一项跟它前项相减,你看下这个 s 二十减去 s 十,再减 s 十, 你看减出来的就是六百,那同样道理,我们这个 s 三十减去 s 二十再减去 s 二十减去 s 十,那么这个是一五一零,减去九幺零,它也是等于六百。那么啊,每一项跟前一项相减,减出来是同一个常数, 那么这个常数是公差数,这里是取等号的,那说明它是形成一个等差数列的啊。 一般的 s m、 s 二 m, s 三 m 分 别为等差数 n 的 前 m 向前二 m 向前三 m 的 和,则我们就可以得到 s m 逗号 s 二 m 减 s m 逗号 s 三 m 减去 s 二 m, 就 乘等差数列。 例题八,某校新进一个报告厅,要求容纳八百个座位,总共是八百座位。报告厅共有二十排座位, 一说这二十排个座位总共坐八百个座位。从第二排起,后一排比前一排多两个座位。问,第一排应安排多少个座位, 后一排比前一排多两个座位,那此时这一个有等差数列的定义,那么这里从第一排到第二十排,那此时这二十排座位形成了一个等差数的 a n。 问,我们第一排应安排多少个座位?那由这里可得。后一排比前一排多两个座位,它是形成一个等差数,那么这个公差 d 是 等于二的, 总共有二十排,那这二十排呢?可以容纳八百个座位,那么说明 s 二十它是等于八百的。问,我们第一排应安排多少个座位?那么设第一排应安排我们首个座位,就设为 a 一 嘛,就可以了。那么根据等差数前项和公式,我们就可得 s 二十 就等于二十 a 一 加上二分之二十乘十九,再乘公差 d, d 是 二,那么这个总共是八百啊!由这个关于 a e 的 一个方程解出 a e 即可。 等差向量前 n 项和的应用问题。从上述引力情景和力坝的探求中,你能总结下建立向量模型解决实际问题的基本步骤。实际问题,数学切模向量问题, 用一个等差向量表示实际问题中乘等差关系变化的量。 树立问题,以知未知化,建立关于未知量的方程。方程思想,求解未知量,解方程,求未知量未知量回归问题。 第一章丘介算经是我国古代内容较为丰富的数学名著,书中有这样的一个问题,经有吕尚之日以月之久痞 三尺,问日异几何其意思为,有一个女子织布,每天比前一天多织相同量的布, 每一天比前一天多织相同量的布,一天织五尺,一个月按三十天来降,总共织三百九十尺。问每天多织多少布?已知一匹等于四丈,一丈等于十尺,是计算该女子每天多织的布为多少尺, 每天比前一天多支相同的量,那么有这个以及根据等差数的定义,那我们得到它,这个是形成一个等差数,从第一天到第三十天形成一个等差数, 那么从这里的话呢?啊,我们啊,每一天比前一天多支相同的量,这个相同量我们即为公差低, 那么第一天是积五尺, a 一 等于五,那么一个月共织三百九十次,那么 s 三十就等于三百九十。问每天多织多少布, 就是问公差是多少,每天比前一天多支相同量,这个相同量的步就是公差低了。好,那么设为啊,设每天多支 d 部啊, a 部, d 部, s 部,那么由这个形成一个等差数列, 那么 s 三十,它是等于三十, a 一 加上二分之三十乘二十九,再乘公差 d, 那么列出啊,我们把 a 一 等于五带进来,就可以列出啊,这个公差,关于公差 d 的 一个方程,解出公差 d, 这个公差 d 解出来就是每天多只的布量了。 例九,已知等差税 a n 的 前 n 项和为 s n, 若 a e 等于十,公差低等于负二,则 s n 是 否存在最大值?若存在,求 s n 的 最大值,即取得最大值时 n 的 值若不存在,请说明理由。 我们看一下这个等差率,首项是 a 一 等于十的公差 d 是 等于负二的,那么从单调性来看的话呢,它是一个单调递减数列,首项为十,那它是一个递减数列, 那很明显它前面的项都是正的,那从后面的。像是当的 n 的 值越来越大的时候,它的值是越来越小的, 那前 n 项和 s n 前 n 项和,那就是取得最大值,那就是所有正数相加,或者是所有非负数相加,那么取得就是它的最大值了。 那这个点的话呢,是从我们单调性来思考的。好,那这样的话,我们看一下这个等差税前 n 项和,我们知道是 a 一 等于十,公差 d 等于二的,那如果我们从单调性来考虑的话,那么首先我们可以求出这个等差税的呃,通项公式, a n, 它是等于 a 一 加上 n 减一的差,乘 d 带进来十加上 n 减一,乘以负二,那就等于负二, n 加十二,这是它的一个通项公式。 那求 s n 的 最大值,那我们看一下,我们令这个 a n 大 于零时, 既负二 n 加十二,代数 n 小 于六, 令 a n 等于零时,那么求出这个 n 是 等于六的。令 a n 小 于零时,求出这个 n 是 大于六的,那么从这里可以分析出来,当 n 小 于六或等于六时,那么此时 a n 前六项都是一个非负数, 从第六项开始,那么此时 n 是 n 是, 它是一个负数。来了,我要满足前 n 项和是最大值,那是把那些非负数加起来就可以了。 那从这里我们可以知道了,第六项它是 n 是 等于零的,所以它会当 n 等于五,或者是当 n 等于六的时候,那么此时前 s n 是 取得最大值的, 那我们带个 s 五或者 s 六带进来,那么所以 s 五等于啊六 a 一 加上二分之六乘以五,再乘公差 d, 那 么六 a 一 是十,加上啊,我们约一个,那就十五乘负二, 那么六十减去三十,算出来是三十,那么此时当 n 等于五或等于六的时候,取得最大值,那最大值为三十。此时我们是通过这个啊等差数的单调性来求的, 那么我们还没有其他方法呢,它不是求 sn 的 一个最大值吗?那我们首先先将其 n 项和先求出来, 那知道首项 a 等于是公差 d 等于负二,那么 s n, 那 就等于 n a 一 加上二分之 n 乘以 n 减一乘公差 d, 那 带进来啊,十 n 加上二分之 n 乘 n 减一乘负二,那得到是啊,负 n 方,嗯,加十一 n, 我们算出来,它是一个关于 n 的 一个二次函数,而且开头方向是向下的,它的方向向下的话呢,那此时它有一个最大值了,那么把它进行一个配方,负的 n 方减十一, n 加上二分之十一的平方, 好,减去四分之一百二十一。好,那我们去掉括号,得到是负 n 减去二分之十一的平方,加上四分之一百二十一。 我们从这里可以知道,当 n 等于二分之十一的时候,那么此时 s n 是 取的最小值的,但是呢,我们这个 n 是 属于正整数的,因为我们的 n 是 属于正整数的, 所以我们靠近二分之十一的那一个正整数看是谁。那么二分之十一是五点五,那么靠近五点五的正整数,那有五和六,所以当 n 等于五 或 n 等于六十,那么此时 s n 取得最大值,那么 s 五就等于 s 六,就等于我们把它带进来。我们带一个 s 六,那它这里是二分之十二。 减去二分之一就二分之一的平方,那就负的负的四分之一加上四分之一百二十一,那算出来也是三十,那只是通过是二次函数的角度求出它的前 n 项和的最大值。 方法总结等差数的前 n 项和的应用在等差数 n n 中,当 a 大 于零小于零时, 其实前 n 项和有最大值,那使得前 n 项取得最值的 n, 可由不等式组 a n 大 于等于零,或者是 n 加一小于等于零确定。 当 a 一 小于零时, d 大 于零时,前 n 项和有最小值,使得 s n 取得最值的 n, 可由不等式组 a n 小 于等于零, n 加一大于等于零来确定。 二、前 n 项和 s n 等于二分之 d, n 方加上 a 一, 减去二分之 d 的 差,乘 n 二公差 d 不 等于零的。二次函数的角度中,当公差 d 大 于零时,那么前 n 项有最小值。当公差 d 小 于零时,前 n 项有最大值。 当 n 取最接近对称轴的正整数时, s n 取得最值。等差式的全项和公式的一个函数特征,探求已知式 n 的 全项和为 s, n 等于 p, n 方加 q, n 加 r, 其中 p q r 为常数, 且 p 不 等于零。求向量 a n 的 通项公式,并说说你有什么发现。那么已知向量的前 n 项和 s n 如何求出 a n 的 通项公式呢?那此处这里有一个公式法,我们的 a n, 它是等于 s 一, 当 n 等于一的时候,当 n 大 于等于二的时候呢,那就得到是 s n 减去 s, n 减一。好,那我们一起来看看。 当 n 等于一时,那此时 a 一 等于 s, 一 就等于 p 加 q 加 r, 当 n 大 于等于二十,那么 s n 减一等于 p 乘以 n 减一的平方加上 q 乘以 n 减一加 r, 那 带进来 n 方减二, n 加一加上 q, n 减 q 加 r, p, n 方减二, p, n 加 p 加 q, n 减 q 加 r。 好,所以 a n 等于 s, n 减去 s, n 减一就等于 p, n 方加上 q, n 加啊,减去减去这一对 偏方减二 p n 啊,就不会写了。那等于好,减去它之后,我们看一下啊,偏方加上 q, n 加上啊,减去它,那去掉括号之后反而相反。偏方加上二 p, n 减去 p 减去 q, n 加 q 减 r 啊,我们看能不能约到偏方和偏方约掉啊,减 r 和减 r 也约掉,那这个是啊,加 q n 和减 q, n 也约掉了,那么留下来是 二 p n 减 p 加 q 减 n 等于一时,那只是 a e 把它代值得到是二 p 减 p 就 p 加 q 了。 好,那所以怎么去下载呢?我们看一下,你看这里 a 加 p, 呃,这个手像是 p 加 q, 这里的手像是 p 加 q 加 r 的, 那所以当 r 等于零时,那么这个首项 a 和这个首项就满足了嘛?满足上式的时候呢?此时这个 a 呢?通向公式就等于二 p n 减 p 加 q, 当 r 不 等于零时呢?那此时 a n 就 分分段函数均为斜了,那一个是 p 加 q 加 r 了, n 等于一的时候,那么 n 大 于等于二的时候,那就是二 p, n 减 p 加 q 了, 我们就分成了。当 r 等于零的时候呢,那此时这个通项公式是满足的,那此时它是一个呃,为等差数位,公差为二 p, 首项为 p 加 q 的。 当 r 不 等于零的时候呢?此时首项为 p 加 q 加 r, 其实不满足这个式子, 那此时从第二项起,才为一个等差数列已知数 a 的 前一项和 s, n 等于偏方加 q, n 加 r, 当 r 等于零时,此时数 n 为等差数,且首项为 a 等于 p 加 q, 公差为二 p, 当 r 不 等于零时,此时 a 为。从第二项起才是一个等差数,且公差为二 p 等差税 a 呢?前向好 s, n 等价于 s, n 等于 a, n 方加 b n, 其中 a 等于二分之一 d, b 等于 a 减二分之一 d, 这里是互推,是一个冲量条件。 另二,在等差税 a 中, a 二加 a, 三等于负三十八, a 十二等于零,求 s n 的 最小值以及相对应的 n 的 值, 那求前项和的最小值的话呢?这个等差数的话呢,我们有两种思路,一种是从单调性,一种是从二次函数的最大值和最小值去出发。 那首先他不是知道 a 二和 a 三加起来等于负三十八吗? a 十二等于零,那由这两个信息的话呢,我们就可以求出首项和公差,那么设这个等差数的公差为 a, 首项为 d, 那么得到是 a 一 加 d 加上 a 一 加上二 d 就 等于负三十八,那么 a 十,而是 a 一 加上十一, d 就 等于零, 那么由这里我们就会解出我们的首项和公差,我们看一下这里,好,那这个式子一式,那就是二 a 一 加上三 d 等于负三十八,那对二式我们乘一个二,那二 a 一 加上 二十二, d 等于零,要两式相减二十二减三,那就是等于十九十九 d 啊,零减负三十八,就零加三等于三十八,求求公差 d 四等于二,那公差 d 四等于二代进来这里 a 一 加上二十二等于零,求求首项 a 一 等于负二十二, 那此时我们可以通过一个单调性,它是单调递增的,并且呢首项是为负二十二, 上面前面前面的数是负的,那随着 n 的 越来越大,那么这个最后的值是越来越大的,那它是一个递增函数嘛?所以大家想要前 n 项和 想要前 n 项和的最小值的话,那就是前面那些啊,非正数相加,非正数相加,那得到是前 n 项和的值是最小的, 那我们首先可以从单调性来看,我们看一下,如果 a n 它是等于 a 一 加上 n 减一乘 d, 那 么带进来 a 一 是负二十二,加上啊,这个乘二的话, n 减一乘二 等于二 n 啊,减二减二十四,对吧?那首先能看一下,那么 a n 如果是小于零 二, n 减二十四,小于零的话,那我们求出 n 四小于十二,当 a n 等于零时,求出 n 四等于十二。当 a n 大 于零时,求出 n 四大于十二。那从这里可以分析出来,当 n 小 于十二时, 那么 a n 都是小于零,当 n 等于十二的时,它是等于零,那说明前十二项跟前十一项的最小值是一样的, 因为第十二项是为零嘛。所以当 n 等于十一或者是十二时,那么前 n 项和取得最小值,那么把 s 十二算出来, s 十二就等于 s 十一了, 那么十二 a 一 加上二分之十二乘十一再乘以,那么前十二项的和就可以求出来了啊。那么一种方法,单调性 将我们这个首项和公差求出来之后,那么 a n 等于这个。当 a n 小 于等于零,当 a n 加一大于等于零时,那求出我们 n 四大于等于十一,小于等于十二。 所以当 n 等于十一或者 n 等于十二时,取得最小值,那就想把它代入,求出负一百三十二。这种方法就是啊,配方法就是从二次函数的角度去除吧。重要题型 题型一偏段和 s m 等于二十,前三 n 下的和为 s 三 m 等于九十, 则它的前二 n 项和 s 二 n 为多少?在等差数列当中,我们有一个性质,我们知道 s m 逗号 s 二 m 减去 s m 和 s 三 m 减去 s 二 m, 这三个数是乘等差数列的, 所以我们就有 s 二 m 减去 s m, 再减 s m 就 等于 s 三 m 减去 s 二 m 再减去 s 二 m 减去 s m, 那这个话我们把它带进来, s m 是 等于二十的, s 三 m 等于九十,那么 s m 不 变啊,这个 s m s m 的 话,等于二十就减四十了,就等于九十,减去 s 二 m, 减去 s m, 加上 s m。 好,那么这里带进来这个啊, s 二 m 减四十就等于九十啊,减去两个 s 二 m, 再加上二十,那把这个移过来就是三个 s 二 m 就 等于九十,加十就一百一十,那把四十移过来就一百五十了,所以 s 二 m 就 等于五十。答案是选 cat 题型二和比求向比例题。等差数 n b n 的 前缘相和分别为 s n, t n。 已知 s n 比上 t n 等于二 n 加三,比上 n 加四,则 a 六比上 b 六的值为多少。 只有我们可以清楚地知道,等差数的前 n 相和它对应的就是我们的二次函数,但是它这个比值不是二次函数,所以的话呢,我们可以呃把它转化成有关二次函数的,那此时我们可以念我们 s n, 它是呃乘以个 k n 二 n 加三,那此时就可以得到二 k n 方加上三 k n, 同理 p n 的 话,也是乘个 k n 就 得到是 n 加四就等于啊,就是 k n 方加上四 k n, 那 它求 a 六和 b 六,那 a 六又可以写成什么呢?那么在 a 六当中,我们就可以得到是 s 六,减去 s 五, 那么 sn 等于这个,那么把 s 六带进来, s 六的六的平方就三十六,三十六再乘以二,那就是七十二 k 加上啊,这个六啊,十八 k, 这个是 s 六的,再减去 s 五, s 五五的平方是二十五。二十五乘到五十 k 啊,再加上十五 k, 那 么把它算出来,看一下算出来是多少啊?首先这里是呃,七加一就八九十 k 减去六十五 k, 那 算出来是二十五 k, 那同样我们这个 b 六个 b 六,它是等于 t 六减去 t 五,那么 t 六带进来啊,三十六 k 加上四六,二十四, 二十四 k 减去 t 五,二十五 k 加上二十 k, 好, 那么得到是,那么这个是得到,是啊,六十 k 减去啊四十五 k, 得到是十五 k, 所以 a 六比上 b 六,就等于二十五 k 比上十五 k, 那 约掉 k, 再约一个五,等于三分之五,所以它的比值是三分之五。 那还没有其他的一个方法呢?这个 a 六的话呢,我们知道是二六十二,二六十二的话呢,那我们知道 a 一 加上 a 十一等于 a 十二的, 所以的话呢,那我们就选择是前十一项和,前十一项和,那就是等于二分之十一乘以 a 一 加上 a 十一,就等于,那么 s 十一的话,首先 a 一 加 a 十一, 就等于啊,十一乘以 a 一 加十一,就是两个 a 六除以啊,那等于十一 a 六, 而 t 十一的话呢,这个 b 六就是 t 十一嘛,那 t 十一也是二分之十一乘以 b 一 加上 b 十一,那就等于十一 b 六。所以我们这里的 a 六比上 b 六, 就是两边同时乘以十一 a 六十一 b 六,而十一 b 六就是等于 s 十一 十一 b 六就是等于 t 十一,那带进来,这个 n 是 等于十一,那二乘十一加三除以十一加四,那带进来,那么这里是二十二,加上就二十五,那这里是十五,那算出来还是三分之五。 题型,三等差式前 n 项和的单调性与对称性问题。 例题,在等差速 n 中, s n 是 其前 n 项和,且 s 二零一六等于 s 二零二一,则 s k 等于二零二一四,则正整数 k 为多少? 其实我们清楚一个知道前 n 项和等差速的前 n 项和,它是关于 n 的 一个二次函数,那关于 n 的 一个二次函数的话呢?那它就是有一个 假设,他开口方向下的话,那就有个对称轴,对称轴,那对称轴的话呢?比如这个点和对称这个点是一样的,那这个对称轴是作为中点的,那假设这里是这个,是啊,这个点对呢?是横坐标是二零一六,那么前二零一六, 那对应这个点就是二零二一,逗号 s 二零二一了,对吧?那同样道理,二零一四,二零一四对应这个点,那么二零一四,那逗号 s 二零一四,那么对应的是这个点,是哪一个点呢?是不是对应是哪一个点? 那那这样的话呢?很明显,那这个对称轴它是在中间的,那此时我们就可以知道,二零一六加上二零二一啊,除以二就等于我们的 k 加上二零一四,除以二, 那我们把二约掉的话,那词从而就求出我们的 k, 那 就所以 k 加上二零一六加上二零二一了, 那么 k 四等于移过来,就是这个二零一六减二零一四就二了,那就二零二一加二就等于二零二三,所以答案是选到 题型四,等差数 a n, 求数 a n 绝对值的前 n 项和问题例题,已知数 a n 的 前 n 项和为 s n 等于二 n 方减二十六 n, 那 么从这里我们可以知道它是一个等差数列 一求向量 n 的 通项公式,判断这个向量是否是等差向量,并说明理由。那么已知 sn, 那 求 n 的 通项公式,那我们都是用公式法。 an 它是等于, 首先是 s 一 的时候, n 等于一,当 n 大 于等于二时,那此时 an 它是等于 sn 减去 sn 减 e, 所以我们写成的是 g d。 问,当 n 等于一时,那就是 a 一 四等于 s, 一 就等于二。次来二减二十六,等于负二十四。 当 n 大 于等于二十,那我们就用公式。那先求 s, n 减一, s 二乘以 n 减一,到平方减去二十六,乘以 n 减一,好带进来, n 方 减二, n 加一减二十六, n 加二十六, 那就等于二。 n 方减四, n 加二减二十六, n 加二十六,那就是等于二。 n 方减去三十, n 加上二十八, 所以 a, n 等于 s, n 减去 s, n 减一, s, n 是 二, n 方减去二十六, n 减去它 好,那么最终算出来是四, n 减二十八, 当且 n 等于一时,求出这个 a 一 把它带进来,也是负二十四,这里 a 一 等于负二十四,这里的 a 也是等于负二十四,那说明这个通项公式它从第一项开始也是满足的。所以下载了 a, n 等于四, n 减二十八, a 算出来是四, n 减二十八的话,我要证啊,就是这个通项公式了。那这个由这个通项公式我们一眼可以看出来,它是一个等差数,那怎么去证明它的等差数呢?那我们把它的前一项求出来,所以四 a, n 减一等于四,乘以 n 减一,减二十八,那就是等于四, n 减三十二,那么用每项跟它前一项相减, 那么这个减这个,那就四 n 减二十八,减四, n 加三十二,那减出来等于正四,那么这个四那就是作为它的公差,那么首项首项 a e 是 负二十四, 所以它是一个等差率,它是以啊负二十四以为首项以四为公差的一个等差数列 a n 的 绝对值,前 n 项和为 t n, 问我们第几项的和式等于一零八了, 那我们用刚才的单调性,我们知道这个呃呃 是一个单调递增数里首项是一个负数的,那我们来了解一下,当 a n 这个是小于零时,那此时得到是四 n 减二十八小于零,得到 n 小 于七 a 一 l a 三 a 四 a 五 a 六这六项的话呢,它都是小于零的, 那么 a n 等于零的话,求出 n 是 等于七的,第七项的话,则 a n 是 等于零的。那么 n 大 于七的时候呢?此时 a n 是 大于零的, 当我们这个 n 小 于等于七时,那此时这个 t n 它是等于 a 一 的绝对值,加上 a 二的绝对值,加上 a 三的绝对值, 再加上 a 四的绝对值,一直加到 a n 的 绝对值,那又等于什么?因为 n 四小于等于七的。 我们知道啊, n 小 于等于七的话呢,那么前七项它每一项都是一个啊非啊非正数,那这样一个非正数的话呢,去掉绝对值符号,那就是它的相反数,那提个符号出来,就知道是 a 一 加上 a 二,一直加到 a n 好,那等于,那这个是前 n 项和前面一个符号,那么前 n 项已经告诉我们了,它是等于负的。二 n 方减二十六 n, 那 么这个结果算出来等于负二 n 方加二十六 n, 其实这个 n 是 小于等于七的,那我们看一下,当 n 大 于七的时候呢,其实 t n 它是等于 a 的 绝对值,加上 a 二的绝对值,一直加到,先加到 a 七的绝对值,再加到 a 八的绝对值,一直加到 a n 的 绝对值, 那等于什么呢?因为从刚才分析的话呢, n 小 于七的时候,它是一个非正数,所以去掉绝对值符号呢?那就负的 a 一 一直加到 a 七 好,后面从第七项开始,那就 a 八开始,它是一个正数,那得到。是啊, a 八一直加到 a n, 好,那负的,那么前面这个 a 加 a 七,那不就是我们 a n 的 前七项和吗?那就 s 七加上后面 a 八加到 a n 的 话,那它就是用前 n 项和减去我们前七项, 就得到是 a 八加到 a n 了,那么它整理得到是 s n 减去二 s 七好, s n 就是 等于这个了。二 n 方 减去二十六 n 减去二 s 七, s 七的话,把七这里带进来,就是二乘以七的平方四十九减去二十六乘七,那把这个结果算出来即可,那最终算出来,我们看一下,那就是二 n 方 减去二十六 n 加上一六八, 好,那么分两类。讨论完之后,他说 t n 等于一六八,那么分成 d 类。当 n 小 于等于七的时候,那么这里负二 n 方加上二十六 n 等于一零八,把这个 n 解出来。同样道理,我们当 n 大 于七的时候,那么指出二 n 方减去二十六 n 加上一六八等于一零八,那我们也将这个 n 解出来,那我们解出这个 n, 首先需要注意的是,第一个 n 是 属于正整数,第二的话呢,这一个是指等于一零八时,求出这个 n 的 范围是在 n 小 于等于七的, 而这个 n 解出来的正整数范围呢?是 n 是 要大于七的才可以,要我们一起来看看。 你看,从这里我们分析的话啊, n 小 于等于七的时候,那么其实前七项都是一个非啊,非正数都是一个负数,那么去掉绝对值就是它的相反数,那就是负的开始 n, 而 n 从第七项起都是正数了啊,那分成两个, 此时我们可以念这个等于一。零八解出 n 等于十或等于三,但是这个 n 等于三,为什么舍去呢?因为这个式子它是在第八项开始才满足的,所以解出 n 等于十。 方法总结,等差数 n 求数 n 的 绝对值的前 n 项和问题,求数 n 的 绝对值的前 n 项和的绝对值之和 有绝对值的意义。我们必须分清这个数列哪一些项是负数,哪一些项是非负数,然后再分段求前项各项的绝对值之和。 柯南小杰等差向量前 n 项和的性质与应用等差向量前 n 项和的应用等差向量前 n 项和的句子问题,通向公式式学, a n 大 于等于零, a n 加一小于等于零,或者 a n 小 于等于零, a n 加一大于等于零。二次函数视觉, s n 等于二分之一 d, n 方加上 a 一 减去二分之一 d 的 差乘 n 等差数减 n 向和的性质片段和的性质, s m s 二 n 减 s, n 减 s 三 n 减 s 二也乘等差数乘为 n 方 d 速列 s, n 比上 n 的 性质,速列 n 是 公差为 d 的 公等差税,则速列 s, n 比上 n 也是等差税,且公差为二分之一 d 前 n 下核的比值。两个等差税 n、 b, n 的 前 n 下核分别为 s, n、 t n, 则 n 比上 b n 等于 s 二 n 减一,比上 t 二 n 减一。含绝对值的求和问题。
53侠女的数学课 00:10
00:10 10:32
10:32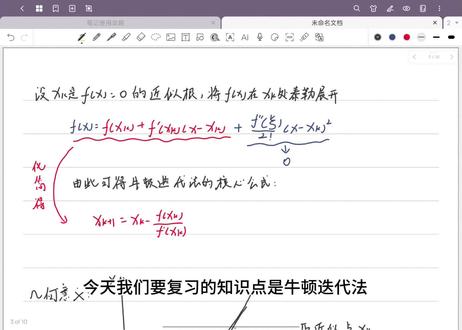 05:04查看AI文稿AI文稿
05:04查看AI文稿AI文稿今天我们要复习的知识点是牛顿迭代法。牛顿迭代法的基本思想就是将非限性方成限性化。我们对所求函数进行泰勒展开,取一项为零,再化简成关于 x k 的 式子,于是就得到了牛顿迭代法的迭代公式,再让我们看看它的几何意义。 x 星是函数的根,我们取一个近四根 x k 过曲线 y 等于 f x 上横坐标为 x k 的 点的引切线,并将该切线与 x 轴交点的横坐标 x k 加一,作为 x 的 新的近四值 不断迭代,可见函数根的近四节不断逼近函数的根。由于这种几何背景,牛顿迭代法也称切线法, 再让我们看看它的收敛性。在单根情况下, five x 星的一次岛等于零,而 five x 星的二次岛不等于零。因此牛顿法在单根处具有二阶收敛性,这意味着它的误差会以平方的速度迅速减小,收敛速度非常快。 接下来我们直接来实操,根据迭代公式求解, 将 x 零等于一点五,带入公式,得到 x e 的 值,再将 x e 的 值带入,得到 x 二、依次叠代。 当我们稍微变动一下,将数值改为零点六,会发现误差特别大,远偏于 x 星。 根据这个现象以及前面讲过的收敛性,可以得到牛顿迭代法的一个优点和缺点,优点是收敛速度快,而缺点就是对数值很敏感。为了改进这个方法,书中给出了简化牛顿法和牛顿下山法。我们先来看简化牛顿法, 先算出 x 零的导数值,并在此后的迭代中保持不变, 然后跟牛顿迭代法一样,将 x 零带入求 x 一, 然后依次迭代。 然后我们来介绍一下牛顿下山法,这是牛顿法与下山法的结合。 下山法是引入下山因子,将布长减小,缩小每一步的更新幅度,避免偏离。首先我们就是要计算出下山因子,使迭代都满足下降条件。如果不满足 f x k 加一小于 f x k, 就 将下 山因子小于三十二分之一时,满足了下山条件。于是我们取那的为三十二分之一, 进入第二次迭代后,看是否依旧满足下山条件。 发现依旧满足下山条件后,就按照牛顿迭代法依次迭代。
4椰丝 01:49查看AI文稿AI文稿
01:49查看AI文稿AI文稿你知道吗?医学的底层是生理学,生理学的底层是化学,化学的底层是物理,而物理的终极底层竟是数学!数学没有更低的逻辑支撑,它是所有科学的根基,甚至可以说万物皆数学。 你看到的向日葵,真的只是一朵寻常的花吗?仔细观察它种子的排列螺旋每圈数量严格遵循十三、二十一、三十四这样的数字规律。这组被称为斐波纳契数列的数值。你以为蒲公英的形态是造物主 随性挥洒的浪漫,实际上,它飘散的弧线同样严格遵循斐波纳奇螺旋这种结构能在有限空间内最大化种子数量,也保障了它们能被风有效传播。这并非大自然的偶然巧合,而是宇宙早已写就的通用密码,在看不见的角落也默默印证。而许多人一生都认为自己不擅长数学, 往往是因为从没人告诉他们,数学的目标并非刷题得分,而是人类探索世界最浪漫的一场远征。读完这本书,我最大的感受是学生时代所有关于数学的为什么?终于有人为我一一透彻解答,为什么一次函数的图像是直线, 而二次函数画出来却是抛物线?函数究竟是什么?它和方程有什么关系?微积分听起来高深莫测,究竟能解决什么问题?书中建筑生活中有趣的实力,将一百多个抽象的数学核心概念以可式化方式呈现,连小学生也能轻松看懂。例如,用包饺子的过程讲解比例关系, 用灯泡的明暗讲清二净制与实净制,用棋盘格把指数增长的原理彻底讲透,读完才真正明白,数学从来不是零散的知识点, 而是一套逻辑严密、环环相扣的思维体系。读懂这本书,就等于为初高中数学打下了扎实的基础。诚挚推荐给装学生、各位家长,以及所有希望在碎片时间里重新拾回数学魅力的人!
0东方之书 00:10
00:10
猜你喜欢
最新视频
- 8981超能信号







