5年级几何训练100题
同学们大家好,今天呢,我们来看一道五年级的必考知识点,就是我们的一个哎,几何图形组合图形这个章节的,那我们今天呢要做的这个题呢,是一道附加题,拔高题比较难,同学们,我们一起来看一下,已知正方形的面积呢,是九十六平方厘米。 啊,这个正方形啊,同学们看这里有一幅图,它是一个正方形,它的面积呢是九十六平方厘米。好,要求阴影部分的面积,给的条件很少,那我们求这里的阴影部分的面积,还知道这个点呢,是我们的一个 这条线段的中点,那这里呢,我把点呢给同学们标出来,这里就是 a, b, c, d 相当于呢,我们这里的中点呢,我们给它标成 e, e 呢就是 bc 的 一个 终点。那题目的条件没有了,题目的条件很少,一个是面积,一个是终点。那怎么去做这道题呢?那我们肯定要从这里的一个终点去入手,因为给的九十六呢,它是整个 正方形的面积啊,很难入手,那这里的终点我们可以入手啊,那看到终点我们可以想到什么呢?哎,同学们看, 我们在我们这个正方形里面,这个阴影部分呢,它是一个三角形。好,我们这里把它标成 o, 就是 obe 呢,它是一个三角形,由于这的意思,中点我们可以想着什么呢?想到去连接一条辅助线 o, c, 那为什么要去连接这一条呢?由于 e 是 b, c 的 中点,那我连接之后呢?同学们看,同学们观察这个 o, b, e 这个三角形和 o, e, c 这个三角形,它们有什么特点啊?哎,它们俩是不等底等高的呀, 它们的高都是这一条,它们的底呢是 b、 e 和 e、 c, 由于 e 是 中点, b、 e 等于 e、 c, 哎,所以这两个三角形它是它的面积呢,是 完全一样的,如果这里是一份的话呢,那我们这里是不是也应该是一份啊?好,现在我们再来看,在我们正方形里面呢,我们的 b、 d 呢是对角线, 那对角线这个 b、 d 呢?它是不是就是我们这个正方形的一条轴对称呐,它相当于我们这个 a、 b、 c、 d 呢,它就是一个对称轴图形,我的 b、 d 呢,它就是一条轴对称,那这个时候我们沿着 b、 d 把这个正方形给它对折过来。哎,就是把这个 a 点和 c 点 重合,那同学们就会发现,我这个三角形 a、 b、 o 和我们的 o、 b、 c 是 怎么样的呀?是不它会重合呀?是不完全一样,那这里一共是两份, 那我们这里是不是也应该是两份啊?那这个时候我们再观察,我们就得到了一个三角形的分数,也就是 a、 b、 e, 是 不是一共是三份?那得到 a、 b、 e 有 什么用呢?同学们看,同学们观察一下,这个 a、 b、 e 跟我们这个正方形它有什么关系啊? 哎,因为这里的 e 呢是中点,我们可以这样去画一条辅助线,可以把它分成两个长方形,那同学们就会观察到,我这个 a、 b、 e 呢,其实就是我正方形的 怎么样呢?是不是四分之一,也就是除以四,是不是对应着三份啊?所以我们就哎有思路了,用我们的第一步,用我们的九十六呢去除以四,算出我们 a、 b、 e 的 一个面积。好,这里呢同学们算一下等于多少呢?等于二十四 平方厘米,那二十四平方厘米对应的是 abc, 这里一共是三份,我们的阴影部分呢是对应的一份,所以呢我们再用二十四呢去除以我们这里的二加一的和再乘个一就可以了。 好,那这里呢,我们算出来就等于一个八平方厘米,哎,我们阴影部分的面积就得出来了,那这里呢,我们涉及到的知识点呢就比较难,首先第一个我们要连接辅助线 o, c, 那 怎么去连接呢?因为这里的意思终点连接 o、 c 之后呢,是两个等底等高的一个三角形,那我们就知道这里是一份,这里呢也是一份,这是第一个思路,第二的一个思路呢, b、 d 呢是对角线,我们把正方形沿着对角线折叠之后呢,左右两边是完全一样的。好,所以呢,我们这个三角形 a, b、 o 和 o、 bc 呢,它是可以完全重合的,那对应着这里就是 两份儿,那整个 a、 b、 e 呢就是三份儿。那再根据我们刚刚写的步骤,哎,我们这个题呢就得出来结论了。
粉丝2083获赞8632
相关视频
 02:21查看AI文稿AI文稿
02:21查看AI文稿AI文稿这是一道五年级必考的基础题,首先我们来看题, 如图,大正方形和小正方形边长各为七和五,求图色部分面积。我们来看, 哎,这一道题也就让我们求这个橙色三角形的面积,那我们看到求图形的面积,第一个要想到用公式来求,但是这个橙色三角形它用公式根本就求不出来,那我们该怎么办呢? 这一道题我们有很多种方法可以给他求出来,我今天就给大家说一说两种方法。好,我们来看。第一种方法就是我们来看,既然直接求我们求不出来,我们就反过来 用逆向思维先算大的这一个面积,然后再减去旁边这两个空白的。好,那大的我们就把它分成两个部分,一个是大正方形, 还有一个是这边的直角梯形。好,那这个大正方形能不能求出来?能,这个梯形上底告诉你了,下底也告诉你了,高也告诉你了,也可以求出来。 好,那我们把它相加,是不是就是这个大的面积?我们再看这两个涂色不,这两个空白的面积能不能求出来?能。好,那我再把它一相减,是不是就出来了?但是这个方法有点复杂,那我们再来看一看第二种方法。 好,我们来看这一条线是不是就是这一个大正方形的对角线?那我们就在这里这个小正方形给他也做一条对角线, 那现在这一条线跟这一条线他平不平行?是不是平行?好,那我们再把这个顶点给他拉过来,拉到这里,那是不是 我们这个橙色部分面积就等于这个三角形的面积?那是不是就是七乘以七,然后再除以二等于二十四点五?那么这道题我们就解出来了,关注我,学习更多好方法。
15一梦思维训练厅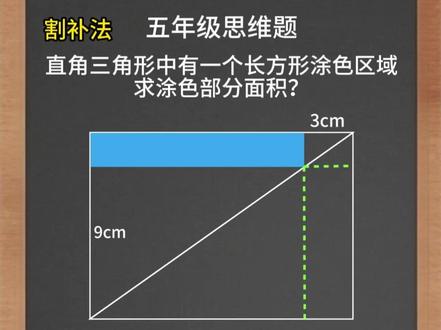 01:21查看AI文稿AI文稿
01:21查看AI文稿AI文稿五年级的几何题,想要比别人更加优秀,就要多看多做。下面这题看似简单,其实缺少条件,需要我们创造条件。题目只告诉我们两个三角形的各一条边,想求其他边不现实。有家长说用相似三角形来解, 但是这个知识点超纲了,我们就用小学生会的方法各补法。我们把圆三角形复制一份,以斜边为轴,反转到下面,和原本的三角形组成一个大的长方形,再延长涂色长方形边长,形成一个新的小长方形。 有同学说,怎么肯定是长方形啊,因为这是直角三角形啊,所以这条线是这个长方形的对角线。 这个时候我们看到这两个小三角形,这两个长方形,还有这两个大三角形,是不是大小都相同?既然相同,只要求出下面这块区域的面积,就能知道涂色区域的面积了。 因为这里是垂直的,这两条线又是平行的,所以这里也是三厘米,同理,这条线就是九厘米,所以这个新的小长方形面积就是二十七平方厘米,所以涂色区域面积就是二十七平方厘米。
69昭爸聊思维 01:49查看AI文稿AI文稿
01:49查看AI文稿AI文稿只要你学会了等高模型,也就是我们所说的拉窗帘,那么这道题对于你来说就是小菜一碟。首先我们来看题, 如图,大正方形和小正方形,大正方形边长为八,求图色部分面积。我们来看这一道题,也就是我们求这两个橙色三角形相加的面积。 一道题目他给的你已知条件越少,那说明这道题其实就越简单。我们来看,哎,他现在只告诉我们这个大正方形边长是八,那我们该怎么办呢?来, 我们先来看这一条边,他和下面的这一条边是不是相等。 好,我们再来看这一条边和这一条边他们是不是也相等, 那我们就把这一个橙色的三角形给他翻转九十度,是不是就变成了这样? 好,那实际上这一个橙色的小三角形是不是和这个面积就相等?我们要求的其实 这一个三角形就等于是这个三角形。我们来看,那现在是不是就简单了?我们就用等高模型,这两条线是一对平行线,我们就把这一个顶点给挪到上面去, 那实际我们要求是不是就是这个正方形的一半,那也就是八乘以八再除以二等于三十二,那这道题我们就解出来了,关注我,学习更多好方法。
33一梦思维训练厅 01:55查看AI文稿AI文稿
01:55查看AI文稿AI文稿这是一道五年级必考的求部分面积的题目,首先我们来看题, 如图,大正方形和小正方形边长之合是十二厘米,求图色部分面积。我们来看这一道题,也就是让我们求这一个橙色三角形的面积,那现在他只告诉我们这一段线段是二厘米,还有下面这里是十二厘米, 那很多人会想到拉窗帘这一条线和这一条十二厘米的线段,他们两个平行,那很多人就会把这一个顶点给他拉到这里,变成这样, 那实际上这一个成色部分面积就是这一个正方形的一半,但是实际上呢,这个正方形我们也不知道它的边长,也求不出来它的面积,那我们还是没有算出来, 那我们到底该怎么办呢?我们来看他还告诉我们这一条是二,那我们来看我们可不可以就把这一条边给延长。 好,那现在我们先不看这一半,我们只看这一半的话,我们来看 这两条线他是不是平行,那我们就把这一个顶点给他拉上去,那这两个三角形他们的面积相不相等?相等,因为他们同底等高。那现在实际上我们要求是不是就是 多一个三角形的面积,那就是十二乘以二,再除以二等于十二,那么这道题我们就做出来了,关注我学习更多好方法。
23一梦思维训练厅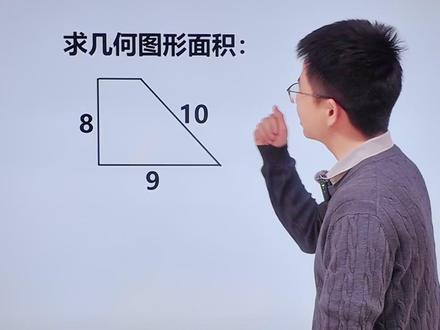 02:01查看AI文稿AI文稿
02:01查看AI文稿AI文稿看这道题,求几何图形的面积,那像这种五年级的压轴题,只要我们掌握勾股定力,就是可以秒出答案的。勾股定力虽然不是小学校内的必修,但作为课外的必修和初中的必考点,还是值得去记的。那勾股定力呢,要求就是直角三角,任意的直角三角形,比如说它的两条直角,边是 a 和 b, 斜边是 c, 那 么就满足 a 的 平方加 b 的 平方等于 c 的 平方,而满足条件的 abc, 我 们就叫做勾股数。那常见的勾股数呢,我们一起来复习一下啊,三四五三的平方加四的平方等于五的平方,当然我们知道一组勾股数之后呢,我们可以直接进行扩倍,比如说乘二 得到六八十,当然你还可以继续去扩倍,然后呢我们还可以回顾一些其他的,比如说五的平方加十二的平方等于十三的平方, 当然还有七二十四,二十五,那这些呢,都是我们常见的勾股数,大家一定要记得。那复习完勾股定律之后呢,我们接下来来看这一道一个梯形的面积,那我们可以直接用梯形的面积公式,也就是上底 加下底,乘高除以二,那么高是多少呢?是八,下底呢是九,那我们唯一缺的就是上底, 也就是上底,有了之后呢,这道题就轻松解决了。好,那上底怎么求呢?在这个时候呢,我们就可以用勾股定力呢来秒杀了。勾股定力要求直角三角形,那梯形当中,我们可以非常轻松的切出一个直角三角形来,在这里再做一条高, 我们就可以把一个梯形切成一个长方形和一个直角三角形,那它的斜边就是十,然后呢,这边是高,高的话呢,就是八,所以十和八哪个勾股数呢? 明显是六八十,我们另一条直角边就是六了,那这一段是六,整体是九,那剩下这个不就是三吗?它是三,它是一个长方形,这里也是三。那梯形的上底咱们就清楚了,那我们上底呢,就直接给它写成 三,直接计算三加九等于十,二乘八除以二就等于乘四,然后呢,最后这个结果就是四十八。这道题用勾股定律秒杀,你学会了吗?
 02:11查看AI文稿AI文稿
02:11查看AI文稿AI文稿听说你的几何能力很强,那你能不能秒了这道题呢?我们来看已知这两个正方形的边长分别是三和六,让我们求阴影部分的面积。 这里阴影部分是一个三角形,它的底我们已经知道了是小正方形的边长三,可是它的高我们不清楚,也没有办法通过已知条件来求出阴影部分的面积。 还记得之前我们学过的等高模型吗?现在我们连接 c、 b, 连接 c、 b 之后,我们就得到了一个大的三角形 abc, 它的底是三,高是六,所以它的面积就应该是三乘六除以二等于九。 大家发现了吗?三角形 a、 b、 c 被 d、 b 分 成了两个三角形,分别是三角形 a、 b、 d 和三角形 d、 b、 c。 这两个三角形我们可以看作是两个等底不等高的三角形,我们都以 d、 b 为底,三角形 a、 b、 d 的 高就应该是三,三角形 d、 b、 c 的 高就应该是六, 所以三角形 d、 b、 c 的 面积就是三角形 a、 b、 d 面积的二倍。 三角形 d、 b、 c 的 面积是三角形 a、 b、 d 的 面积的两倍。所以我们就可以将三角形 a、 b、 d 的 面积看作是一份,那么三角形 d、 b、 c 的 面积就应该占了两份, 所以三角形 a、 b、 c 就 一共占了三份,三份一共是九,所以一份也就是三角形 a、 b、 d 的 面积就应该是三。 同学们,这道题我们利用了等高模型来解决,当两个三角形的底相等时,它们对应高的倍数关系就是面积的倍数关系,你们学会了吗?关注雨,下期更精彩!
186玥玥宝贝成长记 00:24查看AI文稿AI文稿
00:24查看AI文稿AI文稿五年级寒假会做这道题,开学不愁成绩会退步,暂停思考三秒时间到涂色阴影部分的面积等于三角形 a e g。 加上正方形 b c, d e。 减去三角形 c, d, f 就 可以列出算式评论区告诉我你的结果吧。
 01:30查看AI文稿AI文稿
01:30查看AI文稿AI文稿如果你学会了蝴蝶模型,那这道题你就能秒出答案。首先我们来看题, 如图,长方形 a、 b、 c、 d 长十二,宽八 c、 e 等于六,求 c、 e、 f 面积是多少? 我们来看这一道题,也就是让我们求这一个橙色三角形的面积,那我们看到求这个部分面积呢?我们就先要想到用公式它能不能求出来,但是我们发现这个面积用公式它是求不出来的, 那我们该怎么办呢?我们就要运用到今天用的方法,蝴蝶模型。首先我们要做一条辅助线,怎么做?将 a 和 d 这两个点连接好,那我们来看 c、 e、 f 也就是我们要求的这一个三角形,它是不是和 a、 e、 d 这个三角形它们两个的面积相等,那所以我们要求这一个三角形的面积,我们相当于就是求 a、 e、 d 的 三角形的面积。 好,那 a、 e、 d 的 三角形我们就用公式就可以求出来了,以这一边为底,那它的底就是八减六, 以乘高除以二,乘以十二,再除以二就等于十二。那么这道题我们就解出来了。关注我,学习更多好方法!
21一梦思维训练厅 01:23查看AI文稿AI文稿
01:23查看AI文稿AI文稿这道题作为五年级的压轴题,难度大,分值高,但只要掌握了勾股定律,我们可以一秒解题。勾股定律虽然不是课内必修,但作为课外必修和初中必考,我们还是需要掌握的。什么是勾股定律呢?在直角三角形当中,两条直角边为 a 和 b, 斜边为 c, 三个数必须满足 a 方加 b 方等于 c 方的关系。那我们常见的勾股数有三四五,再进行扩倍就是六八十。除了扩倍这种方式,常见的还有五十、二十三、七二十四、二十五。 大家把这些勾股数记录下来做题会非常的方便。下面我们看这道小题。这是一个梯形,那么梯形的面积公式是上底加下底乘高除以二, 但是在这里上底是多少我们并不知道,下底为九,高为八,最后别忘了除以二。那这个上底该怎么去求呢?如何利用我们的勾股定律?其实每一个梯形都可以分割成一个长方形和一个直角三角形,在这个直角三角形中,斜边为十, 一条直角边为八,那另外一条直角边可以根据勾股定律求出来,当然就是六八十的这一组勾股数,那这边的长度就是九减六等于三,我们就找到了这个梯形的上底为三,最终求出它的面积等于四十八。这道题你学会了吗?
35杨思凡数学思维 03:29
03:29 01:22查看AI文稿AI文稿
01:22查看AI文稿AI文稿你在干嘛?呃,很烦躁。哎呀,做数学题吧。行,今天做哪一题?今天讲第十一题,两头模型。看一下题,两 头模型的原理就是先找到这两个三角形的共用角,也就是 c 这个点,它这里的平角,然后这个 c 对 应 abc 这三角形的两个边和对应 c、 d、 e 这三角形两边,他们之间的比相乘就等于整个三角形面积之间的比。然后通过这些可以知道 bc 等于两个 d、 e。 啊,不对, c、 d 的 话就可以写成一,一个 bc 就 可以写成二。 螺纹里 c、 e 和 a、 c 的 关系也是这样的,那从这里我们就可以知道三角形 c、 d、 e 的 面积比。三角形 a、 b、 c 的 面积就等于一乘一,比二乘二,也就是说 s 三角 c、 d、 e 是 s 三角 a、 b、 c 的 四分之一,而这 s 三角意思其实就是它的面积。好,那我们知道 a、 b、 c 的 面积是十二,那就可以知道 c、 d、 e 的 面积是十二,除以四等于三。 好好好,你写,你写你的呀。 啊,这就是结果。可乐,你听懂了吗?对啊,可乐,你听懂了没?我没听懂哎,扣一分。
10orange 03:07查看AI文稿AI文稿
03:07查看AI文稿AI文稿这是一道小学五年级求部分面积的题目,这道题目虽然难度很大,但用的知识很简单。首先我们来看题, 如图,已知正方形边长为十厘米,求图色部分面积。好,我们来看这一道题,也就是我们求这个紫色的面积。好,那这个紫色部分它是一个不规则四边形, 他告诉我们条件只有这一条是三厘米,这一条是四厘米,还有这个正方形的边长为十厘米。 好,那现在如果我们把他的对角线给连接,是不是还是求不出来?那我们该怎么办呢?我们就需要做辅助线,首先我们来做一条跟这一条线平行的辅助线。 好,然后我们再做一条跟这一条线平行的辅助线。 好,那现在我们看这中间是不是有一个小的长方形,我给他标为一,那这个一号小长方形,他的面积求不求得出来?求得出来是不是就是三乘以四等于十二。 好,那现在我们我就把这一个正方形除去一号小长方形以外的这一些部分,分成四个小部分。 好,我们现在来看,我已经将它分成了四个部分。 我们来看在这一个小长方形里面,二和二一撇这两个小三角形,它的面积相不相等。我们再来看这一个长方形里面, 三和三一撇这两个三角形的面积相不相等,相等,那同理这两个长方形里面的两个三角形都相等。好,我们来看, 那么现在我们是不是能知道,在这个大的正方形里面,除去这个一号长方形,他就是空白部分的两倍。好,那现在这个大正方形的面积就是十乘十 等于多少?等于一百。好,那么现在我们减去这个一号小长方形的面积,就是一百,减十二等于多少?等于八十八。 好,那八十八再除以二,是不是就是这个空白部分的面积四十四,那现在我们就是用一百减去四十四,是不是就是等于五十六? 那么这个五十六就是这一个不规则四边形的面积。那么这道题我们就解出来了,关注我,学习更多好方法。
26一梦思维训练厅 01:04查看AI文稿AI文稿
01:04查看AI文稿AI文稿这是一道小学五年级基础的求部分面积的题目,首先我们来看题, 如图,大正方形和小正方形边长分为八和六,求图色部分面积。 这一道题大家不要复杂化了,我们只需要用公式就能把它求出来。我们来看他就是让我们求这一个橙色三角形的面积,那现在我们以这一边为底,也就是这一个大正方形的 边长,也就是八,然后他的高就是我们把这一条边给延长, 然后再再做一条高,那这里其实就是八,减去下面这一条的六。 那么现在我们就知道三角形的面积公式就是底乘高除二,那么这个橙色三角形的面积就是,那么这道题我们就解出来了。关注我学习更多好方法。
23一梦思维训练厅 00:45查看AI文稿AI文稿
00:45查看AI文稿AI文稿五年级常考的几何题,尤其是阴影部分,求面积。不少孩子解题没头绪,那是因为几何思维没得到训练,但凡期末能考满分的孩子,都在考前把这类题摸透了。就是这本几何三十六模型,把小学需掌握的几何题型全分类梳理好了。 像三年十九考的一半模型、三年二十九考的等级模型、三年三十八考的小鹿模型、沙漏模型等全都有。 每个模型都有详尽的推导步骤,搭配视频动画演示,让复杂几何形象化,孩子直观易懂。还有核心母题解析和触类旁通的练习,不会的扫码看,免费讲解。让孩子掌握一个模型就能解一类题型, 还配套一本练习册,查漏补缺一套书,从四年级用到六年级,赶紧给孩子备上吧!
7小毅同学
猜你喜欢
最新视频
- 4152甜馨儿人工受孕一次成功




