24数学新高考一卷立体几何答案
粉丝487获赞2539
相关视频
 05:14查看AI文稿AI文稿
05:14查看AI文稿AI文稿这是刚结束的二零二四年新高考一卷的立体几和解答题,我们一起看一下这道题难不难。首先看一下题目四人追 p a、 b、 c, d 中 p a 垂直于底面 a、 b、 c d, p a 等于 a, c 等于二, b, c 等于一, a, b 等于根。三、 我把条件标在题目上,可以看出角 a、 b、 c 为一个直角。接下来我们看一下第一问。若 a 的垂直与 p b 证明 a 的平行与 p b、 c, 这是 a 的,它是垂直与 p b 的 证明。因为 p、 a 垂直于底面 a、 b、 c, 所以 p a 是垂直于 b、 c 的。 又因为 a、 b 方加上 b, c 方等于 a、 c 方,所以 a、 b 垂直于 b, c, 又因为 p a 交 a, b 等于 a, 那么 b、 c 就垂直于平面 a、 p、 b 同样,我们证明一下 a 的 p a 是垂直于 a 的, p b 也是垂直于 a 的。 p a 交 p b 等于 p 点,所以 a 的垂直于平面 a p、 b 因为 b、 c 也垂直于平面 a、 p、 b 垂直于同一个平面,两条直线平行,所以 b、 c 是平行于 a 的。又因为 b、 c 是属于平面 p、 b、 c, 所以 a 的平行与平面 p、 b、 c。 这是第一问。接下来我们看一下第二问。在题干中的条件下,这里又给出了 a 的垂直与的 c, 这里是一个直角且二面角 a 杠 c、 p 杠灯的正弦值为七分之,根号四十二,求 a 灯。我们先建立坐标系,如图所示,建立 a 杠 x y z 空间坐标系。 我们先过 der 点做 a、 c 的垂线垂足为一。我把三角形 a、 d、 c 的平面图画在下面,过 der 点 做 a、 c 的垂线垂足为一,并设 a 的等于 t。 我们可以从这个平 前面图形看一下,这一个边为 tac 是等于二的,这里又是直角。根据摄影定理, a 的方式等于 ae 乘以 ac 的,所以这里的 t 方等于 ae 乘以二, 所以可以得到 a, e 四等于二分之 t 方。勾固定理可以得到 a, e 四等于根号下 t 方减去四分之一倍 t 的四次方的。所以这时我们就可以找点的坐标 p 点的坐标零零二, c 点的坐标零二零 de 点的坐标 x 是负的,得一长度, y 的坐标是 a 一的长度二分之梯方, z 轴是等于零的, p, c 向量是等于零二负二 二 d c 向量根号下 t 方减去四分之一 t 的四次方,二减去二分之 t 方零,然后射出平面 d、 c, p 的法向量。 根据发销量垂直于 p, c 都是建立方程组 减得法销量 n 一是等于, 同理,我们可以得到平面 p a、 c 的发香量, 四为一零零。因为我们由法销量得到二面角的余弦值,所以我们先根据正弦值算出余弦值。因为三 inset 是等于七分之根号下四十二,这里可以看出这一个二面角为锐角, 所以扩散 inset 等于根号下一减。 say inset 方等于七分之根号七。那接下来我们可以用两个法相量表示它的二面角了。 所以扩散与 c 塔等于 n 一乘以 n 二的数量级,除以 n 一的模和 n 二的模等于七分之根七代入 n 一, n 二项量可化减的 t 的四次方减去七倍 t 方加上十二等于零。可以选择 t 方等于三或者 t 方等于四及 t 等于 根,三或者 t 等于二。但是 a 都是直角边, ac 是斜边等于二,要舍去最终 a 都是等于根三的,这是这一道题目。
1349我是小余 06:56查看AI文稿AI文稿
06:56查看AI文稿AI文稿hello, everybody, 今天我们继续学习立体几何,咱们来讲一讲如何在二维的纸上画出一个漂亮的三维立体图形。咱们就拿最简单的这个正方体来说,我左右各给大家画了一个正方体, 我奶奶也能看出来,是不是左边这个好看些,漂亮些,美关系右边这个,哎,虽然这个线段呢,也是一些线段,虚线呢,也给你画好了,但是你怎么看他都不像个正方,所以同样是正方,差别咋这么大呢?显然对于一个给定的力度性,不是你想咋画就咋画的。咱有一个标准,这个标准画法的名字叫斜二侧画法, 比如啊,咱知道,呃,正方体底面,呃,按理来说,任何一个面它都是一个正方形,那当我在空间当中画的时候,你看这个底面是不是,哎,这,这变成平行四边形了,这中间咋转化的?就是斜二侧画法,干这事,他说白了就是一种标准,你就像学说明书一样去学他, 比如我们好好的一个平面直角坐标器上,我给你画一个等腰三角形出来,那当我把它放到三维空间里面的时候,我们做这几件事,第一,把垂直的 x 轴 y 揉,这不九十度吗?现在变成四十五度, 哎,在这个空间里面,哎,你看着像那么回事啊,这两条线看,这是垂直的哈。第二步,所有平行于 x 轴的线段,比如说这个线段,平行于 x 轴的就在 x 轴上,它在前后二维和三维空间画法当中长度是不变的。但是平行于 y 轴的线段,比如说就拿这条线来说,它就在 y 轴上,我们为了画图美观,在新画法上要求把这段长度除以二, 比如说原来在图形上,这个长度如果说是两厘米,那现在在这个新图形上,它的长度就变成一厘米了,我们发现在空间当中这样画图 比较美观。最后一个来说,这个正方底,你这底面怎么画出来的呀?实际人家,原来啊,在二维空间上,它的底面呢?啊,是一个正方形,但是画在三维空间当中,原本垂直的两条线段,比如一个是 x, 一个是 y 啊,哎,你不能垂直啊,你得给我现在形成 四十五度了,然后平行于 x 轴上的啊,这个就是 x 轴上,它的长度在新图形当中是不变的,直接拉下来,但是平行 y 轴的线,我现在再在 y 轴上画的时候,长度要减半了,所以大致,哎,大致我就这么画一下,然后两条边都确定了,那这是个正方形的另外两条边平行着画喽,这底面就让我画出来了。 ok, 那 我们回过来继续往后讲啊。现在我来问大家,既然一前一后有这样一个对应关系,那前后图形这个面积有没有什么关系?比如就拿这个三角形来说,他们两个的把它当底吧,底的长度是一样的,是吧?比如说我都设成 a 好 了,他俩的高一个高,这个高呢?我设为 h, 那 新的这个三角形里面,它的高在哪?注意实际的情况上,你这是高,对应着,对应着这条线段是高,对不对?但是呢,我现在研究的是这个图形本身啊,这三角形这当底的时候,高是谁高?高得做垂直对不对? 我仅是把这个长度求出来啊,我看一看这个关系,放大一点,我想看它的长度,我就把它放到三角形里面,我们刚才知道,哎,这个三角形,这是直角,这四十五度,这不等于要直角三角形吗?那按照标准说啊,你这个长度是 h, 那 我画的时候这个长度就说应该是变成它的一半来着,它应该是二分之 h 有 了斜边,那我这个直角边就是在它的基础上再除个根号二,也就是二倍。根号二分之 h 有 了, 原来 s 一 撇是二倍,根号二分之 h, 那你看他俩是差几倍关系,是不是正好差的应该是二倍根号二的关系,记住了, s, 这个记为。啊,原来的图形面积叫 s 圆,它是二倍根号二倍的。这个新图啊,新图呢,我们称之为叫三维空间内的直观图,起个名叫 s 直,它有一个固定的比例关系, 三角形,这样四边形、五边形、六边形全都满足这关系,我不给他吸正了啊,你记住就行,因为你想嘛,你多边形,那我是不是可以拆成一个个三角形,它是用一个个三角形拼起来的呀?所以这个直观图和原图面积关系,有的时候就能用来做题。 咱先来看一道简单题,二零二五年上海的期中考试,它现在有一个水平放置的平面图形,它的直观图啊,这不就直观图吗?斜不楞登的是不是?三维空间内的?它是什么呢?是一个底角为四十五度,腰和上下底均为一的等腰梯形。哦,原来这个图形在直观图里面,它是等腰梯形。 这四十五,这四十五啊,这一,这一,这也一。那我问大家,你直观图里面是等腰体型,你实际在真正的平面直角坐标系里面,你还能是等腰体型不?显然不是,你前后图形形状那是大改变的对不对?正方形都能变成平行四边形路,所以原来它图形长啥样?哎呀,这个我们一会来说一说啊。但这道题人家没问你长啥,人家问的是 该平面图形啊。就是就是,这人原本的真正的那个平面图形,它的面积是多少?人问的其实就是 s 元。那我是不是能通过这个,我直接把 s 一 撇先求出来, 乘个二倍根号二呗,简单变成小学数学了。上底是一,腰也是一想学下底做个垂直直角边,一除以根号二,二分之根号二,左右对称的中间是一,所以下底应该是一加根号二。 s 等于上底加下底一加一,加根号二,乘以高高是二分之根号二,最后再除以二。 我最求的 s 圆就是它在乘以二倍根号二。约啊,全约掉二加根号二,这是我们的第一种解法,你都知道结论了是吧?哎,但是你光做完题不行啊,我现在加大难度啊,我要求大家,你这不是直观图吗?你现在把它的平面图,也就是在这个直角坐标系当中的真正的那个图形给我画出来, 开始画你这四十五,我这就垂直 x 轴,长度一加根号二。那我现在也是啊,那也画成一加根号二。好,那这个四边形的两个我是不是先确定它比较好,确定 怎么画呢?有的人说,啊,这这个我这样画,那你大错特错,为什么?因为你这个点啊,就是无论你怎么转化,你这个点现在在 y 轴上,转化完在 y 轴上,你转化之前是不是一定也在 y 轴上啊?你图形的性质不能变啊。 你这个变原来在 y 轴上,你现在转化完也得在 y 轴上,你这在 x 上,也得在 x 轴上,你不能转化着转化着跑偏了,是吧?所以这个点对应到原来上也得在 y 轴上,但是它的这个坐标的长度是多少长度?你得是你这个长度的两倍,这个长度 是一,那他的两倍就是二。那现在已经三个点都确定的情况下,第四个点什么位置?首先上底跟下底肯定是平行的,对不对?还是那句话,因为我转化前后,他的平行性质不能发生改变啊。垂直有可能发生改变啊,因为因为你这原来垂直的,现在现在都不垂直了,但平行不能变,咱还得平行的话,但是具体伸出去多长咋说的来着? 跟 x 轴,这不就问 x 轴平行的线段吗?跟 x 轴平行,线段变化前后长度不能变呐,所以这也是一因此。原来呀,这图形它实际上是一个直角梯形,然后转化着转化着变成等腰梯形了, ok, 很 有意思的一道小题,再来一道, 刚才问面积,现在,哎,现在不问面积,问周长了。那这个时候呢?你没有这个公式,没有结论了,你就真得进行直观图和平面图之间的转化了。他给我的是 y 着的,这叫直观图对不对啊?他说啊,这个直观图怎么样呢? b 撇, c 撇, a 撇 c 撇,都是一。这两个啊,都是一。 a b 平行于 x 轴, a c 平行于 y 轴。 ok, 那 首先我能知道是你这俩平行,这俩平行,那你形成的这个角度得是一样的。所以说明,哦,原来这四十五,这也四十五,因为你是等腰三角形,你俩四十五,你这就直角啊,等腰直角三角形,一比一比更好。二, ok, 那 现在人家问我三角形 a、 b c, 我 刚才这是 a b 撇 c 撇 a, b c 指的是,是不是那个原来的那个平面图啊?真正的那个图形,那我就转化一下呗。 首先,呃,我在真正的平行当中, x 轴、 y 轴,那得垂直的。然后我问大家啊,你这三角形三边,你先画哪条边最简单?是不是跟 x 轴平行的?我不用动就好了。你原来是多长,我现在还是多长, 我就画一个根号二这个长度。接下来你说 a c 好 画还是 b c 好 画?傻子,你都得给我调 a c, 因为 a c 性质多的。摁它,它跟 y 轴平行呢?是不是平行性质不能变?你变化后平行,变化之前跟 y 轴也得平行, 但是长度注意,我画多长呢?你变化完是一,变化之前我得是你的两倍才对。所以我这个图案,这个这个纵坐标还真得画长一点,它的长度是二,这样画。那紧接着你三点多确定了,那最后一条边直接连起来就可以喽。他一会问我边长,我得求斜边根号下它方加它方是根号六,那二加根号二,加根号六,选 c 结束。
172一数儿的课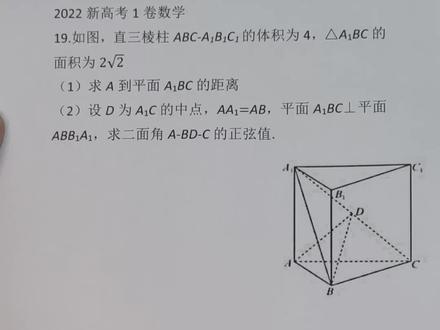 11:48查看AI文稿AI文稿
11:48查看AI文稿AI文稿好,今天咱们讲一下新高考一卷数学的第十九题,说有一个值,三棱柱在这,对吧?他的体积是四,然后他还告诉我,三角形 a 一 b、 c, 他的面积是一个二倍的根号二。然后第一问,让我们求点 a 到平面 a 一 b、 c 的距离, 那么看到这个,他告诉我体积的话,又告诉我这个面的一个面积,我是不是可以考虑用一个等体积法求高的方法,把这个面距离给求出来,对不对?好,所以说第一步我们先把这个大的一个三龙柱的体积表示一下。 好,它的体积是不是等于底面积乘以高啊?最后得到的结果应该是四,对不对?因为题中告诉我了。好,接下来我再把这个三棱锥 a 一 abc, 他的体积也表示出来。好,很明显,我知道三角形 abc 的面积乘以 aa 等于四,那么这个三龙锥的体积我们是不是不是也可以直接表示出来等于三分之一乘以四,等于三分之四, 那么好,这时候我切换一下他的面积表达方式。好,此时我不以这个三角形 abc 为这个三棱锥的底面啊,我考虑用三角形 abc 做这个三棱锥的底面, 那么这时候这个三棱锥的高是不是就是点 a 到平面 abc 的距离?所以说我设一个未知数啊,设 a 到平面 a, e, b、 c 的距离是 d, 好,射出来这个距离以后, 我换一种方式来表达他的体积。好吧,好,我们来看题干中 a、 b、 c 的面积,是不是他已经告诉我了,是不是一个二倍的根号二啊?那么这样的话,我是不是可以通过这个公式把 d 给求出来,对不对?那这样的话我们就知道, 好,这样的话是不是 d 求出来了?也就是说 a 到平面 abc 的距离就求出来了?好,第一问我们就解决了。 好,接下来我们来做一下。第二问,说点 d 呢,是这个 a、 e、 c 的一个终点,然后还告诉我 a、 a 一和 a、 b 长度是一样的,然后他又告诉我这个面 a、 e, b, c 垂直于侧面 a, b, b, e, a 一,然后让我们来求这个二面角 a、 b, d, c 的一个正弦值。 那么想解决这道题的话,我们是不是考虑用间隙的方法来做,对吧?哎,所以说这道题我的这个思路大致是这样的啊,呃,我们首先我们来看 bc 这条线是不是面 a 一 bc 和 abc 的一个交线啊,对不对?而这两个面是不是都都垂直于这个侧面,所以说这个 bc 其实也垂直于这个侧面,对不对?所以说我考虑。哎,先把这个条件写出来,正出来, bc 和 ab 是垂直的。好,那么我来写一下啊, 好,这个 bc 垂直于 ab, 我们已经。呃,正出来了,那接下来我们应该可以这样间隙了。但是还有一个问题,就是这些点的这个坐标我们该怎么表示?因为他们都没 没有告诉我他们具体的长度,所以说这道题需要想办法引入一个量来求出他们个点的坐标,对吧?这时候我考虑怎么样呢?我可以考虑过 a 点向 a、 e、 b 做一条垂线,我们来看看会有什么效果。 好,我们在这做一条垂线,我设这个垂组为 h, 那么我们这就可以写做这个 ah 垂直于 aeb。 好呢,根据题,我们知道这个 a、 b、 c 啊,是和这个 a、 b b 一 a 一这两个面是互相垂直的,那么这个 a、 h 又垂直于他们的交线,那么我们是不是就可以通过这个条件来推出 a h 垂直于面 a e、 b c 啊?所以说我把它写一下, 好,我写出来以后我正出来了, ah 是垂直于平面 abc 的,那么这样的话,我们是不是就知道这个 ah 其实就相当于第一第一位中的这个 d 啊?所以说 ah 的长度是不是有了 啊?所以说 ah 就等于这个 d 呗,等于什么?根号二是吧? 那 a h 的长度有了,我们看还有这个条件没有用,对不对?我们知道这个三角形 a e a b 是一个直角三角形,而且 a e a 等于 a b, 所以说它是一个什么三角形啊? 等腰直角三角形对不对?那对于等腰直角三角形的话,我知道他这个 ah, 他这个斜边上的高的长度,那么是不是他任何一条边的长度我们就都可以求了,对不对啊? 我就可以写啊,因为在这个直角三角形啊,直角三角形这个 a e、 a b 中啊,我们知道这个 a e a 等于 a b, 还有就是 a h 垂直于 a e b, 并且这个 ah 还等于一个根号二,所以我是不是就可以得到 aea 等于 a b 就等于钢号二倍的他,对不对?等于几啊?等于二嘛,对吧?然后这个 a e、 b 这个斜边对不对? a e b 就等于多少?就等于个二倍的钢号二。 好,我们再来看上边,我们是不是推出 bc 垂直于这个平面 abba 呀?就是 bc 垂直于这个侧面, 所以说我是不是可以得到 bc 也垂直于谁啊? aeb 啊,对不对?我可以写,因为这个 bc 啊,是垂直于平面 abba, ae 的,所以我们就知道 bc 是垂直于谁啊?垂直于这个 aeb 的, 那么好呢,在这个直角三角形啊,这个 a 一 bc, 那么我们就可以知道这个三角形 a 一 bc, 他的面积就等于二分之一倍的 a 一 b 乘以 bc, 对不对?等于多少?等于一个题干中告诉我二倍的根号二, 那么 ab 的长度有没有? ab 的长度是不是在这?是不是二倍的更好?二,所以我就可以知道 bc 的长度就等于什么?就等于四倍 的根号二,去除一个 aeb, 然后代数,最后求出来 bc 的长度是几就是二,所以说求出来呢,这么多长度了,那么各个点的坐标我是不是间隙以后就能确定了?好,接下来我们开始间隙啊,因为地方有线,所以说我又换了一张纸, 那么我已经把刚才咱们求的结果,比如说 ab 等于二, bc 等于二,包括他们的这个侧棱 aaebb, ecc 一等于二,他们的长度都已经标出来了, 那么接下来我就可以以 b 为原点,以 bc 为 x 轴,以 ba 为外轴,以 bbe 为 z 轴,我们间隙啊,好,那么这个轴呢?它是一个 x 轴,对不对啊?然后这呢是一个外轴, 好,然后上方这是一个这种画一点歪啊,好,那么我把这个写一下 好,建完戏以后,那么他们各自点的这个坐标,我是不是就可以标一下了?比如说 c 点的坐标,他是不是就是一个二零零啊?然后这个 b 点坐标,当然他是远点了,对不对? 然后这个 a 点坐标,他相当于就是一个零二零,那么这道题这个 b 一点我用不到,对不对?那么我把 a 一点的坐标不要写 a 一点的坐标,呃,是一个零二二, 最后这儿这个地点我也要用到,对不对?题中告诉我,这个地点是一个 a、 e、 c 的终点,那么地点坐标是不是就是 a 一和 c, 他们坐标之何在?除以二啊,对不 对?那么就是他们相对应的坐标之和除以二,其实就是一一一。好,那么他们各自点的坐标我标出来啊,对吧?那接下来呢?我这个设设出这个两个平面的法项量,我们要求的这两个平面的一个法项量。好,我先设 这个平面 abd 啊,这个平面的发现量,好吧,设这个 n 为他的发现量, 同样道理,我设这个 m 项链啊,是另一个面的法项量,对吧?用 x 零 y 零 z 零来表示, 好射出反向内以后,我们把他们给求出来,对吧?呃,首先我们知道这个 n 项量,对不对?他应该是乘以这个 b a 项链等于零,还有一个是 n 项量去乘以一个 b d 项 项链,对吧?应该等于零。那么因为 b 点是原点,所以说 b a 项链和 b d 项链的这个值,其实就是他们的一个坐标的值,对吧?所以说我一乘就可以直接得出结果。呃,得到第一个,首先得到一个二 y 等于零, 对吧?第二个得到一个 x, 加上 y, 再加上一个 z 也等于零,那这样的话,我可以推出啊,得到一个就是 y 等于零,然后 x 等于负 z, 然后我另这个 x 等于一,那么我就可以得到这个 n 项量, 他相当于是一个一零负一,同样道理,这个 m 项链,对吧?他应该乘以谁啊?乘以 b c 项链等于零,对吧?还有一个 m 项链乘以一个 b d 项链也等于零,对吧?那么把数带进去以后, 可以得到,一个是 x 零等于零,另外一个是 x 零,加上 y 零,加上 z 零等于零,这样的话,我就可以得到啊,这个 x 零等于零,然后这边是一个 y 零等于负 z 零, 然后我让这个 y 零等于一,对吧,就可以得到这个 m 项量等于一个零一负一。 好,下一步我们求一下两个法项量夹角的鱼线值,对不对?那么我们求那个正的值吧,所以说就是一个扣赛啊,这样绝对值。这个 m m 项链和这个 n 项链的一个,呃,夹角的鱼线值,他等于什么呢?两个的项链的基对不对? 两个下量的机除以他们的膜啊,除以他们膜的机,对吧?好,然后等于什么呢?哎,我们来看 看一下,一乘零零,一乘零零负,一乘负一就就是一,好,下一边呢?呃,这个,他的这个魔长是不是一个根号二,对吧?呃,这边是一个根号二,然后这边也是一个根号二,所以说他的结果应该等于多少?等于二分之一, 对不对?好,那既然他们夹角的这个鱼线值啊,我们算的那个正值是二分之一,那么他们夹角的这个正线值对不对?我们是不是就得到了?应该等于多少?是不是应该是一个二分之一个号三呀? 好,那么我们知道啊,因为这个法项量啊,他的这个夹角与二面角互补,对不对? 好,所以我就可以知道这个二面角 abd c, 他的一个正弦值也等于多少二分之二十三。好,所以说这道题的结果就是这个。
1300小杨数理化 12:12查看AI文稿AI文稿
12:12查看AI文稿AI文稿我们来讲解一下二零二三年新高考数学全国一卷立体几何这道大题。立体几何考了这么多年,每年都是间隙设点,毫无新意。在一个四轮座,其实就是说底面呢,是一个正方形,那么它的边长呢?是二, 然后他的侧棱长是四。好,有这两个条件,我们可以直接间隙设点,建立如图所示的坐标系,对吧? x、 y、 z 这三个方向。然后呢,又告诉一些边长, 好,他,他和他,而这三个长度呢,方便我们去描述点的坐标。其中啊,这一段他的长度是一个一,然后呢,这个这个的长度是二,等于这段长度 也是二。好,还有一个长度是这个, ok, 那么这个长度是三啊。大家想一下,有了他,他和他,那么其中这个点,这个点,这个点和这个点,他们的坐标是不是直接可以写出来了? 好,根据我们建立的坐标系啊,我们把第一问用到的这些点的坐标全部给他描述出来。好,首先 b 二是零二二,其次 c 二是零零三。再来啊, a 二是二二幺 d 二二零二,这一步不要出错,这一步出错就全完了,后边都不用做了啊。好,接下来我们把这两项量算一下, b 二、 c 二这个项量,他等 于 c 二的坐标减去 b 二的坐标零负二一。好,同样的道理,我们再来算一下, a 二、 d 二这个项量也是零负而已,那么这两个项量是平行的, 所以呢,我们就直接证明出来了, b 二和 c 二,他们在和直线的是互相平行的。好,这是第一问,第二问呢,难度不大,但是计算量非常大,当然这个计算不要笨,算他也是有技巧的。 a, 那么接下来呢,我们来做一下这个第二问号,看一下第二问,首先注意题目,他说的是哪个二面角呢? p a 二 c 二 d 二好,是这个二面角,那么他涉及到一个新 的点,这个点呢,在 bb 一上面运动,所以我们可以直接把这个点的坐标给他设出来。好,假设点 p 的坐标就是一个零二 b, 因为这个是未知的,所以他就可以在 bb 一上面去运动了。 好,然后呢,我们要去求这个二明角,就要去求把项链,求法项链,看一下需要用到哪些项链 好,通过二面角找我需要的项料有两个平面啊,那么在第一个平面当中,我们可能会用到 c 二 a 二项料, 还会用到 c 二 p 香料好至第一个平面,那么第二个平面也是同 通过二面角,直接通过这些角标去找,可能会用到项料, c 二 a 二项料啊,以及 c 二,他这个项料和这个项料。 c 二 d 二项料。好,刚才那个可能会用到这个项料和这个项料。 那么接下来呢,我们电梯的坐标知道了,那么通过第一问呢,我们已经把 c 二、 d 二、 a 二这三个点的坐标啊,这是 c 二、 d 二、 a 二,他们的坐标全部都写出来了。 好,那么这样的话,我们就可以直接把这三个项链与它表示出来。好,我们来表示一下,首先 c 二 a 二项料,它等于 二二负二,好,再来 c 二 d 二项量,他等于二零负一, ok, 继续 c 二 p 项量啊,他等于零二 b 减三, ok, 接下来我们来表示一下法项量,假设第一个平面 a 二 c 二 d 二,那他的法项量如果是一个 m 项量是 x one z 法向量有一个很重要的性质,法向量是垂直于平面内的任何一条直线,那么它就垂直于我们用平面内的点表示的向量,所以我们就可以得到 m 向量, 点乘上 c 二 a 二项量,这个值是等于零的, m 项量再点乘上 c 二 d 二项量,这个也是等于零的。然后呢,就是项量之间的坐标,用算把他们给他算一下,就可以 得到二 x 加上二 y 减去二 y 等于零,好,其次,二 x 减去 y 等于零,好,根据这个和这个 三个未知数只有两个方程啊,那其实是算不出来的,但是我们可以复直去表示他们之间的一个关系。 好比如说第二式子得到二 x 等于 z 啊,那我其实可以假设 x 的于一,那么 z 就是等于二,再把它们带到第一个式子里边,算出 y 等于一,所以 m 项量等于一。一二, 好,同样的道理啊,同样的道理,我们假设呢?第二个的平面 a 二 p c 二,那么它的法项量 假设是一个 n 项量啊,我们用完全相同的做法,那其实 n 项量他是点乘上我的 c 二 a 二项量是等于零的。其次, n 项量在点乘上 c 二 p 项量也是等于零的,对吧?好,这个具体我们就 不写了,直接给大家。结论。 m n 项量呢,是等于一个二除以三减 b 减一,一,再来一个二除以三减 b。 好,两个项量,两个法项量,确切 的说都求出来了。接下来呢,根据二面角,那么题目呢?看一下题,题目说这个二面角的大小是一百五十度,对吧?好,我们能不能把这个 b 给他求出来了?当然是可以的,在这里呢,涉及到一个简单的几何知识啊, 那么现在我们知道这两个平面夹角呢,是一个冻脚,对吧?一百五十度,好,这是他的发现料,这是他的发现料,这垂直,这垂直,这一百五十度,那么他们的夹角的和这个一百五十是互补的,那么这个角应该是一个三十度。 好,也就说两个限量的假酒使三十度,那么他们的余弦值两个法向量,他们的余弦值应该是一个三十度的余弦值,就是二分之根号三。好,那道理是比较简单 的,这个项链点上这个项链,除以他的膜乘以他的膜,好,那么他这个结果就是一个刚才我们说的,哎,三十度的余先值二分之多少三, ok, 这是算式啊,接下来主要是计算。呃,那么用算量还是比较大的,首先 m 项量点上 n 项量, 用它去乘以它啊,横坐标,纵坐标,竖坐标分别相乘,再相加,你就得到了 二除以三减 b 减一加上一个一,再加上四除以三减 b。 好,这是向量的点乘。然后呢,再除以他们各自的模长, m 向量模长使根号六,然后再乘以这个啊,这个其实如果 通风的话,我们会发现分母都是三减 b, 对吧?好,刚好下,每一个都给他平小方。好,这一呢,我们简单了合并一下, 三减 b 分之二减三加 b, 那就是三减 b 分之 b 减一,对吧?好,他呢就是三减 b 分之 b 减一括号的平方加上一的平方,再加上二的平方除以三减 b 括号的平方。好,这个结果等于根号三比二, 注意到这个地方不要死算啊,看看有没有可以化解的地方,比如说加一减一是不是没有了?好,然后分母同为三解 b, 三解 b 分之六,那么下边这个,下边这个,我如果我们再多写一步啊,这是六除以三解 b, 对吧?然后呢,除以这边是根号六, 六乘以好,他根号下,这是平方,我们把分母全部通分,我们发现这是一个三角 b 的平方,如果给他开根,那开出来就是一个三角 b, 好,接地方,不用担心符号的问题啊,因为呢,我们已经推出来了这两个像量的夹角,一定是他的余弦值,一定是正的,是大于零的,而分母是大于零的,所以分子肯定大于零和三节臂就是大于零的, 那这样的话就可以大大解化我的运算。那开出来这分母是一个三解 b 这分子了,是一个 b 减一的平方,再加上,注意,这是一啊一的话,是不是三解 b 的平方,分之三解 b 的平方,所以这地方特别容易 错,注意,这不是一,这是三角 b 的平方, ok, 然后呢,再加上一个四啊,那么他输等于根号三比二, 然后注意三节臂和三节臂约掉根号六,除以根号六,剩一个根号六,根号六和根号三越下剩余根号二,然后左右两边同时给他平方 平方之后这根花儿变成了二,二变成了四,给他交叉相乘好,这是二,这是四,二,四得八,我们就得到了八,等于他的平方哦,乘以一个一, 他的平方就是 b 方减二, b 加一,再加上九减六, b 加上一个 b 方加上一个四,好,合并一下,这边是二, b 方减去一个八, b 这边是加十加八约一个,剩高二加串六等于零,就得到了 b 方减四, b 加三等于零。好,那这样因式分解, b 减一乘以 b 减三等于零,我们得到 b 有两个值,第第一个答案是一,第二个答案是三。 好,必算出来。注意看下题,题要我们求什么题?让我们求的是 brp brp 的长度,对吧?那 brp 怎么来求呢?注意, br 到 b 的距离是不是二,而我现在 p 啊,我们算出来了,小 b 是等于一或者三的。好,那小 p 的位置呢?在哪里?它的位置一个是倒点 b 的距离是一,一个是倒点 b 的距离是三,这段长度是三。那不管是一还是三,我 b 二 p 的长度 这一段,或者说这一段,要不呢就是三减二等于一,要不就是二减一等于一,不管是一还是三, b 二 p 的长度都是一,所以我们就得到了 b 二 p 长度等于一。 ok, 那么这道题我们就做完了。立体几何这道题思路很简单啊,有一定的计算量,难度呢,不大,只能说是一道比较常规的题目。好,今天分享就到这里,你做对了吗?
1296北京初高中数学李老师
猜你喜欢
最新视频
- 1539阿巾凡.














