lru算法四种实现方式介绍
入 case 类实现了路缓存算法。它使用一个 in order map 来存储舰制队。其中键是缓存的键直是一个 pair, 包含缓存的值和一个指向链表中对应节点的迭代器。同时还使用一个双向链表来维护最近访问的顺序。链表头部是最近访问的元素。链表尾部是最久未使用的元素。变方法用于获取缓存中指定键的值。 如果键不存在,返回负一。如果键存在,将对应节点移到列表头部并返回对应的值。 破方法用于插入或更新缓存中的建制队。如果建议存在,更新对应的值,并将对应节点移到列表头部。如果容量已满,删除最久未使用的元素, 并插入新元素到链表头部。在 main 函数中,我们创建了一个容量为二等入 case 对象,并进行了一系列的操作来测试录缓存算法的功能。
粉丝2030获赞1.3万
相关视频
 04:12查看AI文稿AI文稿
04:12查看AI文稿AI文稿那么说咱们来聊一聊 redis 的 l i u 算法,想知道它是如何实现的? l i u 算法呢,翻译过来叫做最近最少使用算法,它呢是一种内存数据的淘汰策略,那么最常见的场景呢是当内存不足的时候呢,需要淘汰掉最近最少使用的数据。 l i u 呢一般是用于缓存系统的一个淘汰策略,那他们是能讲一讲 l i u 的基本实现原理吗?举个例子,我们的内存压占大小呢是三,也就是说只能存储三个值,那么一开始呢,来了一个七, 这个时候呢,七就进入到了站的最下面,然后呢又来一个零,然后呢也进入了这个站下面,然后呢紧接着再来一个一,也入站了。那么到了最后这个时候呢,来了个二,这个时候呢,我们的空间呢其实已经不足了,那这时候呢,我们就需要淘汰最近最少使用的,也就是我们的七,我们呢就会将七淘汰掉, 然后呢我们再把二放进去,那么这个时候呢,占中的值就变成了二幺零,然后这个时候呢,零如果又被使用了,那么就要将零呢要放到最上面,然后这个占里面的值呢就变成零二幺。假如这个时候又来一个三,那么占里面呢又变成了三零二, 那么接着假设您又被使用了,您呢又会占用到最上面,接下来如果再来一个四,又会顶掉下面的二,就变成了四零三。大家可以看这个图的一个变化,那么当你把这个图看懂以后呢,相信你已经对 aio 的一个运算过程已经了解了,那 ready 使用的 ai 预算好像是怎样的呢? 问题是呢,对 l i o 的一个算法做了一些优化,因为传统的 l i o 算法呢,存在两个问题,第一个呢,就是数据的使用情况,需要额外的空间进行存储。第二个呢,会删除肉 k, 从而导致最希望命中的数据呢,可能会丢失。为了帮助大家在这个求职旺季顺利上岸,我特意 整理了一份 java 程序员求职初期手册,包含五十万字的高频 miss 题、简历模板和学习路线图,大家可以去评论区的字典中领取。为了避免这两个问题呢, reds 使用的抽样的方式对 liu 算法呢进行了一个优化,当然可能存在一定的精准度问题, 但是呢,根据官方的数据,当车辆数据达到十的时候,就已经非常接近传统的 liu 算法了。所以呢,在 regis 配置文件中呢,提供了一个属性叫做 max menery, 它的一个默认值就是五, 这个值呢是表示随机抽取五个 k 的值,然后呢,对这五个 k 呢,按照 liu 算法进行删除,所以呢,很明显, k 值越大,那么删除的准确度呢,也就越高。来看这么一段元代码, 它是表示我们 radius 的一个整体的数据对象。我们要注意到 radius 的底层, oppo 级的对象呢,他会拥有一个 liu 属性,那么他记录了对象的最后一次的使用时间,他是一个三个字节的二十四位的数据。我们在创建对象的时候啊,就会将 liu 的数据呢写入进去,那如果对象被重新访问, liu 呢也会同步进行更新。 我们的算法呢,就是通过当前的这个时间搓减去 l i 里面的这个记录的系统时间,那么得到那个差值最大的,我们就会把它删掉。然后呢, redis 呢,还做了一个小小的优化,在 redis 中啊,维护了一个全局的属性,叫做 l r u clock, 这个属性呢,是通过一个全局函数 sever crom, 它是每隔一百毫秒执行一次来进行更新的,那么它记录的是当前的这个 unix 的一个时间戳。这个时候我们就会想到,如果用真正的时间岂不是更加精准呢?这是因为 redis 希望在每一次更新 l i u 的时候是直接取全 数据时间出,这样的话就不用去调用系统的时间,从而去避免误差。而 liu 的属性的最大值呢,是二十四位,也就是说最多是一百九十四天,一旦超过了就会从零开始,这个时候呢,就会有概率出现 liu 的属性大于全局的时间出的情况。 于是呢, ratis 呢,他就设置了两种计算方式,当全局的 l i u clock 大于 l l 的时候,那么就使用 l i u clock 呢去减掉 l i u, 得到一个空前时间。那么当全局的 l i u clock 小于 l i u 的时候呢,就使用 l i u clock max, 也就是一百九十四天这么一个值去 减掉 i r u, 加上 i r u clock, 得到一个空降时间。以上呢,就是 redis 对 i i u 算好的一个优化,以及 redis i r u 的一个实现方式。感谢各位的关注和点赞,各位同款们如果还有需要补充的话,可以在评论区留言。
 01:58查看AI文稿AI文稿
01:58查看AI文稿AI文稿job 面试题,什么 l r u 请手写使用 link hash map 实现 l r u 缓存? hello, 大家好,我是架构师奶爸。 l r u 是 least recently used 的缩写, 它是一种常用的缓存淘汰策略。在 java 中,我们可以使用 linktash map 来实现 l r u 缓存。在 l r u 策略中, 我们保留最近使用的数据项,当缓存达到最大容量时,将最不常用的数据项从缓存中移除。这个算法是基于一个观察, 如果一个数据项最近被使用过,那么他很可能会在将来被再次使用。因此,当缓存接近其最大容量时,我们应该移除最近最少使用的数据项。在 java 中,我们可以使用 hash map 来实现一个简单的 l r u 缓存。 linked hash map 继承自 hash map, 它在 hash map 的基础上维护了一个双向链表,这个链表按照元素的插入顺序或访问顺序来排列元素。当我们访问一个元素时, 我们可以将它移到链表的尾部,这样就可以保证链表头部的元素是最近最少使用的元素。当缓存达到最大容量时, 我们可以删除链表头部的元素。以上是一个使用 linktash map 实现 l r u 缓存的视力代码。 在这个势力代码中,我们通过继承 linked hash map 并覆盖其 remove eldest entry 方法来实现 l r u 缓存。在 remove eldest entry 方法中,当缓存的大小超过其最大容量 时,我们返回 true 并删除链表头部的元素,这样我们就可以保证 l r u 策略的正确执行。想了解更多 java 架构师岗位知识,请关注我架构师奶爸,点赞转发收藏,共同筑基 java 架构师!
88架构师奶爸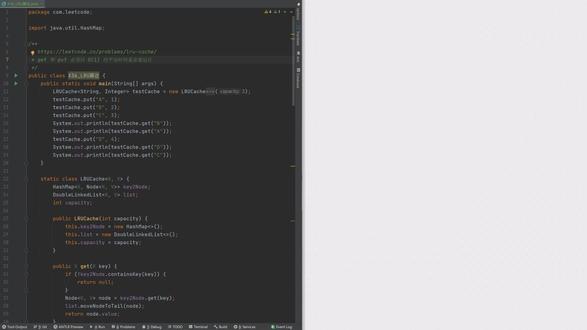 25:53查看AI文稿AI文稿
25:53查看AI文稿AI文稿哈喽,这道算法是怎么样?自己去写一个 liu, 实现一个 liu。 首先什么是 liu 算法? url 算法,它对应的是一个数据结构。比如说你给定了一个数据结构,这个数据结构的容量是四, 也就是你这个数据结构里边他只能存四个数据。如果你存的数据超过四,比如说来了第五个数据的时候,那他就要在这四个数据里边淘汰一个,把一个踢出去,然后再把这第五个数据加进来。 这中间就涉及到怎么去踢数据以及踢谁。这设计到一个顺序问题,比如阿优,他是怎么样的呢?比如说一开始你放了 abcd 四个数据对不对?然后当然 刚才那四个都是铺的操作啊,就是我们假设这个都是铺的操作,铺的进来四个操作之后,然后如果第五个操作他要铺的进来一个亿的时候,首先你这个亿元素在不在这个数据结构里边,首先他不在对不对?那说明他是一个新的元素, 他就是要把原先的某一个元素剔除掉,他自己加进来。那剔除的时候剔除什么呢? 剔除最远的这个 a, 因为 a 是最先被加进来的,这是相当于你可以把它看成一个时间线,谈不来,你可以把它看成一个时间线,就是 后加入的总是在后边,然后最先加入的总是在左边。然后 a 呢? 就是最不经常被访问以及他最早铺的进来的一个数据,这个时候就把 a 给剔除掉,然后让一加进来,这就变成了 bcbcd, 这这个这个 ofc 就变成了 bc 第一组成的数据。 然后比如说我们这是刚才第一个操作啊,比如说现在我又来了第二个操作。第二个操作是什么呢?我要 get c, 那这个时候只有 b, c, d、 e 对不对?我要 get c, get c 的时候。首先我 get 的时候, 因为我们提议吗?先看一下这个提议。 get 和铺的都要求他的欧一的时间复杂度运行欧一的时间复杂度对吧?我们先不要管这个复杂度,我们先把这个流程说一下。 然后我们首先要通过一个欧一的复杂度拿到,看这个 c 在不在这个里边对吧?如果他在这个里边,然后我把它拿出来的时候, 我要更新一下他的位置。为什么要更新他的位置?因为他这次被访问了,那说明他就是最先被访问的数据,我要把他移到最后边,这样就代表了就把他挪到末尾,就代表他是 最后被访问的那个数据。虽然你这个 c 在中间存在,但是你一旦被访问了,一旦被 get 了,我就要把你挪到这个末尾,这就是 uru。 然后下次下次,如果数据量满的时候,淘汰的 时候就不会去淘汰 c, 而是会去淘汰没有被访问过的前面的这些数据,比如说 d 啊之类的就会被淘汰。而 c 不会被淘汰,因为他不刚被访问过, 就是通过这个顺序的调整来保证他不会被首先淘汰。对,是这样的一个意思。那这个流程清楚了对吧?首先你铺的时候或者是 get 的时候, 都会把这个元素啊往后挪,这是这个思想。然后该用什么样的一个数据结构去实现它?这是第二个要考虑的问题。首先这就要考虑复杂度了。首先 get 和铺的都必须是欧一的复杂度,必须是欧一的复杂度。想 想到欧有什么出结构能达到欧一的复杂度呢?哈西麦普嘛?哈西麦普他能达能大,能够达到那个欧一的复杂度。 也就是我们去 get 的时候。比如说 get 的时候,我看这个 c 存不存在吗?也就是他砍 teask 直接就可以拿到存不存在?这是首先确定的第一个收益结构。用哈西麦布。哈西麦布存什么呢?存的 k, 当然是 你这个要拿的数据吗?对吧?然后 value 存什么呢? value 首先我们先不管 value, value 这个先待定,然后再考虑第二个事情。我们刚才说了, 嗯,第二个操作是 get c 对不对? get c 我要把 c 挪到末尾,我把 c 挪到末尾的时候,那 b 和 d 是不是他们要连接在一起呢?对吧?那这个时候就涉及到一个链表的结构,链表的结构。我到底是用单链表还是双链表呢?如果我用了单链表,我把 c 挪到末尾的时候,我怎么能让 b 和的 去?就是我怎么才能让 b 去连接到 d 呢?如果是单列表,那肯定是 b 有一条线指向 c 吗?然后 c 有一条线指向 d 吗?如果我 c 跑出去了,我是不能够去让 c 找到 b, 然后再让 b 连到 d 的,他是不支持这个操作的。 那怎么才能制止这个操作呢?那叫双向列表吗?也就是我 c, 我既有一条指针往前指,我可以让他找到 b, 我同时也有一条指针指向后边,指向低。就是我要挪出去的时候,我通过两个指针找到了我的前面和后边,然后我让这两个连接起来之后,那我就可以跑了吗?我就可以跑到最后了,我就去调整我的指针了。 当然这个 b 也有一条指针指向 c, 然后第一也有往前的指针指向 c 吗?对吧?双向列表通过这个结构就可以把这个 c 挪到末尾,进而让它相邻的两个节点能够连接在一起。这就是第二个数据结构。双向列表。 对这两个数据结构确定之后,那就要想一下该怎么扣顶,就是扣顶的细节。 另外这个双项链表对吧?这个这是一个一个的节点呀,这是一个一个的对象对不对?一个一个的对象。那我们就要组织一个 no 的节点。 no 的对象。 no 的对象他肯定有一个 k 吗?然后有一个 v 吗?然后有一个 嗯,一个普瑞指针对吧?然后有一个嗯 nax 的指针。两个指针以及他的直,以及以及他的 k 和 w 的直是什么?也就包括两个指针。这就是这个 no 的他这个对象他的一些属性。 然后我们哈西麦普存什么呢?我们刚才这个 v 还没有确定对不对。微存什么。那我当然是通过当时候,到时候我去哈西麦普去判断什么呢?哈西麦普的作用就是你给我一个你要拿的 k, 我去通过 get 去哈西麦普里边去,肯定是 k 去判断他 存不存在,如果他存在了呢?如果存在了,那我要 get 的时候我要返回什么呢?我要返回的是他的 value 对不对? 而这个 v 六是在这个 no 的里边包着的,所以我这里面要存一个 no 的对象,也就是这个 k 对应的 no 的对象。我拿到 no 的对象之后,相当于我就通过你的 k, 我定位到了 某一个 no 的结点,就是双向链表中间的一个元素,我通过这个元素我就可以调整我的左右指针,以及我把它挪到末尾啊之类的,这些都可以操作了, 对吧?这就是整个的一个数据结构的选择,以及我要用哪些对象去把这些属性给包起来,他的一个流程。然后我们看一下代码,代码还是有一些 自己需要注意的。首先这个 likt 就是我的一个自己实现的 lkt 的类,这个 kitty 它包含两个元,两个数据结构吗?一个数据结构是什么?就我们刚才说的哈西麦破 hi map, 它里边它的一个 k 就是你的,这里边是发型啊,就是 k。 然后你的就是这里边的一个 no 的里面的它的 k 的直,然后歪了呢,就是一个个的 no 的。首先我们看一下这个 no 的 那个里边有四个元素,四个属性,就是刚才说的一个 k, 一个 value, 一个普瑞,一个 next, 两个指针。 还有一个数据结构就是双向列表。这里边我们自己实现了一个双向列表。而没有用 link 的历史者。为什么没有用 link 的历史者呢? 因为另个类似的他这个数据结构你没有办法说你直接去抓到他的头和他的尾。而我们这里呢?因为我们要调到尾部吗?所以我们 不通过这种便利的方式去跳到尾部,而是通过这个我们自己实现的 double link list。 list 这里边有两个属性,一个是黑暗的和一个 tell, 就是他的头和他的尾,我们直接就通过这个指针拿到了这个尾部的元素, 以及这个害的拿到他头部的元素,这样就不用通过这个链表,你去一个一个的去便利,便利到尾部才能拿到尾部。去调整。 就是我们在这个过程中,我们自己去抓住这两个属性,然后在这个过程中我们自己去调整。对,这就是这个结构。 那我们再详细看一下吧。详细看一下这个结构。这个结构 w 的历史的。这里边两个属性,两个属性对应了两个方法。这两个方法呢?就是三个方法,一个是把一个节点挪到尾部, 挪到尾部,就是在这个链表里边把一个节点挪到尾部。还有一个就是我 把一个新的节点插到这个列表双向列表里,那肯定是插到尾部的吗?对吧。 然后就是我把头部的元素给移除,为什么移除呢?因为我当我的容量不够的时候,我剔除的时候,我就剔除头部元素,其他的都不用考虑。就是这三个方法。这三个方法是在你在用我的这个 lio can 的时候,他的某些方法时候会掉你的。这个我们自己写的这个双向列表结构,去调整,这个双向列表结构里边的元素,以及他的一个指针, 就是这个类。然后有一个容量,我们偶尔要开启,你在处置化的时候肯定要给他一个容量,你的容量大小是什么?就是你这个容量限制住你超了我就要剔除。是这个意思。当然这这边给了一个,嗯, 给了一个高端方法。高端方法呢?给定容量,那我们就把这两个输结构处置化,然后把这个容量给指定好,然后关键的两个方法来了,一个盖的,一个铺的。这就是我这个 cat 对外提供的功能。外边只知道去盖的 去铺的,他不关心我里边的这个链表结构是怎么调整的,也不关心你到底怎么剔除的,这都是在这个过程中我们自己实现的功能。 首先看一下我要你给我一个 k, 我要去我这个 cat 里面拿这个 k 的对应的 value 的时候,我首先要判断一下你这个 k 在不在我这个结构里。 我们刚才对应了两个结构对不对?我们这个哈西半部就是做这一部判断的,哈西半部看他存不存在这个 k, 如果不存在,那说明我这结构里也没有,我就返回空。 那接下来就是你存在吗?你存在,那说明我可以通过这个哈西麦普拿到你这个可以对应的 no 的。 我拿到了这个 no 的之后呢,就像我们刚才说的,我去访问 c 的时候, c 原来在这,我要去访问他,访问他的时候他就要挪到末尾。挪到末尾的时候,我要调整 b 和 d, 让 b 和 d 去连接起来,然后 c 再跑到末尾。 那这样对应的一个意思什么呢?就是我要去这个双向列表里边去调整你的结构,以及把你的你给定的这个 no 的移到末尾。移到末尾首先看一下怎么移。首先你如果 我这边抓到了一个末尾的值,如果这个末尾的值就是你的这个末尾。比如说刚才你这个 abcd 一对吧,你破了进来一个一,然后你立马就 get 这个一,你去 get 这个一的时候,你这个一本来就在末尾吗?我也没有必要再去挪动他了。所以你如果这个 q 等于这个 no 的时候,那我就返回不用挪动。否则的话,如果这个 head 等于这个 node, head 是什么? head 是头部的结点。如果等于这个 no 的, 那说明这个黑暗的他只需要把这个头部去挪到尾部,对不对?那这个时候为什么要把这种情况独立起来呢?因为你的黑暗的,你前面指向的指针是空, 你不需要去调整你的 head 的普瑞,然后你让 head 的普瑞指向他。没有必要做这个操作。 但是你这个元素在中间就不一样了。你看我们这个衣服又是一个,又衣服又是衣服,一个又是三种情况。就是在尾部的时候,你弄的在尾部,我不调整,你弄的在头部,那我只调整你只你后边的指向, 以及你后边指向,指向你的那个什么,以及你的孩子的变成 b, 对吧?是这种操作, 这种情。这种情况是什么呢?这种情况就是 c, 这种情况他在中间,那他调整的指针就要多一点。这三种情况给分割开了。这个时候首先看一下,当这个 no 的是 head 的时候,那首先我要让这个 no 的下一个指针的普瑞。原先比如说 b 原先指向是 a 的,现在我让他指向空。 然后呢,我这个黑暗的原先这个指针指向的是这个 no 的节点对应的那个内存地址。 现在我要让这个 hit 指针指向原先的这个 a 的, nex 的,就是 hit 的 nax 的指针, headnancy 的指针指向的那个啊, no 的 的内存地址。我让他指向他,就是害的变变变成 b 了,从 a 变成 b 了,那这个时候这头部就调整完了。然后就就要调整这个尾部了。尾部首先原先是个 q, 现在原先的老 q 老尾部 then next 变成这个心动的。 然后这个新这个新的一个 note 的前一个指针指向跳,就是 d 和 a, 它进行一个双向指针的变化,就是我指向你,你指向我。然后呢?然后我让我这个 no 的 新的 note 的 nax 的指向空,因为我的 nax 原先是指向 b 的嘛,我现在的 nax 要指向空,因为我变成尾部了。最后再把这个跳指针,也就是我们自己维持的两个指针指向头部和尾部,就是这边指向尾部的这个指针指向我的这个 no 的, 也就是你的心尾部。就是这种情况。还有一种情况是什么?第三种情况就是 c 这种情况, c 这种情况我要调整指针 这个这个这个这个,以及 b 指向 d 的,还有尾部的一和 c 他之间的一个指针。首先看一下我 no 的的原先这个 c 的 no 的前一个指针的 next 指向我弄的的 next, 也就是 b 指向地。 接下来我这个 d 就是 not 的 nans 的他的一个向前的指针指向 note 的前一个指针指向的地址,也就是 d 指向 b。 他俩的完成了一个指向的调整。接下来呢,这个 c 要来到尾部了。来到尾部之后, 我要让我原先的跳的 nice 的指向弄的,然后我弄的的前面那个指针指向跳,就是他俩的一个双 方向又调整完了。接下来呢,我这个 no 的的 nice 的原先是指向地的,现在我要让他指向空。最后我把这个 q 自己维持的抓住指向跳指向弄的。这就是把一个弄的 移动到尾部的他的一个过程。 移到尾部之后呢,那返回的是什么返回的,其实我麦克里边就已经拿到这个 no 的了,我直接把这个 no 的的 value 返回就可以了。其实这一步都是在调整双项链表, 如果直返回直的话,其实不需要这一步,这一步就是在调整双向列表的结构,就是这个 get 的方法。然后再看一下更麻烦的铺的方法。铺的方法给定一个 k, 给定一个 w。 首先我要看你 要普特的数据,就是这个 k 在不在我这结构里,就是如果你在这个结构里,那说明是一个直的替换吗?对吧?我没有必要去添加一个新的元素在末尾, 比如说这里面你存在这个 k, 那我就把你这个 k 的 w 变成你的新 w, 就是相当于值得覆盖。值得覆盖完了之后呢,我再把这个双线练表 里边的这个 no 的移动到末尾。因为刚才我们也说了,不管你是破的破的方式,还是掉破的方法,还是掉 get 的方法,你只要触发到了这个 no 的,那这个 no 的就要移动到末尾。这个结构就是要调整这个 no 的 他的在这个双向列表里面的结构这边把它挪到末尾。刚才我们已经过过这个流程了。对接下来呢,如果这个 结构里面你不存在这个 k 呢,说明你是一个新的弄的,新的弄的进来的时候,他有可能出发淘汰。就是你的容量充不充足。首先我要判断你当前的容量是不是已经达到给定容量值了对吧?如果这个时候你达到了,那说明我要淘汰的,我要淘汰一个元素出去的。 我淘汰完了之后,我再去把你这个 no 的去加进来,加到我的麦克里边,也加到我的双向列表里。首先我们看一下这个淘汰的过程,怎么淘汰?淘汰?我们刚才说了,淘汰肯定是淘汰投机点,因为投机点它离时间线最远, 就是离最新访问的那个点最远,就是他最古老。首先看一下这个 remove head 什么逻辑?首先如果 hea 的等于空的话,说明这个双列表 什么结果都没有吗?我就返回空。然后如果你这个黑的,你是黑的和跳箱等说明什么?说明你这个双向列表里面只有一个元素, hit 和跳指向的都是一个东西,只有一个节点。那这个时候呢,我只需要把这个元素删掉就可以了。怎么把这个元素删掉呢?也就是 hit 不指向他,跳也不指向他,都指向空,那那个元素就自动删除了对吧?自动回收。 这是双向列表里面只有一个元素的时候。然后是双向列表里边有至少两个元素的时候。该怎么去调整?怎么把头部给移出?头部移出。首先我这个头部, 我这个头部我我首先这边用一个,用一个指针先抓住你的老头部的指向,老老黑的指针指向的一个内存地址吗?就是老头部老头部。然后我把我的黑的指针指向我的新头部。新头部是什么?就是你老头部的下一个节点。 这是黑的指针调整完了,就是我们自己维护的那个黑的指针调整完了,黑的指针调整完了之后呢?我老的黑的原先是有 他的一个 nikes 的是指向谁的?老的黑的。比如说老的黑的是 a, 他的原先的 nikes 的是指向 b 的。那我现在要把原先的这个 nic 指人指向空,因为我要把 a 给完全移除掉嘛,他已经移除了。那他指向这个 b 的节点。呃,指针也要移除。就是 他要要充分的,没有任何对其他有影响的去移除掉。这是老孩子的 nice 的指向空。然后呢,我这个新的开的他的普瑞指针原先是指向 a 的,也要他让他指向空。 这就调整完了。调整完之后,这个黑暗的指针指向的就是 b, 就是维维,他维持的就是最新的这个头部,他的内存地址。 这是调整完了。调整完之后,我要把什么返回呢?我要把老头部返回我这边 remove head, 他返回的是被移除的那个 head 的。弄的是谁?对,就是这个方法, 我把这个老的 no 的移除了。如果你老的 no 的不等于空呢,那我就要把你的老 no 的对应的 k 对吧,在你这个 哈西半普里边给你删掉。就是我不只要把你从双向列表里面删掉,我同样要把你从哈西半普里边删掉。这删完了。删完之后, 那现在容量充足了吗?就是相当于我删一个,我还有一个容量。那这个时候我就要把一个新的弄的加进来,新的加进来的时候,又一个弄的,又一个弄的。之后我把我的 k v p 的到我的麦弗里, 然后我再把我的这个新的 no 的加到我的双向链表里。一个新元素加双面双向链表,那肯定是加在末尾对吧?我刚才也说了加在末尾,怎么加在末尾呢?如果这个方法是为了严谨啊,如果你的这个 no 的等于空, 是直接返回的。当然这个调这个方法的前提是什么?是你前面调他之前, 你已经确定这个结构里面已经没有这个 no 的对吧?没有重复的那个就是 k 肯定不存在才能去调。这个方法就需要前面调他的时候去保证 这边就假如他已经保证了,那这个时候就 no 的等于公我为退。然后呢?我要把 no 的给加进来的时候,他因为他设计他双向列表,他涉及到双向他指针的调整对吧?如果你这个 双眼列表里面一个元素都没有,那就是黑的等于空的时候,那这个时候我只需要把我的黑的和 thale 指向你就可以了, 就不需要调整什么指针了。其他的那些向前指向的,向右指向的不需要调整。但是其他情况就是这种除了只有一个元素的,除了一个元素都没有的情况,那说明至少有一个元素吗?那这个时候我 我就要去调整指针了,比如说原来只有哎,那我现在要加一个币的时候,那相当于我原先跳指针的 nice 的。 就是我在原先尾部里边,我加了一个新的元素进来, to the next 指向 no 的,然后 no 的普瑞指向 to, 就是双向维持调整好了,然后我让我这个跳指向我这个心的 no 的,这样就把这个新元素加进来了。就是这个方法。 新元素加进来了之后,其实那这个过程就结束了吗?所有的过程,所有的流程都已经结束了。这是这个铺的方法。 这就这个自己时间的 aok。 然后我们运行一下,先加 abc, 然后再盖的 b, 那这个时候正常情况下是二吗? 然后这个时候正常情况下是什么?正常情况下是一。这个时候因为给定的 catch 的容量是三,那加 abc 的时候容量已经满了,再加第的时候,那说明他会触触发一个淘汰。 淘汰的时候,因为我们刚才先加了 a, 再加了 b, 再加了 c, 其实就相当于这个情况。然后呢?然后我们又 get 了 b, 然后又 get 了 a, 那现在情况就是听一下,咱们换一下这个。 一开始我掉了 a, 掉了,我扑到 a, 扑到 b, 扑到 c, 然后我又 get 了 b, 那这个时候又变成了什么? 又变成了 acb 对吧?必要来到后边。接下来我又 get 了 a, 那说明我 a 要 来到后边,那就盖变成了 cba 对吧?然后我去把 d 铺的的时候,你会发现容量已经满了,那这个时候我要淘汰一个,那就相当于把 c 给淘汰, 然后滴进来变成 b, a, d 对吧?这个这个时候我再去 get d 的时候,滴,刚才他的值是什么?值是四吗?然后我再去 get c 的时候, c 因为已经被淘汰了,他就不存在了对吧? 这个是四,这个是空,对吧?所以最后输出的就二一四空。我们看一下运行一下 对吧?这就是这个自己实现 iosk。 这是一个中等难度的旅客算法原题。
 02:41查看AI文稿AI文稿
02:41查看AI文稿AI文稿了解过 redis 中的内存淘汰算法的同学,对于 l r u 和 l f u 这两种算法一定不陌生,可是 l r u 和 l f u 的本质区别是什么?如何从深层次去理解内存淘汰算法的底层逻辑? hello, 大家好,我是箍炮科技联合创始人 mike, 今天我将会分享一下 liu 和 lfu 算法的实现原理,去帮助大家提高价格设计思维。另外,我把往期的视频内容整理成了一本家网面试指南,里面包含了五十万字的面试文档、两百份精修简历模板以及家网价格师学习路线图,有需要的小伙伴可以在我的评论区置顶中去领取。 l r u 和 l f u 都是内存淘汰算法,这两个算法的主要作用都是确保在有线内存中存储的数据尽可能都是高频的,也就是所谓的热数据。以 redis 为例, redis 中的数据呢,是存在内存中的,一旦内存不够的时候, redis 会淘汰部分不经常使用的数据,腾出内存空间,这里就会用到内存淘汰算法。尽管 l i u 和 l f 的目标相同,但是他们的工作原理和决策过程是有本质上区别的。第一, l i u 算法呢,一般是通过一个链表加哈气表来实现的,双向链表用来记录节点的顺序, 头部表示最近访问节点。哈奇表呢,用来提高列表的数据查找速度。当访问某个数据的时候呢,我们会把这个数据移动到列表的头部,表示热点数据。如果列表的长度达到预值,我们会把尾部的最后一个节点去掉,这就是淘汰过程。 可以看到, l i u 的原理是基于一个假设,也就是最近使用过的数据在未来再次被使用的概率比较高,他会跟踪每个数据最后访问的一个时间,并淘汰最长时间没有被访问的数据。所以呢, l i u 有一个弊端,就是如果某个数据长时间没有被访问, 但是最近被访问了一次,他有可能被定性为热点数据。第二, l f u 算法一般是采用多个列表来组合实现。 l f u 的实现通常需要一个计数器来记录每个数据项的访问次数。他的基本思路是会记住每一个数据的访问频率,并且按照频率进行排序, 一旦缓存满了,则会淘汰频率最低的数据。 l f u 算法基于另外一个假设,也就是过去频繁访问的数据在未来也可能会被频繁访问到。 当长期数据访问模式比较稳定且重视数据项的频率更多于实效性的话, l f u 是一个最适合的选择。 这两种算法各有优缺点,适用于不同的应用场景。 li 的实现通常更简单,而 lf 呢,可能需要更复杂的数据结构来高效跟踪和更新访问频率。在选择缓存淘汰策略的时候呢,更重要的是要考虑你的应用场景和数据访问的一个模式。 以上就是我的理解,今天的视频呢,就分享这里,如果你觉得这个视频对你有所帮助,记得点赞和关注,我是麦克,我们下期再见。
 02:05查看AI文稿AI文稿
02:05查看AI文稿AI文稿red is the lru 算法是如何工作的? red is 中的 lol is recently used 算法是一种用于管理内存中数据的算法。它的主要目标是在内存不足时选择要删除的数据项, 以便为新数据腾出空间。 l r u 算法基于一个简单的原则,最近最少使用的数据项将被优先删除。 以下是 redis 的 l r u 算法工作原理的详细解释。一、数据项访问当一个数据项被访问、读取或写入时, redis 会将该数据项标记为最近使用,并将其移动到列表的前面,表示它是最新的数据。二、列表维护 redis 维护一个双向列表,或称为列表,用于记录数据项的访问顺序。列表的头部表示最近使用的数据项,而尾 不表示醉酒未使用的数据项。当一个数据项被访问时,他将被移到链表的头部。三、淘汰策略当 redis 需要释放内存以容纳新的数据时,他会从链表的尾部开始查找醉酒未使用的数据项, 然后将其删除。这就是 l r u 算法的核心。选择最久未使用的数据项进行淘汰。四、过期键处理在 l r u 算法中,如果一个数据项设置了过期时间 t t l, 那么他将根据 t t l 值自动过期,即使他曾经被访问过。过期键的处理不依赖于 l r u 算法。需要注意的是, redis 的 l r u 算法并不是精确的 l r u 实现,因为完全记录每次访问可能会导致高昂的性能开销。相反, redis 采用了一种近似 l r u 的策略,它可以有效的管理内存,同时保持相对低的计算成本。总结来说, redis 的 l r u 算法通过维护一个数据项访问顺序的链表来选择要淘汰的数据项,优先淘汰最久未使用的数据, 从而帮助管理内存并确保高效的内存使用。这使得 reddis 成为一个出色的缓存和数据存储引擎。
 08:29查看AI文稿AI文稿
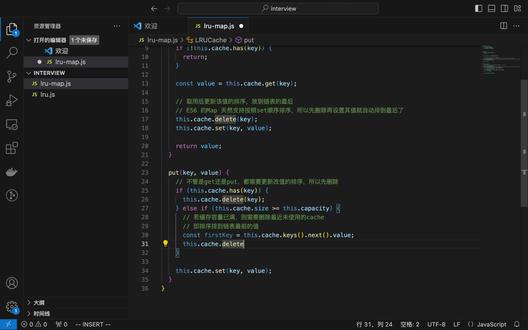
08:29查看AI文稿AI文稿今天我们来看一个手撕代码的一个题啊,就 l r u 缓存。这个缓存的话主要就是为了存储 呃,固定容量的一些缓存。这里这个这里容量只是指的那个我们缓存调数就是 最近用的缓存,可能他的优先的顺序在前面,然后用的越少的缓存,他的他的排序可能就在后面。所以我们这里用结实的一个 es 六的 map 结构来存储这个缓存。后面我们待会儿讲一下 为什么用这个 map。 要实现这个缓存的话,我们有两个方法,一个是 get 方法,一个是 pro 的方法。 get 就是取用就是取用, pro 的话就是设置我们缓存值。不管 get 还 pro, 我们都需要在每次调用的时候去更新这个缓存的排序, 就相当于最近用到了过后就必须要把它排到前面。呃,我们这里 get 的话,我们先判断一下它有没有这个值,如果没有我们就直接返回返回浪,这里应该是 on the five。 然后我们需要去把这个纸取出来,直接取出来。 好的,取出来过后,我们就需要把这个把这个值的排序更新一下。这里怎么更新呢?主要就是说 相当于把先把他之前的值先删掉,删了过后我们再去 set 一次, set 这一次过后,我们就这个值的话,就自动地 set 到我们的 map 的最后了。所以我们刚我们来说一下这个 map 结构。 map 结构的话, 嗯,理论上他就是一个有序的,就是他的 k c 有序的排序的。他的顺序主要依赖 set 的时候的一个排序, set 的越早,他的排 排序 k 的排序就越靠前,现在的越晚的话,就排序就在最后。所以我们用这个 map 的一个特性去实现这个排序。 好,我们设置了过后先删除再设置,这样的话我们用到的这个 get 这个词的话,就直自动的排到我们的最后了。 这里要注意点就是排到最后的话的意思是就是这个他被删除的可能就是在最后,因为我们删除的话是从这个。其实 这里没有列表,但是我觉得这个说一下列表就是我们删除的数是三的列表头。 当我们的缓存的容量超过我们设定的容量过后,我们直接把他的头删掉,这样的话我们的越靠后的一个缓存值就相当于越被删的可能性就越排到最后。 ok, 这就是我们的 get 方法已经实现了。我们来看看我们的 pro 方法。其实 pro 方法的话和 get 的的这个实现的原理是一样的啊,就是首先我们要判断一下有没有这个值,如果有的话我们就把它删掉, 删掉的目的就是为了更新它的排序。 然后我们就直接把这个值给 set 一次。 pro, 其实就是 set 的意思啊,把这个值 set 这样的话,它排序就放到了最后,就最后才能被删。 然后我们还要判断一下这个容量,如果当前的缓存容量 小于大于或等于我们的设定的容量的话,就需要去删除我们多余的缓存。 这里刚刚说的我们三的话是从头先上起的,所以我们需要去找第一 一个元素。 我们这里就直接去取我们最前面的一个 key, 我们这里直接用它的 keys 方法可以获取这个 map 的所有 key。 然后这里为什么有一个 next value, 是因为我们取到的 key 是一个可叠的对象,它有一个 next 方法,其实类似我们的 generator, 每掉一次 next 方法会返回一个 value 和一个 down, 释放为出和 force。 所以我们这里就直接取到了 first k, 然后我们就把这个 first 给删掉。 这就是我们的整整个 l r u 缓存实线的一个方法。我们来测试一下,就是我们这个到底有没有效。 测试的话,我们就直接在这个文件里面写一个测试方法。首先我们实力画一个 ai, 由缓存 实力化完成过后,我们传一个,它的容量为三。我们依次的设置三个 不同的 key 哦,应该是四个。 这里我们快进一点啊。 好,我们设置了四个不同的值。理论上当他超过与四过的时候,这里的话会删除最 最先插入的一个元素。因为我每次 pro 的时候,他的优先就会变更嘛,所以他应该 打印出二三四。另外我们测试一下 get 方法。 二三四。 get 方法的话,当我们有只有二三四的时候,就相当于有只有 b c d。 我们再 get 一下 b, 理论上我们的 b 的话就会排到 我们的最后的一个位置,所以说他会输出三四二的一个排序。我们在我们终端里面去测试一下这个结果。 好,大家我们可以看到和我们的预期是一致的, 我们的这里是三四二是对的,然后这边是三二三四也是对的。所以这就是我们的一个 l r u 缓存。用 e s 六的 map 怎么去具体实现啊?今天的节目就到这里,谢谢大家的观看。
 02:34查看AI文稿AI文稿
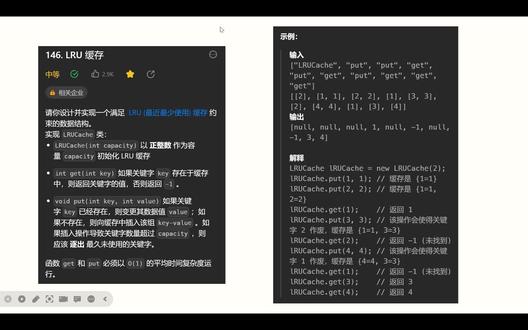
02:34查看AI文稿AI文稿大家好,这里是哲图,我们来讲一下今天的立口,每日一题, lru 缓存。这又是一道程序设计类的题目,让我们实现 lru 缓存的 get 和 pro 操作。那简单说一下 lru 缓存是什么?在我看来就是实用主义的体现,那比如说我现在需要对一些工具进行排序,如果用了下锤子, 那么我就把这个锤子从这个工具里面拿出来,用完之后,我把这个锤子放到所有工具的最前面。那如果我用了下锄头,但是工具里没有锄头,那么我从别的地方搞来锄头之后,我就把它放在所有工具的最前面,如果工具的数量超过了最大限制,那么我就把最尾巴的工具扔掉。 l r u 就是我最近使用的,就排在最前面,很久不用了,就排在后面,直到超过了容量,我们就把这种不用的移出缓存在本题中, get 操作就是要我们找出缓存中是否有目标的剑指队,如果有,那么我们需要将这个剑指队移动到 缓存的最开头,如果没有,我们直接返回负一。或者操作也需要我们找出缓存中是否有目标的限制队,如果有,那么我们更新这个键的值,并且移动到缓存的最开头,如果没有,我们就添加这个键时队到缓存的最开头。并且如果缓存的大小超过了限制的大小,我们就把缓存的最末给丢掉。并且如果缓存大小超过了最大限制, 那么我们就把缓存的最末尾的数据给丢掉。这个模拟起来其实不难,难点在于常规的模拟会超时,因为题目这边要求我们用 oe 的平均时间复杂度,也就是说我们无法通过便利缓存来实现模拟的操作。 我们需要记录缓存中的先后顺序,并且有时候需要改变先后顺序,因此我们这边是使用电表来记录缓存。如果我们要从容器中找出一个元素,但是不能通过便利的方式去找,那么比较容易想到就是用 set 或者是 map。 我们这边用的是 map, 用 map 来将键以及键值在电表中的迭代器的指针进行一个绑, 这样我们既可以定位到缓存中的目标,使用叠带器更方便我们删除列表中的节点。在 get 中,如果我们找不到,我们就返回负一,反之就把对应的键子从列表里删除,我们再添加回列表的开头,并且需要更新 map 中的记录。这边有个错误示范,我做这题的时候,这边卡了一下, 就是我们这边需要获取的是目标的剑指队,而不是获取目标的迭代器。因为如果是迭代器的话,我这边做一个三组操作之后,迭代器的位置他指的位置是不变的, 但是原本位置的元素却发生了改变,我们这边再添加回去的话,就可能不是原来的元素,而是未知元素了。所以我们这边获取的是剑指队,删除的时候我们用 map 来获取,添加回去的时候我们用这边获取出来的。在步骤中,无论我们找不找得到剑,我们都需要把新的剑指队给添加到列表的开头, 如果找得到键,我们就把键在列表中的老地方给移除掉,如果找不到呢,我们就需要做个判断,如果缓存的大小超过了大小限制,我们就需要把列表的尾部给移除,那么这里是截图,我们下次再见。
 03:20查看AI文稿AI文稿
03:20查看AI文稿AI文稿大家好,我是同龄课堂朱老师,今天来赶会,分享一节面试题, red 淘汰 k 的算法 l r u 与 l f u 的区别啊。 呃,那呃你要搞明白这个问题啊。呃,你要呃看看我们上一个面试题啊,关于那个 ready 是那个淘汰策略啊,就是内存淘汰策略,他是怎么回事啊?我们这边当时讲了八种策略啊,那其实关于这里面呃像每一种策略的区别,比方说像这两种啊,后面有个 lru 啊,这个 l f u 包括这种针对过七 k 处理的两种策略,也是 l r u l f u 啊,其实它们都是呃针对我们内存 k 淘汰的一些算法, 那 l r u 和 l f u 它们之间到底区别什么样?也就设置两种策略它有什么区别?给大家解释一下。就是 l r u, 顾名思义嘛, next recently, 就最近最少使用 用的 k 我会删掉。那然后还有一个叫 nes 的 frequently use, 就最近最不经常使用的 k 我会删掉。也就我们说的 l f u l l r u 它干嘛?它是淘汰掉很久没有被访问的数据, 注意,它的淘汰标准是以最近一次访问时间作为参考的。那 l f u 它实际上是淘汰最近一段时间被访问次数最少的数据,它是以访问次数作为参考的。 ok, 那这两种算法什么时候呃用哪一种呢?那给阿给阿豪去讲讲。其实我们绝大多数时候我们都应该用 l r u 这种策略,这种策略实际上是我们用的最多的, 那就包括这个内存淘汰策略,就我们也推荐那会呃选这种策略就针对过七 k 使用 l r u 的算法,那当然,有的同学说,那 l f u 我什么时候去用呢?是这样的啊,如果说,呃,我们的业务 场景里面是有大量的一些热点缓存数据,那我告诉你,针对这种情况,我们用 lfu 可能会更好一点。为什么?给你解释一下啊?就是比方说我们热点缓存大家都知道,那肯定访问次数是比较多的,对不对?那假设我们现在有一个热点缓存的 k, 假设 ke 他可能在五分钟之前被访问了几百次,假设访问了两百次, ok, 但是最近这五分钟可能暂时,呃,前端没有发过来请求访问他,那假设我们现在还有个 k 二,这个 k 二他可能上一次访问是几分钟之前。 那不巧,在我最近的几分钟,也就最近这五分钟之内有一个请求给他访问了一次, ok, 那大伙思考一下,我们现在说的场景是有大量的就这种热点缓存数据是比较多的,也就呃很多很多缓存他的使用次数,他的使用次数比较多的。但如果说 你用 lru 这种策略来去淘汰数据的话,那干嘛?那在这种情况下面可能就把 k 一给淘汰掉了。那 k 一是热点缓存,可能最近这五分钟确实没有被访问,但可能马上就有很多次的请求要请求到他了, 对不对?那所以你又把他删掉了,那对我们整个性能肯定会有影响。那所以对这种大量大量的这种热点缓存的场景,我们推荐大伙可以 用 lfu, 可能会更好一点。以他的那个访问次数的多少啊为淘汰的依据,可能会更好一点 啊。好,那呃今天就分享这里,那大伙如果说最近在面试的需要更多面试题的同学啊,我这边给大伙准备了很多很多。那大伙回头如果说想要啊,找一下啊,就可以去一下我们那个视频区的下方评论区获取啊。







