大家好,我是土木光头强,欢迎来到我的材料理学课,通过之前课程的讲解,已经为大家介绍完了平面英语状态分析的第一种方法解析法。本次课呢,将就两个主要的基本概念给大家进行讲解,一个是主平面,一个是主应力, 那对应于这样一个复杂的应力状态的时候,主应力和主平面呢,他是判断这个材料是否破坏以及呢破坏走向趋势的一个主要的这样一个因素。因此呢,对于这两个概念,本次课呢为大家做一个简单介绍。 那通过之前的这样一个解析法的分析,我们知道这样的一个单元体上,某一个方向面上,在这里边再强调一遍,那它所对应的是某一个方向面上的这样一个硬力状态,那它并不一定是对应的特定位置的啊,那么比如说这样一系列的跟这个面 像平行的线,哎,只要他的外法像都是这样一个 n, 像他的对应的这样一个洁面上的应力状态都是一样的啊,那之前的这样一个解析法,我们知道他在这样一个某一个斜洁面上的法像应力和切向应力公式,嗯,我们从这个公式呢就到了, 那我们来观察一下这公式啊,那对应的这里边的 cgmxcgmy 以及套 x 呢,都是从这样一个单元体上已知的得出来的这样一个结论。而变化的量呢,就是这样一个角度,也就是这个面的方向角,那可以看出 斜切面的法相应力和切线应力呢,他都是与这样一个方向角变化的这样一个这样一个单指函数,那这样一个单指函数,那如果说我把上边的这样一个法向应力,法向应力,对的这样一个方位角,哎,这样一个方 方向角进行求导的话,哎,进行求导的话,那第一项呢?作为这样一个长数求导是零,那么这一项求导呢?应该等于是这个负的二倍的散音阿尔法,对吧?那二倍的跟这个月调了,那么得出来结果呢?就是这一项你都这一项, 而这一项那个球积分呢?那个套 x 提出来,那他有二倍的头散眼二发,那相应的对应的是, 那我们观察一下这样的一个式子,是否跟这样的一个式子,它的形式是不是非常相似啊?差的什么?是不是差了一个二倍的关系,对不对?二倍的关系,那一般的情况下,在数学里边,我们对一个函数如果求倒的话, 意味着什么?是不是意味着我要找这样一个函数的及时啊?对不对?哎?那么根据这两个试试一对。比,如果说对应的这样一个某一个方 角,当他转过这样的一个方位角的时候,转过这样的一个方位角的时候,恰好使刚才我们求导出来的这样一个导数值导数的这样一个式子,他等于零的话,那么这两个式子还差了一个二倍的关系,那么这二倍呢?当然跟这边零约掉,有没有没有这样一个效果了哈?是不是这样的一个 这样一个法向应力的倒数,如果等于零的话,是不是恰好也使这样一个斜斜面上的他的切应力为零, 哎,他的千里为零,那我们就把这样的一个方位,这个角,哎,方向面的这个角来称之为这样一个主平面的位置, 那么对应于主平面位置,他上面的七元力是不是等于零了,对不对?七元力等于零了,那至于说这样的一个主平面的加一个方向到底等于多少?我们就可以让这样一个试试。他等于零,哎,让 这样一个那个清理公式呢?他这样一个等于零,哎,等于零,那等于零的话,我们就能得出这里边角度这些关系,那这个呢?是主平面角的这样的一个 计算公式,这个又出来的一个公式啊,他等于负的二倍的套 x 减比上十一个八 x 减去 c 八完,哎,那这个呢?就是主平面的方位角公式,那直到这样方位角公式,哎,根据这样的一个角,我再把这个角度啊求出来, 哎,这不简单,就三角函数吗?对不对?通过一个反三角函数求出这样的一个角,那么对应于这样一个平面来说,哎,对上这样一个主平面来说,他所对应的这样一个一个角度呢,应该是有两个,因为你比球零到三百六十度求弹径值的话,哎,他会有两个角度啊,两个角度就是二三零有两个。那把这个 阿发零带入到这样的一个法性盈利这样的公式里边,哎,法性盈利公式里边,因为满足这样的一个式的时候,是不是这个函数的导数是零,对不对?那么函数的导数是零,把这样的一个 这样一个变量再带回圆方程的话,是不是根据数学里边得出来的?是这样一个法相用力打即直, 对不对?哎,等于发现了几只,那么这两个几指呢?我们就称之为它是主应力,改成了主应力,由于对应的是两个角,分别对应了一个是极大值,一个是极小值,那这个呢,就是求出来的这样一个 法向应力,在主平面情况下所对应的这样一个集值公式。哎,这样一个集值公式,我们把这样的一个法向应力的集值成为的就是主应力,那成为的就是主应力。那以上呢,就是非常重要的两个 概念,一个是主平面的概念,一个是盈利的概念。那简单的总结一下,什么是主平面,也就是说,当这个某一个方向面的方向角转入到某一个角度时,恰好使这个面上的切硬力为零了。哎,那也就是说 主平面上的切音力是要为零的,恰好使这个节节面的切音力为零了,那么对应的那个平面就是主平面,而这个时候主平面上所对应的法向应力,他的就是主应力啊,就是主应力,那他的主平面呢?当然是有两个的,是吧?有两个,我现在标出来一个哈,那个呢, 跟他是这样长一个九十度关系,因为零到三百六十度之间,这样一个对应的角度值,他俩应该是这样一个相差一百八十度,然后在这个, 因为这还有个二倍吗?这还有个二倍,那么所以它是相差九十度的关系啊。后续呢,我会通过一个典型的立体帮大家进一步来理解,本次课呢就为大家介绍到这里,更多精彩内容敬请关注土木光头强。
粉丝5527获赞1.9万
相关视频
 03:55查看AI文稿AI文稿
03:55查看AI文稿AI文稿我是你们的学长啊,最近在给很多同学上课的时候,发现一个情况,就是很多同学他不会求主引力,然后他又背不住公式啊,这种情况怎么办呢?今天的话,我们就教三分钟时间,教大家快速求出主引力,不用背公式啊,不用背公式。 我们来看这个题,他给了我们这样一个盈利状态,要求我们求出他的一个主盈利啊,怎么办呢? 我们通过以下三个步骤解决啊。第一步的话,根据他给的应力状态写出两个面的一个应力状态元的啊,应力状态上的一个坐标,然后粗略的把我们应力元给画出来啊。 第二步的话,就根据我们画的引力源求出我们的圆形坐标以及半径的大小。最后一步的话,就是根据几何关系 求出我们几个主音里的大小啊,我们一起来动笔算一算。 好,首先是这样的这样一个引力状态,我们来写坐标,我们先看 a 面, a 面的话,它是设到一个三十兆帕的一个拉力,以及一个顺时针方向的二十兆帕的一个剪切牵引力,那我们可以写写出来它是三十的二十,对吧? 前一例是顺时针,所以是正的二十。我们再看 b 面, b 面的话,他只给了我们的一个,他只给了我们一个呃,受压的一个力的大小是二十多,但是根据减一力负的经历,我们可以推知 他的这个简易力的话也是二十招霸,对吧?但是他的简易力是逆时针方向,他是简易力,是负的,然后他的那个呃正义力也是负的,所以他是负二十的负二 啊,他的坐标写出来之后,我们就根据这个坐标就是粗略的画出我们这样的一个阴历元,我们来画一下,这是 这是我们画的一个引力圆的一个坐标啊,连出来给他连起来啊,然后根据我们画的这样一个坐标的话,实际上我们可以很容易的求出我们的圆形坐标, 我们圆形的 x 坐标等于二分之 x 一加 x 二啊,算出来等于五,我们的 y 坐标呢, y 坐标也是等于二分之一 y 一加 y 二,所以算出来等于零,圆形坐标就是五零 半径呢,半径是根据我们的勾股定律过来,是吧?这里是三十,这里是五,那就是三十减五的平方,加上这么二十的平方,二十减零的平方,然后最后算出的结果是三十二点零一啊, 得到这个好,我们算把这关键的这两个指标算出来之后啊,我们再把我们的 几何,我们的第一主意力和第三主意力的一个几何信息画出来啊,从这个图上我们可以看出哈,我们的第一主意力等于什么?等于我们的圆心 x 坐标,再加上我们的半径值,对吧?然后我们第三主意力的一个长度呢,等于我们的半径减去我们圆心的一个 x 坐标。 好,那那接下来的事情就很简单了,我们把代金去算,对吧?我们第一组引力就等于我们的 圆心的 x 坐标,加上我们的半径啊,算出来等于三十七点零一,对吧?这个要再加绝对值,因为它算的是一个长度。第三组阴历呢,等于三十二点零一,就是半径减去我们的圆心 x 坐标五啊,那二十七点 也是在总也是加绝对值是吧?然后我们再一看啊,这个第三主意呢,应该是负的。第一主意呢,肯定是正的是吧,第二主意呢,就等于零是吧?那就可以直接写出来啊,这个题就这么结束了, 前后不需要三三分钟不到啊,所以说这种题还是比较简单的,大家不要担心啊啊!大家如果觉得有用的话,欢迎大家给我收藏点赞评论啊!如果说有什么想看的那种的话,欢迎私信催更, 学长可是非常充分的,欢迎大家关注一波啊!
514评论区主理人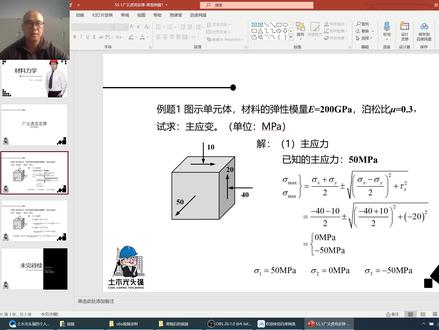 04:17查看AI文稿AI文稿
04:17查看AI文稿AI文稿大家好,我是土木光头强,欢迎来到我的材料理学课,本次课通过典型例题就广义回定率和涉及到的计算为大家进行一个详细的讲解。 那对应于这样的一个已知的单元体,材质的弹性模量呢是两百吉帕,材料的补充比呢是零点三。然后呢,要求一下对应于这样一个单元体,它的主应变是多少。 既然提到主营店,大家要涉及到想到,哎,用到的就是这样一个广益合金率,那依据广义合同率,要想求主营店,必须要知道这个单元体的主营利。因此呢,第一步我们要先求一下这样的一个单元体,他的主营利的这样一个计算, 那所设计到的相关内容呢?之前的课程的例题呢,也给大家进行讲解,在这里边呢,就简单的给大家说一下,拿过来一个单体,先看一下 他没有清理的那个面上的法相应力,就是已知的那个主应力,那单元体上前面他是没有清理的,因此呢,这样一个沿着洁面指向外侧的这个五十兆帕的这样一个应力呢,就是他那个已知的主应力。 然后依据右侧面和上侧面他的这样一个状态,再带入到平面一个状态,分析里边的这个主用力公式,哎,我们就可以求出 由 x 面和 y 面所对应的这个主营力的这样一个词,那简单的写一下,这里边 x 面它所对应的这样一个 c 个 m x 就等于负的四十兆帕,而这样一个 c 个 m y 呢,就等于负的十兆帕,而这样一个切形力, 哎靠 x 呢,在这里边就是负的二十找他。那大家在进行计算的时候,计算之前,哎一定要先把这个 你知道这样一个条件,要从图中哎读数清楚啊,要特别是他的一个符号问题,哎,符号问题,因为大小呢从图中好好找,只不过这样符号大家要会判断,如果说实在是不会的话,大家这参照一下之前的相应的视频呢,来看一下如何来确定他的这样一个符号。 把这些结果都带到这公式里边,就会求得出他的两个主用力,一个是零,一个是辅食,然后在于这个之前的这个已知的主用力进行这样一个对比,那么最大的就是这个正的五十兆帕,中间呢就是这个零兆帕,哎,最小的呢就是这个负的五十兆帕, 那得出了这三个主应力之后,哎相应的带入到这个广义股货定律里边所涉及到的这样一个主应变的竞争攻势,哎,那比如说第一主应变,这里边的弹性能量, 哎就直接用一分之一,那于这个第一组应变数对应的第一个应力,哎,就是 c m 一,然后减去 miu 位的 c m 二,加上 c m 三,就是 跟这个第一主用键对应的第一个主应力放在前边,然后后边这两个扔在后边就可以了。那在这里边在进行计算的时候,大家要特别注意啊,因为题中给出的应力的单位呢是造帕,而这个弹性磨料单位是急帕,在进行计算的时候,大家要特别注意,要注意单位扩射问题, 那单位统一的话,把这个两百级帕乘以十的三次蜜给他换成什么,换成了灶帕, 哎照哈,而后边的这里边都是用这里边的数,因为这里边应力是不是都是这样一个照拍,这样的话,在计算的时候,哎,还不能出错啊,不能出错,那么第一组应力就是五十,照怕第二组应力是零,第三是负五十,待入里边计算,结果呢就是 零点三二五乘以十的负三次密,如果不进行单位换算的话,大家可能就差这样一个十的密次啊。然后这是第一个注意点,注意单位换算,第二个注意点,注意硬电,尤其是线硬电,他是没有单位的,哎,那这边呢,是没有单位的,大家特别注意啊, 那这是第一主用电,第二主用电呢?同样你将求第二主用电那所对应在括号里边第一项就是第二主用力,对不对?然后把另两个主用力放在这括号里边,然后进行相应的计算。 哎,这还可以了啊,你会发现,哎,第二组用力是零,然后呢,第三组用力和第一组用力一加,一个是负五十,一个是分五十,一加等于零,那么他的第二 主用电呢,就是零,那第三主用电呢,也带入相应的公司来电计算,注意单位换算,注意没有单位啊,那这个呢,就是简单的利用这样一个广印回定率对某一个单元体的它的主用电的求解。本次课呢,先为大家介绍到这里,更多精彩内容敬请关注屏幕光头强。
53土木光头强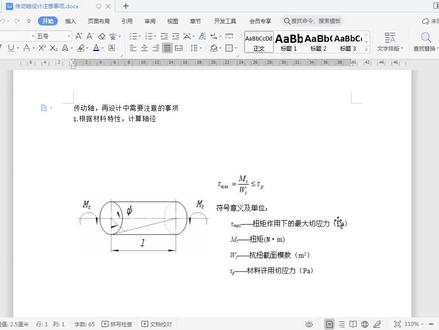 08:27
08:27 11:00查看AI文稿AI文稿
11:00查看AI文稿AI文稿大家好,我是土木光头强,欢迎来到我的材料律学课,通过之前课程的讲解,已经就平面英语状态分析问题为大家进行了详细的介绍,从本次课开始,将就空间英语状态分析为大家进行讲解。 那空间应力状态分析相对来说呢,要比平面应力状态分析要复杂的很多,途中呢,将给出了这样一个空间任意应力状态下,在一个单元体上边的这样一个应力状态。 从这样一个单元体中我们不难看出,整个这样的单元体啊,每个面上都有三个相应力,那这样的一个路面体三六一十八,总共有十八个来应力, 但是呢,根据单元体的特性成对面上的硬力呢,又是一样的,那这样一个十八个硬力呢?又砍棒,哎,变成了这样一个九个对应的这样一个硬力,再根据七零零后的硬力相互垂直面 轻盈力是一样的,也就是套歪 x 和套 xy, 套 xj 和套 zx, 套 yj 和套 jy, 那成对的,这个轻盈力是等大的,那在这样九个硬力中的,那又减去三个,那对应于这样的一个空间硬力状态,他实际上对应的独立的 变量,哎,应力变量就有六个,那什么叫做这样一个独立的,就是相互之间没有关系,哎,你玩你的,我玩我的,他们之间没有关系的,哎,那么就叫相互独立的这样的一个应力,那有六个,那即使有六个这样一个相互独立的应力,那在求解的时候也是非常复杂的, 那对应的这样一个空间任意应力状态下,他的这样一个应力状态分析将在后续的这样一个弹性力学中,这样的一个课程中为大家进行讲解。那对应于财神力学我们研究的 这样一个问题呢?不研究这么复杂的,我们只研究什么呢?只研究某一个方向面上,它的主应力是已知的。大家回想一下,什么是主应力? 比如说那个面上的他的切硬力是为零的,比如说我所取出的这个单元体,他的前后面是这个主平面的话,哎,主平面的话,也就是说前后面他是没有切硬力的,哎,那么这个时候他的前后面的这样一个法相应力,哎,这个就是我们称之为他是主应力,这样是已知的, 那对应于这样一个前面,如果他没有清理的话,比如那对应的就是这个套 jy 和套 jx 肯定就等于零了, 那如果套 jy 和套 jx 都等于零的话,那根据亲人的固定力,比如说他为零,那对应的是不是套 xj 也为零啊?那套 jy 为零,套这个这个 yj 也为零了,哎,那相对应的把它与这样一个前后面有关联的牵引力都去掉的话,哎,那这就是被我们在材料的学里边所研究的这样一个空间的相对来说简易的应对状态情况,那应对状态情况,所以大家这个不用担心,那如果说这样一个单元体 只研究这种情况,哎,那相对来说就简单的多了啊,简单的多了,那比如说这样一个,还是我们就这样一个空间应对状态分析的话,那之前说讲的平面应对状态分析的这个基本方法仍然适用,因为在三维空间中啊,他们彼此是相互独立的, 比如说这样的一个六面体的单元,他分别可以绕着这样一个红色的 j 轴来进行旋转,那绕着红色的 j 轴进行旋转,那有影响的,是不是就这样一个跑 xx, 然后是 套这个 x y 和套 y x 和套 y y, 他们之间呢?这样一个面上的应力关系呢?是围绕着这样一个这个这样一个 j 轴去到这个大圆转,那他上面的这些应力,根据平面运动的分析,比如说套 x y c m x x c m y y, 套这个 yx, 他们之间是在一个平面上的,女人的应力对不对?那他所对应的假设他的这样一个应力丸呢,对应的就是红色的,他也对应的这样一个 一个平面的应力源里边。哎,有这样的一个应力源,那同理对应于如果这个单体绕着歪轴转的话,就沿着这个蓝色的轴,那在蓝色这个绕这个这个 歪轴转,就是在这个绕着歪轴转这个蓝色这个圈转的时候呢?那他所影响的应力呢?是不就是十一个嘛? xx 和这个 套 xj 以及呢 cmajj 和套 jx, 那他们是不是在一个平面啊?对不对?那他所形成的这样一个应力园呢?他界面上的应力状态呢?又是在这样一个蓝色园上来进行变化的。而这样的一个 如果绕着 x 转的这样一个单元体的话,那他上班的,比如说 c m y y, 套 y z 和 c m z, 套 z y 是不是在黄色这个面上,对不对?黄色面上,那他所在对应的这样一个应力呢?又是对应的在这样一个黄色的这样一个圆上来进行变化, 那因此呢,对应于空间应用状态,大家不用害怕啊,所以我们不演这么复杂的,但是呢,他这样一个空间的单元体,当你绕着这三个轴分别进行旋转的时候,他上边的应用状态呀,是服从这样的一个空间的应力源的形式,那么这样的一个空间应力源还有什么 特点呢?他肯定是一个大圆套在里边两个并列的小圆的这样一个形式,然后呢鱼加一个水平轴对称的这样一个情况,因此呢,大家呢在挂空间应对缘的时候,因为虽然我们不研究这么复杂的,但是空间应对缘呢,也是这样一个材料的学历中要求大家重点掌握的这样一个 这个绘制这个应力园的这样一个方法,因此呢大家必须得会啊,就它非常简单,但是呢大家要注意啊,要注意它的这样一个基本特性,一个大圆里边偷了两个小圆,然后呢跟这个十一个马轴是对称的,那这就是一个空间的应力园。 那既然知道了空间应援,比如说这样一个单元体经过,哎,那个绕绕着这样一个三个轴来进行旋转之后呢,他肯定会转到某一个位置的时候,某个位置的时候,那对应的这个位置呢,在这个单元体上任何一个面上 都没有什么,都没有这样一个切音力,那如果这样的单音体转到这个方向的时候,哎,好了,恰巧这个单音体上切音力全为零了,那这个时候 对应面上所产生的这样一个法向应力,我们就把它称之为主应力,哎,称之为主应力,那这个呢,也就是空间的主应的概念,之前我们也讲过主应力,那那个是平面的,对不对?那这个是空间的这样一个 这个主营力的情况,那么这个空间的主营力,首先呢,这三个主营力所对应的就是空间的三个维度的方向,因此呢,这样三个主营力就是 c m 一, c m 二, c m 三,哎, 他们呢是相互垂直的,相互垂直的,那当这个单元体上面没有听力的时候,那说谁是四零八一,谁是四零八二,谁是四八三,那么他们之间呢? 哎,不看方向,只看什么呢?只看大小,哎,那对应的,如果说这个单题上清理全没有了好了,那么这个时候最大的那个主用力,我们就用 c 哥妈一来表示,而最小的那个主用力呢,就用 c 哥妈三来表示, 中间那个呢,我们就用四个码来表示,所以说主用力他们之间肯定有这样的这个一个大小关系啊,这个要分清点,分清, 那知道这三个主应力,在根据这样一个平面应力状态分析的时候,我们还知道,对应于应力力源来说,主应力是不就是这样一个应力源与 水平轴的焦点呢?对不对?哎,水平轴焦点,因此呢,刚才只是说空间应对,而让具体空间应对而怎么化,哎,我们对应于材料陆续里边所研究的,所研究的这样一个空间应对状态问题,首先是不是有一个主营力 已知的,也就是说这三个应力里边,也就这三个应力里边,哎,肯定有一个数是已知的,哎,有一个数是已知的,然后某一个方向的主应力已知,比如说好了,我先拿这个图,哎,比如说这个方向主应的已知了,那这个肯定是不是 c m 二一,就 c m 二,就 c m 三,哎,我们先不管他,那么其他的 对应的,比如说又形成了一个,就你不看这样一个在一起方向这个面的话,那么对于是不剩下的又是一个平面的应力问题,在 sy 这个面的对不对?那我是不可以根据这样一个 xy 面,根据之前的公式 又可以求出两个主用力,就这三个里边有一个数是已知的,然后根据前面的主用力公式呢,又可以算出两个数,算这三个数都得到之后呢?干什么?大小个排个,哎,大小个排个,最大的就是十个八一,中间呢就十个八,最小的十个八三,那这三个 主应力确定了。好了,在这样的一个这个应力园的这个坐标序中,哎,我分别啊,把这三个值在这样一个水平轴上来给它标出来,那当然呢,最大的就是这个 c m 一,对不对?最小的 c m 三,中间这个 c m 二 啊,那标出这三个点之后,以两两为直径,比如说有四个八一和四个八,哎,这个距离为直径会这个圆,四个八二和四个八三为直径会这个圆。然后呢再以四个八一, c m 一和 c m 三为之间会这个缘。好了,那所得到的这个单元体就是我们所研究的材料率学这部分的空间英语状态的这样一个英语员, 所以说大家碰到空间问题不用害怕,其实他还是基于我们前面简单的平面应用状态分析的这样一个结果,然后只不过加上了一个已知的某一 放上的主用力,然后来进行分析,那这个呢,就是一个空间的这个主用力,首先主用力必须会求这个空间的应力源,要去来回求 那对应于这样一个空间的应力源上。我们来看一下,当单元体在进行变,就是在这个单元体啊,空间在转动的时候,哎,在进行转动的时候,那他上面的这样一个一,这个某一个面上呢?他的应力情况呢?肯定是再加一个圆的,加你的范围之内啊,在这个圆的范围之内, 那当转到我们来看一下,对应一下,这个圆是不圆的最上边这个点,最上边点 所对应的这样一个切应力是最大的,对不对?哎?比如说圆的最上面的或者是最下边都可以哈,那么所对应的就是你不会跑出这样一个圆的范围,对不对?所以说圆的最上面点肯定是对应于这样一个单元体的它的最大的切应力的这样一个点,那 最大清理他,因为在这个最外圆的最上侧,那他的这样一个数值是不是就等于最外边这个圆的他的半径, 对不对?哎?最外边这边的半径,那最外边的直径呢?是不是由十个嘛一和十个嘛三所这样还有形成的?那因此呢,他的半径呢?就是十个嘛一减十个嘛三,然后除以二,哎,那得到了这样一个单元体上这样一个空间单元体上最大的切盈利公式,好吧,那就是 二分之四个码以间四个码三,那这个是对应的一个最主要的公式,哎,要求大家知道啊,首先对应于空间应用状态,我们不讲那么复杂的,大家要先会求他的三个主营力,然后呢依据三个主营力要会求他的这样一个空间的应援,哎,划出去三个员, 然后呢带入这样一个最大轻盈力公式,算出他的最大轻盈力。那么通常情况下对应于材料力学里边的空间,因为状态主要考察的也就是这几个内容。那本次课呢,就先为大家介绍到这里,更多精彩内容敬请关注土木光头强。
57土木光头强 16:04
16:04 00:15
00:15 15:28查看AI文稿AI文稿
15:28查看AI文稿AI文稿大家好,我是土木光头强,欢迎来到我的材料留学课,本次课具有扭转变形的这样一个洁面上的切盈力,他的这样一个由来为大家进行一个详细的讲解。 在之前的课程中呢,我们已经通过洁面法计算出了这样一个扭转时候的他的洁面上的扭距来扭距,那这样一个扭矩的效果呢?在洁面上所产生的应力效果是什么样的?我们将在这节课呢为大家进行一个详细的介绍。 首先呢,在介绍扭转切音力的之前呢,需要给大家介绍一下扭转变形的一些基本概念, 这是一个圆轴哎,受扭的这样一个变形,在外柳中容下,他将发生扭转变形,我在这样一个杆线上呢,打上这样一个纵向线以及横线线,形成这样的一系列的小格,哎, 那在外力有的作用下,这个杆线产生的扭转变形呢,会使其中的一个重象线来产生一个偏转啊,那么我们把这样一个重象线在扭转变形下所产生的这样一个偏转角,我们把它称之为,首先是 剪切角,剪切角而对应于横截面呢,在变形之前呢,比如说它的这个是它的半径,而变形之后呢,它的半径变到这个位置,而在横截面上它转过的角度呢,我们把它称之为牛转角, 这呢也是我们在扭转变形里边两个非常重要的扭转变形的概念,那扭转变形的概念,那回过头来,我们再说这样一个剪切脚, 除了这样一个重线线所发生这个偏准的角度,那这样的一个蛤蟆角呢,我们又把它称之为叫做剪切硬变,还有叫或者叫切硬变,那它的概念什么呢?是这样一个变形过程中 直角的改变量,哎,也是直角的改变量。那我们具体的通过一个立体来帮助大家理解一下,什么叫做直角的改变量。比如说,哎,这样的一个图形,变形之前呢,是这样一个黑色的这样一个框,而变形之后呢,是变成这样的红色的虚线框, 那在这样的一个变形过程中,比如说对应于这个角的位置,如果你看黑色的线的话,这个位置是一个直角,但是变形之后呢,他变成了虚线的这样一个 红色的这样一个锐角,而在这个过程中,他改变了蛤蟆脚,哎,就从原来的直角变成了这样一个锐角,那他这个过程中改变了这样的蛤蟆脚, 那么这个蛤蟆角就是意味着对于这种变形的他的这样一个切硬变。而中间这个图我们可以看一下,比如说原来是这样黑色的 框变形后呢,变成了红色的虚线框,那对应于这样的一个角的位置,原来黑色的位置是直角,但是变形之后呢,红色的这个巨型框呢,他这这个位置同样仍然是直角的关系,那在这样的一个变形过程中,他的直角并没有发生相应的改变, 并没有发生相应的改变,那这个时候呢,我们就认为他的千变视频因为他直减直角啊,没有发生改变。 那前面这两个例子大家如果理解的话,后边这个例子就比较好理解了,原来的这个位置,看黑色框的话,变形之前这个位置是直角,但是变形之后呢,变成了这样锐角,那这边呢变, 变化了蛤蟆,这边变化了蛤蟆,那相比较一下,变形后,相对于变形前整个这个直角呢,变化的角度呢是二蛤蟆,而对于这种变形,他的切音 变呢就是二嘎,就是他直角的改变量。通过这个例题,帮助大家理解一下什么叫做切硬片,以他的相应的含义,那知道了相关概念之后,接下来呢,我们就对扭转时候横截面上所产生的这样一个切硬力哎,为大家进行一个详细的讲解。 这部分内容啊,相对来说这个比较复杂哎,比较复杂,需要通过一些几何关系,物理关系以及经济学关系呢,来推导出这样一个洁面, 他在这样一个扭转时候牵引力的一个分布情况,以及呢牵引力公示。那在这个过程中呢,这个看似比较复杂,但是呢如果大家沉浸其中呢,理解呢也并不是特别困难,那并不是特别困难, 就用到的就是一些简单的几何关系啊,和一些这样一个竞力学关系。首先呢,我们来看一下这样的一个受牛的感见, 还是拿刚才这个例子,我在那个这个杆键的相邻的两个位置呢,选择这样一个两个洁面哎,然后呢把这个杆键呢给他砍开,那中间我所截取出这个段呢,假设他的这样一个距离呢是 dx, 哎, dx, 那所在这样一个截取段的外表面处呢?我选出一个这样一个敢见的一个巨型洁面,比如说 abcd, 而对应于这样一个巨型洁面呢,所对应的这样一个圆心的位置, 横即面圆形位置,我们分别用欧一和欧二来表示,哎,欧一欧二来表示,就是这个图形,是我砍开这样一个洁面之后,把中间这段给他取出来,取出来,那取出来之后,我再把这个其他不要的地方给他拿出去,哎,我只要这个 ab cd 以及呢欧一欧二所组成的这样一个先行体,乃先行体,那在扭转变形的过程中呢?哎,在扭转变形过程中,哎,原来的这样一个 abcd 变成了这样一个红色的这样的范围,比如说 adpbcp 对不对?哎,那这样一个 cc 体呢?所产生的这样一个变化, 我用红色来表示,那由于我们拿出这样一个改建呢,我们近视认为取的这样一个小这个剧情块啊,这个是非常小的,我们近视认为啊,这个 abcd 它是一个平面,所以说得到这样一个斜形体, 那我在这样的现象题中,我再选择一个于外表面就是大 abcd 这样一个平面,将平行在一个里边的这样一个小 abcd 的这样一个面,那在扭转变形过程中, 浏览和变形过程中,他所形成的这样的变形呢,就用这样一个蓝色的这样的变形来表示,而我所选的这个面的位置呢,假设他距圆心的这样的距离呢,我们用肉来表示,那用肉来表示,那相应的几何关系呢?在这样一个图形中呢,已经比较明显的给大家采取出来了, 这是第二个是,哎,对了,就是这个位置啊,就是这个位置,那根据这样的一个细型体以及他的变形关系,我们不能得到以下几个结论。首先我们看里边的这个蓝色的这样的小菌群块,哪些小菌群块?比如说这个地地铁, 这是由于扭转变形的这个地点所产生的这样一个变形量来变形量,那根据这样一个他的在 ad 地地铁,在这样的一个直角三角形中, 这样一个角度,刚才已经给大家介绍了,这叫切音变,对不对?哎,叫切音变,你说纵向线的他的这样一个改变偏转的角度叫切音变,那再这样呢? a、 d 地铁这样一个直角三角形中,这个是对应这个角的对边, 哎,直角边的对边,这个是零边,那根据三角函数关系,这样一个对边呢?等于弹进的乘以这个零边,哎,弹进的蛤蟆角乘以零边。 那在材料留学中序论中已经给大家强调过,材料留学的变形啊,都是小变形,那在这样一个小变形过程中,我们可以近视的认为这样一个 弹进的蛤蟆就等于这样一个蛤蟆这样一个角度的弧度,这个呢也是相当于数学的无胸角带换来无胸角带换,那这个 ad 呢?由于这是一个斜形体,那这个 ad 的长度呢?其实就等于这个 ds 长度,那么得到了这样一个关系,那这样一个关系,那我们这是在这样一个 ad 地铁这个平面上来进行分析,那再这样一个欧,这个欧一为圆心的这样一个横截面上来说,那从这个地地铁 说对了,这就是地范,是对扭转过程中他所这个级面所偏转的这样一个扭转角,哎,偏转的扭转角,那这个地地撇,再这样一个 右侧面的这样一个圆节面上,他相当于是个弧,那根据弧长公式,那这个地地撇,其实等于这个圆心角乘以这个半径,对不对?那这个半径呢?地欧一这个距离呢?我们可以用肉来表示,哎,可以肉来表示,那这个地地撇呢?在横截面上,右侧的横截面上,又等 于这个肉乘以这个扭转角,那把这两个柿子连粒,把这两个柿子连粒地地皮都削去了,哎,我们就会得到这样的一个柿子,哎,这样的一个柿子,那假设 左侧的这个地外,也就是说从左侧界面到右侧界面,他所转过的角度处,以这样一个他变化的这样一个距离, 那么呢,我们把它称之为单位长度扭转角,也就是相当于说从左端到右端,哎,这样的一个洁面,它所偏转或者角度呢?是地外,那再除以这段距离呢?我们就把它认为叫做单位长度扭转角,用习特来表示的话, 然后就可以把这个吉他代入到这个狮子里边,进而得到这样的一个几何关系,比如说建立了切应变,以及呢,这样一个单位长度扭转角,他们之间的关系是 什么关系?是谁的成一个肉这样一个到圆形距离的这样的一个几何关系啊?先是几何关系,那讲到这块呢,大家可能就跟我们倾力的真爱公式 有什么关系,哎,那么我先别着急,我们继续往下看。那第二个关系呢?我把第二招称之为物理关系。那么什么是物理关系?其实在力学里边所探讨的物理关系呢?就是力与变形之间的他的关系。那在材料力学中已经一再给大家强调过,材料力学所研究的物理关系呢,都是这样一个虎块定律, 那在前面已经给大家介绍了剪切时候的这样一个切形变,哎,切形变是蛤蟆,那与这个切形变所对应的这样一个切应力,哎,切形力疼,那个是成一个细数的形式,好像跟这个拉压的虎科定律是不差不多啊,哎,那么虎科定律,也就是反应说力和变形两者之间的关系。那 我们把这个剂叫做什么呢?叫做剪切磨料,剪切磨料它呢也是一个长数,是一个止于材料自身性质有关的,那至此呢,在材料律学中为大家介绍的三个止于材料自身性质有关的这样一个物理量,一个是弹性磨料,一个是薄松笔, 一个是这样的一个减轻磨量,哎,就给大家介绍完了,那这个呢,是这样一个扭转变形中的他的一个物理关系。 处理物理关系之后,我们再看一下,这是还是刚才取出的那个小切片,然后呢,这个是这样一个切片上的这样一个 c 形体来, c 形体。 现在呢,我们从右侧来看这样一个洁面的话,那在这样一个洁面里边所产生的这个扭距呢?这个梯是这样一个逆时针的,逆时针的那所对应面这个是欧一对呢,就这个位置,在这个右侧面上,这是 地点,这是地撇,哎,这是地哎,这是小地撇,是不是?哎,那在扭转过程中,他说产生了变形,哎,打字就是这样的形式,那大家一定对应好这三个图所对应的各个这个标注的这样一个符号,哎,以及对应的他的一个位置关系,位置关系, 那,那在这样的一个关系中,比如说我们取出右边的这样一个横截面,那由于扭转这样一个扭距是在这样一个结面内的,在这样一个结面内的, 那他再加一个洁面上,哎,这个扭转的平面跟洁面是一个平行的关系,因此呢,在这个洁面上所产生的硬力呢?应该是个切硬力,再加上切硬力。 比如说我在这个地点这个位置选择一个非常小的这样一个小面积,小面积我们用 da 来表示,那假设这个小面积上所产生的这个切音 力呢?是套,哎,那首先这个套要和这个扭距要有相同的转动趋势,比如说这个套如果相当于对欧一点曲距的话,也是个逆时针转动趋势,说明他是垂直于半径向下直的,而向下直的,那 把这个面积乘以这个套对应的就是这一小块 da 的这样一个面积所对应的他的一个力的效果, 那这个力的效果套乘以 da 得到了,然后再乘以到圆心欧一的距离这个肉,那他所得到的就是什么呢?就是这样的一个小面积所对应于欧一所产生的一个力距的效果,我们把它 用这样一个小地梯,哎,就是小微微扭距,哎,微扭距的这样一个含义,那微扭距的含义,那这是我们取的这样一个洁面上 非常小面积所得到的这样一个微扭距,那在这样一个圆形结面上有多少个这样小的面积?是不是有很多个呀?对不对?哎,那么把所有的这样一个小微面积所产生的这些微扭距都加起来,他所代表的这样一个数学含义,就相当于是在这样一个圆面上 所对应的一个积分,哎,一个面积分,哎,那由这样的一个念积分则所得到了建立了什么呢?就是通过净理学关系,我们就得到了扭距和级面上它的切应力,哎,所对应的一个净利学关系,哎,就是这样一个积分的关系。 那以上呢,就是我们这个扭转倾力的时候,就给大家介绍的这样一个几何关系,物理关系以及呢经历学关系。我把这三个关系所对应的这样一个公式来给他连连在一起,连连在一起 说把这蛤蟆带出来里边,然后呢对这个套再带出来这里边,然后回过头来呢,哎,经过一些代换,我们就会得到这样的一个试试,来这样一个试试,那我们通过这个试试,我们看扭转时候横截面的轻盈力跟什么有关呢?首先跟这个截面的扭距,也就是这个梯有关。 其次呢,与这样一个你所选取的这样一个点到圆心的距离也是这个肉有关。而 分母,分母这是一个什么?我们看这是一个肉是点到圆形的距离,而这样一个积分呢,是对应于一个面积积分 这样的一个数学式子,他的含义呢,完全是一个这样一个对应于跟这个洁面的形状和大学有关的这样一个量。我们把这样的一个积分的形式,哎,积分的形式就是你局面确定了,其实不管他是积分还是也好,还是什么形式也好,他都是一个长处。 我们把这样的一个积分的形式,用一个符号用 ip 来表示,这个 ip 呢叫做极惯凝聚,哎,叫做极惯凝聚啊,把这个 ip 呢 替换成这样一个这个积分的形式就得到了这样一个扭转时候即面的清理公式。 那再详细给大家说一下,这个扭转是不是轻盈力,他跟什么有关?首先跟洁面的扭距有关,跟您所选择的洁面研究点的到圆心的距离有关,以及呢与这样一个积分形式有关,这个积分的形式与这个洁面的形状和大小有关,他是一个长处,哎,他是一个长处。 那至此呢,我们就得到了扭转时候他横截面上的切盈利公式。那至于这一部分内容啊,这个相对来说呢,如果大家刚开始接触材料利水呢,可能说有点麻烦,可能听不太懂,但不要不要 着急,大家呢先简单的了解一下,最重要的还是要求大家要掌握这个最终所得到这样的结果。扭转时候及面的轻微公式是什么? 那么后续的课呢,我们会针对这样一个扭转的这样一个节目的切用力公式,哎,他的如何来进行计算以及后续的相关内容呢?给大家会进行一个详细的讲解。本次课呢,我们就为大家介绍到这里,更多精彩内容敬请关注土木光头强。
215土木光头强 02:13:30
02:13:30 16:58查看AI文稿AI文稿
16:58查看AI文稿AI文稿可以了啊,去做就可以了。好,这是这是平面的状态,一个标准的图形,标准的图形啊,就是以后呢,我们踢到平面的状态 就是这样一个图,这叫用力状态图,我们刚才给出了这个正方向了啊,给这个这个正方向了。好,然后呢我们这个做什么呢?我们的任务就是除了 就是目前是 c m s c m y 套死套外,是已知的啊,比如说呢,咱们弯曲的时候,横界面上的硬的都是已知的,然后需要求什么呢?求其他的 面上哪些面?我们前面给大家讲了,就是要找其实目的,找找那个硬的 机制,正的机制和清理机制。那么你比如说屏幕这对面没有硬的,这已经就是主平面了,这就是主平面了,我们是不是要找 你与他垂直的另外两对面?那大家想一下啊,三个面是垂直的,这个面确定了,如果我另外一个货单和他垂直的这个方位找到了,那么第三个面肯定也就知道, 对吧?因此咱们现在只需要找什么呢?与屏幕垂直的这个方向,与屏幕垂直这个方向啊?我们比如说就这个斜截面,这个面上的正盈利和轻盈就可以, 是吧?但是我们可能一下找不到他的机值,我们先找任意的面上, 我先与这个天锤方向任一个角度上的这个面的正立可亲,然后就找到这个面和阿尔法的关系了,找到这个关系以后, 然后我们再找机制就行了,咱们思路呢,就这样一个思路啊,就这样一个思路。好,那么下面呢,我们就来进行分析,咱们分析的方法上,我们是有两种分析方法啊,就是我们找任意的斜接面上的正盈利和牵引力 有两个方法,一个就是解析法,解析法还有一个呢,叫几何法,或者叫图解法,或者叫做应力元法啊,这两个方法实则是一样 样的,就一个是用解析的方法,就跟咱们那个像林立学,咱们那个讲那个,比如说平面汇交利息,我们是不是有解析的方法?也有几何法?就这个,呃,利多边形法则是吧?利多边形法则,但是我们是也可以用利多边形,是不可以求合理, 对吧?或者我们用解气的方法投影是不是也可以求合力?跟这个类似是一样的,跟这个是相似的。那么现在呢,就是我们 求任斜界面上的正力和轻力,也可以用两种方法,这两种方法都重要啊,咱们都分别介绍。好,下面呢咱们看 第一种方法啊,解戏法,解戏法。好,我们的思路是这样的,这不这个六面体吗?这个六面,这个六面体是从一个杆当中 取出来的,这个杆是平衡的,这个绿面体也得平衡。然后我现在呢,我不是求模要求某一个斜截面吗?我揭开,揭开以后就出现这个三角块,那么这个三角块呢? 他也应该是平衡的,对吧?应该是平衡的,我们就画受力图列平方程就行了。好,那我们看这个平面图啊,我们所画出来这个就是与我们黑板垂直的 与黑板垂直的这么一个面啊,这么一个面。然后呢角度阿尔法是任意的,就是与我们的,比如说与我们的 x 面相差阿尔法相差阿尔法, 那么现在就说已知条件是谁呢? c 格玛尔法, c 格玛 y, 呃, c 格玛 s, c 格玛 y, 还有 to x, toy, 然后阿尔法我任意给另一个斜接面,然后求什么呢?这个斜接面上的正盈利和切盈利,咱们这个在轴向拉压和扭转的时候都给大家讲过,只不过这个用状态简单一些。 这里规定一下阿尔法的正符号啊,阿尔法正好我们这么规定,从 x 面 外法线方向这个面的名称,看右图啊,从 s 面我们逆时针转到我们这个所分析的这个面的外法线方, 如果是逆时针就规定为正,顺着为负,所以我给出了这个 a 法,是一个正的啊,我给出这 a 法之后,你看这个面的外法线方向是这样, 对吧?从 x 逆时针转到我们这个外法线方向,我们一般是看这个锐角 啊,看锐角,那你说如果我把上面这一部分啊作为一个研究对象的话,这也可以看的是他的外法线方向啊,那我从 x 面,是吧,我可以这么转, 那这就是顺时针了,那么这个角度啊,这个角度也可以啊,你这个角度和这个角度他是有一个关系的呀,是吧,那么这就是正的了啊,那么这个,呃, 你,但是我们用锐角计算不是更方便吗?是吧?用锐角计算呢,我们更方便一些啊,好,大家明白了吧,所以说呢,这是这个规定啊,然后咱们就做什么工作呢啊,我们就求下这个斜接面上的正盈利和, 那我们就这样用用用用,用一个洁面切开,切开以后把这个三角块取出来,就是下图,但是这个图呢, 还是硬力表示的,这也叫硬力状态图?就硬力状态图,咱们是让咱们这个彩礼当中取六面体,你像有些结构呢?他不见得就是你这个单元体,不一定非得是六面体,只说我们财力学,我们是用的六面体啊, 比如说像这个水工结构当中啊,水工结构当中那个大坝,他就不是取六媒体,他是取这种三角块啊,取三角块就是他画上网格,画上网格啊,取三角块 啊这样的分析啊,所以说只要上面是用应力表示的,就叫应力状态。好,那么我们列方程哈,一定是列力的平方程,你只有力才能说平衡,你不能说应力平衡, 是吧?所以这个概念要注意你所以说这个是应力状态,咱们要把他的受力图画出来,然后针对受力图才能列平方程啊,才列平方程。好,我们看一下如何得到他的 受力图啊?咱们这么来做啊,我们的单元体都是微小的啊,那么我切开以后,你看我切开这个斜斜截面啊,你看这个斜截面,这是不是有一个面, 这个距离是很微小的,是吧?每个距离都是很微小,那你说这个面的面积是不是也属于微小的面积,是吧?我们现在就要求这个面上的正厘, 还有这个面上的切啊,我们就求这两个硬力,是吧?求这两个硬力,那么我们要换算成受力图, 我们刚刚不是讲了吗,这个面应该是很微小,所以这个面上的正盈力都认为是均匀的,每一点都是相等的,这个面上的清理每一点也认为是 相等的,那么既然是均匀的,我用这个正盈力乘上这个面的面积,是不是就是这个法线方向的力, 我再用其中一个牵引力,他不是也是均匀的吗?再乘上这个面的面积,是不是就这个面上的牵引力,对吧?这样就得到受力图了,每个面都这么做啊,好,那么现在我们就看啊,假设这个斜接面的面积是 da, 那么左边这个面的面积就是 d a 乘上 cosine 阿尔法,是吧?下面这个面积就是 d a 乘上赛尔法,对吧?然后用每个面上的两个硬力乘上相应的面积,就是 这个面所受到的力,所以说呢,这个三角块上所受到的力就跟什么呢?斜面上,斜斜面上,那么就是用 sigma 法乘上 d a, 就是发现方向力好,切线就是掏阿尔法,乘上谁呢? da 对吧?左边截面这个方是不是也有力?这个力等于谁?等于 c 个吗? x 乘上这个面的面积, 这面的面积不是 d a 口省二方,然后这个方向这不也有一个力,这个力就是掏 x, 再乘上这个面的面积就是 d a 口写阿尔法下这个面也有两个例法项的,就是 c 格曼 y 乘上这个面的面, 这个面的面积不是是用 d a 投影过来塞尔法吗?水平方向也有一个力,那就是掏 y 乘上这个面的面积,这个面的面积就是 d a 乘上塞尔法,这才叫受力 啊,这才叫受力图。好,那么现在呢,我就把这个受力图我们就换算过来了啊,换算,我就是这个受力图就这么来的,每一个面上他的力都是用那个硬力成了一个面积, 那么我们下面就可以根据这个图呢列平方程了,我们不是讲了吗? c 个吗? x 是已知的是吧? c 个吗? y 也是已知的, to x t y 都是已知的,对吧?那么阿尔法是我们任意给 的一个角度,那现在谁是未知的呢?就是 sigma alpha 和 top alpha 是未知的,只有两个未知量 是吧?二法当成变量,那么我们把这个呢,当成一个平面的汇交利息,因为这个小三角块体积很小啊,当成一个点,那么汇交利息可以列两个投影方程, 我们一般习惯列一个水平方向投影方程和外方向投影方程,但是如果列这两个方程的话, 会存在一个什么问题呢?你这个 c 马尔法和掏尔法在这两个轴上都有投影,我们需要连理方程,所以我们取一个合理的两个投影轴,取哪两个轴更合理呢? 沿着斜阶面的发线方向投影,列个投影方程,沿着斜阶面的切线方向列一个投影方程, 这样的话呢,我们两个方程当中就分别只包含了 sigma, 阿尔法和唐尔法两个方程不需要连力了 啊,两方不需要连力了,然后咱们就一个方向解一个未知数就解出来了啊,就这么一个思路上,这里回到零里学了啊。好比如投影,我们把所有的力啊,这个受力图向 n 方向投影带入和一个等于零, 所以你必须针对右边这个图,投影不能跟你左边啊,是吧?好,那么投影的话,我们先看斜截面,斜截面 只有 c 格码,阿尔法 d a, 对吧?像 n 方向投影吗?那么这个套尔法乘上 d a 就没有了,就没有了啊,然后再看左截面啊,左截面有一个 c 格码, x 乘上 d a 乘上 cosin 阿尔法,是不是在乘上一个赛于阿尔法,就是向 n 方向的投影,投影的方向呢,与我们的正方向相反,减去还有这个左截面竖方向的力,那就加上 to x 乘上 d a 乘上口省二法,这是这个力,然后再向 n 方向投影,那就乘上一个什么呢?塞啊,刚才这个是口省啊,这个是口省二法。好,这是一个塞尔法啊, 好,那么下面这个面上也有两个力,是吧?也有两个力啊,呃,有谁呢?有 c gm y 乘上 d a 塞尔法,对吧?再唱一个,塞尔法就是向恩发上投影啊,然后呢,还有水平方向力,那么加上掏掏外 d a c 阿尔法,再乘上口 c 阿尔法,平衡的话,是不是应该等于零啊?这就第一个方程,然后第二个方程像掏方向投影一样一样的啊,所以我就简单说一下,这上就理论学的知识了,是吧?好,就得到了我们这两个方程了 啊,就这么来的啊,好,其中呢,右边为零,左边这个每一项都有一个 d a 可以给他消 掉啊,下面是一样的,咱们看上面这个式子啊,那么你看,然后呢?把这个,你看这一项里头是不是有一个 cosine alpha 赛尔法, 是吧,而且我们要注意的啊,掏 s 和掏外的大小是相等的,下边看这个这一项,这一项是不是也有一个三元二法扣三二法,你把掏哎掏 s 和掏外提取出来,因为相等啊,这式子当中是不是就有一个二倍的 二倍的塞尔阿尔法乘上扣塞尔尔法,那么这一项不就是塞尔尔尔法 是吧?三幺二啊,也就利用这个三角,呃,这个函数关系啊,那么另外这个地方,我们也这个地方,我们也用三角 关系整理一下,下边也是一样的啊,整理以后啊,我们就得出来了,下边这两个是这个二阿尔法,就这么来的,我们根据三角函数关系啊,得出来,这里头有一个参数是二阿尔法 啊,是二二法。好,这个就是任意的斜接面上的正力和轻,那么我们只要给你一个角度,比如说我给他角度三十度,我带进来是不就求出了三十度方向的正力和什么呢?轻, 对吧?那么我们也可以求积值,求积值。这个我留一个问题给大家啊,比如我求正盈利的积值,正盈利的积值不就我们的主盈利吗? 而且前面咱们说了,这个主平面上气力是为零的,你们下去这样来做啊, 求一下这个正盈利的极值。怎么求正盈利的极值呢?那就是对我们的这个第一个式子,对阿尔法求解岛就是 d c 个吗?阿尔法除上一个 d 阿尔法, 然后呢?令他等于零,是不就找到那个机制点了,把这个机制点带到第二个方程里头去, 那就是说掏阿尔法零一定是等于零的,这就说明 sigma 阿尔法取得机值的时候,掏阿尔法一定是为零,也就证明了我们前面所说的啊,当正义取得 机智的时候,那个面一定没有轻易。这个咱们下去证明啊,简单的一个,这个机,这个威风关系啊,这个我们就不再多说了,但反过来啊,正轻易取得机智的时候,正力可不一定威力。所以你们这个这个问题留到下面咱们去证明啊。
344兰老师
猜你喜欢
- 2.6万王无术
最新视频
- 1539阿巾凡.





