江西切线
粉丝3.0万获赞14.6万
相关视频
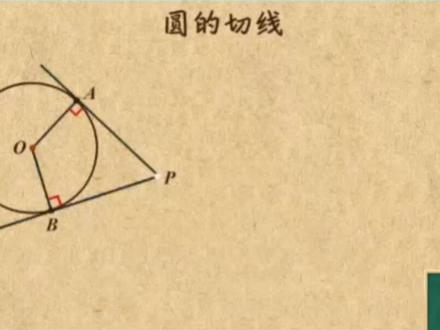
02:31查看AI文稿AI文稿这个视频咱接着来研究圆的切线，这有个圆，圆外有一点，如果从这一点出发，发现只能做两条圆的切线，那这两条切线有啥关系呢？上个视频说过，只要一看到切线，就一定要连出半径，这样切线和半径的夹角就都是九十度了。 如果再把外头这个点和圆心连起来，就恰好构成了两个直角三角形 uua 等于 obop 等于 op。 那根据全等三角形的判定定理 hl 就能得到直角三角形 apo 和直角三角形 bpo 全等，所以 pa 就等于 pb。 如果咱把点屁到切点的长度叫做切线长，那刚才的结论就变成了从一个点引出的两条切线长是相等的。同时由于这两个三角形全等，所以角 apo 也等于角 bpo， 也就是说这个点和原先的连线平分这两条切线的加角。 现在咱有了两个非常的结论，切线长相等且夹角被平分。你把这两个结论合在一起，就是所谓的切线长定理。 用了这个定理以后，再看见员外一点向圆做两条切线，就一定要想到切线长相等且夹角被平分。下面我就分别来讲讲夹角被平分和切线长相等，这两点在解决实际问题时有啥用。首先，我在这个图上添几笔，把它变成一个三角形三边都和圆相切的形式。由于这个圆在三角形内部，所以也叫三角形的内切圆。 那在这个图中，你能根据切线场景里看出些啥呢？显然，你只要连接 oq， 就会有加角被评分，如果连接 o 二，也会有加角被评分。 这么一来，原先欧其实就是三角形 pqr 三条角平分线的焦点，又因为圆欧是三角形的内切元，所以这个点也叫做三角形的内心。 由此，我们就得到了三角形中非常重要的一个结论，三角形的三条角平分线交易一点，这个点是三角形内切元的圆心，也叫三角形的内心。夹角被平分咋用你见识过了？接下来我再带你看看切线长相等该咋用。比如这个图， pa 和 pb 分 分别元欧相切于点 ab， 其中 pa 等于二， ef 则是过元欧的另一条切线，切点为 c。 请问三角形 pef 的周长是多少？相信你看条件就立马看出了 pa 和 pb 这对等长的切线，再由 pa 是二，立马可得， pb 也是二，不过还有两对等长的切线，估计你就未必看出来了。 你看 ec 和 ea 是不是也是等长的缺陷？ fb 和 fc 是不是也是等长的缺陷？所以 ec 就等于 eafc 就等于 fb。 题目要求三角形 pef 的周长，实际上你可以把 ec 翻折， ea 上， fc 转到 fb 上，那这道题就变成了求 pa 加 pb 的长度，这太简单了，那就是二加二得四，所以三角形 pef 的周长就是四。 总结一下，只要看见员外一点像圆做两条切线这样的图形，那就要想到俩切线长相等且夹角被平分，怎么样，明白了吗？如果明白，就赶紧去刷题试试吧！
97初高中数学胡老师
03:40
