全国甲卷极坐标
粉丝7.3万获赞21.2万
相关视频
 29:28
29:28 08:17查看AI文稿AI文稿
08:17查看AI文稿AI文稿哈喽,大家好,今天我们来讲一下二零二三年全国假卷的第二十题,圆锥曲线压轴题。那么这道题当时刚高考完的时候呢,我就看到有人在网上发这道题,那么我一看到这道题呢,我就立马拿来做了一遍。 首先这个第一问呢,很简单,只需要用一个弦长公式就可以做出来了,那么这个第二问呢,可以用常规方法, 我最开始就是用的常规方法来做的啊,也可以做,那么这个标准答案好像给的是这个极速标,急用极速标来做啊,其实也可以啊,极速标稍微要简单一点。 那么我们讲呢,我们就讲这个常规方法。我们先来看第一问,他要求的是 p 的值,先看题,他说直线与抛物线交于 a b 两点,而且呢, a b 这条弦长是等于四倍根号下十五的,那么读到这里,我们想到的第一思路就是把直线的方程和抛物线的方程连立,从而得到一个一元二次方程,对吧?从而通过伟达定理 以及弦长公式把 a b 表示出来,使得它等于四倍根号下十五,那么这样一个等式里面只有 p 这一个位置量,从而把 p 解出来,对吧?这个就是它的一个常规思路。所以说低问解, 我们首先要连立直线和抛物线的方程,对吧?连立 x 减二, y 加一等于零和 y 方等于二, p x 得到,那么我们应该消 x 还是消 y 呢?很显然消 i x 要方便一点,对吧?你把 x 表示出来啊,然后带在这个 po 线的方程里面就可以得到,直接得到一个一元二次方程。那如果,呃,这个如果是销 y 的话,那么你 这个叫把 y 用 x 表示出来,对吧?那把 y 用 x 表示出来之后呢?你带在这个抛物线的方程里面去,你会发现这里有一个平方,对吧?你要进行平方的运算,所以说稍微要复杂一点啊。如果我们直接把 x 用 y 表示出来,也就是 x 等于二 y 减一,把它直接带到这个方程里面去的话,你会发现这里的 x 啊,它没有平方,所以说直接带进去,然后一下下就可以得到一个一元二次方程啊,所以说这样要简单一点,我们直接消 x 就行,那么带进去你会 发现它是等于 y 方减去四 p y, 然后再加上二 p, 对吧?等于零,然后就建立了一个关于 y 的一元二次方程,那么现在我们就要来写出 这个两根之和和两根之极,对吧?首先要把这个 a b 两点把它射出来,我们射 a 为 x 一和 y 一, b 为 x 二和 y 二,对吧?那么 y 一加 y 二,注意这里是一个关于 y 的一元二次方程,所以说这里应该是 y 一加 y 二,对吧? y 一加 y 二就等于负的 a 分之 b 就等于四 p, 对吧?那么 y 一乘以 y 二,就等于 a 分之 c 就等于二 p, 对吧?那么现在我们就可以来表 表示嫌长了,对吧?根据嫌长公式,它是等于什么呢?啊?这个嫌长公式要注意有两个,有两个啊,哪两个呢?就是说如果我们这里连例方程之后,得到的是一个关于 x 的一元二次方程, 那么它对应的弦长公式就应该是根号下 k 方加一乘以根号下 x 一加 x 二的平方减去四倍的 x 一 x 二, 对吧?如果,但是呢,如果你这里连列方程之后得到的是一个关于 y 的原二字方程,那么它的形成公式和这里的形成公式就不一样了啊,哪里不一样了?这里是 k 分之一的平方加一, 然后再乘以根号下 y 一加 y 二的平方减去四倍的 y 一 y 二啊,这里一定要注意,这个是关于 x 的一元二次方程,这个是关于 y 的一元二次方程啊, 这个是他们两个的一个协商公式,这里不要搞混了,有很多同学他只知道这样一个这个协商公式,然后当他遇到关于 y 的一元二次方程的时候呢,他还用这个 公式啊,他想着可能就是,哎,把这里的 x 一加 x 二, x 一乘以 x, 分别换成 y 一加 y 二, y 一乘以 y 二,就行了吗?对吧?前面的就不管了,对吧? 那肯定是错误的啊,肯定不行的啊,根据推出来呢,实际上它是这个,它的显示公式应该是 这个,就是它是关于 y 的运二次方程的时候呢,它的协商公式应该是这个啊,所以说一定要把这两个协商公式把它记住啊,什么时候该用哪一个啊?一定要把它用对了啊,一定要把它用对了,那么这里它是一个关于 y 的运二次方程,所以说我们应该用的是 第二个,第二个,对吧?那用第二个,我们把这个具体的式子带进去,应该等于根号下 k 分之一的平方,也就是 k 分分之一,对吧?那要带 k 分分之一,我们首先要把这个斜率 k 把它算出来啊,已知这条直线,我们要求它的斜率, 他的旋律怎么求呢?有两种方法,一种是看到这样的一条直线,他是一般是,对吧? a, x 加 b, y 加 c, 等于零的形式,对吧?那么根据公式,它的斜率其实就等于负的 b 分之 a, 对吧?在这里也就等于负的负二, 负二分之一等于二分之一,对吧?可以这样来求他的斜率。那还可以怎么来求他的斜率呢?我们可以把这个 这个直线的方程变一下形变成什么呢?我们把这个二 y 移到一边去,然后再除以一个二,对吧? y 就等于二分之一, x 加上二分之一,那么就可以得到它的斜率,其实就等于 二分之一,对吧? x 前面的数其实就是二分之一,对吧?也就是斜率。所以说这两种方法都可以求斜率啊。如果是遇到这样形式的一个直线,那么它的斜率就是这个, 对吧?就是 x 前面的数,如果遇到这样形式的一个直线呢?它的斜率其实就等于负的 b 分之 a, 对吧?这个公式你可以直接把它记住,也非常简单,也非常简单。那么我们现在就来啊,写它的一个写成公式,我们把这里都擦了,都擦了, 那么它的一个形成公式就是等于根号下 k 方分之一加一,对吧?那么 k 刚刚我们已经算出来了,是等于二分之一的,那么二分之一的平方分之一,也就是 四分之一分之一,也就是四,对吧?四再加上一个一,那就是根号五,对吧?根号五,那再乘以一个 y 一加 y 二的平方,也就是四 p 的平方,也就是十六 p 的平方,对吧? 然后再减去四倍的 y 一百二,也就是八 p, 对吧?另,这个是指等于四倍根号下十五,然后呢,两边同时平方,你可以得到一个关于 p 的 一元二次方程,对吧?从而解除。 p 是等于二的啊, p 是等于二的,那么这个这个具体怎么算?你自己下去算了啊。很简单,只需要把它两边同时平方,然后得到一个关于 p 的一元二次方程,然后分解因式,就可以把这个 p 的值 求出来啊。那么有一个值要舍去,因为 p 是大于零的嘛,对吧?所以说这个就是第一问。求出来 p 是等于二,那么对应的它的抛物线的方程其实就是 y 方等于 c x, 对吧?那么这个就是第一问。
83数学熊🐻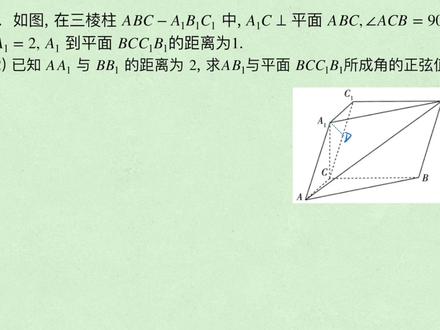 07:13查看AI文稿AI文稿
07:13查看AI文稿AI文稿十八题第二问又给了一个条件, aae 与 bbe 这两条棱之间的距离为二,求的是直线 abe 与平面 bccebe 所乘角的正弦值。这是一个线面角的问题,那么常规的一个做法呢,就是建立空间直角坐标系, 利用空间向量来求所乘角的正弦值。根据我们第一问的分析,在这个几何题当中, c a、 c b 和 c a、 e 这三条直线两两互相垂直,那么我们就可以以点 c 为坐标原点, 分别以他们三个所在的直线为 x、 y、 z 轴,建立这样的一个空间直角坐标系。而需要的点的坐标呢,就是所涉及到的这些点,我们需要 求出向量 abe 以及平面 bccebe 的法向量。这个平面的法向量,根据第一问的证明呢,它其实就是向量 dae, 因为这个线垂直于后面呢,这个平面点 d 是 c、 c、 e 的终点,所以向量 d a、 e 可以看成是向量 d c 加上向量 c a、 e, 那我们就需要知道点 a、 e 的坐标, 并且呢,向量 d, c 是向量 a、 e, a 的一半,因为它们两个平行,并且长度有两倍的关系, 所以再求出点 a 的坐标就可以解决这个法项量。根据第一问, a、 e、 d 是垂直于 c、 c、 e 的,并且 d 是 c、 c、 e 的中 终点,这个直角三角形中,斜边上的中线等于斜边的一半,而斜边的长度为二。直角三角形的两条直角边 aec 和 aece 就应该都等于根号二, 所以 c a 也等于根号二,这样点 a 一和点 a 的坐标都可以得到,那么向量 a、 b 一呢?这个向量我们可以看成是 在平行四边形 a b b 一 a 一中两条零边向量 a b 和向量 a a 一,他们两个的和, 所以我们还需要点 b 的坐标,那就需要求出 bc 的长度,这个时候我们看第二位所给的这个条件, aae 与 bbe 他们两个之间的距离相当, 两平行线之间的距离,我们可以过点 a 一找到 b b 一的垂线,那么这个垂线段的长度其实就是这两条平行线间的距离, 但是这个垂足会落在什么位置呢?那需要找到这个平行四边形边之间的关系, 我们可以连接对角线 aeb, 根据第一问, aec 是垂直于 cb 的, aeb 就是这个直角三角形的斜边,而 aebe 呢,是另外一个直角三角形 acebe 的斜边, a e c 等于 a e c e b c 又等于 b e c e, 也就是说这两个直角三角形对应的直角边都相等,所以斜边这两条 也会相等,那么这就是一个等腰三角形,所以这个垂线它的垂足就应该是 b b 一的终点。那我们继续写在第一问的前提下所知道的这个结论, a e c 等于 a e c e bc 等于 bece, 并且 aec 垂直于 bcaece 垂直于 bece, 所以 a e b 等于 a e b e, 那么我们取 b b e 的终点 e, 并且连接 a e e 可以得到 a e e 就垂直于 b b e, 所以它就等于这个条件当中所给的二。 那么接下来就可以放在这个直角三角形当中,求出 a e b e 的长度,它就应该等于根号下 a e e 的平方,加上 e b e 的平方, a e 是等于二的,而 e b 一呢,它等于侧棱长 b b e 的一半,也就是一,所以 a、 e、 b 一就是根号五,那么它的长度其实就等于 a、 b 的长度。这样的话,在直角三角形 a、 c、 b 当中, a、 c 是根号二, a、 b 是根号五, c、 b 呢,就应该等于根号三,这样求出他的长度来。以后,我们就可以写我们所需要的点的坐标,点 a 的坐标是根二豆零豆零点 a 一的坐标等于零豆零豆根号二, 点 b 的坐标零豆根三豆零。所以向量 ab 一就等于向量 ab, 加上向量 aae 等于负根二豆根号三,豆零, 加上负根二豆零豆根号二,最后就等于负二倍。根号二,根号三,根号二。 然后平面 bccebe 的一个法,向量 dae 就等于向量 dc, 加上向量 cae, 也就是二分之一倍的向量 aea 加上向量 cae, 那么就是二分之一倍的根二豆零豆。负。根号二加零豆零豆根号二,算出来这个 坐标就是二分之。根号二,豆零豆二分之根号二。根据线面所乘角的正弦值的求法,我们可以先设这个直线 a、 b 一 与那个平面所乘的角为 c 塔,那么三 c 塔等于 q 三方向。向量 a、 b 一 于发向量 d、 a、 e 所成,叫余弦值的绝对值,注意这个绝对值不要漏掉,于是就等于上面是点乘的绝对值。向量 a、 b 一,点乘向量 d、 a、 e 的绝对值, 下面是模成向量 a、 b 一的模,乘以向量 d、 a 一的模,那么上面是这两个向量点乘横乘横加纵乘纵加 数乘数,那应该等于负二加一,打了绝对值以后就等于一,而下面呢,向量 a、 b 一的模,根据根号下 a 方加 b 方加 c 方求出来,他应该等于根号十三。 同样的道理,利用这个坐标求向量 d、 a、 e 的膜就等于一,所以就是根号十三分之一。有理化以后是十三分之,根号十三,于是所求的这个角,他的正前值就是十三分之,根号十三。
212袁来有数(高中数学) 21:47查看AI文稿AI文稿
21:47查看AI文稿AI文稿今天呢,我给同学们在解析到二零二三全国假卷数学理科二十一题啊,这道题的提议是,已知函数 fx 等于 ax 减去口算一立方 x, 分子是 c x x 的范围呢,介于零二分之派一 a 的八十讨论 f 五 x 的单调性。 呃,第一问,呃,不给同学们详细说了,因为 a 等于八呀,把八带入,然后对 fx, 你就进行求导。求导之后呢?整理,整理以后呢?然后是 把分子分解音式,分解音式之后,我们就可以得到这个函数 fx 单调增减区间。呃, 这里计算量呢,稍微大一些啊。呃,他的答案是,零到四分之派,这个区间是单调递分。四分之派到二分之派,这个区间是单调递减。 我重点呢,说一下这个第二问。这个第二问呢,我们先采用的办法呢,是先拆后正。第四步, 他说若 f x 小于 c r x 横成率,求 a 的取值范围。 那么这个意思呢,就是说, a x 减去 c x 比上 q c x 的立方小 与赛音。二 x 横成立, x 呢,在这个范围内。 那么当这个式子横成立的时候,求 a 的取值范围是什么? 那么这个题呢,我们可以采用分离常数的办法,把 x 除过来,把这项移到右边。 但是如果分离长数的话,那么不是不能分离,是能够分离。但是分离以后构造的这个函数啊,这个求他的最小值,难度很大, 球倒以后啊,这个积产量太大啊,但是可以做,同学们也可以试一试。 呃,我们呢,还采用啥办法呢?采用啊,先拆后正。我们知道,当 x 取零的时候,这个式子写上内零啊,我们构造一个函数啊,我们构造零, 令 j x 等于 c n 二 x 加 c n x 比上 q c n x 的立方,然后再减去 a x, 我们只要证明他大于零横乘力就可以了,对吧? 他八二零恒成立,那么这个问题就解决,那么我们如何拆除这个 a 是什么呢?因为当 x 取零的时候,这个 j x 为零,根据端点效应,我们可以猜想, 那么既然是存在着这样的 a 使他的大于零恒成力,那么也就是说这个函数在零到某一个区间段内,那么这个函数应该是单调递增, 也就是说呢,他的导函数应该是大于或等于零成立, 然后呢,我们就可以通过他的导函数,然后把 x 等于零带入导函数去,让他大于或等于零,我们就可以得出 a 的一个取得范围, 然后呢,我们就猜想,这个 a 的取决范围有可能就是答案。 呃,这是一种方法啊,那么我还可以怎么去猜想呢?我们还可以这样去猜想,比如说我们可以先用竖行的思想,我们可以猜出 a 的答案,然后呢我们再进行证明。 你比如说这个,我们把 a x 移到右边,我们就得到。 那么如果把左边看成一个函数,右边再看成一个函数,这两个函数呢,都经过坐标原点, 那么我们可以进行这样的猜想, 那么根据他大于他合成率,我们就可以得得出这样的猜想,比如说这是左边的函数图像啊,这是零到二分之派, 然后呢,这个是经过原点的一条直线,如果让左边这个函数横在右边这个函数图向上的话,那么这个 就应该是这样, 根据图像看,只有在这种情况之下啊,他有可能是成立,也就是说我只要把左边这个函数在零零处的 切线的斜率算出来,然后呢,我让 a 比这个切线的斜率小或者是等,那么这个式子就应该成立,能看出来吧? 所以说呢,我们可以啊,先对这个函数进行求导,求出他在零零处的 切线的斜率,然后呢让这个 a 比切线斜率小或者是等,那么他都 成立,因为这个零啊,原点呢,是是不包括 x, 不包括原点,所以说呢,就是 a 等于这个切线斜对的时候,他也应该是成立的, 所以说呢,我们就做出这样的猜想,那么这个时候呢,我们可以对这个函数进行求导啊,对这个函数可以进行求导,我们就可以得到这个猜想, 或者是呢,我们就直接对着函数求导也可以了啊,那么这个的导数呢,实际上就是他的导数,对吧?所以说呢,我们就不另外再另函数了,我们直接就对这个函数进行求导, 求导是二倍的 q c 二 x, 然后再加上 分模式, 加上 在秤上,呃, c x 方应该是, 然后再减去 a 啊,这就是他的档,对吧? 呃,然后呢把口才 x 方约掉一个 对解。实际上你看啊,这个柿子啊,就是这个柿子,这个柿子我们可以再进一步整理一下啊,我们可以再整理一下,整理的结果是这个啊, 整理的结果应该是等于二倍的 投在二 x, 然后再加上 把这个三 s 方呢,变成一减去口袋 x 方,那么他就应该等于是三减去二倍的 再减肥。那么想一想,实际上你看啊,这个这个柿子 这个式的实际上不就是它的导函数吗?这对吧,就是它,它的导函数,那么它的导函数啊,在零零处的切线斜率时,把 x 等于零带进去之后,您发现这个正好是等于三, 这地方正好等于三,那么也就是说呢,此时啊,这个切线的斜率呢,应该是三, 所以说呢,我们猜想啊,这个当 a 小于或者是等于三的时候,那么这个式子就应该横成立。如果这道题要是填空题的话,那么这个题就完事了,你就知, 直接填 a 小等于三,应该就没啥问题,但这是一个证明问题,那么数形结合呢,不能代替证明。因此呢,我们还得需要证明,当 a 小于等于三时,他横成立。 同时呢,我们还得要说明,当 a 大于三十,他不横成立。那么如何说明他不横成立呢?那就是说,至少在零二分之配的区间上找到这样一个 x, 使得他不成立,也就是说使得他小于或在这才行。 那么通过刚才的分析看呢,我们已经猜想出啊,这个 a 应该是小于等于三,那么下面呢,我们就应该证明,当 a 小于等于三时,他大于零,合成率啊,再证明 a 大于 三十,它不横成立。好,我们现在看当 a 啊,这个可以呢,作为啥呢?作为啊,这个解析过程当中,在草纸上进行考虑,那么在写解析过程的时候呢,我们就可以把这些个过程呢忽略不计啊,也可以不考虑,对吧? 那么下面我看,当 a 小于等于三十,现在我们想证明他大于零恒成率,对吧?那么根据刚才呢,我们已经求助他的导数了,这个导数啊,我们知道 我们都可以呢,把这个 cosine x 方看成一个 t, 我们换圆一下,让问题变得简单一些啊,我们列 t 等于抠塞音 x 方,那么这个 t 的范围呢,那就自然在零和一 开局键内,对吧?那么这个时候,那么这个导函数啊,此时就变成什么了呢?变成二倍的,注意这里是二倍角余钱,应该是二七减一,对吧,再加上 底是梯方,上面是三减二梯再减去 a, 然后呢,我们再把它整理一下啊,再整理一下, 整理一下以后啊,就变成了四梯减二,加上 t 方分之三,再减去 t 方分之二,再减去 a 到这, 那么这个导函数啊,我要想说明它大于零行程率,根据端点效应, x 取零的时候, 他至少等于零,因此我要想说明他大龄同城力在这个区间上,我只要说明这个函数在这个区间上 单调递增就可以了,为此呢,我们需要说明他的导函数,也就是这个式子大于零横成立就可以了。 那么我们如何说明他大龄恒成力呢?这里是个问题,是吧,我们再令,我们再令啊,令 ht 等于等于这个数啊,等于这个 就是等于他了啊,等于他了。那么这个是 x 啊,等于是什么呢?等于这个四 t 减二,加上 t 方分之三,减去 t 分之二,再减去 a, 然后我们求下他的倒数, 他的倒数啊,我们求完以后不难得到啊,这样一个式,踢的立方 分子是四梯,立方再减去六,加二梯再减去六,是这样一个式, 这个七的范围呢,是零和一之间,那么我们看我们如何说明他正负呢?这里呀,分子出现了三次式,在这里呀,有的同学可能要有点困难, 这里头我们注意把它音式分解,或者是我们把它变一下的形,你看四加二正好等于六,所以说呢,我们 t 的一的时候,这个是正好等于零,因此呢,我们按照它有 t 点一这个音式进行整理,你看四七立方, 你给他减一个四 t, 然后加个四 t, 再加个二 t, 六 t 正好减六,等于 t 的立方提出是七,然后是七方减一,再加上六倍的七减一, 那么由于其小于大人啊,那么这个狮子显然是一个副的,对吧?我们就不用再进行分解了,肯定是副的,因此 这个函数啊, h t 呢,应该是单调递减,对吧?所以 h t 应该 是单调递减,对吧?那这样一来的话呢, h t 那就应该大于 h e, 而 h e 的概率之后呢,正好等于三减 a 等于三减 a, 而 a 小于内个三,说三减 a 呢,显然是大于等于零,因此啊, h t 我们就证明出了他大于等于零,这个 h 七是谁呢?就是这个导函数啊,他大于等于零,他大于零,对吧?导函数大于零,所以说呢,我们就得了函的得到啊,这个导函数是大于零, 那么导函数大于零呢,我们就得到了 j x 大于 这一节,对吧?那么这一节,正好这一节,也就是说呢,我们证明了,当 a 小于这个三十,他大于零,是恒成立啊,这没有问题啊, 那么下面呢,我们还得看一下啥呢,当 a 如果要是大于三的时候,他不合成率,这个还得需要进行说明, 那么当也大于三十,他为什么就不恒成立了呢?这里头呢,我们要找到一个返利就可以了。 我们首先呢,我们看一下啊,这个函数是递增的还是递点的?我们先看啥呢?我们先看这个导函数啊,这个导函是不是递增的还是递点的?你看看能不能看出来,这个导函数十 实际上就是由 t 等于抠塞音 x 方,对吧?和 h t 啊,就这个实际上就是 h t 啊, 他俩复合而成的,对吧?是不是复合而成,由他,他俩复合而成就是这个倒霉数, 那么这个函数显然在零一这个区上单调递减,这个呢已经证明出来了,他呢也是单调递减,两个都是单调递减,所以说呢,复合以后的这个函数呢,他就应该是单调递增, 也就是说啊,这个函数的导函数是个战斗递增说,对吧?那么下面呢,在这个基础 之上,我们来说明,当 a 大于三的时候,他为什么不合成?我们要说明,当 a 大于三时, 他不合成立,当也大于三十啊。我们刚才啊,已经说明了,这个 j x 的导函数,他是单到第三位,对吧?因为 j x 在零到二分之派这个区间上,它是单调递增,并且呢, 我把零带入,我们得到是什么呢?是三减 a, 对吧?是 是二三减 a, 因为 a 大于三,所以说呢,他应该是小于零啊,那么也就是说什么呢?这个 j s 图像啊,他应该是这样, 但是这里有一个问题,那就是当 x 取何值的时候,这个 js 导函数啊,应该取正的呢。哎呀,这个点呢,很难取啊,很难取啊,这个我暂时还没有想 到,但是呢,我们可以通过极限的思想,当 x 趋向于二分之派的时候,我们考察一下这个导函数,他的极限是什么呢? 也就是这个式子啊,指导 f 这个式子,当 x 趋向于二分之派的时候,它趋向于负,二分子呢,是趋向于三, 而分母呢,趋向于零,整个的式子呢,就趋向于正无穷,所以说呢,减去一个长数,也趋向于正无穷。 所以说呀,一定存在啊, x 零属于零到二分之派 这个范围内啊,这个就是 x 零,对吧?实则呢,这个导函数在这个区间上 为负,所以说 j x 在这个区间上,那就是单调递减,所以我们就有 j x 零小于 j 零,而 j 零正好等于零。这就说明啊,当 a 大于三的时候啊,他大于零不合成立,我们找到了一个 s 零,他小于零。 所以说呢,综上所述,我们就得到了这个 a 的取值范围呢,就是小于等于三。
163伯麟数学 15:00查看AI文稿AI文稿
15:00查看AI文稿AI文稿好,我们一起来看一下第二十题。射抛线, cy 的平方等于二 pxp 大于零的焦点为 f, 且点低的坐标为批斗零过 f 的直线交西于 m n 两个点。当直线 m d 垂直 x 轴时候, mf 等于等于三,要求 c 的方程。我们把图做一下,顺便把题目的条件给翻了一下, 开口朝右的抛线, f 为焦点,而且呢,第一点为 p 到零, 此时呢, m d 垂直走,那 m 脸在这里,这是垂直的。好,我们说,呃,我们说了,有抛线的话,就一定要把它的准线也带出来啊,我们说准线,你教你,我们标的有一个 fvp。 好,那此时呢,他告诉我们的条件, mf 等于三,这条是三,那我们知道呢,抛线上的点到焦点的距离和他的准线的距离永远相等,即这条,这是 mp, 垂足为 mp, 即我们的 mm 一撇是等于 mf 等于三的,对吧?我们的,我们又知道了,这是一个是垂直啊,也就是说 md 是垂直于 x 轴的。那所以我们的 dm m e p f e p, 它会构成一个举行,那此时 m m m e p 会等于我们的 f e p d, 我们标注原点,那此时 m e p d 又等于 f e p o, 再加上我们的 o d, 对吧? f e p o, 我们说是准线到准线到这个距离,这个距离应该是二分之一 p, 那就是二分之一 p, 再加上 odod, 第一点就行,坐标已经给了,他的坐标就是 p 到零,那所以说 od 就是二, lot 直接就是 p, 他等于多少啊?等于三,这个好,我们解救方程来解一下,应该得到屁就等于二。 好,那所以呢,我们的 c 的方程就为 y 的平方等于四 x。 好,第一文搞定。好,我们接着看第二文啊。设直线 md 与 nd 与 c 的另一个交点分别为 ab, 然后呢, gmnab 的倾斜角分别为阿法和贝塔,要求当阿法减贝塔取得最大值时,求直线 ab 的方程啊,那此时 md 呢? 未必在垂直的走,对吧?那我们要重新做一个图来分析一下, 这是 f 点,这是 n 点,这是我们的 m 点,那第一点在这里,那此时我们看啊,那此时 md 与 x 与抛出另一个焦点为 a, 这边呢,是 n, d 与抛线的另一个焦点,为什么为 b? 这点为 b? 要求 ab 的 ab 的方程,而且呢,这个几级角阿法,这个几级角贝塔,而且阿法减贝塔取的最大值是 ab 的方程。 好,那我们看啊,那我们明显的我们知道的是什么?开 mn 它是等于什么?它是等于填紧阿法的 k 呢? ab 它是等于什么?填紧贝塔,对吧?当然阿法和贝塔不等于九十度的情况下才有。这样啊,也是说 mn 九邪率, ab 有邪率情况下才是这样子的。 你的情况啊,那如果是什么,那其实他要求的是阿法减贝塔的最值,那我们就很容易想到什么,那要求天晴的两角的差才能把这两个条件给用上去,那就天晴的阿法减去天的贝塔,它就等于什么?天晴阿法减去天晴 a 塔除以两个香肠,一加上两个香肠,那么就是如果有斜溜就可以把房里带了,对吧?那直接就是 kmn 减去 kab 除以一减一加上 kmn 乘上 k, a, b, a, b 这个字。好,那前提是这个有斜率的情况下啊,那如果没有斜率呢?没有斜率,我们单独讨论一下吧。那此时什么?只要我们的什么?我们知道天晴只是个单调的函数,但是递增的一个函数,对吧?当然在一定的区间内啊, 当然例中的函数。那此时我们天津阿法减贝塔,如果他取得最大,那是不是阿法减贝塔有可能取得最大值呢? 那本题我们就不将天津呃阿法和贝塔的最大值转成了天津的最大值。天津阿法减贝塔的最大值,即求这个市值的最值, 整个这个是最值。好,那我们就单独分析一下如果他无学历的情形,如果无学历的话,也就是说,那此时我们的 mn 呢?他是垂直的, 这是我们的 m, 这是我们的 n, 这是 d 点,那我们做一个,这个是 a 点,这个是 b 点。好,我们有对唱性可知,那此时这里是垂直,这边也得吹什么垂直,因为什么?图像是关了 x 对唱的对吧? 好,那此时如果阿法等于什么?九十度,那此时贝塔也得等于多少?九十度,那此时阿法减贝塔应该等于零了。 好,那我们再看看无旋律的情形啊。无旋律的情形,那我们是要想办。呃,有旋律的情形,然后有旋律的情形呢?我们也想办法把这个 kmnkab 给表示出来, 摇出来,才能够求出整个这个天津阿法,也就是这个式子的锥子。好,那我们把过程好好书写一下,我们把它擦掉啊。 嗯,把这个分析过程我们先擦掉了啊, 第一位也擦掉了,第一位的过程我们也擦掉了。戴板带书写的攻击不够啊。 嗯,好, 好,我们来详细写的是书写过程啊,要问的书写过程好, mn 无邪律, 这是阿法,等于九十度,由对由对称性合织, 我们直接写就可以了啊,因为前面分析过, 呃,这是杯塔,也等于什么九十度,那这是阿法减杯塔就应该等于零。好,第二种,若什么?若 mn 有邪率, 那此时我们把它旋律设为什么有旋律设为什么设为 k? 这位可以,那此时我们知道 f 点的坐标应该是一到零,因为前面我们得到它的方程是 y 等于四, y 方等于四 x 这个,那 f 应该是四到零。好,那我们就可以把 m n 的直线射出来了。 m 的直线方程, m 的方程就应该为过一个定点啊, y 减去 y 零, y 零是零, y 减零等于 k 乘上 x 减去 f 选的注行坐标一的这个直线。 好,然后呢,我们接下来还得把什么?还得把这四个点 mnab 是不是得射出来啊?把 mnab 射出来。好,那此时我们射什么?那怎么射这个比较好,比较好呢?如果啊,我们写上面如果我们把 m 点的坐标啊,假设我这样 m 点的坐标设为 x 一, 那我是不是要这个点 m 点是在抛线上头的,那是,我是想办法把这个 y 给求出来,那只是 y 方就等于什么 wifi 等于四倍的 x 一,那我要解这个 wifi 的时候,那 y 我就开方了啊,开方是出现正负 四 x 一。哎呀,那麻烦大了,如果我射 x 不太好办,对吧?如果把它杭州标用 x 表示,那重坐标就不太好表示了。这有个正负,这里有点麻烦,那我们最好怎么射呢?我们射 y 吧。这样啊, 也就是说我们的 m 点的坐标,我们不可以把它设套为 y e, 它为 y e 的话,那此时 x 是不是很容易表示了? x 就等于什么?它是食堂坐标,那就 y e 的平方等于 四倍的 x 一,那 x 一就等于什么?呃,四分之 y 一方,好,那所以说它得了它的横度标就应该是四分之 y 一的平方。好,同理,我们一样可以把 n 点的坐标弄出来啊。 n 的坐标,那应该就是 y 二吧,那这个上前头就是四分之 y 二的平方 好,再把 a 点 a 点设为 x 三吧,那就是 y 三了,不是 x 三啊, y 三,那同理,它就是四分之 y 三的平方, b 点呢?为 y 四,这个点为四分之 y 四的平方。好, 那我们是不是得连力了,想办法是吗?连力了啊,那就连力哪个呢?直线 y 等于 kx 减一, 然后呢? y 的平方等于四 x, 好,此时我们削什么?因为我们这些点做标,刚才说了是用什么?用 y 表示更方便,用 y 表示。那所以说我们这里可以肯定要削 x, 留 y 留 y 啊,那就是削去。 想要去 y h x, 得来这个自己整理啊,我们整理一下就得到。什么?四 k 分之四, k 分之什么? y 发,再减去 y。 哎,我没有发啊,减去 y 再减 k 等于零。 好,那么回答,那就是 y 一加 y 二,管他有没有用啊,先写出来,先 yy 二等于负的 a 分之 b, 那就等于 k 分之四,好,那 y a 乘 y 二等于什么? a 分之 cm, c 等于负四。哎,这是个刚好这个长数了。好,那我们此时接着往后啊,那此时我们的我们是不是还得把 md 给弄出来? md 的弄出来才能确定 a 点的坐标啊,是吧?这个 m 点和地点去确定了一个 a 点,那是把 md 的方程弄出来,那在 m 点坐标,我们一射出来这里,那地点坐标呢?地点坐标是 p 豆零也是地点坐标是 我们补到这里啊,地点坐标应该是二到零。好,那么两点四直接直接得到 md 的方程啊,两点四吧,那就是 y 减 y 减第一坐标,第一点中坐标,然后呢,横坐标 x 减去第一点的横坐标,直接等于 y 一减零 这两个,这两个点 y 减 y 这边,那就是四分之 y 一方减去二的,这个好,带入哪里?带入 c 消去什么一样消去 x 好整理得 啊,这个整理我们就去整理啊,整理出来了肯定就上九八五了,整理不出来的也能上二幺幺啊。那我看啊,整理应该得这个二 y 一,然后呢,二 y 一的方减八,再乘上 y 再减八,等于零。 好,一样回答,这是回答 y, 注意啊,这是回答,这个点是 y, 这个点是这个点是 y e, 这个点是 c 点。什么?他的焦点是 m 和 m 和 a 啊,那所以说此时他的回答应该是 y 一加 y 三这两个点,它的焦点是这两个点啊,这两个点 y 加 y 三,那就等于 负的 a 分之 b, 那就是什么?我们整理玩具的二 y 一方减八,上头是二 y 一好, y 一乘 y 三就等于负八。哎,那这里有关系哎, 对吧?这两个有关系啊,那所以我们把它比掉吗?得到 y 二和 y 三这个关系,是不是?那也是说 y 三就立马就等于二倍的 y 什么 y 二了,哎,所以有这个好,发现一个东西,发现一个好东西 好,那我们接下来还得把 n d 啊,同样 n d 用两点四,把 n d 的方程也表示出来, y 减去地点的重坐标零啊,好, x 减去地点的行坐标二等 等于什么?等于我们的恩典的恩典是恩典的重坐标 y 二减去地点的重坐标。比上什么 dn 点的横坐标四分之 y 二方减去 d 点的横坐标二好,那 nd 的方程出来了,一样带入, 那就是消去,一样消去 x 啊,好,消去 x, 那我们什么?那我们就会整理出 y 的平方等于二, y 二分之二, y 二方减八, 再乘个 y 减去八等于零,我们减这个整理的这个好,再回答了 y, 那此时注意啊,此时 y 一 y 二嘛,不要太随意啊。那此时 点的坐标是什么?是 y 二,然后呢? b 点的坐标是 y 四,那所有此时应该有 y, 它的两个根应该是 y 二,加上 y 四等于负的 a 分之 b, 那我们单元区应该得到二 y 二的平方减八分之二, y 二,好。还有一个 y 二乘 y 四 好, y 乘 y 四,他得到了负八好,那此时一样会得到什么? y 四等于什么?这个跟哪个呢?跟第一,跟第一个,这个是指, 这个是我们可以一比一下,马上把消,把 y 二给消掉了,那此时会得到 y, 所以我们的 y 四就等于二倍的 y 二好,那此时我们要把什么?要把 k, 要把这个 k 给表示出来一下了,这个 k, 它直接就等于什么? kab 表示一下吧, kab 就等于 好, kab 呢?那就等于什么? a 点的横坐标相减, a 点的什么?重坐标相减,这个 y 三减 y 四 减去 y 四,再比上横坐标相减,横坐标相减呢?那应该是四分之 y 三方减去四分之 y 四方。 好,把这个表示让我们看看。那此时他应该我们整理一下,下头可以用平方插功式,对吧?变成 y 三减 y 四。括号乘上什么括号? yy 三加 y 四。好,那我们一整理完,刚好就得到四分之 y 三加上 y 四。
78莫默有文 11:40查看AI文稿AI文稿
11:40查看AI文稿AI文稿ok 哈,各位同学大家好。呃,我这边是已经拿到这个二三年全国假卷的这个题目了,然后整个浏览了一下,发现整套卷子的难度相比于去年是要 呃低很多的,而且啊,让我不是很理解的地方是今年这个平抛这个点竟然出现了三次啊,这是有一点不是很好理解的一件事情啊。这个我觉得出题可能还是有一点 呃有一点点小小的问题哈。啊,然后那我们今天就来聊一聊这个假卷的这一道压轴题,现在高二的同学可以自己尝试来做一做,自己点一个暂停。好吧, okay, 那我们一起来分析一下那这道题呢?呃,主要其实现在比较适合高二的同学来听,因为高一的同学还没有接触 触到这个电磁感应的部分啊,也可以听个热闹好不好?好,我们一起来看一看。那这道题告诉我们的条件有哪些呢?第一个是光滑对吧,我们不用考虑摩擦了,然后紧接着告诉了我们间距为 l, 两根杆的长度也都分别恰好为 l 对吧,都没有超出。 ok, 那么这个我们知道了之后呢,我们知道其中一根杆的质量 vm, 并且它是带电阻的,而另一根杆非常有意思哈,质量为三 m, 但是它是一个什么 绝缘棒,所以我们要知道在这个地方是一个双干问题吗?你应该可以判断出来了,不是一个双干问题,是一个伪双干问题对不对啊?这个 q 这根绝缘棒因为他是绝缘的,所以并不会有电流通过,也就意味着他并不会受到安排力的作用对吧?真正要考虑到的这个 其实只有 p 了,对吧?啊?真正要考虑到受安培力作用的其实只有 p, ok, 好,这个不再多说。那么接下来以大小为为零的速度,他会与这个 p 发生一次碰撞,而且整个碰撞是一个弹性碰撞,碰撞时间极短啊,这个不用去考虑。那么最终呢?从右侧滑出,并且 啊落在了地面上的同一点,好,我们知道一旦他从右侧滑出了之后,这些都开始做一个什么样的运动了,做一个平抛了,对不对?对吧?做平抛之后,他们能落在地面上同一点,又从同样的高度抛出,要落于同一点,那一定 马上反应过来,这告诉了我一件事情,就是什么啊?这个,这两根杆有相同的抛出速度,对吧?有一个相同的抛出速度啊,有一个相等的这个抛出速, 速度 v 零一飘板,因为 v 零用过了,对不对?啊?啊,有一个相同的抛出速度,好,那接下来再来 p 在导轨上运动的过程当中,两端啊始终是接触好的,这些都没什么好说了,对吧?首先我们来看第一个,问,金属棒 p 划出导轨时,他的一个速度应该为多少, 对吧?那这件事情怎么来呢?啊?我们乍一看,好像这个这个还不是那么好聊,那么一步一步来聊,首先发生的第一件事应该是这个弹性碰撞,因为有弹性碰撞这个信息在,所以马上列出两个式子来,第一个应该是 m v 零,对吧?动量守恒, m v 零对应的应该是一个 m 乘以之后它的速度,这根杆叫做 p, 对不对?所以 m v p 加上一个什么呢?加上一个这个三倍的 m, 是不是另一根杆啊?再来乘一个 v q 啊?那这, 这是一个动量守恒的关系,再来一个动能守恒,对不对?弹性碰撞二分之一 m v 零方,对应的是一个什么呢?二分之一 m v p 的平方,同时再来加上一个二分之一三 v q 的平方, ok, 好,所以这是我们得到的这个根据弹性碰撞能得到的相关信息,然后紧接着根据他,我是不是直接可以解出来了,解出来之后呢?这个 v p 应该是多少呢?应该是一个这个二分之一倍的啊 v 零 对吧?好,解出来应该是一个二分之三,对吧?这,这应该是一个二分之三倍的 v 零,同时呢,我这这个 v q 也可以求出来应该是多少?应该是一个二分之一倍的 v 零,好,这是我们根据题干可以直接解出来的,但是 他要问的并不是这个,他要问滑出时候的速度,我们知道将来 p 要干嘛呀? p 要干嘛?在接下来过程当中,是不是因为你运动,对吧?你有速度微了啊,所以你会切割磁感线,从而产生电动式,整个回路当中就有感应电流了,就会干嘛让 p 减速,所以接下来 p 是要减速的呦, 对不对?那么他最终飞离的速度应该怎么来算呢?这是不是小卡了一下?但是你千万要记得刚刚有一个非常重要的特殊关系是什么? 是不是他们落于了地面上?同一个点,也就意味着抛出时二者的速度应该是相等的啊,所以也就意味着最终的这个 p 的飞离速度,对吧?最终的这个 p 的飞离速度 啊,这个最终的这个飞力速度 v p 啊一飘,其实应该是等于什么?等于 v q 的,因为 q 接下来是匀速运动,对不对? q 不会受到其他力的作用了,安倍力不瘦,又没有摩擦,它是匀速运动啊,所以最终呢,又要跟 q 速度相等,说白了就是你非离的时候啊,所对应的这个 v p 漂 其实就是什么?就是二分之一杯的杯龄啊!第一个问就结束了,对吧?那么接下来再来第二个问啊,金属棒劈在导轨域上,运动过程中所产生的一个热量为多少?那这个就很简单了,对吧?整个回路上所消耗的热量来自于哪呢? 安培力对这根杆做复工啊啊,所以这根杆的动能减少了,所以所消耗的全部的热量,其实无非就是一个二分之一 m 啊, vp 的平方,对不对啊?初动能乘一个 vp 方,减去它的末动能 a p 一飘的平方, ok? 好,所以于是这样简单操作一下,得到的这个结果会是多少?我们简单来算一下吧, 他的这个碰撞之后的这个出动呢?应该是一个多少呢? vp 应该是一个这个,这个四分之九,对不对啊?威凌风,然后再减一个,这是四分之一倍的威凌风,应该是四分之八,也是二倍,对吧?所以刚好和外边的这个二消掉,得到 mv 零风, ok 啊,所以于是得到的产生的热量应该是一个 m v 零方啊。第二个问非常简单啊,再来看第三个问, 第三个问要问到的点在哪?他说碰撞之后 q 在导轨上的运动什么时间? ok? 时间这件事情我们要怎么去找?哎,我们会发现 在这我唯一能够知道的信息似乎就只有 p 碰前的速度和碰后的速度,而我们在这又要考虑时间,那马上反应过来, 对吧?而这知道的是速度的改变关系,对吧?其实严格意义上来讲,你拿到这个问题,他直白说的是谁的运动是 q 的运动,所以你直接应该想到的是直接用 q 加了要跑的位移来除以 q 的速度,因为 q 是匀速运动,这很简单,可是 你发现找不到这个位移,所以我们不能从这个方向去想,那我们接下来怎么去想呢?接下来怎么去想呢?是不是唯一能跟时间扯上关系的?我们先来看第一个,他在强调时间,第二个 啊,我们知道的是速度的改变情况,对不对?至少我知道 p 在整个过程中速度的改变情况,于是你应该想到什么?冲量等于 动量的改变量,对不对?所以你一定只能往这想, ok, 因为如果我想要去聊这个这个做工的话,我的条件是不够的,因为我并不知道这个 x 对不对,所以我没办法找到。而且整个过程中安排力是一个便利啊,所以从功和能量的角度,这没办办法去解决。所以我们只能啊根据这个题干这个时间上的暗示,以及我们知道速度变化的一个这样的一个暗示,我们知道这应该要用冲量去解决 啊,所以于是将来应该是什么?冲量等于动量的改变量,对于我这个啊 p 来说,应该是发生了一个什么状态,应该是 m 乘以 v 零减去一个啊,这个这个这个这个,什么 v p 啊?呃,这应该是什么啊? v p 对吧?碰后我们只聊碰后的情况,对吧?啊? v p 减去一个 v p 飘,对不对?这应该是动量 的大小的改变量,对不对?所以等于冲量的大小啊,冲量的大小应该是什么呢?应该是此时由什么力来产生冲量?是不是有安排力?安排力怎么写?是不是 b i 啊,再来乘以 l, 再来乘以 t。 但你要注意一件事情,各位, i 在这是一个什么? 是一个变化的值,所以如果我们要用这个式子的话,我必须要去找的是 i 的平均值,所以这个式子怎样才能成立?你必须把 i 给我带成平均啊,在这是不是才能成立?好?那这件事情知道了之后呢?接下来我们又知道了一个什么关系呢? 啊,我们又知道的,其实 i 的这个平均值应该等于多少?是不是应该等于的是整个过程的 b l v 的平均值,对吧?啊? v 的平均值再去除以 什么呢?再来去除以这个回路的总电阻是不是仅有的这个 r ok 吗?好,那么这两个式子连力啊,我能不能够去啊?这个这个去进一步的去求解了呢?是不是可以了?为什么?因为我们接下来是不是就会发现,我得到关系应该是一个 m 乘以 vp 减去 v p 漂,其实得到的就应该是 b l v 的平均值,对吧?其实啊,这儿乘上去就应该是 b 方 l 方 啊,除牙下来是 v 的平均值乘以时间,那得到的是不就是干的水平位移?其实你这应该马上能背下来的哈,这其实对应的应该是什么?动量改变量?应该是 b l q, 对吧?应该是 b o q, 好,那么接下来这个 q 可以怎么来?表示?用 dirt five 除以整个回路总电阻 r, 对不对啊?所以, 所以如果你能反应过来这件事情的话,可以更快一些。 ok, 我们这相当于又给大家推了一遍,好,所以由此我是不是可以解出来了,对吧?啊,解出来了,这个 x 应该是一个什么样的值? 是不是这两个 vp 减 vp 漂的一个差值应该是多少?本来是二分之三线的是二分之一,是不是差值刚好就是一个 v 零,对吧?就是一个 mv 零啊,就是一个 m v 零,再来乘以一个 r 除以一个 b 方 l 方,而最终我们要解的这一个所谓的时间 t, 因为接下来的过程是不是做的是匀速运动,直接用 x 来除以 v q, 对吧? q 是匀速要跑完的,是相同的距离,对不对啊?所以除以这个 v q, 而这个 v q 是多少啊?就是二 二分之一倍的 v 零,对吧?就是一个二分之一倍的 v 零,所以除以个二分之一倍的 v 零,得到的结果应该是什么?二倍的 m r 除以一个 b 方 l 放,那么整个问题也就结束了,其实这就是假卷的压轴,整体来说难度还是相对来说比较简单的。 ok, 好,那么最后还是一样哈,老老规矩,对吧?啊, 大家这个后续还有其他什么想让我讲的这些具体问题啊,都可以在群里面问啊,那比较典型的我就会给他出成视频, ok 啊,后续会给大家有这个具体的这个答疑的这一些时间,好吧啊,我会考虑每周抽一次来给大家做一个直播啊,直播答疑。好吧,那其他的我们就不再多说了,以上就是我们今天给大家聊到的全部内容。好,各位拜拜。
 14:41查看AI文稿AI文稿
14:41查看AI文稿AI文稿大家好,今天我来讲一下二零二三年全国假卷的立体几何大题。通过这道大题的讲解,我其实想告诉大家一个道理啊,就是间隙法在立体几何大题中真的不是万能的,很多立体几何的大题,其实不能用间隙法或者用间隙法,它的计算量太大 来,真正聪明的同学啊,应该是立体几何,他的间隙的方法还有纯几何的方法都应该掌握,都应该灵活运用。我们看一下这道题,他说的是三棱柱中,这个三棱柱的话,他可不是直三棱柱,他这个侧棱是斜着的啊,这一看就能看出来, 然后呢,继续往后读,他说什么呢?他说的是 a a 一等于二,就是侧棱长啊, a a 一, b b 一, c c 一其实都等于二。他告诉你谁垂直于底面呢?他说的是 a、 e、 c 这样一个侧面的面对角线, 它是垂直于 a、 b、 c 这样一个底面的,它垂直啊,并且告诉你这个角,也就是说 a c 和 b c 夹角是九十度吧,也就是说什么呢? a e、 c a c、 b c 这三条线两两之间是互相垂直的,可能到这之后的话,很多人就直接 x 轴、 y 轴、 z 轴写上了。这第一问肯定不是这样来正的啊,根本就没有必要去间隙,不是用间隙法来做的。那么我们看一下 它最后还有一个条件, a 一到平面,它的距离是一。我呢,反正读完题之后,我就看到了一个一,一个二, 反正再加上两个垂直呗。好,一二垂直,那你能不能想到在直角三角形中,斜边中线等于斜边一半这样一个一比二的道理啊?肯定能吧,那么我们来看一下 这道题啊,第一问的话,真的特别简单,我们就找重点啊,斜边重点等于斜边一半,哪个平面呢?我们把这个侧面啊,也就是 a e a c c e 这样一个平面呢,他这个侧面画出来他的平面图,画完这个平面之后的话,首先垂直底面,不用多说了吧, 既然你这个 a e c 是垂直于整个底面 a b c 的,它肯定垂直于 a c 啊,那进而也垂直于 a e c e 啊,是不是?好了,肯定这个垂直是好得出来的,得完这个垂直之后的话,为什么要找终点呢?首先斜边中点的一些密码,这是二吧, 这是一吧,点 o 在哪啊?你要注意啊,在这样一个立体几何的原图中,这个点 o 它指的是 c c 一的终点,那么点 o 它记在 c c 一上面,那肯定就是在平面 b c c b 以上的。好了,不用多说了,看好了啊,因为什么我们分析一下这道题,很容易证明呢?这个 a e c 是垂直于 a e c e 的, 并且呢,再来看这个 a e o 斜边中线等于斜边一半吧,它就是斜边 c c e 的一半,等于一啊, 那么既然点 o, 他是在什么?他是在平面上的,我知道了,其实你看了啊,因为 a 一点到,请告诉我,在初中阶段学过这样一个定理,没有点到直线,除以现在最短吧,那高中的话,我们就知道了,点到什么? 点到平面,他其实也是垂线段最短的,最短最短,最,就是唯一的意思啊,就是那个垂足只有一个的意思, 其实那个点 o, 它就是点 a 一到平面,哪个平面我写清楚啊?到平面 b c c 一 b 一的这样一个垂组,那个点 o 就是垂组,懂了吧?它的距离 我写清楚了,距离为一,所以再加上什么,所以我就知道了呀,其实 aeo 它就是垂直于整个平面 b c c 一 b 一的,剩下不用多说了吧。然后呢,也很容易证明的一点是什么?也很容易证明的一点是,首先我们可以通过证明谁通过证明这个 b c 垂直于整个 侧面 a c c 一 a 一,然后进而证明两个平面,也就是说平面 a c c 一 a 一,它是垂直于我们的 目标平面 bccebe 的。为什么呢?原因很简单,首先我已经分析过了,两两之间互相垂直吧,既然他这样一个 bc 垂直于平面里头两条相交直线,所以就垂直于整个平面,进而呢,就得出来这样一个面面垂直了,那得出来面面垂直的话,你说这两个平面 它的胶线是谁啊?这肉眼可见的嘛。胶线,两个垂直,平面的胶线就是它垂直于胶线则垂直,平面,垂直于平面则垂直于它俩的胶线吧,这是一个定力点,所以其实 a u 它是垂直于整个 c c e 这样一个胶线的。 那既然证明完这一条的话,所以不用多说了吧。点 o 既是垂直的,它也是终点,所以 a u 是什么?是中垂线呀?中垂线它的性质定理是什么?中垂线上的点到 线段,两个端点距离相等,所以它这个 a e c 等于什么?就等于 a e c e 啊,那 a e c e 显然是等于 a c 的,不就证明完了,就这么简单, 懂了吧?点到平面垂线呢,最大它的距离就是一,这道题给的太明显了,一个二,一个一,加上两个垂直,肯定是要想直角三角形中斜边中线等于斜边一半这样一个定律的。我们继续来看第二问啊。第二问的话,如果你要选择用间隙的方法,不是说不能做,我说一下 间隙的方法有什么缺点啊?间隙的方法的话,咱们根据第一问这个图形的话,很容易判断这个 a e c 和 a c 它的距离的话,肯定是等于根号二的啊,这个都很容易算,也就是说 a 一点,还有 a 点我们坐标呢,都是可以写出来的, 然后包括这个 a 一点,我们可以写什么?那 z 轴当然是零,逗号零,根号二了,但是 你想写 b 点吧, b 点的坐标你得假设了,只能假设零多少 t 零,你还得把这个 t 求出来。根据线与线的这样一个距离, 是不是还得做辅助线,比如说 b 点啊,做了一个垂直,比如说垂直于他,然后 bh 的长度是等于二的,然后再进而用什么用 啊?要么是点臂到向量的距离公式,要么就是根据平面向量他这样一个投影的公式,当然 他这个空间下来也可以用投影公式啊。所以说这道题的话,剩下的计算量会很大,然后再把这个 t 具体的话是等于根号三算出来。这个咱不推荐这种方法,你看看如果这道题 用纯几何的方法,他有多简单啊。看了,首先这道题的话,有一点很明确,你看刚才我们在证明的时候,这个 aeo 是不是垂直于整个平面点好, 这道题的话,我连接一下 a b 一,为什么连接这个 a b 一呢?道理很简单,因为你求的就是 a b 一和整个目标平面的它夹角的正线值。这个平面的话不用多说了吧,我就擦掉了啊,平面是在这样一个位置的,在后边, 那么看线面角,它的平面角需要找出来。其实线面角它得有三个要素。首先第一个要素就是 就是斜足,斜足就指的是斜线 a b 一和平面的焦点,斜足当然是 b 点了,不用多说,斜点的话是我发明的这样一个名词,其实就是斜线上的异于斜足的一个点,那就写成 a 点, 没他有这样一个点过, a 点还得做出些什么,他其实缺少了。第三个要素,缺少了垂足,对吧?比如说我们做 am 是垂直于整个平面哦,所以当你想到这一点的时候,我觉得辅助线其实就很明确了。首先第一条辅助线我先告诉你啊,我们只需要做 am 怎么样? am 是平行于 d 问中的 aeo 的,他俩之间是平行的呀,再加上别的平行交臂啊。知道了,那有了这样一个平行之后的话,再加上这个 aae 是平行于 cce 的,肯定很容易出现一个平行字边形吧。咱们写上啊, 这个平行四边形呢,就是 a m o a e 能得出来,那根据平行四边形结论的话,是不是很容易就得出来 a m 的长度了呀?它和 a u 的长度其实都是等于一的, 对不对?那做完这个之后的话,效果是什么?你为什么要做这个 a m 平行于它呢?道理很简单,因为在第一文中我们已经说明了 a e o, 它就是 下面垂直的那样一条垂线,它是垂直于整个目标平面 b c c 一 b 一的。所以既然平行的话,你这个 a m 是不是也垂直于整个平面 b c c 一 b 一啊?它想告诉你的就是说 m 点, 他就是线面垂直的这样一个垂足呀。得出这个垂足来之后,你看线面角的三要素都有了啊, a m 是整个平面 b c c e b 一他的垂足吧,点臂是斜足,他是,哦,连接起来我知道了,如果我再说的明 这些,其实就是这么的回事,这是 a 点,这是 m 点,这是 b 一点,那这个 am 等于一。已经算出来了啊,它的长度等于一,那么其实我们只需要算一下 bm 或者说啊 ab 的长度就行了。 这道题我们选择算一下 b、 e、 m 的长度,是不是就把这个正弦值算出来了呀?因为这道题,他这个线面角的平面角其实就是垂啊,我写出来他这个线面角的平面角,其实就是让我们求哪个角,求这个角 a b e m 它的正弦值,显然它的正弦值 a b e m 是等于谁比上谁了,你就告诉我,其实就是等于刚才我画的那样一个直角三角形 a m b e 中的它这样一个 a m 的长度,再比上谁的长度,再比上 a、 b、 e 的长度, a b e 长度的话,我觉得不太好算啊, a b 是斜边,我们就用勾股定理来算吧, a m 显然等于一, 它下边这个斜边。关于这个 a b 一的话,我们就用这个 a m 的长度的平方,再加上 b e m 的平方。所以这道题其实我们只需要算,是到现在为止我分析清楚了,只需要算 b e m 的长度啊,你既然要算 b e m 的长度的话,是不是要涉及到勾股定理啊? b e m。 好,现在看了 b e m 可以放,把它放到哪个直角三角形中看了, 这是不是一个直角三角形?我们分析一下,肯定是直角三角形的吗?其实后边的话,他这个平面你看看好了啊, bc 是不是垂直的?是啊,垂直于 cce 啊,所以后边这样一个平面,他其实是一个矩形的, 对吧?这个很容易得嘛,根据九十度,根据垂直就可以得出来矩形。矩形的话来看,是不是需要先求一下 b 一 c 一的长度,再求一下下边?我觉得不用多求了吧,肯定很容易求出来的啊。我们容易得到的是, 其实有一个全等的,谁呢?三角形 a m c, 它是全等于三角形 a e o c e 的,你这个 c e o 的长度等于一点二,是终点吗?它的长度也是一,所以下面这个 c m 的长度, 它是不是就等于这个 c e o 的长度等于一?它都是一啊,所以我这个 c e m 的长度就等于一加一加一等于三就算出来了。关键在于我这个 b 一 c 一是多长? b 一 c 一。好,第二条辅助线看好了啊,第二条辅助线要干嘛呀?要找一个 b e c e 的终点,因为点 o 已经是终点了,点 n 也也是终点那 o n 的长度,哎,能理解吧。看了啊,千万不要着急,这道题首先看好了。 嗯哪呢,我要换一种颜色吧,千万不要混了看。首先, c c e 它是怎么样的?它是垂直于 a e o 的吧。第一问已经解决过了, 并且呢,根据矩形的特性,这个 c c e, 它也是垂直于这个 o n 的吧?你垂直 c c e, 垂直于整个平面里头两条相照直线,它不就垂直于整个平面 a e、 o n 吗? 所以进而就推出来,这个 c c、 e 是垂直于整个平面里头的最后一条线。垂直于谁?垂直于 a e n? 当你求完垂直于 a e n 之后的话,你这个 a、 e、 n 是不是垂直于 b b e? 来看看 看啊,新增那些条件,括号二,增加了个什么条件?他说这个 aae 和 bb 这两条平行线之间距离就是二,那不就是点 ae 到 bbe 的距离,这个 aen 不就是那个距离等于二吗?对吧?根据已知条件,这个 a、 e、 n 的长度,根据垂直,他就是两个平行线 a a 一和 b b 的距离等于二。好了,剩下呢,不用多说了吧,所以能算了啊。好,我把剩下的东西呢,该擦的都擦掉来。 a e o 等于多少吧?等于一吧。然后呢,这个 a e n 等于多少?等于二吧。那你说这个 o n 等于多长呢? o n 肯定是等于二的平方减去一的平方。勾股定理啊,它是等于根号三的, o n 等于根号三,所以说 b 一 c 一其实也是根号三,所以 记得很清楚啦, b e m, 它的长度是等于根号下 b e c e 的平方,再加上 c e m 的平方, b e c e 的话,平方就是三,这个 c e、 m 的平方就是九,对吧?三的平方等于九,等于根号十二二倍根号三呀。 那么我们要算的最终的结论不是就有了吗?刚才在这样一个位置我已经写过了这个三角 a b e m, 它是等于谁比上谁的,它就是等于这样一个直角边 a m 比上斜边 a b 一的其实也好算啊。那 a m 的话就是一它的平方啊。根据勾股定理,这个 a b 一,它是等于 a m 的平方,其实就是一的平方,再加上谁再加上这个 b e m 的平方吧。那显示等 等于十二点,最终结果就是根号下一加十二,根号十三分之一,也就是说十三分之根号十三就解决完了。所以这道题的话,其实我主推的方法是什么?就是几何的方法。当然,如果你真的要用间隙的方法也能算啊。也不是说不能算,那么真正 聪明的同学是立体几何,间隙的方法也得掌握。还有立体几何纯几何的方法也得掌握清楚了吧。分享课堂知识,感受数学之美。我是安分老师,下节课再见!
4275会放羊的教书匠 04:10查看AI文稿AI文稿
04:10查看AI文稿AI文稿大家好,今天我们一起来看一下二零二二年全国甲醛的第三十四集。第一问,一,平面剪斜横拨以速度 v 等于二米每秒,沿 x 轴正方向传播, t 等于零,时刻播信,图如图所示, 戒指中平衡位置在坐标远点的致点 a 在 t 等于零,时刻位于五二零根号二厘米,让我们求波长频率以及二秒十 a 的运动方向。那看到这个图呢?我们可以写一下他的函数关系, 我们直接去写出 y 就等于正服是二,所以是二倍的三,二派比上 m 的 x 加上二零,那我们知道两个点,第一个点零, k 号二,第二 二点一点五,零零带过来二倍的三分零就等于更好,所以我们知道三分零,二分之高二,那么分零就是 轮着派,我们另外一点五零带过来二倍的三,三派比上难的再加上快,零就等于零, 所以难不大分之三派再加上费林就等于派。让我们把费林带过来, 三派比上难不倒就等于四分之三派,所以难不倒就等于四米。哎呦, 也可能会问了,这里从数学角度来看,这个范玲和我们这边爱这个地方不都是可以取周期性的吗?那为什么我们这边只取了 这样一个唯一的这个结果呢?那么这个图其实我们可以简单看一下,他是不是可以认为是我虚线画的这个地方平移过去的, 那对应的我们这个一点五是不是也可以由右面这个圈过去的?那么同样我们可以看到平移的过程是不是只平移了小于了四分之一的波长, 所以我们这边四分之派和派是这样得来的,那么算到南不大等于四米之后呢?要算频率我们可以先算一下他的周期,周期的等于南不大比上国宿, 那么直接算四比上速度是二,那就是两秒,频率就等于六七分之一,所以就是零点五个子 好波长就是四米,频率是零点五赫兹。接下来我们看最后问我们两秒时刻,那两秒时刻我们刚刚算到周期是不是两秒,所以其实相当于就是问我们零时刻,也就是涂上这个位置之后, 热点 a 他的运动方向,那我们要看他的运动方向,其实最简单的做法就是画一下在传播方向后面一个微小时刻,他的模型, 他是沿正方向传播的,所以这个点我们画出来他传播方向后面的这 一个波形图,他是不是在往下运动的,所以我们就知道这点 a 是向下运动。好,这道题目墙角这一栏就结束了,我们一起来回顾一下这道题目主要考察我们的是 剪些横波,他的波形图,那么我们只要能够写出他的函数关系式, 根据题目中以致的两点代入,就能够把波长算出来。那波长有了之后呢?利用波长速度和周期的这个关系,求出周期,进而求出明率。那最后判断制点运动方向,其实我们就是在 按播方向上平移一小段,那么就能够很容易看出这个质检此刻的运动方向是什么。好,今天的分享就到这里,谢谢大家。
10高中物理-张恒睿










